10.3频率与概率-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册学案Word
文档属性
| 名称 | 10.3频率与概率-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册学案Word |

|
|
| 格式 | docx | ||
| 文件大小 | 101.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 19:11:59 | ||
图片预览


文档简介
①、了解用样本平均数估计总体平均数
③、掌握全面调查与抽样调查
③、理解分层抽样的步骤
一、频率与概率
在大量重复的试验过程中,一个事件发生的频率会很接近于这个事件发生的概率,而且,试验的次数越多,频率与概率之间差距很小的可能性越大
用频率估计概率:大量试验表妹,在任何次数的随机试验候总,一个随机事件A发生的频率具有随机性,一般的,随着试验次数n的增大,频率偏离概率的幅度会缩小,即事件A发生的频率会逐渐稳定于事件A发生的概率P(A),我们称概率的这个性质为频率的稳定性,因此,我们可以用频率估计概率P(A)
二、频率的稳定性
一般地,随着试验次数n的增大,频率偏离概率的幅度会缩小,即事件A发生的频率fn(A)会逐渐稳定于事件A发生的概率P(A).我们称频率的这个性质为频率的稳定性.因此,我们可以用频率fn(A)估计概率P(A).
1.近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,先随机抽取了该市三类垃圾箱总计1000吨生活垃圾,数据统计如下(单位:吨);
“厨余垃圾”箱
“可回收物”箱
“其他垃圾”箱
厨余垃圾
400
100
100
可回收物
30
240
30
其他垃圾
20
20
60
(1)试估计厨余垃圾投放正确的概率;
(2)试估计生活垃圾投放错误的概率;
(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最大时,写出a,b,c的值(结论不要求证明),并求此时s2的值.
(求:S2=
?[
+
+…+
],其中
为数据x1
,
x2
,
…,xn的平均数)
【答案】
(1)解:由题意可知:厨余垃圾600吨,投放到“厨余垃圾”箱400吨,故厨余垃圾投放正确的概率为
(2)解:由题意可知:生活垃圾投放错误有200+60+20+20=300,故生活垃圾投放错误的概率为
(3)解:由题意可知:∵a+b+c=600,∴a,b,c的平均数为200
∴
=
,
∵(a+b+c)2=a2+b2+c2+2ab+2bc+2ac≥a2+b2+c2
,
因此有当a=600,b=0,c=0时,有s2=80000
【考点】极差、方差与标准差,模拟方法估计概率
【解析】(1)厨余垃圾600吨,投放到“厨余垃圾”箱400吨,故可求厨余垃圾投放正确的概率;(2)生活垃圾投放错误有200+60+20+20=300,故可求生活垃圾投放错误的概率;(3)计算方差可得
=
,因此有当a=600,b=0,c=0时,有s2=80000.
2.试利用随机模拟方法计算曲线y=2x
,
x轴及x=±1所围成的“曲边梯形”的面积.
.【答案】
解:(1)利用计算机分别产生[﹣1,1]和[0,2]上的均匀随机数:a=﹣1+2Rand和b=2Rand,得随机数组(a,b).
(2)统计试验总次数N和落在“曲边梯形”内的点数N1(满足b<2a的点(a,b)数).
(3)计算频率
,
得点落在“曲边梯形”上的概率近似值.
(4)由几何概型得p=
,
所以=
,
于是得到S=
,
这就是“曲边梯形”面积的近似值.
【考点】模拟方法估计概率
【解析】用随机模拟方法计算曲线y=2x
,
x轴及x=±1所围成的“曲边梯形”的面积,分成四个步骤:
(1)利用计算机分别产生[﹣1,1]和[0,2]上的均匀随机数;
(2)统计试验总次数N和落在“曲边梯形”内的点数N1(满足b<2a的点(a,b)数).
(3)计算频率
,
得点落在“曲边梯形”上的概率近似值.(4)由几何概型得出“曲边梯形”面积的近似值.
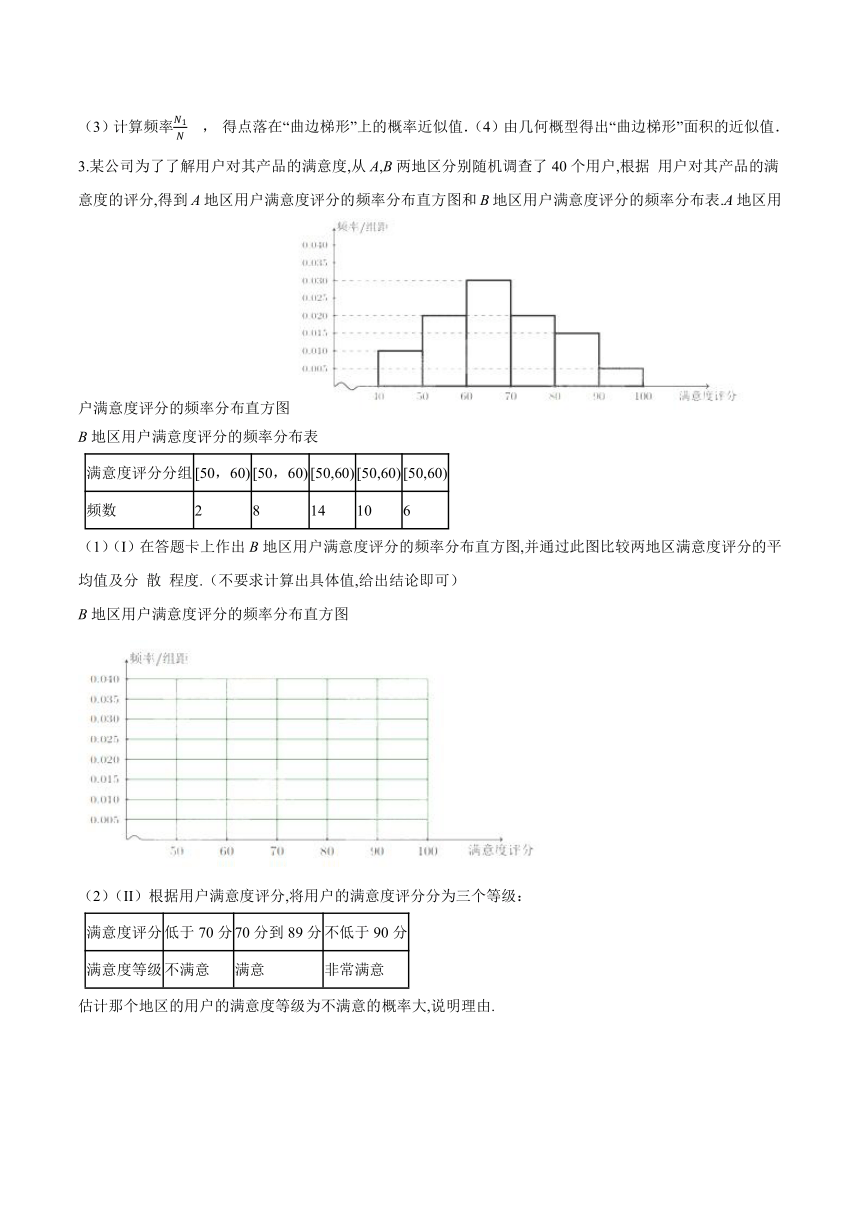
3.某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据
用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.A地区用户满意度评分的频率分布直方图
B地区用户满意度评分的频率分布表
满意度评分分组
[50,60)
[50,60)
[50,60)
[50,60)
[50,60)
频数
2
8
14
10
6
(1)(I)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分
散
程度.(不要求计算出具体值,给出结论即可)
B地区用户满意度评分的频率分布直方图
(2)(II)根据用户满意度评分,将用户的满意度评分分为三个等级:
满意度评分
低于70分
70分到89分
不低于90分
满意度等级
不满意
满意
非常满意
估计那个地区的用户的满意度等级为不满意的概率大,说明理由.
【答案】
(1)
通过两地区用户满意度评分的频率分布直方图可以看出,B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值,B地区用户满意度评分比较集中,A地区用户满意度评分比较分散。
(2)A地区的用户的满意度等级为不满意的概率大.
【考点】频率分布直方图,模拟方法估计概率
【解析】(I)通过两地区用户满意度评分的频率分布直方图可以看出,B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值,B地区用户满意度评分比较集中,而A地区用户满意度评分比较分散
(II)记CA表示事件A地区的用户满意度等级为“不满意”;CB表示事件B地区的用户满意度等级为“不满意”,由直方图得P(CA)的估值为(0.01+0.02+0.03)X10=0.6,P(CB)的估值为(0.005+0.02)X10=0.25
所以A地区的用户的满意度等级为不满意的概率大.
【分析】本题考查主要内容是频率分布直方图及应用,注意在制作频率分布直方图或利用频率分布直方图估计概率时容易出现的一个错误是误将频率当作纵坐标画图错误或估计概率错误,故提醒考生:频率分布直方图中纵坐标是频率/组距,而不是频率.
4.一份测试题包括6道选择题,每题只有一个选项是正确的.如果一个学生对每一道题都随机猜一个答案,用随机模拟方法估计该学生至少答对3道题的概率.
【答案】
解:
我们通过设计模拟试验的方法来解决问题.利用计算机或计算器可以产生0到3之间取整数值的随机数.我们用0表示猜的选项正确,1,2,3表示猜的选项错误,这样可以体现猜对的概率是25%.因为共猜6道题,所以每6个随机数作为一组.例如,产生25组随机数:
330130 302220 133020 022011 313121 222330
231022 001003 213322 030032 100211 022210
231330 321202 031210 232111 210010 212020
230331 112000 102330 200313 303321 012033
321230
就相当于做了25次试验,在每组数中,如果恰有3个或3个以上的数是0,则表示至少答对3道题,它们分别是001003,030032,210010,112000,即共有4组数,我们得到该同学6道选择题至少答对3道题的概率近似为
=0.16.
【考点】模拟方法估计概率
【解析】利用随机模拟方法,估计概率,即可得出答案。
1.如图所示,分别以正方形ABCD两邻边AB、AD为直径向正方形内做两个半圆,交于点O.若向正方形内投掷一颗质地均匀的小球(小球落到每点的可能性均相同),则该球落在阴影部分的概率为(
??)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
2.已知某运动员每次投篮命中的概率都为40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,用1,2,3,4表示命中,用5,6,,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果。经随机模拟产生了20组随机数:
907???
966???
191????
925????
271???
932???
812???
458????
569??
683
431???
257???
393????
027????
556???
488???
730???
113????
537??
989
据此估计,该运动员三次投篮恰有两次命中的概率为?????????????????????
(???
)
A.?0.35?????????????????????????????????????B.?0.30?????????????????????????????????????C.?0.25?????????????????????????????????????D.?0.20
3.某个游戏中,一个珠子按如图所示的通道,由上至下的滑下,从最下面的六个出口出来,规定猜中者为胜,如果你在该游戏中,猜得珠子从口3出来,那么你取胜的概率为(??
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?都不对
4.在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2﹣y=0)的点的个数的估计值为(??
)
A.?5000???????????????????????????????????B.?6667???????????????????????????????????C.?7500???????????????????????????????????D.?7854
参考答案
1.【答案】
C
【解析】
法一:设正方形的边长为2.则这两个半圆的并集所在区域的面积为
,所以该质点落入这两个半圆的并集所在区城内的概率为
.
法二:设正方形的边长为2.过O作OF垂直于AB
,
OE垂直于AD.则这两个半圆的并集所在区域的面积为
,所以该质点落入这两个半圆的并集所在区域的概率为
,
2.【答案】
C
【解析】
由题意知模拟三次投篮的结果,经随机模拟产生了如下20组随机数,在20组随机数中表示三次投篮恰有两次命中的有可以通过列举得到共5组随机数,根据概率公式,得到结果.
由题意知模拟三次投篮的结果,经随机模拟产生了如下20组随机数,
在20组随机数中表示三次投篮恰有两次命中的有:191、271、932、812、393.
共5组随机数,
∴所求概率为==0.25.
故选C.
3.【答案】
A
【解析】
所求的概率为
?,故选A.
分析可得从A到3总共有5个岔口,每一岔口走法的概率都是,而从A到3总共有C52=10种走法,计算可得答案.
4.【答案】B
【解析】
解:由题意,阴影部分的面积S=
=
=
,正方形的面积为1,
∵正方形中随机投掷10000个点,
∴落入阴影部分(曲线C的方程为x2﹣y=0)的点的个数的估计值为10000×
≈6667,
故选B.
③、掌握全面调查与抽样调查
③、理解分层抽样的步骤
一、频率与概率
在大量重复的试验过程中,一个事件发生的频率会很接近于这个事件发生的概率,而且,试验的次数越多,频率与概率之间差距很小的可能性越大
用频率估计概率:大量试验表妹,在任何次数的随机试验候总,一个随机事件A发生的频率具有随机性,一般的,随着试验次数n的增大,频率偏离概率的幅度会缩小,即事件A发生的频率会逐渐稳定于事件A发生的概率P(A),我们称概率的这个性质为频率的稳定性,因此,我们可以用频率估计概率P(A)
二、频率的稳定性
一般地,随着试验次数n的增大,频率偏离概率的幅度会缩小,即事件A发生的频率fn(A)会逐渐稳定于事件A发生的概率P(A).我们称频率的这个性质为频率的稳定性.因此,我们可以用频率fn(A)估计概率P(A).
1.近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,先随机抽取了该市三类垃圾箱总计1000吨生活垃圾,数据统计如下(单位:吨);
“厨余垃圾”箱
“可回收物”箱
“其他垃圾”箱
厨余垃圾
400
100
100
可回收物
30
240
30
其他垃圾
20
20
60
(1)试估计厨余垃圾投放正确的概率;
(2)试估计生活垃圾投放错误的概率;
(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最大时,写出a,b,c的值(结论不要求证明),并求此时s2的值.
(求:S2=
?[
+
+…+
],其中
为数据x1
,
x2
,
…,xn的平均数)
【答案】
(1)解:由题意可知:厨余垃圾600吨,投放到“厨余垃圾”箱400吨,故厨余垃圾投放正确的概率为
(2)解:由题意可知:生活垃圾投放错误有200+60+20+20=300,故生活垃圾投放错误的概率为
(3)解:由题意可知:∵a+b+c=600,∴a,b,c的平均数为200
∴
=
,
∵(a+b+c)2=a2+b2+c2+2ab+2bc+2ac≥a2+b2+c2
,
因此有当a=600,b=0,c=0时,有s2=80000
【考点】极差、方差与标准差,模拟方法估计概率
【解析】(1)厨余垃圾600吨,投放到“厨余垃圾”箱400吨,故可求厨余垃圾投放正确的概率;(2)生活垃圾投放错误有200+60+20+20=300,故可求生活垃圾投放错误的概率;(3)计算方差可得
=
,因此有当a=600,b=0,c=0时,有s2=80000.
2.试利用随机模拟方法计算曲线y=2x
,
x轴及x=±1所围成的“曲边梯形”的面积.
.【答案】
解:(1)利用计算机分别产生[﹣1,1]和[0,2]上的均匀随机数:a=﹣1+2Rand和b=2Rand,得随机数组(a,b).
(2)统计试验总次数N和落在“曲边梯形”内的点数N1(满足b<2a的点(a,b)数).
(3)计算频率
,
得点落在“曲边梯形”上的概率近似值.
(4)由几何概型得p=
,
所以=
,
于是得到S=
,
这就是“曲边梯形”面积的近似值.
【考点】模拟方法估计概率
【解析】用随机模拟方法计算曲线y=2x
,
x轴及x=±1所围成的“曲边梯形”的面积,分成四个步骤:
(1)利用计算机分别产生[﹣1,1]和[0,2]上的均匀随机数;
(2)统计试验总次数N和落在“曲边梯形”内的点数N1(满足b<2a的点(a,b)数).
(3)计算频率
,
得点落在“曲边梯形”上的概率近似值.(4)由几何概型得出“曲边梯形”面积的近似值.
3.某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据
用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.A地区用户满意度评分的频率分布直方图
B地区用户满意度评分的频率分布表
满意度评分分组
[50,60)
[50,60)
[50,60)
[50,60)
[50,60)
频数
2
8
14
10
6
(1)(I)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分
散
程度.(不要求计算出具体值,给出结论即可)
B地区用户满意度评分的频率分布直方图
(2)(II)根据用户满意度评分,将用户的满意度评分分为三个等级:
满意度评分
低于70分
70分到89分
不低于90分
满意度等级
不满意
满意
非常满意
估计那个地区的用户的满意度等级为不满意的概率大,说明理由.
【答案】
(1)
通过两地区用户满意度评分的频率分布直方图可以看出,B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值,B地区用户满意度评分比较集中,A地区用户满意度评分比较分散。
(2)A地区的用户的满意度等级为不满意的概率大.
【考点】频率分布直方图,模拟方法估计概率
【解析】(I)通过两地区用户满意度评分的频率分布直方图可以看出,B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值,B地区用户满意度评分比较集中,而A地区用户满意度评分比较分散
(II)记CA表示事件A地区的用户满意度等级为“不满意”;CB表示事件B地区的用户满意度等级为“不满意”,由直方图得P(CA)的估值为(0.01+0.02+0.03)X10=0.6,P(CB)的估值为(0.005+0.02)X10=0.25
所以A地区的用户的满意度等级为不满意的概率大.
【分析】本题考查主要内容是频率分布直方图及应用,注意在制作频率分布直方图或利用频率分布直方图估计概率时容易出现的一个错误是误将频率当作纵坐标画图错误或估计概率错误,故提醒考生:频率分布直方图中纵坐标是频率/组距,而不是频率.
4.一份测试题包括6道选择题,每题只有一个选项是正确的.如果一个学生对每一道题都随机猜一个答案,用随机模拟方法估计该学生至少答对3道题的概率.
【答案】
解:
我们通过设计模拟试验的方法来解决问题.利用计算机或计算器可以产生0到3之间取整数值的随机数.我们用0表示猜的选项正确,1,2,3表示猜的选项错误,这样可以体现猜对的概率是25%.因为共猜6道题,所以每6个随机数作为一组.例如,产生25组随机数:
330130 302220 133020 022011 313121 222330
231022 001003 213322 030032 100211 022210
231330 321202 031210 232111 210010 212020
230331 112000 102330 200313 303321 012033
321230
就相当于做了25次试验,在每组数中,如果恰有3个或3个以上的数是0,则表示至少答对3道题,它们分别是001003,030032,210010,112000,即共有4组数,我们得到该同学6道选择题至少答对3道题的概率近似为
=0.16.
【考点】模拟方法估计概率
【解析】利用随机模拟方法,估计概率,即可得出答案。
1.如图所示,分别以正方形ABCD两邻边AB、AD为直径向正方形内做两个半圆,交于点O.若向正方形内投掷一颗质地均匀的小球(小球落到每点的可能性均相同),则该球落在阴影部分的概率为(
??)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
2.已知某运动员每次投篮命中的概率都为40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,用1,2,3,4表示命中,用5,6,,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果。经随机模拟产生了20组随机数:
907???
966???
191????
925????
271???
932???
812???
458????
569??
683
431???
257???
393????
027????
556???
488???
730???
113????
537??
989
据此估计,该运动员三次投篮恰有两次命中的概率为?????????????????????
(???
)
A.?0.35?????????????????????????????????????B.?0.30?????????????????????????????????????C.?0.25?????????????????????????????????????D.?0.20
3.某个游戏中,一个珠子按如图所示的通道,由上至下的滑下,从最下面的六个出口出来,规定猜中者为胜,如果你在该游戏中,猜得珠子从口3出来,那么你取胜的概率为(??
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?都不对
4.在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2﹣y=0)的点的个数的估计值为(??
)
A.?5000???????????????????????????????????B.?6667???????????????????????????????????C.?7500???????????????????????????????????D.?7854
参考答案
1.【答案】
C
【解析】
法一:设正方形的边长为2.则这两个半圆的并集所在区域的面积为
,所以该质点落入这两个半圆的并集所在区城内的概率为
.
法二:设正方形的边长为2.过O作OF垂直于AB
,
OE垂直于AD.则这两个半圆的并集所在区域的面积为
,所以该质点落入这两个半圆的并集所在区域的概率为
,
2.【答案】
C
【解析】
由题意知模拟三次投篮的结果,经随机模拟产生了如下20组随机数,在20组随机数中表示三次投篮恰有两次命中的有可以通过列举得到共5组随机数,根据概率公式,得到结果.
由题意知模拟三次投篮的结果,经随机模拟产生了如下20组随机数,
在20组随机数中表示三次投篮恰有两次命中的有:191、271、932、812、393.
共5组随机数,
∴所求概率为==0.25.
故选C.
3.【答案】
A
【解析】
所求的概率为
?,故选A.
分析可得从A到3总共有5个岔口,每一岔口走法的概率都是,而从A到3总共有C52=10种走法,计算可得答案.
4.【答案】B
【解析】
解:由题意,阴影部分的面积S=
=
=
,正方形的面积为1,
∵正方形中随机投掷10000个点,
∴落入阴影部分(曲线C的方程为x2﹣y=0)的点的个数的估计值为10000×
≈6667,
故选B.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
