9.2.3总体集中趋势的估计、9.2.4总体离散程度的估计-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册复习巩固训练Word含答案
文档属性
| 名称 | 9.2.3总体集中趋势的估计、9.2.4总体离散程度的估计-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册复习巩固训练Word含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 181.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 00:00:00 | ||
图片预览



文档简介
9.2.3总体集中趋势的估计 9.2.4总体离散程度的估计
一、知识梳理
1. 总体集中趋势的估计
⑴众数:在频率分布直方图中,众数的估计值是_____________________。
⑵中位数:在频率分布直方图中,众数的估计值是画一条与横轴垂直的直线,使得直方图在直线左右两边的________,该直线与横轴交点的横坐标。
⑶平均数:在频率分布直方图中,样本的平均数可以用每个小矩形底边中点的_______与小矩形的面积的____之和近似代替。
2.总体离散程度的估计
⑴方差、标准差的定义:如果一个样本中个体的变量值分别为样本平均数为,则称为样本方差,为样本标准差。
⑵方差、标准差的结论:若一个样本中个体的变量值的平均数、方差、标准差分别为,则的平均数、方差、标准差分别为________,
_________,____________.
二、重要题型
知识点一 :平均数、中位数、众数的计算
1.某学习小组在一次数学测验中,得100分的有1人,95分的有1人,90分的有2人,85分的有4人,80分和75分的各有1人,则该小组成绩的平均数、众数、中位数分别是( )
A.85,85,85 B.87,85,86
C.87,85,85 D.87,85,90
2.某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组,绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.
求:(1)高一参赛学生的成绩的众数、中位数;
(2)高一参赛学生的平均成绩.
知识点二 :平均数、中位数、众数的实际应用
3.某公司销售部有销售人员15人,为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位销售人员该月销售量的平均数、中位数及众数;
(2)假设销售部负责人把每位销售人员的月销售定额定为320件,你认为是否合理,为什么?如果不合理,请你制定一个较合理的销售定额.
知识点三:样本的标准差、方差的计算
4.在某项体育比赛中,七位裁判为一选手打出的分数如下:90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
A.92,2 B.92,2.8 C.93,2 D.93,2.8
5.现有10个数,其平均数为3,且这10个数的平方和是100,那么这组数据的标准差是( )
A.1 B.2 C.3 D.4
6.一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
A.57.2,3.6 B.57.2,56.4
C.62.8,63.6 D.62.8,3.6
知识点四:样本的标准差、方差的实际应用
7.甲、乙两名战士在相同条件下各打靶10次,每次命中的环数分别是:
甲:8,6,7,8,6,5,9,10,4,7;乙:6,7,7,8,6,7,8,7,9,5.
(1)分别计算以上两组数据的平均数;
(2)分别求出两组数据的方差;
(3)根据计算结果,估计两名战士的射击情况.若要从这两人中选一人参加射击比赛,选谁去合适?
(4)甲、乙两名战士的成绩在[-2s,+2s]内有多少?
三、巩固练习
1.在某次考试中,10名同学的得分如下:84,77,84,83,68,78,70,85,79,95.则这一组数据的众数、中位数和75%分位数分别为( )
A.84,68,83 B.84,78,83
C.84,81,84 D.78,81,84
2.对某小区100户居民的月均用水量进行统计,得到样本的频率分布直方图如图所示,则估计此样本的众数、中位数分别为( )
A.2.25,2.5 B.2.25,2.02
C.2,2.5 D.2.5,2.25
3.从某项综合能力测试中抽取100人的成绩,统计如下表,则这100人的成绩的标准差为( )
分数 5 4 3 2 1
人数 20 10 30 30 10
A. B. C.3 D.
4.一组数据的平均值是,标准差是s,将这组数据中的每个数据都乘以2,所得到的一组新数据的平均值和标准差分别是( )
A.,s B.,2s C.2,s D.2,2s
5.近年来,某市私家车数量持续增长,2015年至2019年该市私家车数量依次为15,19,22,26,30(单位:万辆),则该组数据的中位数是________,10%分位数是________,20%分位数是________.
6.某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x-y|的值为________.
7.某班有50名学生,其中有30名男生和20名女生,随机询问了该班6名男生和4名女生在某次数学测验中的成绩,6名男生的成绩分别为86分,94分,88分,92分,90分,90分,4名女生的成绩分别为90分,93分,93分,88分,则下列说法:
①这种抽样方法是比例分配的分层随机抽样;
②该班男生成绩的平均数小于该班女生成绩的平均数;
③这6名男生成绩的方差大于这4名女生成绩的方差;
④被抽取的10名学生成绩的平均数和方差分别为90.4分和6.04.
其中一定正确的是________(写出所有正确说法的序号).
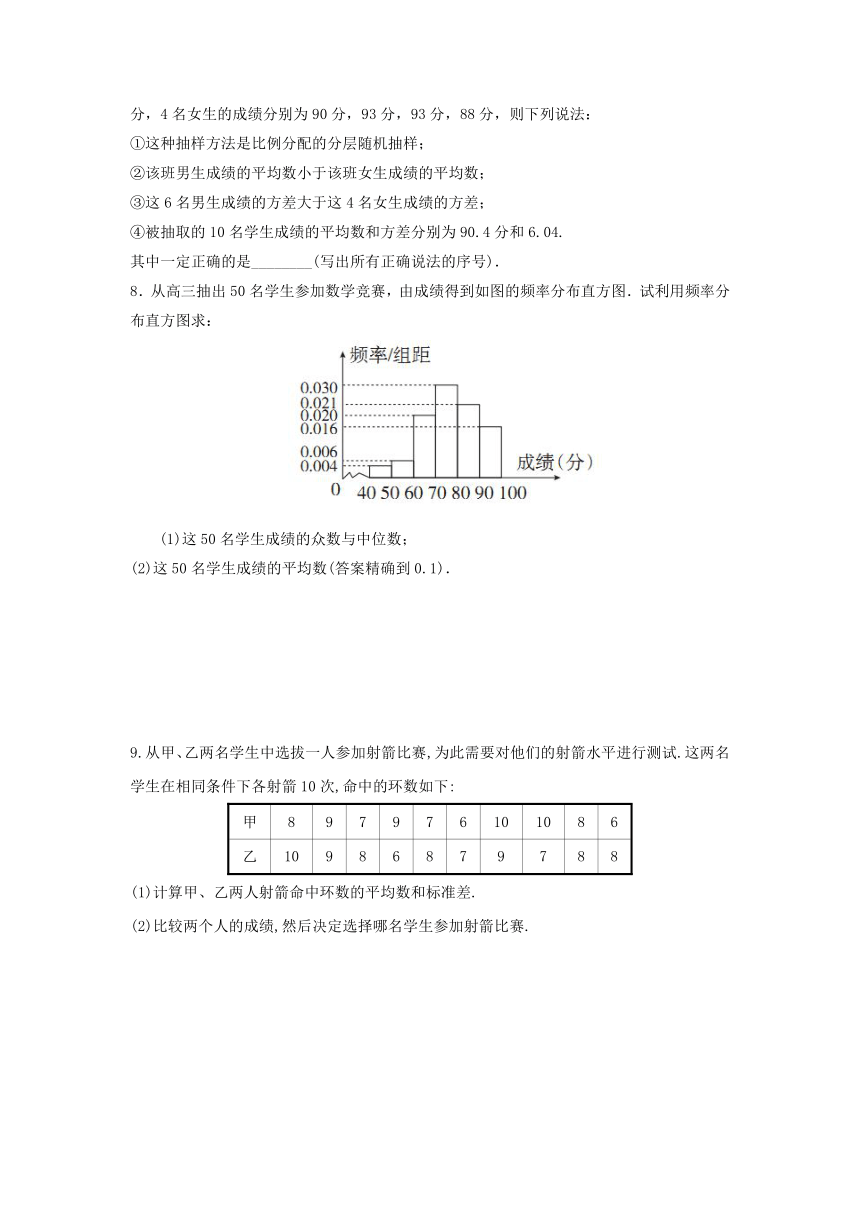
8.从高三抽出50名学生参加数学竞赛,由成绩得到如图的频率分布直方图.试利用频率分布直方图求:
(1)这50名学生成绩的众数与中位数;
(2)这50名学生成绩的平均数(答案精确到0.1).
9.从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 8 9 7 9 7 6 10 10 8 6
乙 10 9 8 6 8 7 9 7 8 8
(1)计算甲、乙两人射箭命中环数的平均数和标准差.
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
9.2.3总体集中趋势的估计 9.2.4总体离散程度的估计
参考答案
一、知识梳理
1. ⑴最高矩形底边中点的横坐标。⑵面积相等.⑶横坐标, 乘积.
2. ⑴或,。⑵.
二、重要题型
1.C 由平均数、中位数、众数的定义可知,平均数
==87;因为得85分的有4人,所以众数是85;把成绩由大到小排列为100,95,90,90,85,85,85,85,80,75,故中位数是85.
2.解:(1)由图可知众数为65,因为第一个小矩形的面积为0.3,所以设中位数为60+x,则0.3+x×0.04=0.5,得x=5,所以中位数为60+5=65.
(2)依题意,平均成绩为55×0.3+65×0.4+75×0.15+85×0.1+95×0.05=67,故平均成绩约为67.
3.解:(1)平均数=×(1800×1+510×1+250×3+210×5+150×3+120×2)=320,
中位数为210,众数为210.
(2)不合理.因为15人中有13人的销售额达不到320件,也就是说,320虽是这一组数据的平均数,但它却不能反映销售人员的一般水平.销售额定为210件合理些,这是由于210既是中位数,又是众数,是绝大部分人都能达到的销售额.
4.B 去掉一个最高分95与一个最低分89后,所得的5个数分别为90,90,93,94,93,
所以===92,s2==
=2.8,故选B.
5.A 由s2=- 2,得s2=×100-32=1,即标准差s=1.
6.D 每一个数据都加上60,所得新数据的平均数增加60,而方差保持不变.
7.解:(1)甲=×(8+6+7+8+6+5+9+10+4+7)=7,
乙=×(6+7+7+8+6+7+8+7+9+5)=7.
(2)由方差公式s2=(xi-)2,得s=3,s=1.2.
(3)甲=乙,说明甲、乙两战士的平均水平相当.又s>s,说明甲战士射击情况波动比乙大.因此,乙战士比甲战士射击情况稳定.从成绩的稳定性考虑,应选择乙参加比赛.
(4)因为s甲==≈1.73,甲-2s甲≈3.54,甲+2s甲≈10.46,所以甲战士的成绩全部在[-2s,+2s]内.因为s乙==≈1.10,乙-2s乙≈4.8,
乙+2s乙≈9.2,所以乙战士的成绩也全部在[-2s,+2s]内.
三、巩固练习
1.C 将所给数据按从小到大的顺序排列是68,70,77,78,79,83,84,84,85,95,显然众数为84,而本组数据共10个,中间两个数是79,83,它们的平均数为81,即中位数为81.因为10×75%=7.5,所以这一组数据的75%分位数为84.故选C.
2.B 众数是指样本中出现频率最高的数,在频率分布直方图中通常取该组区间的中点,所以众数为=2.25.中位数是频率为0.5的分界点,由频率分布直方图,可知前4组的频率和为(0.08+0.16+0.30+0.44)×0.5=0.49,因此中位数出现在第5组,设中位数为x,则(x-2)×0.5=0.01,解得x=2.02,故选B.
3.B 平均数为=3.
故s2=×[20×(5-3)2+10×(4-3)2+30×(3-3)2+30×(2-3)2+10×(1-3)2]=.
故s==.
4.D 设该组数据为x1,x2,…,xn,都乘以2后的新数据为2x1,2x2,…,2xn.
由题意知=,则=2.
又s= ,
所以 =2s.故选D.
5.22 15 17 这组数据从小到大排列后,22处于最中间的位置,故这组数据的中位数是22.∵5×10%=0.5,∴该组数据的10%分位数是15,∵5×20%=1,∴该组数据的20%分位数是=17.
6.4 由题意可得x+y=20,(x-10)2+(y-10)2=8,设x=10+t,y=10-t,则t2=4,
|t|=2,故|x-y|=2|t|=4.
7.①③④ 因为该班有30名男生和20名女生且抽取的男生和女生的比为3∶2,所以这种抽样方法是比例分配的分层随机抽样,①正确;抽取的6名男生成绩的平均数
男==90(分),抽取的4名女生成绩的平均数女==91(分),虽然男<女,但并不一定能说明该班男生成绩的平均数小于该班女生成绩的平均数,②不一定正确;这6名男生成绩的方差s=×[(86-90)2+(94-90)2+(88-90)2+(92-90)2+(90-90)2+(90-90)2]=,这4名女生成绩的方差s=×[(90-91)2+(93-91)2+(93-91)2+(88-91)2]=,因为>,所以③正确;被抽取的10名学生成绩的平均数=×90+×91=90.4(分),被抽取的10名学生成绩的方差s2=×+×=4.096+1.944=6.04,④正确.故一定正确的是①③④.
8.解:(1)由众数的概念可知,众数是出现次数最多的数.在直方图中高度最高的小长方形框的中间值的横坐标即为所求,所以由频率分布直方图得众数应为75.
由于中位数是所有数据中的中间值,故在频率分布直方图中体现的是中位数的左右两边频数应相等,即频率也相等,从而就是小矩形的面积和相等.因此在频率分布直方图中将频率分布直方图中所有小矩形的面积一分为二的直线所对应的成绩即为所求.
∵0.004×10+0.006×10+0.02×10=0.04+0.06+0.2=0.3,
∴前三个小矩形面积的和为0.3,而第四个小矩形面积为0.03×10=0.3,0.3+0.3>0.5,
∴中位数应位于第四个小矩形内.设其底边为x,高为0.03,令0.03x=0.2得x≈6.7,
故中位数约为70+6.7=76.7.
(2)样本平均值应是所有数据的平均值,取每个小矩形底边的中点值乘以每个小矩形的面积即可.∴平均数为45×(0.004×10)+55×(0.006×10)+65×(0.02×10)+75×(0.03×10)+85×(0.021×10)+95×(0.016×10)≈73.7.
9.解:(1)根据题中所给数据,可得甲的平均数为,
乙的平均数为,
甲的标准差为,
乙的标准差为。
故甲的平均数为8,标准差为,乙的平均数为8,标准差为.
(2)因为,且,所以乙的成绩较为稳定,故选择乙参加射箭比赛.
一、知识梳理
1. 总体集中趋势的估计
⑴众数:在频率分布直方图中,众数的估计值是_____________________。
⑵中位数:在频率分布直方图中,众数的估计值是画一条与横轴垂直的直线,使得直方图在直线左右两边的________,该直线与横轴交点的横坐标。
⑶平均数:在频率分布直方图中,样本的平均数可以用每个小矩形底边中点的_______与小矩形的面积的____之和近似代替。
2.总体离散程度的估计
⑴方差、标准差的定义:如果一个样本中个体的变量值分别为样本平均数为,则称为样本方差,为样本标准差。
⑵方差、标准差的结论:若一个样本中个体的变量值的平均数、方差、标准差分别为,则的平均数、方差、标准差分别为________,
_________,____________.
二、重要题型
知识点一 :平均数、中位数、众数的计算
1.某学习小组在一次数学测验中,得100分的有1人,95分的有1人,90分的有2人,85分的有4人,80分和75分的各有1人,则该小组成绩的平均数、众数、中位数分别是( )
A.85,85,85 B.87,85,86
C.87,85,85 D.87,85,90
2.某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组,绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.
求:(1)高一参赛学生的成绩的众数、中位数;
(2)高一参赛学生的平均成绩.
知识点二 :平均数、中位数、众数的实际应用
3.某公司销售部有销售人员15人,为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位销售人员该月销售量的平均数、中位数及众数;
(2)假设销售部负责人把每位销售人员的月销售定额定为320件,你认为是否合理,为什么?如果不合理,请你制定一个较合理的销售定额.
知识点三:样本的标准差、方差的计算
4.在某项体育比赛中,七位裁判为一选手打出的分数如下:90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
A.92,2 B.92,2.8 C.93,2 D.93,2.8
5.现有10个数,其平均数为3,且这10个数的平方和是100,那么这组数据的标准差是( )
A.1 B.2 C.3 D.4
6.一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
A.57.2,3.6 B.57.2,56.4
C.62.8,63.6 D.62.8,3.6
知识点四:样本的标准差、方差的实际应用
7.甲、乙两名战士在相同条件下各打靶10次,每次命中的环数分别是:
甲:8,6,7,8,6,5,9,10,4,7;乙:6,7,7,8,6,7,8,7,9,5.
(1)分别计算以上两组数据的平均数;
(2)分别求出两组数据的方差;
(3)根据计算结果,估计两名战士的射击情况.若要从这两人中选一人参加射击比赛,选谁去合适?
(4)甲、乙两名战士的成绩在[-2s,+2s]内有多少?
三、巩固练习
1.在某次考试中,10名同学的得分如下:84,77,84,83,68,78,70,85,79,95.则这一组数据的众数、中位数和75%分位数分别为( )
A.84,68,83 B.84,78,83
C.84,81,84 D.78,81,84
2.对某小区100户居民的月均用水量进行统计,得到样本的频率分布直方图如图所示,则估计此样本的众数、中位数分别为( )
A.2.25,2.5 B.2.25,2.02
C.2,2.5 D.2.5,2.25
3.从某项综合能力测试中抽取100人的成绩,统计如下表,则这100人的成绩的标准差为( )
分数 5 4 3 2 1
人数 20 10 30 30 10
A. B. C.3 D.
4.一组数据的平均值是,标准差是s,将这组数据中的每个数据都乘以2,所得到的一组新数据的平均值和标准差分别是( )
A.,s B.,2s C.2,s D.2,2s
5.近年来,某市私家车数量持续增长,2015年至2019年该市私家车数量依次为15,19,22,26,30(单位:万辆),则该组数据的中位数是________,10%分位数是________,20%分位数是________.
6.某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x-y|的值为________.
7.某班有50名学生,其中有30名男生和20名女生,随机询问了该班6名男生和4名女生在某次数学测验中的成绩,6名男生的成绩分别为86分,94分,88分,92分,90分,90分,4名女生的成绩分别为90分,93分,93分,88分,则下列说法:
①这种抽样方法是比例分配的分层随机抽样;
②该班男生成绩的平均数小于该班女生成绩的平均数;
③这6名男生成绩的方差大于这4名女生成绩的方差;
④被抽取的10名学生成绩的平均数和方差分别为90.4分和6.04.
其中一定正确的是________(写出所有正确说法的序号).
8.从高三抽出50名学生参加数学竞赛,由成绩得到如图的频率分布直方图.试利用频率分布直方图求:
(1)这50名学生成绩的众数与中位数;
(2)这50名学生成绩的平均数(答案精确到0.1).
9.从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 8 9 7 9 7 6 10 10 8 6
乙 10 9 8 6 8 7 9 7 8 8
(1)计算甲、乙两人射箭命中环数的平均数和标准差.
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
9.2.3总体集中趋势的估计 9.2.4总体离散程度的估计
参考答案
一、知识梳理
1. ⑴最高矩形底边中点的横坐标。⑵面积相等.⑶横坐标, 乘积.
2. ⑴或,。⑵.
二、重要题型
1.C 由平均数、中位数、众数的定义可知,平均数
==87;因为得85分的有4人,所以众数是85;把成绩由大到小排列为100,95,90,90,85,85,85,85,80,75,故中位数是85.
2.解:(1)由图可知众数为65,因为第一个小矩形的面积为0.3,所以设中位数为60+x,则0.3+x×0.04=0.5,得x=5,所以中位数为60+5=65.
(2)依题意,平均成绩为55×0.3+65×0.4+75×0.15+85×0.1+95×0.05=67,故平均成绩约为67.
3.解:(1)平均数=×(1800×1+510×1+250×3+210×5+150×3+120×2)=320,
中位数为210,众数为210.
(2)不合理.因为15人中有13人的销售额达不到320件,也就是说,320虽是这一组数据的平均数,但它却不能反映销售人员的一般水平.销售额定为210件合理些,这是由于210既是中位数,又是众数,是绝大部分人都能达到的销售额.
4.B 去掉一个最高分95与一个最低分89后,所得的5个数分别为90,90,93,94,93,
所以===92,s2==
=2.8,故选B.
5.A 由s2=- 2,得s2=×100-32=1,即标准差s=1.
6.D 每一个数据都加上60,所得新数据的平均数增加60,而方差保持不变.
7.解:(1)甲=×(8+6+7+8+6+5+9+10+4+7)=7,
乙=×(6+7+7+8+6+7+8+7+9+5)=7.
(2)由方差公式s2=(xi-)2,得s=3,s=1.2.
(3)甲=乙,说明甲、乙两战士的平均水平相当.又s>s,说明甲战士射击情况波动比乙大.因此,乙战士比甲战士射击情况稳定.从成绩的稳定性考虑,应选择乙参加比赛.
(4)因为s甲==≈1.73,甲-2s甲≈3.54,甲+2s甲≈10.46,所以甲战士的成绩全部在[-2s,+2s]内.因为s乙==≈1.10,乙-2s乙≈4.8,
乙+2s乙≈9.2,所以乙战士的成绩也全部在[-2s,+2s]内.
三、巩固练习
1.C 将所给数据按从小到大的顺序排列是68,70,77,78,79,83,84,84,85,95,显然众数为84,而本组数据共10个,中间两个数是79,83,它们的平均数为81,即中位数为81.因为10×75%=7.5,所以这一组数据的75%分位数为84.故选C.
2.B 众数是指样本中出现频率最高的数,在频率分布直方图中通常取该组区间的中点,所以众数为=2.25.中位数是频率为0.5的分界点,由频率分布直方图,可知前4组的频率和为(0.08+0.16+0.30+0.44)×0.5=0.49,因此中位数出现在第5组,设中位数为x,则(x-2)×0.5=0.01,解得x=2.02,故选B.
3.B 平均数为=3.
故s2=×[20×(5-3)2+10×(4-3)2+30×(3-3)2+30×(2-3)2+10×(1-3)2]=.
故s==.
4.D 设该组数据为x1,x2,…,xn,都乘以2后的新数据为2x1,2x2,…,2xn.
由题意知=,则=2.
又s= ,
所以 =2s.故选D.
5.22 15 17 这组数据从小到大排列后,22处于最中间的位置,故这组数据的中位数是22.∵5×10%=0.5,∴该组数据的10%分位数是15,∵5×20%=1,∴该组数据的20%分位数是=17.
6.4 由题意可得x+y=20,(x-10)2+(y-10)2=8,设x=10+t,y=10-t,则t2=4,
|t|=2,故|x-y|=2|t|=4.
7.①③④ 因为该班有30名男生和20名女生且抽取的男生和女生的比为3∶2,所以这种抽样方法是比例分配的分层随机抽样,①正确;抽取的6名男生成绩的平均数
男==90(分),抽取的4名女生成绩的平均数女==91(分),虽然男<女,但并不一定能说明该班男生成绩的平均数小于该班女生成绩的平均数,②不一定正确;这6名男生成绩的方差s=×[(86-90)2+(94-90)2+(88-90)2+(92-90)2+(90-90)2+(90-90)2]=,这4名女生成绩的方差s=×[(90-91)2+(93-91)2+(93-91)2+(88-91)2]=,因为>,所以③正确;被抽取的10名学生成绩的平均数=×90+×91=90.4(分),被抽取的10名学生成绩的方差s2=×+×=4.096+1.944=6.04,④正确.故一定正确的是①③④.
8.解:(1)由众数的概念可知,众数是出现次数最多的数.在直方图中高度最高的小长方形框的中间值的横坐标即为所求,所以由频率分布直方图得众数应为75.
由于中位数是所有数据中的中间值,故在频率分布直方图中体现的是中位数的左右两边频数应相等,即频率也相等,从而就是小矩形的面积和相等.因此在频率分布直方图中将频率分布直方图中所有小矩形的面积一分为二的直线所对应的成绩即为所求.
∵0.004×10+0.006×10+0.02×10=0.04+0.06+0.2=0.3,
∴前三个小矩形面积的和为0.3,而第四个小矩形面积为0.03×10=0.3,0.3+0.3>0.5,
∴中位数应位于第四个小矩形内.设其底边为x,高为0.03,令0.03x=0.2得x≈6.7,
故中位数约为70+6.7=76.7.
(2)样本平均值应是所有数据的平均值,取每个小矩形底边的中点值乘以每个小矩形的面积即可.∴平均数为45×(0.004×10)+55×(0.006×10)+65×(0.02×10)+75×(0.03×10)+85×(0.021×10)+95×(0.016×10)≈73.7.
9.解:(1)根据题中所给数据,可得甲的平均数为,
乙的平均数为,
甲的标准差为,
乙的标准差为。
故甲的平均数为8,标准差为,乙的平均数为8,标准差为.
(2)因为,且,所以乙的成绩较为稳定,故选择乙参加射箭比赛.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
