10.2事件的相互独立性-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册复习巩固训练Word含答案
文档属性
| 名称 | 10.2事件的相互独立性-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册复习巩固训练Word含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 181.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 19:15:25 | ||
图片预览



文档简介
10.2 事件的相互独立性
一、知识梳理
1.相互独立事件:对于两个事件A与B,如果____________成立,则称事件A与事件B相互独立。
2. 相互独立事件的结论:如果事件A与事件B相互独立,那么A与,与B,与都_____。
二、重要题型
知识点一:事件独立性的判定
1.一个家庭中有若干个小孩,假定生男孩和生女孩是等可能的,令A={一个家庭中既有男孩又有女孩},B={一个家庭中最多有一个女孩}.对下述两种情形,讨论A与B的独立性:
(1)家庭中有两个小孩;
(2)家庭中有三个小孩.
知识点二:相互独立事件同时发生的概率
2.某人提出一个问题,甲先答,答对的概率为0.4,如果甲答错,由乙答,答对的概率为0.5,则问题由乙答对的概率为( )
A.0.2 B.0.8 C.0.4 D.0.3
3.若三个原件A,B,C按照如图的方式连接成一个系统,每个原件是否正常工作不受其他元件的影响,当原件A正常工作且B,C中至少有一个正常工作时,系统就正常工作,若原件A,B,C正常工作的概率依次为0.7,0.8,0.9,则这个系统正常工作的概率为
知识点三:相互独立事件的综合应用
4.有一道数学难题,学生A解出的概率为,学生B解出的概率为,学生C解出的概率为.若A,B,C三人独立去解答此题,则恰有一人解出的概率为( )
A.1 B. C. D.
5.某中学根据学生的兴趣爱好,分别创建了“书法”、“诗词”、“理学”三个社团,据资料统计新生通过考核选拔进入这三个社团成功与否相互独立.2015年某新生入学,假设他通过考核选拔进入该校的“书法”、“诗词”、“理学”三个社团的概率依次为m、、n,已知三个社团他都能进入的概率为,至少进入一个社团的概率为,且m>n.
(l)求m与n的值;
(2)该校根据三个社团活动安排情况,对进入“书法”社的同学增加校本选修学分1分,对进入“诗词”社的同学增加校本选修学分2分,对进入“理学”社的同学增加校本选修学分3分.求该新同学在社团方面获得校本选修课学分分数不低于4分的概率.
三、巩固练习
1.掷一枚骰子一次,记A表示事件“出现偶数点”,B表示事件“出现3点或6点”,则事件A与B的关系是( )
A.互斥事件 B.相互独立事件
C.既互斥又相互独立事件 D.既不互斥又不相互独立事件
2.甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为和,则两人合作译出密码的概率为( )
A. B. C. D.
3.设两个独立事件A和B都不发生的概率为,A发生B不发生的概率与B发生A不发生的概率相同,则事件A发生的概率P(A)是( )
A. B. C. D.
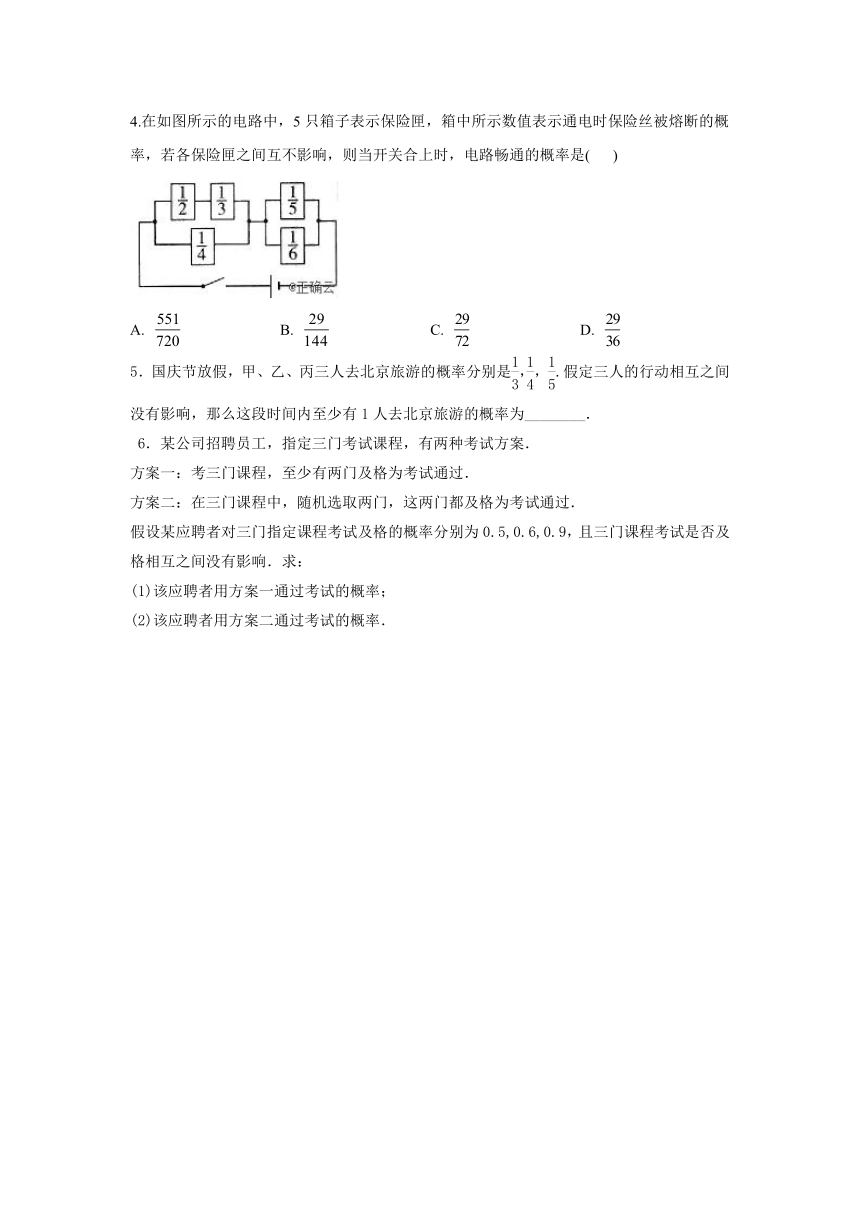
4.在如图所示的电路中,5只箱子表示保险匣,箱中所示数值表示通电时保险丝被熔断的概率,若各保险匣之间互不影响,则当开关合上时,电路畅通的概率是( )
A. B. C. D.
5.国庆节放假,甲、乙、丙三人去北京旅游的概率分别是,,.假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为________.
6.某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考三门课程,至少有两门及格为考试通过.
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别为0.5,0.6,0.9,且三门课程考试是否及格相互之间没有影响.求:
(1)该应聘者用方案一通过考试的概率;
(2)该应聘者用方案二通过考试的概率.
7.(1)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学,,,,,3名女同学,,,现从这5名男同学和3名女同学中各随机选1人,求被选中且未被选中的概率.
8.甲、乙两人各射击一次,击中目标的概率分别是和.假设两人射击是否击中目标相互之间没有影响,每人每次射击是否击中目标相互之间也没有影响.
(1)求甲、乙各射击一次均击中目标的概率;
(2)求甲射击4次,恰有3次连续击中目标的概率;
(3)若乙在射击中出现连续2次未击中目标则会被终止射击,求乙恰好射击4次后被终止射击的概率.
10.2 事件的相互独立性 答案
一、知识梳理
1. .
2. 独立
二、重要题型
1.解:(1)有两个小孩的家庭,小孩为男孩、女孩的样本空间为Ω1={(男,男),(男,女),(女,男),(女,女)},共包含4个样本点,由等可能性知每个样本点发生的概率均为.
这时A={(男,女),(女,男)},B={(男,男),(男,女),(女,男)},
AB={(男,女),(女,男)},于是P(A)=,P(B)=,P(AB)=.
由此可知P(AB)≠P(A)P(B),所以事件A,B不相互独立.
(2)有三个小孩的家庭,小孩为男孩、女孩的样本空间为Ω2={(男,男,男),(男,男,女),(男,女,男),(女,男,男),(男,女,女),(女,男,女),(女,女,男),(女,女,女)},共包含8个样本点,由等可能性知每个样本点发生的概率均为.这时A包含6个样本点,B包含4个样本点,AB包含3个样本点.
于是P(A)==,P(B)==,P(AB)=,显然有P(AB)=P(A)P(B)成立.
从而事件A与B是相互独立的.
2.D. 由相互独立事件同时发生的概率可知,问题由乙答对的概率为P=0.6×0.5=0.3,故选D.
系统正常工作的情况分成两个步骤,A正常工作且B,C至少有一个正常工作的情况,A正常工作的概率为:0.7;B,C至少有一个正常工作的情况的概率为1减去B,C都不正常工作的情况的概率,即:B,C至少有一个正常工作的概率为:
1﹣(1﹣0.8)(1﹣0.9)=0.98,所以:这个系统正常工作的概率为:0.7×0.98=0.686;故答案为:0.686;
4.C. 一道数学难题,恰有一人解出,包括:
①A解出,B,C解不出,概率为××=;
②B解出,A,C解不出,概率为××=;
③C解出,A,B解不出,概率为××=.
所以恰有1人解出的概率为++=.
5.解:(1)由题意列出方程组,得:
,解得m=,n=.
(2)由题令该新同学在社团方面获得校本选修课学分的分数为Xi,
获得样本等候课学分分数不低于4分为事件A,
则P(X4)=,P(X5)==,P(X6)==,
P(A)=P(X4)+P(X5)+P(X6)==.
三、巩固练习
1.B 因为该试验的样本空间为Ω={1,2,3,4,5,6},A={2,4,6},B={3,6},AB={6},所以P(A)=,P(B)=,P(AB)==×=P(A)P(B),所以A与B是相互独立事件.
2. D 设甲独立破译密码的事件为A,乙独立破译密码的事件为B,则P(A)=,
P(B)=,所以P()=,P()=,所以甲、乙两人合作译出密码的概率为1-P()P()=1-×=.
3.D 由题意,P()·P()=,P()·P(B)=P(A)·P().
设P(A)=x,P(B)=y,则,即
∴x2-2x+1=,∴x-1=-,或x-1=(舍去),∴x=.
4.D 左上方2个箱子畅通的概率为,所以不畅通的概率为,
则左边3个箱子畅通的概率为.右边2个箱子畅通的概率为.
所以当开关合上时,电路畅通的概率是.
5. 设“国庆节放假,甲、乙、丙三人去北京旅游”分别为事件A、B、C,则A、B、C相互独立且P(A)=,P(B)=,P(C)=,∴至少有1人去北京旅游的概率为:
1-P( )=1-P()·P()·P()=1-××=1-=.
6.解:记该应聘者对三门指定课程考试及格的事件分别为A,B,C,则P(A)=0.5,P(B)=0.6,P(C)=0.9.
(1)应聘者用方案一通过考试的概率为P1=P(AB)+P(BC)+P(AC)+P(ABC)
=P(A)P(B)[1-P(C)]+[1-P(A)]P(B)P(C)+P(A)[1-P(B)]P(C)+P(A)P(B)P(C)
=0.5×0.6×0.1+0.5×0.6×0.9+0.5×0.4×0.9+0.5×0.6×0.9=0.75.
(2)从三门课程中随机选取两门的样本空间为Ω={AB,AC,BC},每个样本点发生的概率均为,因此,应聘者用方案二通过考试的概率为P2=P(AB)+P(BC)+P(AC)
=P(A)P(B)+P(B)P(C)+P(A)P(C)=×0.5×0.6+×0.6×0.9+×0.5×0.9
=0.43.
7.解:(1)由调查数据可知,既未参加书法社团又未参加演讲社团的有30人.
故至少参加上述一个社团的共有 (人),
所以从该班随机选1名同学,
该同学至少参加上述一个社团的概率为.
(2)从这5名男同学和3名女同学中各随机选1人,
其一切可能的结果组成的基本事件有: ,,
,,,,
,,,,,,
,共15个.根据题意,这些基本事件的出现是等可能的.
事件“被选中且未被选中”所包含的基本事件有:,,共2个.
因此被选中且未被选中的概率为.
8.解:(1)记事件A表示“甲击中目标”,事件B表示“乙击中目标”.
依题意知,事件A和事件B相互独立,因此甲、乙各射击一次均击中目标的概率为
P(AB)=P(A)P(B)=×=.
(2)记事件Ai表示“甲第i次射击击中目标”(其中i=1,2,3,4),并记“甲4次射击恰有3次连续击中目标”为事件C,则C=A1A2A34∪1A2A3A4,且A1A2A34与1A2A3A4是互斥事件.
由于A1,A2,A3,A4之间相互独立,所以Ai与j(i,j=1,2,3,4,且i≠j)之间也相互独立.
由于P(A1)=P(A2)=P(A3)=P(A4)=,P(1)=P(2)=P(3)=P(4)=,
故P(C)=P(A1A2A34∪1A2A3A4)=P(A1)P(A2)P(A3)P(4)+P(1)P(A2)P(A3)P(A4)
=3×+×3=.所以甲射击4次,恰有3次连续击中目标的概率为.
(3)记事件Bi表示“乙第i次射击击中目标”(其中i=1,2,3,4),并记事件D表示“乙在第4次射击后被终止射击”,则D=B1B234∪1B234,且B1B234与1B234是互斥事件.由于B1,B2,B3,B4之间相互独立,所以Bi与j(i,j=1,2,3,4,且i≠j)之间也相互独立.由于P(Bi)=(i=1,2,3,4),P(i)=(i=1,2,3,4),
故P(D)=P(B1B234∪1B234)=P(B1B234)+P(1B234)
=P(B1)P(B2)P(3)P(4)+P(1)P(B2)P(3)P(4)=2×2+×3=.
所以乙恰好射击4次后被终止射击的概率为.
一、知识梳理
1.相互独立事件:对于两个事件A与B,如果____________成立,则称事件A与事件B相互独立。
2. 相互独立事件的结论:如果事件A与事件B相互独立,那么A与,与B,与都_____。
二、重要题型
知识点一:事件独立性的判定
1.一个家庭中有若干个小孩,假定生男孩和生女孩是等可能的,令A={一个家庭中既有男孩又有女孩},B={一个家庭中最多有一个女孩}.对下述两种情形,讨论A与B的独立性:
(1)家庭中有两个小孩;
(2)家庭中有三个小孩.
知识点二:相互独立事件同时发生的概率
2.某人提出一个问题,甲先答,答对的概率为0.4,如果甲答错,由乙答,答对的概率为0.5,则问题由乙答对的概率为( )
A.0.2 B.0.8 C.0.4 D.0.3
3.若三个原件A,B,C按照如图的方式连接成一个系统,每个原件是否正常工作不受其他元件的影响,当原件A正常工作且B,C中至少有一个正常工作时,系统就正常工作,若原件A,B,C正常工作的概率依次为0.7,0.8,0.9,则这个系统正常工作的概率为
知识点三:相互独立事件的综合应用
4.有一道数学难题,学生A解出的概率为,学生B解出的概率为,学生C解出的概率为.若A,B,C三人独立去解答此题,则恰有一人解出的概率为( )
A.1 B. C. D.
5.某中学根据学生的兴趣爱好,分别创建了“书法”、“诗词”、“理学”三个社团,据资料统计新生通过考核选拔进入这三个社团成功与否相互独立.2015年某新生入学,假设他通过考核选拔进入该校的“书法”、“诗词”、“理学”三个社团的概率依次为m、、n,已知三个社团他都能进入的概率为,至少进入一个社团的概率为,且m>n.
(l)求m与n的值;
(2)该校根据三个社团活动安排情况,对进入“书法”社的同学增加校本选修学分1分,对进入“诗词”社的同学增加校本选修学分2分,对进入“理学”社的同学增加校本选修学分3分.求该新同学在社团方面获得校本选修课学分分数不低于4分的概率.
三、巩固练习
1.掷一枚骰子一次,记A表示事件“出现偶数点”,B表示事件“出现3点或6点”,则事件A与B的关系是( )
A.互斥事件 B.相互独立事件
C.既互斥又相互独立事件 D.既不互斥又不相互独立事件
2.甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为和,则两人合作译出密码的概率为( )
A. B. C. D.
3.设两个独立事件A和B都不发生的概率为,A发生B不发生的概率与B发生A不发生的概率相同,则事件A发生的概率P(A)是( )
A. B. C. D.
4.在如图所示的电路中,5只箱子表示保险匣,箱中所示数值表示通电时保险丝被熔断的概率,若各保险匣之间互不影响,则当开关合上时,电路畅通的概率是( )
A. B. C. D.
5.国庆节放假,甲、乙、丙三人去北京旅游的概率分别是,,.假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为________.
6.某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考三门课程,至少有两门及格为考试通过.
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别为0.5,0.6,0.9,且三门课程考试是否及格相互之间没有影响.求:
(1)该应聘者用方案一通过考试的概率;
(2)该应聘者用方案二通过考试的概率.
7.(1)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学,,,,,3名女同学,,,现从这5名男同学和3名女同学中各随机选1人,求被选中且未被选中的概率.
8.甲、乙两人各射击一次,击中目标的概率分别是和.假设两人射击是否击中目标相互之间没有影响,每人每次射击是否击中目标相互之间也没有影响.
(1)求甲、乙各射击一次均击中目标的概率;
(2)求甲射击4次,恰有3次连续击中目标的概率;
(3)若乙在射击中出现连续2次未击中目标则会被终止射击,求乙恰好射击4次后被终止射击的概率.
10.2 事件的相互独立性 答案
一、知识梳理
1. .
2. 独立
二、重要题型
1.解:(1)有两个小孩的家庭,小孩为男孩、女孩的样本空间为Ω1={(男,男),(男,女),(女,男),(女,女)},共包含4个样本点,由等可能性知每个样本点发生的概率均为.
这时A={(男,女),(女,男)},B={(男,男),(男,女),(女,男)},
AB={(男,女),(女,男)},于是P(A)=,P(B)=,P(AB)=.
由此可知P(AB)≠P(A)P(B),所以事件A,B不相互独立.
(2)有三个小孩的家庭,小孩为男孩、女孩的样本空间为Ω2={(男,男,男),(男,男,女),(男,女,男),(女,男,男),(男,女,女),(女,男,女),(女,女,男),(女,女,女)},共包含8个样本点,由等可能性知每个样本点发生的概率均为.这时A包含6个样本点,B包含4个样本点,AB包含3个样本点.
于是P(A)==,P(B)==,P(AB)=,显然有P(AB)=P(A)P(B)成立.
从而事件A与B是相互独立的.
2.D. 由相互独立事件同时发生的概率可知,问题由乙答对的概率为P=0.6×0.5=0.3,故选D.
系统正常工作的情况分成两个步骤,A正常工作且B,C至少有一个正常工作的情况,A正常工作的概率为:0.7;B,C至少有一个正常工作的情况的概率为1减去B,C都不正常工作的情况的概率,即:B,C至少有一个正常工作的概率为:
1﹣(1﹣0.8)(1﹣0.9)=0.98,所以:这个系统正常工作的概率为:0.7×0.98=0.686;故答案为:0.686;
4.C. 一道数学难题,恰有一人解出,包括:
①A解出,B,C解不出,概率为××=;
②B解出,A,C解不出,概率为××=;
③C解出,A,B解不出,概率为××=.
所以恰有1人解出的概率为++=.
5.解:(1)由题意列出方程组,得:
,解得m=,n=.
(2)由题令该新同学在社团方面获得校本选修课学分的分数为Xi,
获得样本等候课学分分数不低于4分为事件A,
则P(X4)=,P(X5)==,P(X6)==,
P(A)=P(X4)+P(X5)+P(X6)==.
三、巩固练习
1.B 因为该试验的样本空间为Ω={1,2,3,4,5,6},A={2,4,6},B={3,6},AB={6},所以P(A)=,P(B)=,P(AB)==×=P(A)P(B),所以A与B是相互独立事件.
2. D 设甲独立破译密码的事件为A,乙独立破译密码的事件为B,则P(A)=,
P(B)=,所以P()=,P()=,所以甲、乙两人合作译出密码的概率为1-P()P()=1-×=.
3.D 由题意,P()·P()=,P()·P(B)=P(A)·P().
设P(A)=x,P(B)=y,则,即
∴x2-2x+1=,∴x-1=-,或x-1=(舍去),∴x=.
4.D 左上方2个箱子畅通的概率为,所以不畅通的概率为,
则左边3个箱子畅通的概率为.右边2个箱子畅通的概率为.
所以当开关合上时,电路畅通的概率是.
5. 设“国庆节放假,甲、乙、丙三人去北京旅游”分别为事件A、B、C,则A、B、C相互独立且P(A)=,P(B)=,P(C)=,∴至少有1人去北京旅游的概率为:
1-P( )=1-P()·P()·P()=1-××=1-=.
6.解:记该应聘者对三门指定课程考试及格的事件分别为A,B,C,则P(A)=0.5,P(B)=0.6,P(C)=0.9.
(1)应聘者用方案一通过考试的概率为P1=P(AB)+P(BC)+P(AC)+P(ABC)
=P(A)P(B)[1-P(C)]+[1-P(A)]P(B)P(C)+P(A)[1-P(B)]P(C)+P(A)P(B)P(C)
=0.5×0.6×0.1+0.5×0.6×0.9+0.5×0.4×0.9+0.5×0.6×0.9=0.75.
(2)从三门课程中随机选取两门的样本空间为Ω={AB,AC,BC},每个样本点发生的概率均为,因此,应聘者用方案二通过考试的概率为P2=P(AB)+P(BC)+P(AC)
=P(A)P(B)+P(B)P(C)+P(A)P(C)=×0.5×0.6+×0.6×0.9+×0.5×0.9
=0.43.
7.解:(1)由调查数据可知,既未参加书法社团又未参加演讲社团的有30人.
故至少参加上述一个社团的共有 (人),
所以从该班随机选1名同学,
该同学至少参加上述一个社团的概率为.
(2)从这5名男同学和3名女同学中各随机选1人,
其一切可能的结果组成的基本事件有: ,,
,,,,
,,,,,,
,共15个.根据题意,这些基本事件的出现是等可能的.
事件“被选中且未被选中”所包含的基本事件有:,,共2个.
因此被选中且未被选中的概率为.
8.解:(1)记事件A表示“甲击中目标”,事件B表示“乙击中目标”.
依题意知,事件A和事件B相互独立,因此甲、乙各射击一次均击中目标的概率为
P(AB)=P(A)P(B)=×=.
(2)记事件Ai表示“甲第i次射击击中目标”(其中i=1,2,3,4),并记“甲4次射击恰有3次连续击中目标”为事件C,则C=A1A2A34∪1A2A3A4,且A1A2A34与1A2A3A4是互斥事件.
由于A1,A2,A3,A4之间相互独立,所以Ai与j(i,j=1,2,3,4,且i≠j)之间也相互独立.
由于P(A1)=P(A2)=P(A3)=P(A4)=,P(1)=P(2)=P(3)=P(4)=,
故P(C)=P(A1A2A34∪1A2A3A4)=P(A1)P(A2)P(A3)P(4)+P(1)P(A2)P(A3)P(A4)
=3×+×3=.所以甲射击4次,恰有3次连续击中目标的概率为.
(3)记事件Bi表示“乙第i次射击击中目标”(其中i=1,2,3,4),并记事件D表示“乙在第4次射击后被终止射击”,则D=B1B234∪1B234,且B1B234与1B234是互斥事件.由于B1,B2,B3,B4之间相互独立,所以Bi与j(i,j=1,2,3,4,且i≠j)之间也相互独立.由于P(Bi)=(i=1,2,3,4),P(i)=(i=1,2,3,4),
故P(D)=P(B1B234∪1B234)=P(B1B234)+P(1B234)
=P(B1)P(B2)P(3)P(4)+P(1)P(B2)P(3)P(4)=2×2+×3=.
所以乙恰好射击4次后被终止射击的概率为.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
