10.2 直方图 同步课时训练卷(解析版)
文档属性
| 名称 | 10.2 直方图 同步课时训练卷(解析版) |  | |
| 格式 | rar | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 09:52:43 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版七年级下册10.2《直方图》同步课时训练卷
班级__________姓名__________学号__________
一、选择题
1.某样本容量是60,分组后,第2组的频率是0.15,那么第2组的频数是( )
A.9 B.18 C.60 D.400
2.在一次调查中,出现种情况的频率为0.3,其余情况出现的频数之和为70,则这次调查的总数为( )
A.140 B.100 C.90 D.70
3.某班50名学生的身高被分为5组,第1至4组的频数分别为7、12、13、8,则第5组的频率是( )
A. B. C. D.
4.一组数据的最大值是44,最小值是9,制作频数分布表时取组距为5,为了使数据不落在边界上,应将这组数据分成( )
A.6组 B.7组 C.8组 D.9组
5.在某市2021年青少年航空航天模型锦标赛中,各年龄组的参赛人数情况如下表所示:
年龄组 13岁 14岁 15岁 16岁
参赛人数 5 19 12 14
若小明所在年龄组的参赛人数占全体参赛人数的38%,则小明所在的年龄组是( )
A.13岁 B.14岁 C.15岁 D.16岁
6.如图,这组数据的组数与组距分别为( )
A.5,9 B.6,9
C.5,10 D.6,10
7.某异地扶贫搬迁学生定点学校七年级共有1000人,为了了解这些学生的视力情况,从中抽查了20名学生的视力,对所得数据进行整理.若数据在4.8~5.1这一小组的频率为0.3,则可估计该校七年级学生视力在4.8~5.1范围内的人数有( )
A.600人 B.300人 C.150人 D.30人
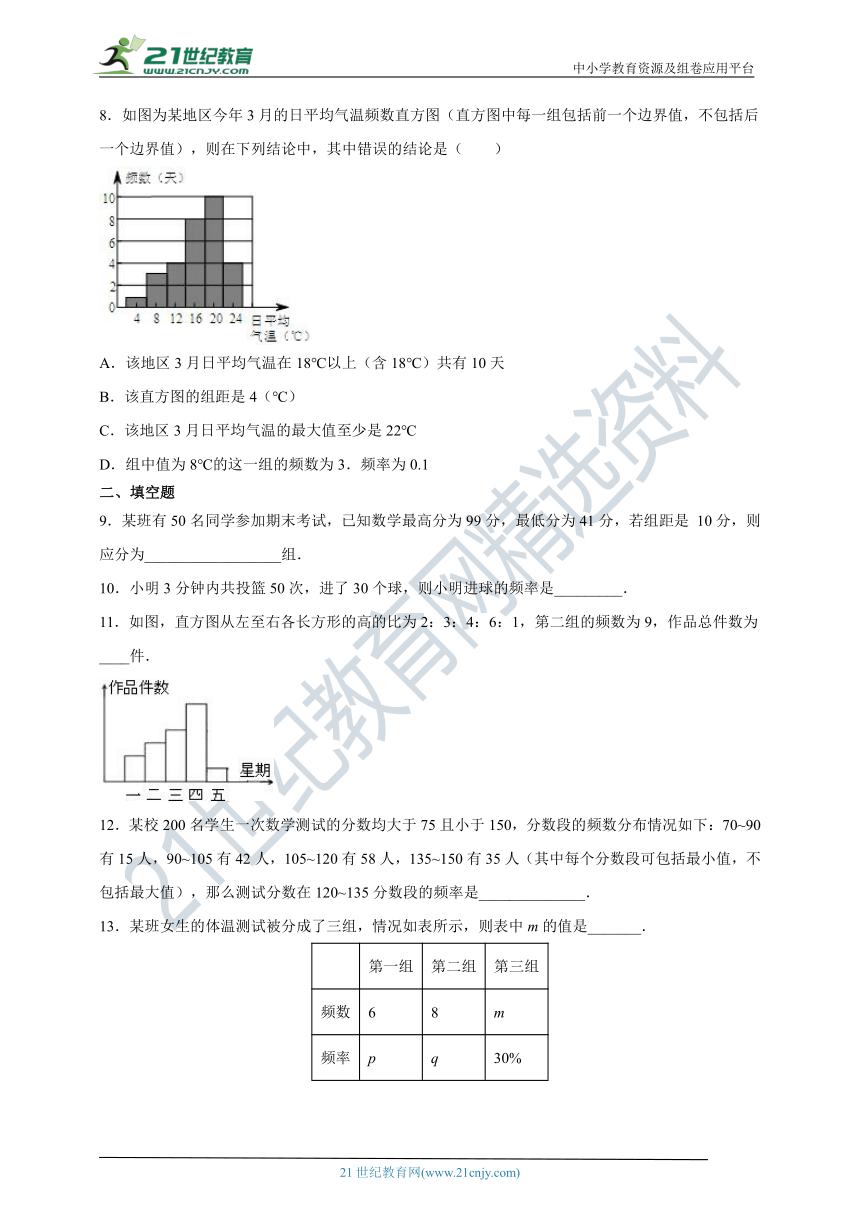
8.如图为某地区今年3月的日平均气温频数直方图(直方图中每一组包括前一个边界值,不包括后一个边界值),则在下列结论中,其中错误的结论是( )
A.该地区3月日平均气温在18℃以上(含18℃)共有10天
B.该直方图的组距是4(℃)
C.该地区3月日平均气温的最大值至少是22℃
D.组中值为8℃的这一组的频数为3.频率为0.1
二、填空题
9.某班有50名同学参加期末考试,已知数学最高分为99分,最低分为41分,若组距是 10分,则应分为__________________组.
10.小明3分钟内共投篮50次,进了30个球,则小明进球的频率是_________.
11.如图,直方图从左至右各长方形的高的比为2:3:4:6:1,第二组的频数为9,作品总件数为____件.
12.某校200名学生一次数学测试的分数均大于75且小于150,分数段的频数分布情况如下:70~90有15人,90~105有42人,105~120有58人,135~150有35人(其中每个分数段可包括最小值,不包括最大值),那么测试分数在120~135分数段的频率是______________.
13.某班女生的体温测试被分成了三组,情况如表所示,则表中m的值是_______.
第一组 第二组 第三组
频数 6 8 m
频率 p q 30%
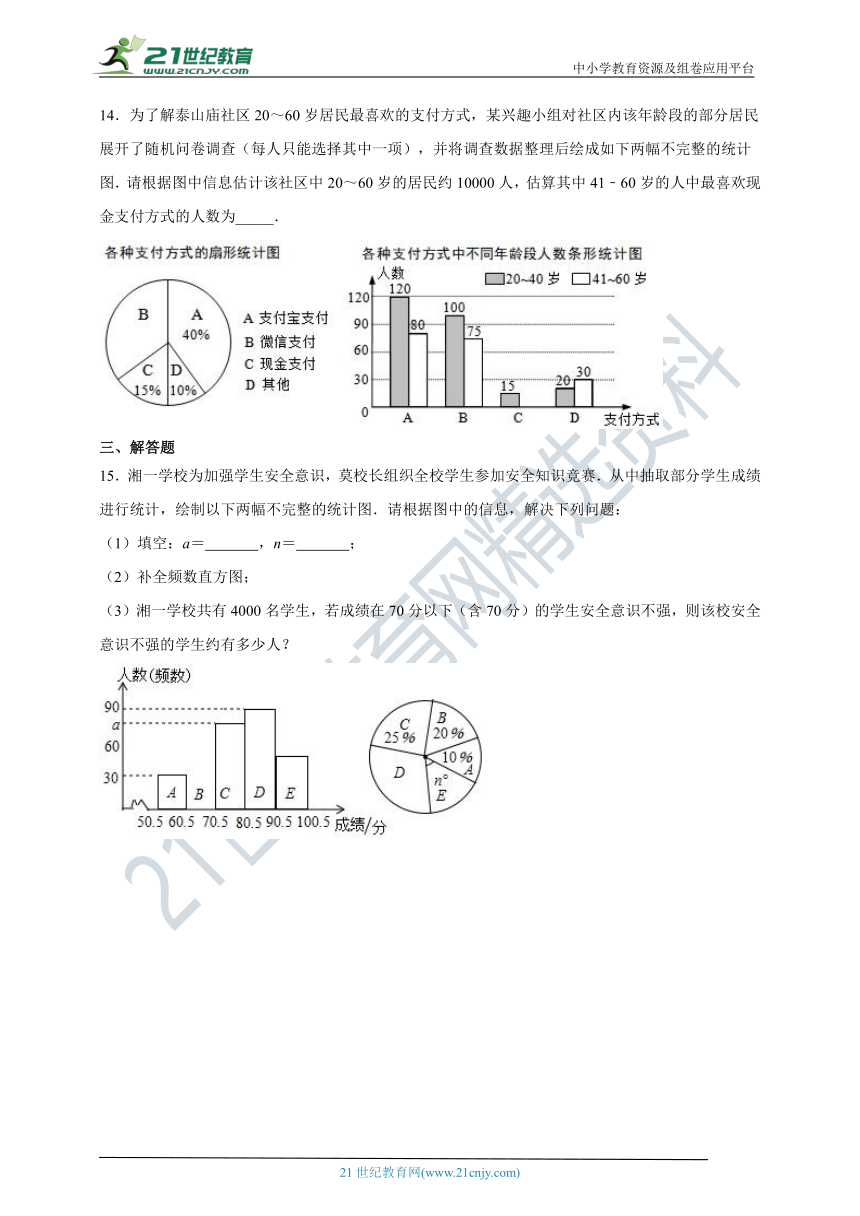
14.为了解泰山庙社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息估计该社区中20~60岁的居民约10000人,估算其中41﹣60岁的人中最喜欢现金支付方式的人数为_____.
三、解答题
15.湘一学校为加强学生安全意识,莫校长组织全校学生参加安全知识竞赛.从中抽取部分学生成绩进行统计,绘制以下两幅不完整的统计图.请根据图中的信息,解决下列问题:
(1)填空:a= ,n= ;
(2)补全频数直方图;
(3)湘一学校共有4000名学生,若成绩在70分以下(含70分)的学生安全意识不强,则该校安全意识不强的学生约有多少人?
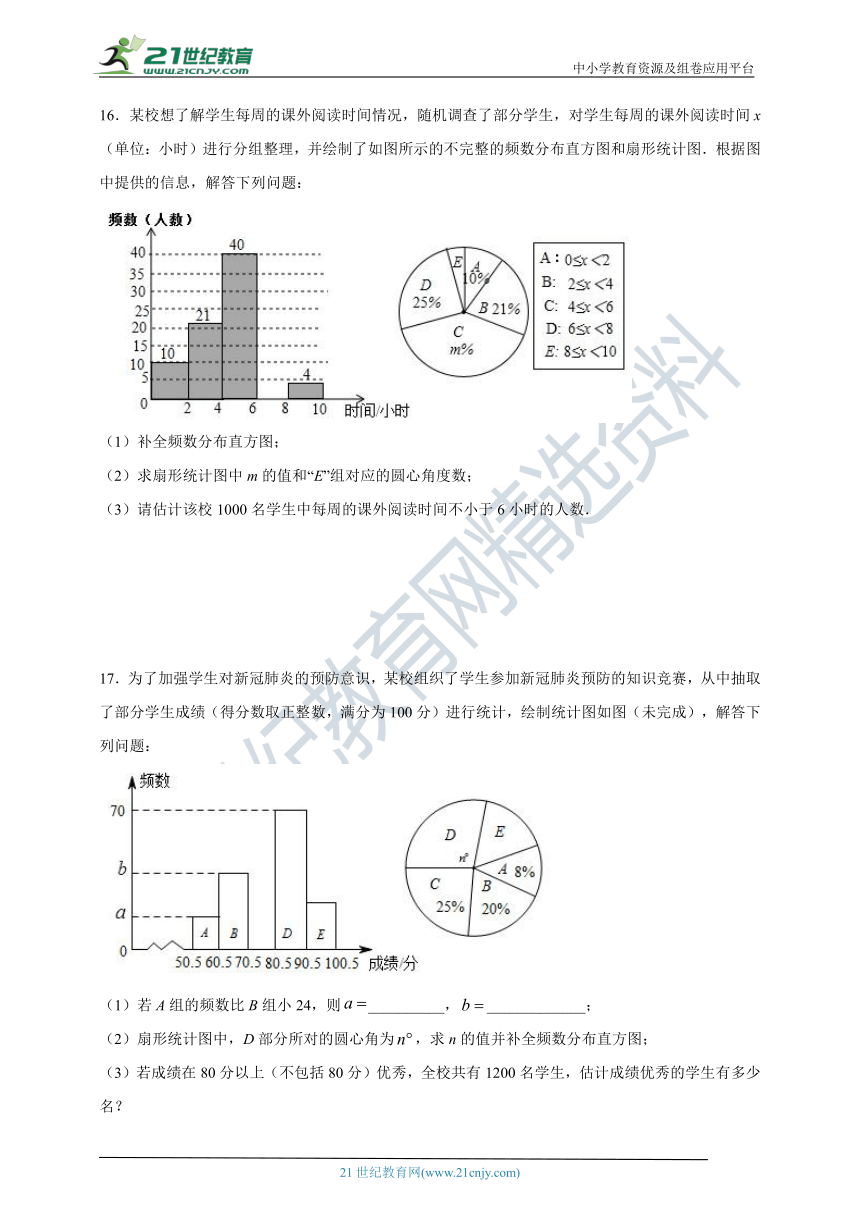
16.某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校1000名学生中每周的课外阅读时间不小于6小时的人数.
17.为了加强学生对新冠肺炎的预防意识,某校组织了学生参加新冠肺炎预防的知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如图(未完成),解答下列问题:
(1)若A组的频数比B组小24,则__________,_____________;
(2)扇形统计图中,D部分所对的圆心角为,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不包括80分)优秀,全校共有1200名学生,估计成绩优秀的学生有多少名?
18.某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分,请根据图表信息回答下列问题:
(1)本次调查的样本容量为 .
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
视力 频数(人) 频率
4.0≤x<4.3 20 0.1
4.3≤x<4.6 40 0.2
4.6≤x<4.9 70 0.35
4.9≤x<5.2 a 0.3
5.2≤x<5.5 10 b
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
19.在世界环境日(6月5日),学校组织了保护环境知识测试,现从中抽取部分学生的成绩作为样本,按“优秀”“良好”“合格”“不合格”等四个等级进行统计,绘制了如下尚不完整的统计图表:
测试成绩统计表
等级 频数 频率
优秀 30 a
良好 b 0.45
合格 24 0.20
不合格 12 0.10
合计 c 1
根据统计图表提供的信息,解答下列问题:
(1)表中a= ,b= ,c= .
(2)补全条形统计图.
(3)若该校有800名学生参加了本次测试,估计成绩等级在良好以上(包括良好)的学生约有多少人?
20.某学校开展了主题为“我帮父母做家务”的实践活动,倡导学生心怀感恩、孝敬父母,在家多帮父母做家务.校学生会在七、八、九三个年级随机抽取了部分学生,就“平均每天帮父母做家务所用时长”进行了调查,过程如下:
(收集数据)
做家务所用时长t(分钟)级别:
A:;B:;C:;D:;E:;
通过调查得到的一组数据:
(整理数据)
抽样调查50名学生帮父母做家务所用时长人数统计表
做家务所用时长级别 频数
A: 4
B: 8
C: 10
D: 18
E: 10
(描述数据)
(1)补全条形统计图;
(2)图2是根据该校初中各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,若该校七年级共有400名学生,请你估计全校学生中帮父母做家务所用时长不低于半小时(包含半小时)人数约为多少?
(3)根据本次实践活动主题,假如你是学生会中的一员,请你给全校同学发出一条倡议.
参考答案
1.A
【分析】
利用频数=频率×样本容量直接计算即可.
【详解】
解: 样本容量是60,分组后,第2组的频率是0.15,
第2组的频数是,
故答案为:A.
【点睛】
本题考查了频数与频率的知识,解题的关键是能够了解它们之间的关系,难度不大.
2.B
【分析】
先求出其余情况出现的频率,然后根据求解.
【详解】
解:其余情况出现的频率=1?0.3=0.7,
则这次调查的总数为:70÷0.7=100.
故选:B.
【点睛】
本题考查了频数和频率,掌握频率的计算公式是解答本题的关键.
3.C
【分析】
先求得第5组的频数,再除以总学生数即可.
【详解】
由第5组频数为:,得第五组的频率为.
故选:C.
【点睛】
此题考查频数与频率的关系,知道所有频数之和为样本容量及每组频率等于其频数与样本容量的商是关键.
4.C
【分析】
根据极差与组距的关系可知这组数据的组数.
【详解】
解:∵极差为44-9=35,组距为5,
∴35÷5=7,7+1=8,
则为了使数据不落在边界上,应将这组数据分成8组,
故选:C.
【点睛】
本题考查了样本数据中极差、组距和组数的关系,是基础题型.注意数据不落在边界上,商是整数时组数应该加上1.
5.B
【分析】
根据各年龄组的参赛人数情况表,算出总人数,再算出14岁年龄组人数所占的百分比,即可得到答案.
【详解】
解:根据各年龄组的参赛人数情况表可知:
总参赛人数为:5+19+12+14=50,
19÷50=38%,
则小明所在的年龄组是14岁.
故选:B.
【点睛】
本题考查了频数与频率,解决本题的关键是掌握频数与频率的关系,理清频数分布表的数据.
6.D
【分析】
通过观察频率分布直方图,发现一共分为6组,每一组的最大值和最小值的差都是10,做出判断.
【详解】
解:频率分布直方图中共有6个直条,故组数是6,每组的最大值和最小值的差都是10,因此组距是10,
故选:D.
【点睛】
考查频率分布直方图的制作方法,明确组距、组数的意义是绘制频率分布直方图的两个基本的步骤.
7.B
【分析】
由数据在4.8~5.1这一小组的频率为0.3,则利用总体的总量乘以这个频率即可得到答案.
【详解】
解: 数据在4.8~5.1这一小组的频率为0.3,
可估计该校七年级学生视力在4.8~5.1范围内的人数有:(人),
故选:
【点睛】
本题考查的是利用样本估计总体,频率的含义,利用样本的某种占比估计总体相应小组的总量是解题的关键.
8.A
【分析】
根据频数分布直方图的中各组的频数分布逐一分析判断可得.
【详解】
解:A、该地区3月日平均气温在18℃以上(含18℃)共有10+4=14天,故此结论错误;
B、该直方图的组距是8-4=4(℃),故此结论正确;
C、该地区4月日平均气温的最大值至少是22℃,此结论正确;
D、组中值为8℃的这一组的频数为3.频数为=0.1,此结论正确;
故选:A.
【点睛】
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
9.6
【分析】
首先计算出最大值与最小值的差,再利用极差除以组距即可.
【详解】
解:99-41=58,
58÷10≈6,
故答案为6.
【点睛】
本题考查了频数分布表.首先计算极差,即计算最大值与最小值的差,再决定组距与组数.
10.0.6
【分析】
根据频率、频数的关系:频率=频数÷数据总和,可知小明进球的频率.
【详解】
解:∵小明共投篮50次,进了30个球,
∴小明进球的频率=30÷50=0.6.
故答案为:0.6.
【点睛】
本题考查频率、频数、总数的关系:频率=频数÷数据总和.
11.48
【分析】
由各长方形的高的比得到各段的频率之比,即可得到第二组的频率,再由数据总和=某段的频数÷该段的频率,即可计算作品总数.
【详解】
∵从左至右各长方形的高的比为2:3:4:6:1,
∴频率之比为2:3:4:6:1;
∴第二组的频率,
∵第二组的频数为9,
∴作品有948(件).
故答案为:48.
【点睛】
本题考查了频数分布直方图,熟练掌握频数分布直方图的意义是解题的关键.
12.0.25
【分析】
根据已知75~90、90~105、105~120、135~150的频数,求出120~135分数段的频数,然后根据频率=即可求出测试分数在120~135分数段的频率.
【详解】
解:120~135分数段的频数=200-15-42-58-35=50人,
则测试分数在120~135分数段的频率==0.25.
故答案为:0.25.
【点睛】
本题考查了频数和频率的知识,解题的关键是求出相应分数段的频数.
13.6
【分析】
根据各小组的频率之和等于1,即可得出第一组与第二组的频率和,然后求出数据总数,从而求出m的值.
【详解】
解:∵第一组与第二组的频率之和为1-30%=70%,
∴该班男生的总人数为(6+8)÷70%=20,
∴m= 20×30%=6.
故答案为:6.
【点睛】
本题主要考查了频数与频率,频率是指每个对象出现的次数与总次数的比值(或者百分比),即频率=频数÷总数.
14.1200人.
【分析】
根据喜欢支付宝支付的人数÷其所占各种支付方式的比例=参与问卷调查的总人数,由喜欢现金支付的人数(41~60岁)=参与问卷调查的总人数×现金支付所占各种支付方式的比例﹣15,即可求出喜欢现金支付的人数(41~60岁),再用社区总人数乘以样本中41﹣60岁的人中最喜欢现金支付方式的人数所占比例即可.
【详解】
解:∵参与问卷调查的总人数为(120+80)÷40%=500(人),
∴41﹣60岁的人中最喜欢现金支付方式的人数500×15%﹣15=60(人).
则该社区41﹣60岁的人中最喜欢现金支付方式的人数为10000×=1200(人),
故答案为:1200人.
【点睛】
本题考查条形统计图,扇形统计图,样本估计总体等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
15.(1)75,54;(2)60,补图见解答;(3)1200人.
【分析】
(1)先由A组人数及其所占百分比求出总人数,再用360°乘以E组人数所占比例即可得;
(2)用总人数乘以B组所占的百分比求出B组的人数,再补全统计图即可;
(3)利用样本估计总体思想求解可得.
【详解】
解:(1)∵被调查的总人数为30÷10%=300(人),
∴a=300×25%=75,
则E组人数为300﹣(30+60+75+90)=45,
∴n=360×=54,
故答案为:75、54;
(2)B组人数为:300×20%=60(人),
补全直方图如下:
(3)该校安全意识不强的学生约有4000×(10%+20%)=1200(人).
【点睛】
本题考查了频数(率)分布直方图,用样本估计总体,读懂题意,熟悉相关性质是解题的关键.
16.(1)图见详解;(2)m=40,“E”组对应的圆心角的度数为14.4°;(3)该校1000名学生中每周的课外阅读时间不小于6小时的人数为290名.
【分析】
(1)根据统计图可得随机抽查的学生总人数为21÷21%=100名,进而可得“D”组人数为100×25%=25名,然后可得频数分布直方图;
(2)由(1)及统计图可直接进行求解;
(3)由统计图可直接进行求解.
【详解】
解:(1)由统计图可得:随机抽查的学生总人数为21÷21%=100名,
∴“D”组人数为100×25%=25名,
补全频数分布直方图如图所示:
(2)由(1)及统计图可得:
,
“E”组对应的圆心角的度数为;
(3)由题意得:
(名);
答:该校1000名学生中每周的课外阅读时间不小于6小时的人数为290名.
【点睛】
本题主要考查频数分布直方图及扇形统计图,熟练掌握频数分布直方图及扇形统计图是解题的关键.
17.(1)16,40;(2)n=126,图见详解;(3)成绩优秀的学生有564名.
【分析】
(1)从统计图中可知A组比B组少12%,然后可根据题意进行求解;
(2)由题意可先求出D部分所占百分比,然后再求出圆心角的度数即可,最后根据题意补全频数分布直方图;
(3)利用样本估计总体结合题意可直接进行求解.
【详解】
解:(1)由统计图及题意可得:抽取的总人数=24÷(20%-8%)=200(名),
∴(名),(名),
故答案为16,40;
(2)由图及(1)可得:
,
C组人数为:(人),
∴E组人数为:200-16-40-50-70=24(人),补全频数分布直方图如图所示:
(3)由(2)及题意可得:
(名);
答:成绩优秀的学生有564名.
【点睛】
本题主要考查频数分布直方图及扇形统计图,熟练掌握频数分布直方图及扇形统计图是解题的关键.
18.(1)200;(2)60;0.05;见解析;(3)3500人.
【分析】
(1)用第1组的频数除以它所占的百分比即可得到样本容量;
(2)用样本容量乘以0.3得到a的值,用10除以10得到b的值;
(3)用样本值后面三组的频率和乘以5000可估计全区初中毕业生中视力正常的学生数.
【详解】
解:(1)20÷0.1=200(人),
所以本次调查的样本为200名初中毕业生的视力情况,样本容量为200,
故答案为:200;
(2)a=200×0.3=60,b=10÷200=0.05,
补全图形如下:
故答案为:60,0.05;
(3)5000×(0.35+0.3+0.05)=3500(人),
答:估计全区初中毕业生中视力正常的学生有3500人.
【点睛】
本题考查频数分布图、条形统计图、用样本估计整体等知识,是重要考点,难度较易,掌握相关知识是解题关键.
19.(1)0.25,54,120;(2)见解析;(3)560人
【分析】
(1)根据合格的频数和频率可以求得本次调查的人数,然后即可得到a、b、c的值;
(2)根据(1)中b的值,可以将条形统计图补充完整;
(3)根据频数分布表中的数据,计算成绩在良好以上的频率,利用样本估计总体,可以计算出测试成绩等级在良好以上(包括良好)的学生约有多少人.
【详解】
解:(1)本次抽取的学生有:c=24÷0.20=120(人),
a=30÷120=0.25,b=120×0.45=54,c=120,
故答案为:0.25,54,120;
(2)由(1)知,b=54,
补全的条形统计图如右图所示;
(3)(人).
答:测试成绩等级在良好以上(包括良好)的学生约有560人.
【点睛】
本题考查条形统计图、频数分布表、用样本估计总体,明确题意,理解频数,频率与总体的关系是解题关键.
20.(1)见解析;(2)560人;(3)感恩父母,从我做起,从身边小事做起(合理即可)
【分析】
(1)根据统计表补全统计图即可;
(2)求出样本中帮父母做家务所用时长不低于半小时的百分比,再求出全校学生数,乘以百分比即可;
(3)倡议合理即可.
【详解】
解:(1)补全条形统计图如图所示:
(2)由题可知:帮父母做家务所用时长在半小时以上(包含半小时)的人数为28人,
所以.
因为七年级总人数占全校总人数的40%,而七年级学生人数为400人,所以全校共有人,由样本中得到:帮父母做家务所用时长在半小时以上(包含半小时)的人数所占的百分比为56%,所以全校学生中帮父母做家务所用时长在半小时以上(包含半小时)人数约人.
答:全校学生中帮父母做家务所用时长在半小时以上(包含半小时)人数约560人.
(3)感恩父母,从我做起,从身边小事做起(合理即可).
【点睛】
本题考查了数据的收集、整理与描述,用样本估计总体,解题关键是熟练运用统计知识进行整理与描述,通过样本数据准确估计总体数据
_21?????????è?????(www.21cnjy.com)_
人教版七年级下册10.2《直方图》同步课时训练卷
班级__________姓名__________学号__________
一、选择题
1.某样本容量是60,分组后,第2组的频率是0.15,那么第2组的频数是( )
A.9 B.18 C.60 D.400
2.在一次调查中,出现种情况的频率为0.3,其余情况出现的频数之和为70,则这次调查的总数为( )
A.140 B.100 C.90 D.70
3.某班50名学生的身高被分为5组,第1至4组的频数分别为7、12、13、8,则第5组的频率是( )
A. B. C. D.
4.一组数据的最大值是44,最小值是9,制作频数分布表时取组距为5,为了使数据不落在边界上,应将这组数据分成( )
A.6组 B.7组 C.8组 D.9组
5.在某市2021年青少年航空航天模型锦标赛中,各年龄组的参赛人数情况如下表所示:
年龄组 13岁 14岁 15岁 16岁
参赛人数 5 19 12 14
若小明所在年龄组的参赛人数占全体参赛人数的38%,则小明所在的年龄组是( )
A.13岁 B.14岁 C.15岁 D.16岁
6.如图,这组数据的组数与组距分别为( )
A.5,9 B.6,9
C.5,10 D.6,10
7.某异地扶贫搬迁学生定点学校七年级共有1000人,为了了解这些学生的视力情况,从中抽查了20名学生的视力,对所得数据进行整理.若数据在4.8~5.1这一小组的频率为0.3,则可估计该校七年级学生视力在4.8~5.1范围内的人数有( )
A.600人 B.300人 C.150人 D.30人
8.如图为某地区今年3月的日平均气温频数直方图(直方图中每一组包括前一个边界值,不包括后一个边界值),则在下列结论中,其中错误的结论是( )
A.该地区3月日平均气温在18℃以上(含18℃)共有10天
B.该直方图的组距是4(℃)
C.该地区3月日平均气温的最大值至少是22℃
D.组中值为8℃的这一组的频数为3.频率为0.1
二、填空题
9.某班有50名同学参加期末考试,已知数学最高分为99分,最低分为41分,若组距是 10分,则应分为__________________组.
10.小明3分钟内共投篮50次,进了30个球,则小明进球的频率是_________.
11.如图,直方图从左至右各长方形的高的比为2:3:4:6:1,第二组的频数为9,作品总件数为____件.
12.某校200名学生一次数学测试的分数均大于75且小于150,分数段的频数分布情况如下:70~90有15人,90~105有42人,105~120有58人,135~150有35人(其中每个分数段可包括最小值,不包括最大值),那么测试分数在120~135分数段的频率是______________.
13.某班女生的体温测试被分成了三组,情况如表所示,则表中m的值是_______.
第一组 第二组 第三组
频数 6 8 m
频率 p q 30%
14.为了解泰山庙社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息估计该社区中20~60岁的居民约10000人,估算其中41﹣60岁的人中最喜欢现金支付方式的人数为_____.
三、解答题
15.湘一学校为加强学生安全意识,莫校长组织全校学生参加安全知识竞赛.从中抽取部分学生成绩进行统计,绘制以下两幅不完整的统计图.请根据图中的信息,解决下列问题:
(1)填空:a= ,n= ;
(2)补全频数直方图;
(3)湘一学校共有4000名学生,若成绩在70分以下(含70分)的学生安全意识不强,则该校安全意识不强的学生约有多少人?
16.某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校1000名学生中每周的课外阅读时间不小于6小时的人数.
17.为了加强学生对新冠肺炎的预防意识,某校组织了学生参加新冠肺炎预防的知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如图(未完成),解答下列问题:
(1)若A组的频数比B组小24,则__________,_____________;
(2)扇形统计图中,D部分所对的圆心角为,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不包括80分)优秀,全校共有1200名学生,估计成绩优秀的学生有多少名?
18.某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分,请根据图表信息回答下列问题:
(1)本次调查的样本容量为 .
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
视力 频数(人) 频率
4.0≤x<4.3 20 0.1
4.3≤x<4.6 40 0.2
4.6≤x<4.9 70 0.35
4.9≤x<5.2 a 0.3
5.2≤x<5.5 10 b
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
19.在世界环境日(6月5日),学校组织了保护环境知识测试,现从中抽取部分学生的成绩作为样本,按“优秀”“良好”“合格”“不合格”等四个等级进行统计,绘制了如下尚不完整的统计图表:
测试成绩统计表
等级 频数 频率
优秀 30 a
良好 b 0.45
合格 24 0.20
不合格 12 0.10
合计 c 1
根据统计图表提供的信息,解答下列问题:
(1)表中a= ,b= ,c= .
(2)补全条形统计图.
(3)若该校有800名学生参加了本次测试,估计成绩等级在良好以上(包括良好)的学生约有多少人?
20.某学校开展了主题为“我帮父母做家务”的实践活动,倡导学生心怀感恩、孝敬父母,在家多帮父母做家务.校学生会在七、八、九三个年级随机抽取了部分学生,就“平均每天帮父母做家务所用时长”进行了调查,过程如下:
(收集数据)
做家务所用时长t(分钟)级别:
A:;B:;C:;D:;E:;
通过调查得到的一组数据:
(整理数据)
抽样调查50名学生帮父母做家务所用时长人数统计表
做家务所用时长级别 频数
A: 4
B: 8
C: 10
D: 18
E: 10
(描述数据)
(1)补全条形统计图;
(2)图2是根据该校初中各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,若该校七年级共有400名学生,请你估计全校学生中帮父母做家务所用时长不低于半小时(包含半小时)人数约为多少?
(3)根据本次实践活动主题,假如你是学生会中的一员,请你给全校同学发出一条倡议.
参考答案
1.A
【分析】
利用频数=频率×样本容量直接计算即可.
【详解】
解: 样本容量是60,分组后,第2组的频率是0.15,
第2组的频数是,
故答案为:A.
【点睛】
本题考查了频数与频率的知识,解题的关键是能够了解它们之间的关系,难度不大.
2.B
【分析】
先求出其余情况出现的频率,然后根据求解.
【详解】
解:其余情况出现的频率=1?0.3=0.7,
则这次调查的总数为:70÷0.7=100.
故选:B.
【点睛】
本题考查了频数和频率,掌握频率的计算公式是解答本题的关键.
3.C
【分析】
先求得第5组的频数,再除以总学生数即可.
【详解】
由第5组频数为:,得第五组的频率为.
故选:C.
【点睛】
此题考查频数与频率的关系,知道所有频数之和为样本容量及每组频率等于其频数与样本容量的商是关键.
4.C
【分析】
根据极差与组距的关系可知这组数据的组数.
【详解】
解:∵极差为44-9=35,组距为5,
∴35÷5=7,7+1=8,
则为了使数据不落在边界上,应将这组数据分成8组,
故选:C.
【点睛】
本题考查了样本数据中极差、组距和组数的关系,是基础题型.注意数据不落在边界上,商是整数时组数应该加上1.
5.B
【分析】
根据各年龄组的参赛人数情况表,算出总人数,再算出14岁年龄组人数所占的百分比,即可得到答案.
【详解】
解:根据各年龄组的参赛人数情况表可知:
总参赛人数为:5+19+12+14=50,
19÷50=38%,
则小明所在的年龄组是14岁.
故选:B.
【点睛】
本题考查了频数与频率,解决本题的关键是掌握频数与频率的关系,理清频数分布表的数据.
6.D
【分析】
通过观察频率分布直方图,发现一共分为6组,每一组的最大值和最小值的差都是10,做出判断.
【详解】
解:频率分布直方图中共有6个直条,故组数是6,每组的最大值和最小值的差都是10,因此组距是10,
故选:D.
【点睛】
考查频率分布直方图的制作方法,明确组距、组数的意义是绘制频率分布直方图的两个基本的步骤.
7.B
【分析】
由数据在4.8~5.1这一小组的频率为0.3,则利用总体的总量乘以这个频率即可得到答案.
【详解】
解: 数据在4.8~5.1这一小组的频率为0.3,
可估计该校七年级学生视力在4.8~5.1范围内的人数有:(人),
故选:
【点睛】
本题考查的是利用样本估计总体,频率的含义,利用样本的某种占比估计总体相应小组的总量是解题的关键.
8.A
【分析】
根据频数分布直方图的中各组的频数分布逐一分析判断可得.
【详解】
解:A、该地区3月日平均气温在18℃以上(含18℃)共有10+4=14天,故此结论错误;
B、该直方图的组距是8-4=4(℃),故此结论正确;
C、该地区4月日平均气温的最大值至少是22℃,此结论正确;
D、组中值为8℃的这一组的频数为3.频数为=0.1,此结论正确;
故选:A.
【点睛】
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
9.6
【分析】
首先计算出最大值与最小值的差,再利用极差除以组距即可.
【详解】
解:99-41=58,
58÷10≈6,
故答案为6.
【点睛】
本题考查了频数分布表.首先计算极差,即计算最大值与最小值的差,再决定组距与组数.
10.0.6
【分析】
根据频率、频数的关系:频率=频数÷数据总和,可知小明进球的频率.
【详解】
解:∵小明共投篮50次,进了30个球,
∴小明进球的频率=30÷50=0.6.
故答案为:0.6.
【点睛】
本题考查频率、频数、总数的关系:频率=频数÷数据总和.
11.48
【分析】
由各长方形的高的比得到各段的频率之比,即可得到第二组的频率,再由数据总和=某段的频数÷该段的频率,即可计算作品总数.
【详解】
∵从左至右各长方形的高的比为2:3:4:6:1,
∴频率之比为2:3:4:6:1;
∴第二组的频率,
∵第二组的频数为9,
∴作品有948(件).
故答案为:48.
【点睛】
本题考查了频数分布直方图,熟练掌握频数分布直方图的意义是解题的关键.
12.0.25
【分析】
根据已知75~90、90~105、105~120、135~150的频数,求出120~135分数段的频数,然后根据频率=即可求出测试分数在120~135分数段的频率.
【详解】
解:120~135分数段的频数=200-15-42-58-35=50人,
则测试分数在120~135分数段的频率==0.25.
故答案为:0.25.
【点睛】
本题考查了频数和频率的知识,解题的关键是求出相应分数段的频数.
13.6
【分析】
根据各小组的频率之和等于1,即可得出第一组与第二组的频率和,然后求出数据总数,从而求出m的值.
【详解】
解:∵第一组与第二组的频率之和为1-30%=70%,
∴该班男生的总人数为(6+8)÷70%=20,
∴m= 20×30%=6.
故答案为:6.
【点睛】
本题主要考查了频数与频率,频率是指每个对象出现的次数与总次数的比值(或者百分比),即频率=频数÷总数.
14.1200人.
【分析】
根据喜欢支付宝支付的人数÷其所占各种支付方式的比例=参与问卷调查的总人数,由喜欢现金支付的人数(41~60岁)=参与问卷调查的总人数×现金支付所占各种支付方式的比例﹣15,即可求出喜欢现金支付的人数(41~60岁),再用社区总人数乘以样本中41﹣60岁的人中最喜欢现金支付方式的人数所占比例即可.
【详解】
解:∵参与问卷调查的总人数为(120+80)÷40%=500(人),
∴41﹣60岁的人中最喜欢现金支付方式的人数500×15%﹣15=60(人).
则该社区41﹣60岁的人中最喜欢现金支付方式的人数为10000×=1200(人),
故答案为:1200人.
【点睛】
本题考查条形统计图,扇形统计图,样本估计总体等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
15.(1)75,54;(2)60,补图见解答;(3)1200人.
【分析】
(1)先由A组人数及其所占百分比求出总人数,再用360°乘以E组人数所占比例即可得;
(2)用总人数乘以B组所占的百分比求出B组的人数,再补全统计图即可;
(3)利用样本估计总体思想求解可得.
【详解】
解:(1)∵被调查的总人数为30÷10%=300(人),
∴a=300×25%=75,
则E组人数为300﹣(30+60+75+90)=45,
∴n=360×=54,
故答案为:75、54;
(2)B组人数为:300×20%=60(人),
补全直方图如下:
(3)该校安全意识不强的学生约有4000×(10%+20%)=1200(人).
【点睛】
本题考查了频数(率)分布直方图,用样本估计总体,读懂题意,熟悉相关性质是解题的关键.
16.(1)图见详解;(2)m=40,“E”组对应的圆心角的度数为14.4°;(3)该校1000名学生中每周的课外阅读时间不小于6小时的人数为290名.
【分析】
(1)根据统计图可得随机抽查的学生总人数为21÷21%=100名,进而可得“D”组人数为100×25%=25名,然后可得频数分布直方图;
(2)由(1)及统计图可直接进行求解;
(3)由统计图可直接进行求解.
【详解】
解:(1)由统计图可得:随机抽查的学生总人数为21÷21%=100名,
∴“D”组人数为100×25%=25名,
补全频数分布直方图如图所示:
(2)由(1)及统计图可得:
,
“E”组对应的圆心角的度数为;
(3)由题意得:
(名);
答:该校1000名学生中每周的课外阅读时间不小于6小时的人数为290名.
【点睛】
本题主要考查频数分布直方图及扇形统计图,熟练掌握频数分布直方图及扇形统计图是解题的关键.
17.(1)16,40;(2)n=126,图见详解;(3)成绩优秀的学生有564名.
【分析】
(1)从统计图中可知A组比B组少12%,然后可根据题意进行求解;
(2)由题意可先求出D部分所占百分比,然后再求出圆心角的度数即可,最后根据题意补全频数分布直方图;
(3)利用样本估计总体结合题意可直接进行求解.
【详解】
解:(1)由统计图及题意可得:抽取的总人数=24÷(20%-8%)=200(名),
∴(名),(名),
故答案为16,40;
(2)由图及(1)可得:
,
C组人数为:(人),
∴E组人数为:200-16-40-50-70=24(人),补全频数分布直方图如图所示:
(3)由(2)及题意可得:
(名);
答:成绩优秀的学生有564名.
【点睛】
本题主要考查频数分布直方图及扇形统计图,熟练掌握频数分布直方图及扇形统计图是解题的关键.
18.(1)200;(2)60;0.05;见解析;(3)3500人.
【分析】
(1)用第1组的频数除以它所占的百分比即可得到样本容量;
(2)用样本容量乘以0.3得到a的值,用10除以10得到b的值;
(3)用样本值后面三组的频率和乘以5000可估计全区初中毕业生中视力正常的学生数.
【详解】
解:(1)20÷0.1=200(人),
所以本次调查的样本为200名初中毕业生的视力情况,样本容量为200,
故答案为:200;
(2)a=200×0.3=60,b=10÷200=0.05,
补全图形如下:
故答案为:60,0.05;
(3)5000×(0.35+0.3+0.05)=3500(人),
答:估计全区初中毕业生中视力正常的学生有3500人.
【点睛】
本题考查频数分布图、条形统计图、用样本估计整体等知识,是重要考点,难度较易,掌握相关知识是解题关键.
19.(1)0.25,54,120;(2)见解析;(3)560人
【分析】
(1)根据合格的频数和频率可以求得本次调查的人数,然后即可得到a、b、c的值;
(2)根据(1)中b的值,可以将条形统计图补充完整;
(3)根据频数分布表中的数据,计算成绩在良好以上的频率,利用样本估计总体,可以计算出测试成绩等级在良好以上(包括良好)的学生约有多少人.
【详解】
解:(1)本次抽取的学生有:c=24÷0.20=120(人),
a=30÷120=0.25,b=120×0.45=54,c=120,
故答案为:0.25,54,120;
(2)由(1)知,b=54,
补全的条形统计图如右图所示;
(3)(人).
答:测试成绩等级在良好以上(包括良好)的学生约有560人.
【点睛】
本题考查条形统计图、频数分布表、用样本估计总体,明确题意,理解频数,频率与总体的关系是解题关键.
20.(1)见解析;(2)560人;(3)感恩父母,从我做起,从身边小事做起(合理即可)
【分析】
(1)根据统计表补全统计图即可;
(2)求出样本中帮父母做家务所用时长不低于半小时的百分比,再求出全校学生数,乘以百分比即可;
(3)倡议合理即可.
【详解】
解:(1)补全条形统计图如图所示:
(2)由题可知:帮父母做家务所用时长在半小时以上(包含半小时)的人数为28人,
所以.
因为七年级总人数占全校总人数的40%,而七年级学生人数为400人,所以全校共有人,由样本中得到:帮父母做家务所用时长在半小时以上(包含半小时)的人数所占的百分比为56%,所以全校学生中帮父母做家务所用时长在半小时以上(包含半小时)人数约人.
答:全校学生中帮父母做家务所用时长在半小时以上(包含半小时)人数约560人.
(3)感恩父母,从我做起,从身边小事做起(合理即可).
【点睛】
本题考查了数据的收集、整理与描述,用样本估计总体,解题关键是熟练运用统计知识进行整理与描述,通过样本数据准确估计总体数据
_21?????????è?????(www.21cnjy.com)_
