16.3 分式方程的应用
文档属性
| 名称 | 16.3 分式方程的应用 |  | |
| 格式 | zip | ||
| 文件大小 | 895.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-23 10:31:11 | ||
图片预览






文档简介
(共26张PPT)
分式方程的应用
16.3 分式方程
教学目标:
1、用列表法列分式方程、
解决现实情境中的问题。
2、体会数学模型的应用价值。
教学重点:利用列表法审明题意,
将实际问题转化为分式方程的数学模型。
教学难点:从有形的列表逐渐过渡到无形的列表
(脑中理清题意)找准等量关系。
2、在行程问题中,主要是有三个量---路程、速度、时间。它们的关系是----
路程= 、速度= 、时间= 。
3、在水流行程中:已知静水速度和水流速度
顺水速度= ,
逆水速度= 。
速度×时间
静水速度 + 水流速度
静水速度-水流速度
1、在工程问题中,主要的三个量是:工作量、工作效率、工作时间。它们的关系是
工作量=________________、工作效率=_________
工作时间=_________
工作效率×工作时间
1、填空复习
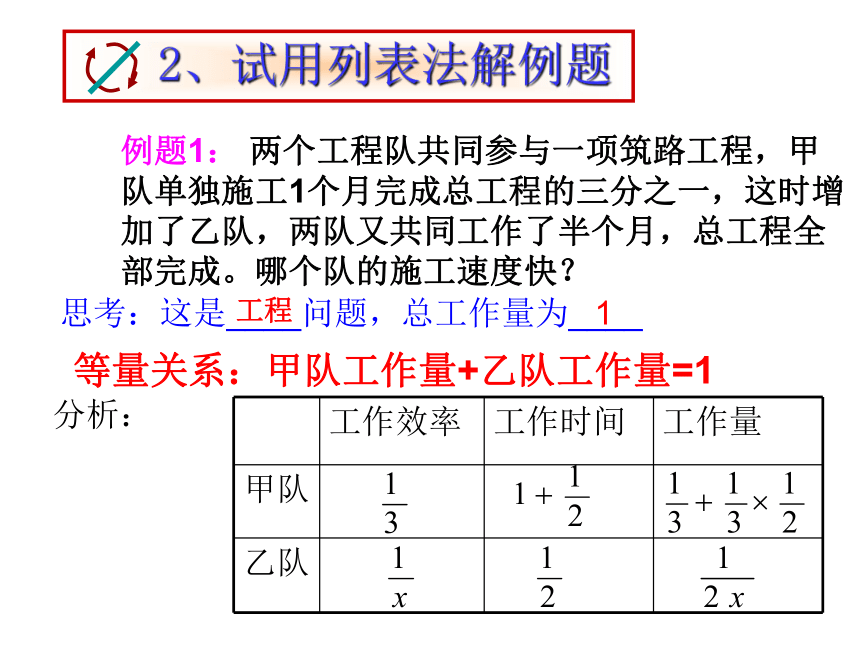
例题1: 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
工作效率 工作时间 工作量
甲队
乙队
思考:这是____问题,总工作量为____
分析:
等量关系:甲队工作量+乙队工作量=1
工程
1
2、试用列表法解例题
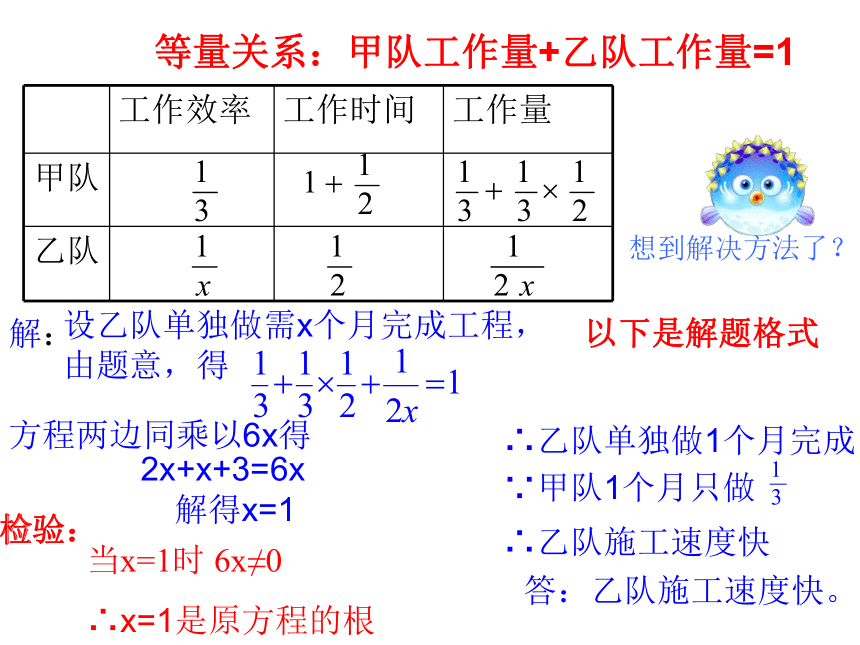
等量关系:甲队工作量+乙队工作量=1
解:
设乙队单独做需x个月完成工程,由题意,得
解得x=1
当x=1时 6x≠0
∴x=1是原方程的根
答:乙队施工速度快。
∴乙队单独做1个月完成
∵甲队1个月只做
∴乙队施工速度快
想到解决方法了?
以下是解题格式
工作效率 工作时间 工作量
甲队
乙队
方程两边同乘以6x得
2x+x+3=6x
检验:
例题2:从2004年5月起某列车平均提速v千米/小时,用相同的时间,列车提速前行驶s千米,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?
路程km 速度km/h 时间h
提速前
提速后
思考:这是____问题
行程
等量关系:时间相等
2、试用列表法解例题
路程km 速度km/h 时间h
提速前
提速后
等量关系:时间相等
解:
设提速前列车的平均速度为x千米/时由题意,得
解得x=
答:提速前列车的平均速度为 千米/时。
注意:
s、v的实际意义
以下是解题格式
在方程两边同乘以x(x+v)得:
s(x+v)=x(s+50)
检验:当x= 时,x(x+v)≠0
∴x= 是原方程的根
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.且答案要生活化.
3、随时小结
两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
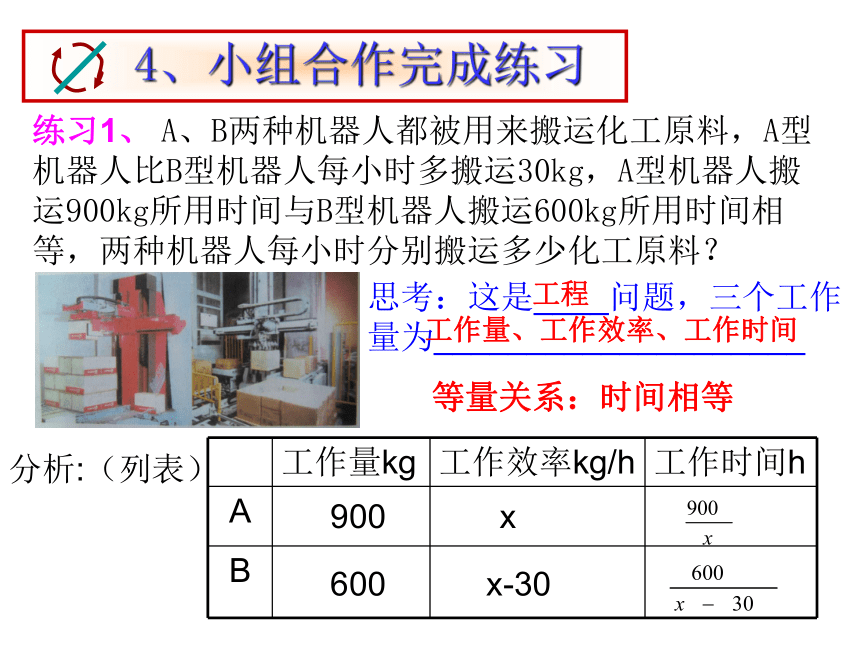
练习1、 A、B两种机器人都被用来搬运化工原料,A型 机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
分析:(列表)
工作量kg 工作效率kg/h 工作时间h
A
B
900
600
x
x-30
等量关系:时间相等
思考:这是____问题,三个工作量为____________________
工程
工作量、工作效率、工作时间
4、小组合作完成练习
解:
等量关系:时间相等
设A种机器人每小时搬运x kg,由题意得
=
解得x=90
检验:当x=90时,x(x-30)≠0
∴ x=90是原方程的根
∴ x-30=60
答:A和B两种机器人每小时分别能搬90kg和60kg。
工作量kg 工作效率kg/h 工作时间h
A
B
900
600
x
x-30
以下是解题格式
在方程两边都乘以x(x-30)得
900(x-30)=600x
练习2、某工程队需要在规定日期内完成。若甲队单独做正好按时完成;若乙队单独做,超过规定日期三天才能完成。现由甲、乙合作两天,余下工程由乙队单独做,恰好按期完成,问规定日期是多少天?
工作效率 工作时间 完成的工作量
甲
乙
思考:这是____问题
工程
等量关系:甲完成的工作量+乙完成的工作量=总工作量
4、小组合作完成练习
工作效率 工作时间 完成的工作量
甲
乙
等量关系:
甲完成的工作量+乙完成的工作量=总做总量
解:
设规定日期是x天,由题意,得
解得x=
答:规定日期是6天。
以下是解题格式
检验:当x=6时,x(x+3)≠0
∴ x=6是原方程的根
在方程两边都乘以x(x+3)得:
2(x+3)+x=x(x+3)
练习3、八年级学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了20分后,其余同学乘汽车出发,结果他们同时到达。已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度。
路程km 速度km/h 时间h
骑自行车者
乘汽车者
10
10
x
2x
思考:这是____问题,三个量
为____________________
行程
路程、速度、时间
等量关系:
骑自行车的时间-乘汽车的时间=20分= 小时
4、小组合作完成练习
路程km 速度km/h 时间h
骑自行车者
乘汽车者
10
10
x
2x
解:
设骑车同学的速度为x千米/时,由题意,得
解得x=15
答:骑车同学的速度为15千米/时。
以下是解题格式
等量关系:
骑自行车的时间-乘汽车的时间=20分= 小时
检验:当x=15时,2x≠0
∴ x=15是原方程的根
在方程两边都乘以2x得:
60-30=2x
练习4、甲、乙两人分别从相距目的地6千米和10千米的两地同时出发,甲、乙的速度比是3:4,结果甲比乙提前20分到达目的地。求甲、乙的速度。
速度(千米/时) 路程(千米) 时间(时)
甲
乙
3x
4x
6
10
思考:这是____问题,三个工作量为____________________
行程
路程、速度、时间
4、小组合作完成练习
等量关系:乙用的时间-甲用的时间=20分钟= 小时
解:
设甲的速度x千米/时,则乙的速度是3x千米/时由题意得
解得x=1.5
答:甲的速度4.5千米/时,乙的速度是6千米/时。
以下是解题格式
速度(千米/时) 路程(千米) 时间(时)
甲
乙
3x
4x
6
10
等量关系:乙用的时间-甲用的时间=20分钟= 小时
∴ 3x=4.5 ,4x=6
检验:当x=1.5时,12x≠0
∴ x=1.5是原方程的根
在方程两边都乘以12x得:
30-24=4x
练习5、一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水,向容器中注满水的全过程共用时间t分。求两根水管各自的注水速度。 (提示:要考虑大水管的进水速度是小水管进水速度的多少倍)
思考:这是____问题,三个量
为____________________
工程
工作量、工作效率、工作时间
4、小组合作完成练习
完成的工作量(立方米) 工作效率(立方米/分) 工作时间(分)
小水管
大水管
等量关系:小水管注水时间+大水管注水时间=t分
大水管口径是小水管的2倍,则大水管的截面积是小水管的4倍,那么大水管的进水速度是小水管的4倍。
大水管的进水速度是小水管的4倍。
完成的工作量(立方米) 工作效率(立方米/分) 工作时间(分)
小水管
大水管
等量关系:小水管注水时间+大水管注水时间=t分
解:
设小水管注水的速度x立方米/分,则大水管注水的速度4x立方米/分,由题意得
∴解得x=
以下是解题格式
∴ 4x= 。
8tx=5v
∵8t≠0
答:小水管的速度 立方米/分, 大水管的速度 立方米/分。
在方程两边都乘以8x得:
检验:当x= 时,12x≠0
∴ x= 是原方程的根
等量关系:
第二组用的时间-第一组用的时间=15分钟
练习6、两个小组同时开始攀登一座450米高的山,第一组的速度是第二组的1.2倍,他们比第二组早15分到达顶峰,两个小组的速度各是多少? (若山高h米,第一组的速度是第二组的a倍,并比第二组早t分到达顶峰,则两组速度各是多少?)
速度(米/分) 路程(米) 时间(分)
第一组
第二组
1.2x
x
450
450
思考:这是____问题,三个工作量为____________________
行程
路程、速度、时间
4、小组合作完成练习
解:
设第二组的速度x米/分,则第一组的速度是1.2x米/分由题意得
解得x=5
答:第一组的速度6米/分,第二组的速度是5米/分。
以下是解题格式
∴ 1.2x=6
速度(米/分) 路程(米) 时间(分)
第一组
第二组
1.2x
x
450
450
等量关系:
第二组用的时间-第一组用的时间=15分钟
检验:当x=5时,12x≠0
∴ x=5是原方程的根
在方程两边都乘以12x得:
5400-4500=180x
等量关系:
第二组用的时间-第一组用的时间=t分钟
练习6、两个小组同时开始攀登一座450米高的山,第一组的速度是第二组的1.2倍,他们比第二组早15分到达顶峰,两个小组的速度各是多少? (若山高h米,第一组的速度是第二组的a倍,并比第二组早t分到达顶峰,则两组速度各是多少?)
速度(米/分) 路程(米) 时间(分)
第一组
第二组
ax
x
h
h
思考:这是____问题,三个工作量为____________________
行程
路程、速度、时间
4、小组合作完成练习
解:
设第二组的速度x米/分,则第一组的速度是ax米/分由题意得
∴解得x=
以下是解题格式
∴ ax=
速度(米/分) 路程(米) 时间(分)
第一组
第二组
ax
x
h
h
等量关系:
第二组用的时间-第一组用的时间=t分钟
∵at≠0
答:第一组的速度 米/分,第二组的速度是 米/分。
ah-h=atx
在方程两边都乘以ax得:
检验:当x= 时,ax≠0
∴ x= 是原方程的根
2、老师小结:列表法可以方便理解解应用题。列表是一种手段而不是目的,平常做应用题可在心中自有一张表格,逐项理清,而不必都要列在纸上。
1、学生小结(心情、知识点、疑惑处等)
教师寄语
见课本:P32 第5、6题
分式方程的应用
16.3 分式方程
教学目标:
1、用列表法列分式方程、
解决现实情境中的问题。
2、体会数学模型的应用价值。
教学重点:利用列表法审明题意,
将实际问题转化为分式方程的数学模型。
教学难点:从有形的列表逐渐过渡到无形的列表
(脑中理清题意)找准等量关系。
2、在行程问题中,主要是有三个量---路程、速度、时间。它们的关系是----
路程= 、速度= 、时间= 。
3、在水流行程中:已知静水速度和水流速度
顺水速度= ,
逆水速度= 。
速度×时间
静水速度 + 水流速度
静水速度-水流速度
1、在工程问题中,主要的三个量是:工作量、工作效率、工作时间。它们的关系是
工作量=________________、工作效率=_________
工作时间=_________
工作效率×工作时间
1、填空复习
例题1: 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
工作效率 工作时间 工作量
甲队
乙队
思考:这是____问题,总工作量为____
分析:
等量关系:甲队工作量+乙队工作量=1
工程
1
2、试用列表法解例题
等量关系:甲队工作量+乙队工作量=1
解:
设乙队单独做需x个月完成工程,由题意,得
解得x=1
当x=1时 6x≠0
∴x=1是原方程的根
答:乙队施工速度快。
∴乙队单独做1个月完成
∵甲队1个月只做
∴乙队施工速度快
想到解决方法了?
以下是解题格式
工作效率 工作时间 工作量
甲队
乙队
方程两边同乘以6x得
2x+x+3=6x
检验:
例题2:从2004年5月起某列车平均提速v千米/小时,用相同的时间,列车提速前行驶s千米,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?
路程km 速度km/h 时间h
提速前
提速后
思考:这是____问题
行程
等量关系:时间相等
2、试用列表法解例题
路程km 速度km/h 时间h
提速前
提速后
等量关系:时间相等
解:
设提速前列车的平均速度为x千米/时由题意,得
解得x=
答:提速前列车的平均速度为 千米/时。
注意:
s、v的实际意义
以下是解题格式
在方程两边同乘以x(x+v)得:
s(x+v)=x(s+50)
检验:当x= 时,x(x+v)≠0
∴x= 是原方程的根
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.且答案要生活化.
3、随时小结
两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
练习1、 A、B两种机器人都被用来搬运化工原料,A型 机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
分析:(列表)
工作量kg 工作效率kg/h 工作时间h
A
B
900
600
x
x-30
等量关系:时间相等
思考:这是____问题,三个工作量为____________________
工程
工作量、工作效率、工作时间
4、小组合作完成练习
解:
等量关系:时间相等
设A种机器人每小时搬运x kg,由题意得
=
解得x=90
检验:当x=90时,x(x-30)≠0
∴ x=90是原方程的根
∴ x-30=60
答:A和B两种机器人每小时分别能搬90kg和60kg。
工作量kg 工作效率kg/h 工作时间h
A
B
900
600
x
x-30
以下是解题格式
在方程两边都乘以x(x-30)得
900(x-30)=600x
练习2、某工程队需要在规定日期内完成。若甲队单独做正好按时完成;若乙队单独做,超过规定日期三天才能完成。现由甲、乙合作两天,余下工程由乙队单独做,恰好按期完成,问规定日期是多少天?
工作效率 工作时间 完成的工作量
甲
乙
思考:这是____问题
工程
等量关系:甲完成的工作量+乙完成的工作量=总工作量
4、小组合作完成练习
工作效率 工作时间 完成的工作量
甲
乙
等量关系:
甲完成的工作量+乙完成的工作量=总做总量
解:
设规定日期是x天,由题意,得
解得x=
答:规定日期是6天。
以下是解题格式
检验:当x=6时,x(x+3)≠0
∴ x=6是原方程的根
在方程两边都乘以x(x+3)得:
2(x+3)+x=x(x+3)
练习3、八年级学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了20分后,其余同学乘汽车出发,结果他们同时到达。已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度。
路程km 速度km/h 时间h
骑自行车者
乘汽车者
10
10
x
2x
思考:这是____问题,三个量
为____________________
行程
路程、速度、时间
等量关系:
骑自行车的时间-乘汽车的时间=20分= 小时
4、小组合作完成练习
路程km 速度km/h 时间h
骑自行车者
乘汽车者
10
10
x
2x
解:
设骑车同学的速度为x千米/时,由题意,得
解得x=15
答:骑车同学的速度为15千米/时。
以下是解题格式
等量关系:
骑自行车的时间-乘汽车的时间=20分= 小时
检验:当x=15时,2x≠0
∴ x=15是原方程的根
在方程两边都乘以2x得:
60-30=2x
练习4、甲、乙两人分别从相距目的地6千米和10千米的两地同时出发,甲、乙的速度比是3:4,结果甲比乙提前20分到达目的地。求甲、乙的速度。
速度(千米/时) 路程(千米) 时间(时)
甲
乙
3x
4x
6
10
思考:这是____问题,三个工作量为____________________
行程
路程、速度、时间
4、小组合作完成练习
等量关系:乙用的时间-甲用的时间=20分钟= 小时
解:
设甲的速度x千米/时,则乙的速度是3x千米/时由题意得
解得x=1.5
答:甲的速度4.5千米/时,乙的速度是6千米/时。
以下是解题格式
速度(千米/时) 路程(千米) 时间(时)
甲
乙
3x
4x
6
10
等量关系:乙用的时间-甲用的时间=20分钟= 小时
∴ 3x=4.5 ,4x=6
检验:当x=1.5时,12x≠0
∴ x=1.5是原方程的根
在方程两边都乘以12x得:
30-24=4x
练习5、一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水,向容器中注满水的全过程共用时间t分。求两根水管各自的注水速度。 (提示:要考虑大水管的进水速度是小水管进水速度的多少倍)
思考:这是____问题,三个量
为____________________
工程
工作量、工作效率、工作时间
4、小组合作完成练习
完成的工作量(立方米) 工作效率(立方米/分) 工作时间(分)
小水管
大水管
等量关系:小水管注水时间+大水管注水时间=t分
大水管口径是小水管的2倍,则大水管的截面积是小水管的4倍,那么大水管的进水速度是小水管的4倍。
大水管的进水速度是小水管的4倍。
完成的工作量(立方米) 工作效率(立方米/分) 工作时间(分)
小水管
大水管
等量关系:小水管注水时间+大水管注水时间=t分
解:
设小水管注水的速度x立方米/分,则大水管注水的速度4x立方米/分,由题意得
∴解得x=
以下是解题格式
∴ 4x= 。
8tx=5v
∵8t≠0
答:小水管的速度 立方米/分, 大水管的速度 立方米/分。
在方程两边都乘以8x得:
检验:当x= 时,12x≠0
∴ x= 是原方程的根
等量关系:
第二组用的时间-第一组用的时间=15分钟
练习6、两个小组同时开始攀登一座450米高的山,第一组的速度是第二组的1.2倍,他们比第二组早15分到达顶峰,两个小组的速度各是多少? (若山高h米,第一组的速度是第二组的a倍,并比第二组早t分到达顶峰,则两组速度各是多少?)
速度(米/分) 路程(米) 时间(分)
第一组
第二组
1.2x
x
450
450
思考:这是____问题,三个工作量为____________________
行程
路程、速度、时间
4、小组合作完成练习
解:
设第二组的速度x米/分,则第一组的速度是1.2x米/分由题意得
解得x=5
答:第一组的速度6米/分,第二组的速度是5米/分。
以下是解题格式
∴ 1.2x=6
速度(米/分) 路程(米) 时间(分)
第一组
第二组
1.2x
x
450
450
等量关系:
第二组用的时间-第一组用的时间=15分钟
检验:当x=5时,12x≠0
∴ x=5是原方程的根
在方程两边都乘以12x得:
5400-4500=180x
等量关系:
第二组用的时间-第一组用的时间=t分钟
练习6、两个小组同时开始攀登一座450米高的山,第一组的速度是第二组的1.2倍,他们比第二组早15分到达顶峰,两个小组的速度各是多少? (若山高h米,第一组的速度是第二组的a倍,并比第二组早t分到达顶峰,则两组速度各是多少?)
速度(米/分) 路程(米) 时间(分)
第一组
第二组
ax
x
h
h
思考:这是____问题,三个工作量为____________________
行程
路程、速度、时间
4、小组合作完成练习
解:
设第二组的速度x米/分,则第一组的速度是ax米/分由题意得
∴解得x=
以下是解题格式
∴ ax=
速度(米/分) 路程(米) 时间(分)
第一组
第二组
ax
x
h
h
等量关系:
第二组用的时间-第一组用的时间=t分钟
∵at≠0
答:第一组的速度 米/分,第二组的速度是 米/分。
ah-h=atx
在方程两边都乘以ax得:
检验:当x= 时,ax≠0
∴ x= 是原方程的根
2、老师小结:列表法可以方便理解解应用题。列表是一种手段而不是目的,平常做应用题可在心中自有一张表格,逐项理清,而不必都要列在纸上。
1、学生小结(心情、知识点、疑惑处等)
教师寄语
见课本:P32 第5、6题
