六年级下册数学教案-7.1.13 正比例和反比例整理和复习苏教版
文档属性
| 名称 | 六年级下册数学教案-7.1.13 正比例和反比例整理和复习苏教版 | 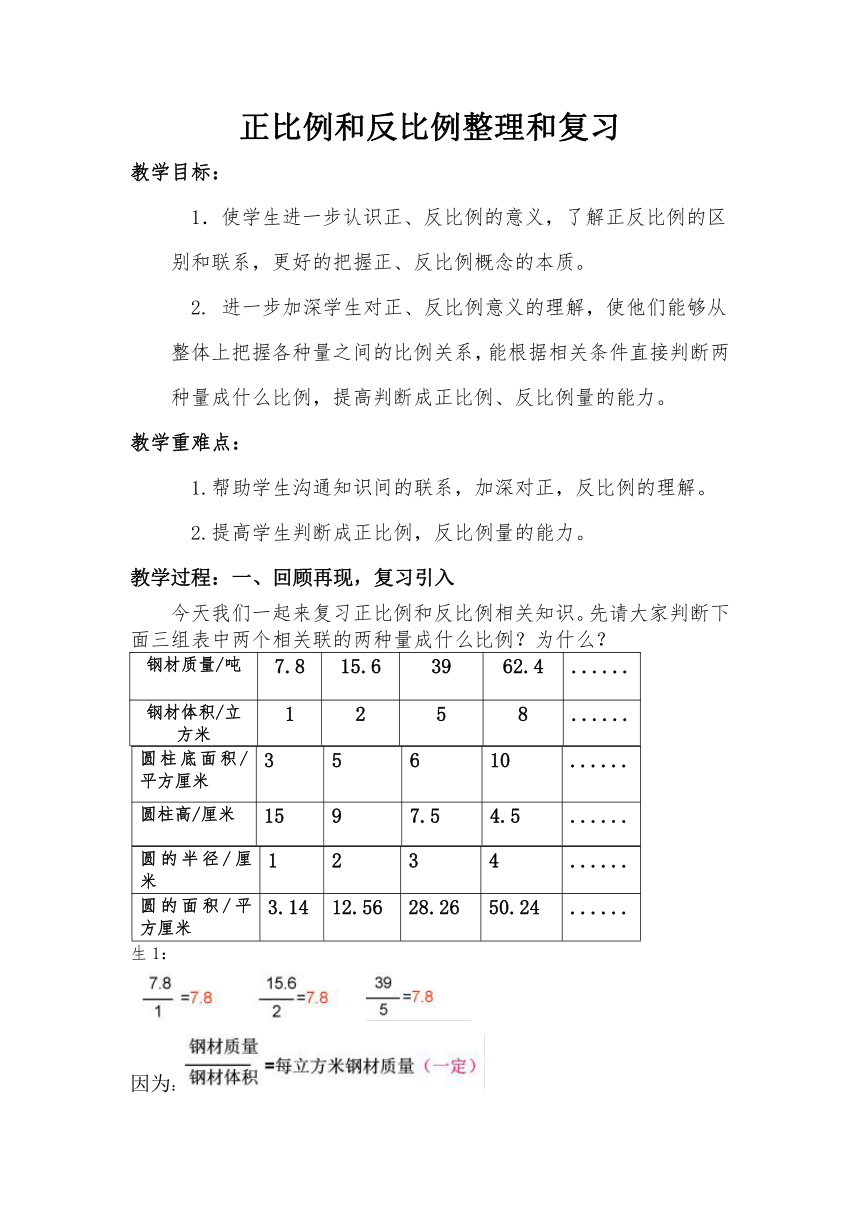 | |
| 格式 | docx | ||
| 文件大小 | 626.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 08:01:30 | ||
图片预览


文档简介
正比例和反比例整理和复习
教学目标:
1.使学生进一步认识正、反比例的意义,了解正反比例的区别和联系,更好的把握正、反比例概念的本质。
2. 进一步加深学生对正、反比例意义的理解,使他们能够从整体上把握各种量之间的比例关系,能根据相关条件直接判断两种量成什么比例,提高判断成正比例、反比例量的能力。
教学重难点:
1.帮助学生沟通知识间的联系,加深对正,反比例的理解。
2.提高学生判断成正比例,反比例量的能力。
教学过程:一、回顾再现,复习引入
今天我们一起来复习正比例和反比例相关知识。先请大家判断下面三组表中两个相关联的两种量成什么比例?为什么?
钢材质量/吨
7.8
15.6
39
62.4
......
钢材体积/立方米
1
2
5
8
......
圆柱底面积/平方厘米
3
5
6
10
......
圆柱高/厘米
15
9
7.5
4.5
......
圆的半径/厘米
1
2
3
4
......
圆的面积/平方厘米
3.14
12.56
28.26
50.24
......
生1:
因为:
(此处学生若遗漏,师补充。)
所以:钢材质量和钢材体积成正比例关系。
生2:
生3:
知识点归纳:
1.说一说,如果用χ和y表示成比例的两种相关联的量,那么什么情况下成正比例关系,什么情况下成反比例关系?
正比例关系:
Y/x=k(一定)
反比例关系:
χ×y=k(一定)
2.想一想,成正比例关系和成反比例关系的两种量有什么相同点和不同点?
3.怎样判断两种量是否成正比例或反比例关系?
学生交流
练习与实践
1.
生1:
生2:
2.完成“练习与实践”第9题
第1小题让学生根据图中标出的点的位置算出相应的耗油量与行驶路程的比值,再作判断。(行驶75千米的耗油量是6升。)
第2小题让学生在教材提供的方格图上描点、连线,
引导学生联系画出的图象判断汽车在市区行驶时,行驶的路程与耗油量成不成正比例。体会数形结合在解决问题方面的价值。(投影学生作业)
3、在数量、单价和总价
(1)如果 一定, 和 成正比例。
(2)如果 一定, 和 成正比例。
(3)如果 一定, 和 成反比例
4. 如果x=3y ,那么x和y成( )比例;
如果4x=5y,那么x和y( )比例。
如果 8÷X =Y,所以X与Y( )。
如果ab+3=12,则a与b成( )比例
5.完成部分课堂练习。
四.全课小结:
通过学习你有什么收获?
教学目标:
1.使学生进一步认识正、反比例的意义,了解正反比例的区别和联系,更好的把握正、反比例概念的本质。
2. 进一步加深学生对正、反比例意义的理解,使他们能够从整体上把握各种量之间的比例关系,能根据相关条件直接判断两种量成什么比例,提高判断成正比例、反比例量的能力。
教学重难点:
1.帮助学生沟通知识间的联系,加深对正,反比例的理解。
2.提高学生判断成正比例,反比例量的能力。
教学过程:一、回顾再现,复习引入
今天我们一起来复习正比例和反比例相关知识。先请大家判断下面三组表中两个相关联的两种量成什么比例?为什么?
钢材质量/吨
7.8
15.6
39
62.4
......
钢材体积/立方米
1
2
5
8
......
圆柱底面积/平方厘米
3
5
6
10
......
圆柱高/厘米
15
9
7.5
4.5
......
圆的半径/厘米
1
2
3
4
......
圆的面积/平方厘米
3.14
12.56
28.26
50.24
......
生1:
因为:
(此处学生若遗漏,师补充。)
所以:钢材质量和钢材体积成正比例关系。
生2:
生3:
知识点归纳:
1.说一说,如果用χ和y表示成比例的两种相关联的量,那么什么情况下成正比例关系,什么情况下成反比例关系?
正比例关系:
Y/x=k(一定)
反比例关系:
χ×y=k(一定)
2.想一想,成正比例关系和成反比例关系的两种量有什么相同点和不同点?
3.怎样判断两种量是否成正比例或反比例关系?
学生交流
练习与实践
1.
生1:
生2:
2.完成“练习与实践”第9题
第1小题让学生根据图中标出的点的位置算出相应的耗油量与行驶路程的比值,再作判断。(行驶75千米的耗油量是6升。)
第2小题让学生在教材提供的方格图上描点、连线,
引导学生联系画出的图象判断汽车在市区行驶时,行驶的路程与耗油量成不成正比例。体会数形结合在解决问题方面的价值。(投影学生作业)
3、在数量、单价和总价
(1)如果 一定, 和 成正比例。
(2)如果 一定, 和 成正比例。
(3)如果 一定, 和 成反比例
4. 如果x=3y ,那么x和y成( )比例;
如果4x=5y,那么x和y( )比例。
如果 8÷X =Y,所以X与Y( )。
如果ab+3=12,则a与b成( )比例
5.完成部分课堂练习。
四.全课小结:
通过学习你有什么收获?
