2020--2021年度人教版八年级数学下册第十七章勾股定理单元同步检测试题(Word版,含答案)
文档属性
| 名称 | 2020--2021年度人教版八年级数学下册第十七章勾股定理单元同步检测试题(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 176.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-20 17:31:57 | ||
图片预览



文档简介
第十七章《勾股定理》单元检测题
题号
一
二
三
总分
17
18
19
20
21
分数
一、选择题(每小题3分,共30分)
1.下列各组数中,不是勾股数的为( )
A.3,4,5
B.6,8,10
C.5,12,13
D.5,7,10
2.若△ABC满足下列条件,则能判断其为直角三角形的选项有( )个.
(1)∠A=∠B﹣∠C.(2)∠A:∠B:∠C=1:1:2.(3)a:b:c=1:1:2.(4)b2=a2﹣c2
A.1
B.2
C.3
D.4
3.若△ABC的三边a、b、c满足(a﹣b)2+|a2+b2﹣c2|=0,则△ABC是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
4.如图,在Rt△ABC中,∠BAC=90°.ED是BC的垂直平分线,BD平分∠ABC,AD=3.则CD的长为( )
A.6
B.5
C.4
D.3
5.如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( )
A.75
B.100
C.120
D.125
6.若的三边长a、b、c满足,那么是(
)
A.等腰三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
7.已知一个直角三角形的两边长分别为1和2,则第三边长是(
)
A.3
B.
C.
D.或
8.已知,等边三角形ΔABC中,边长为2,则面积为(
)
A.1
B.2
C.
D.
9.如图,在Rt△ABC中,∠ACB=90°,AE为△ABC的角平分线,且ED⊥AB,若AC=6,BC=8,则BD的长( )
A.2
B.3
C.4
D.5
10.如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49;②x﹣y=2;③x+y=;④2xy+4=49;其中说法正确的是( )
A.①②
B.①②③
C.①②④
D.①②③④
二、填空题(每小题4分,共24分)
11.已知一个直角三角形的两条直角边长分别为5cm、12cm,那么第三条斜边的长是
_________.
12.已知△ABC的三边长分别是6,8,10,则△ABC的面积是__________.
13.若一个三角形的三边长a,b,c满足(a+b)2=c2+2ab,则这个三角形的形状是________.
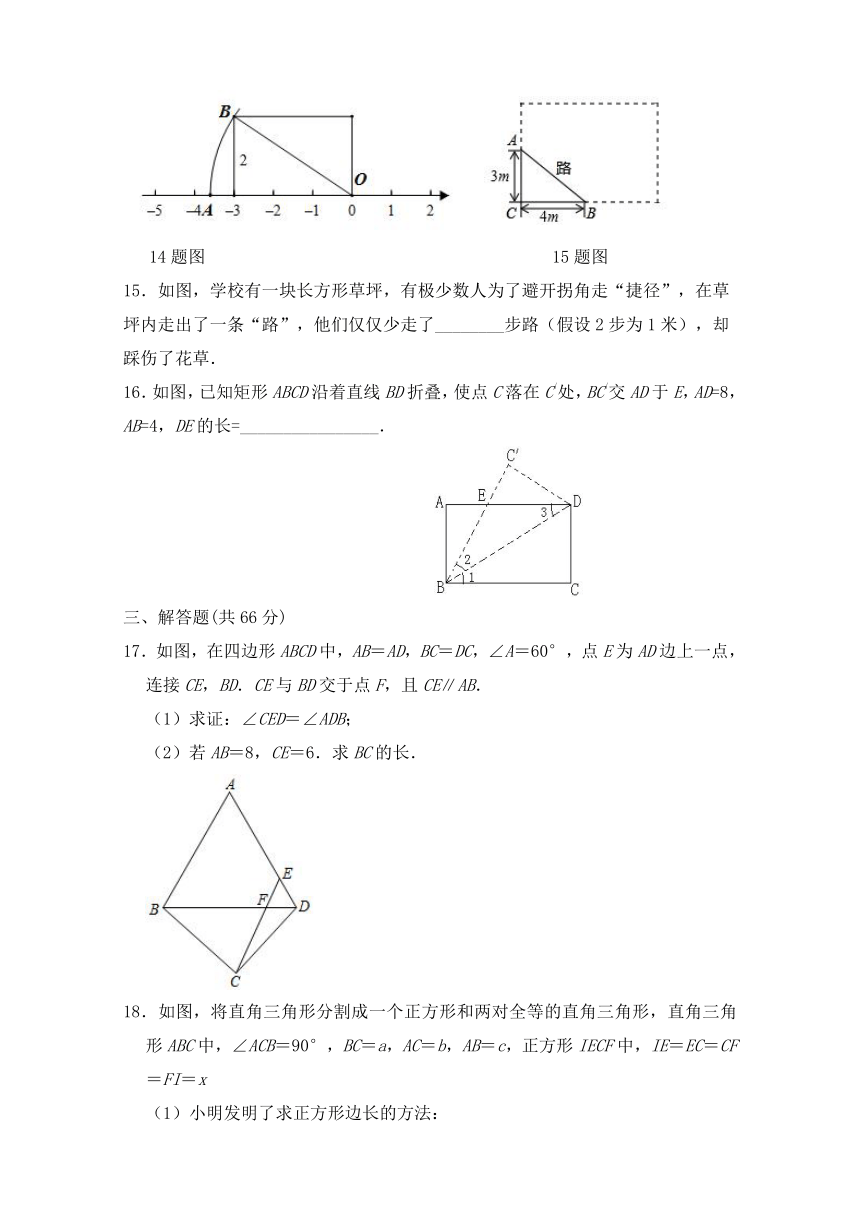
14.如图,已知OA=OB,数轴上点A对应的数是______.
14题图
15题图
15.如图,学校有一块长方形草坪,有极少数人为了避开拐角走“捷径”,在草坪内走出了一条“路”,他们仅仅少走了________步路(假设2步为1米),却踩伤了花草.
16.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C/处,BC/交AD于E,AD=8,AB=4,DE的长=________________.
三、解答题(共66分)
17.如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,点E为AD边上一点,连接CE,BD.CE与BD交于点F,且CE∥AB.
(1)求证:∠CED=∠ADB;
(2)若AB=8,CE=6.求BC的长.
18.如图,将直角三角形分割成一个正方形和两对全等的直角三角形,直角三角形ABC中,∠ACB=90°,BC=a,AC=b,AB=c,正方形IECF中,IE=EC=CF=FI=x
(1)小明发明了求正方形边长的方法:
由题意可得BD=BE=a﹣x,AD=AF=b﹣x
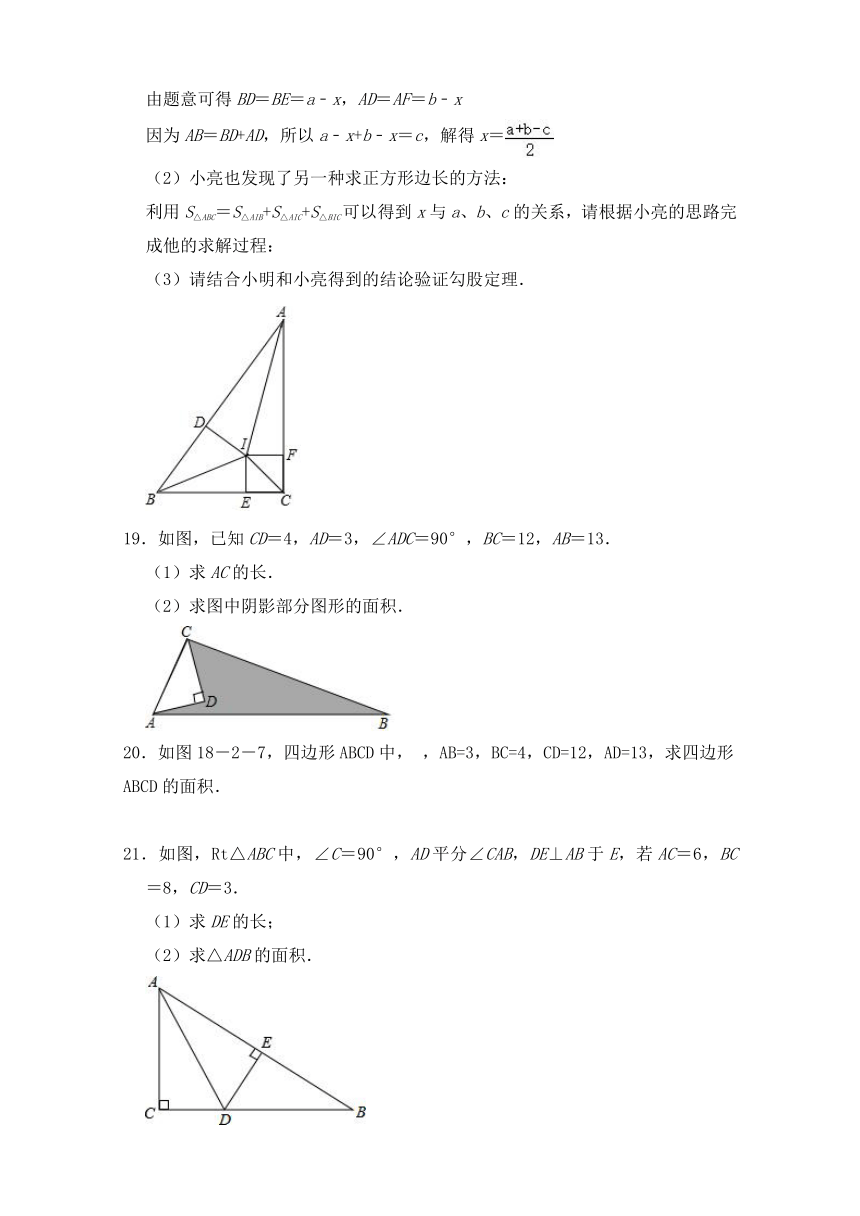
因为AB=BD+AD,所以a﹣x+b﹣x=c,解得x=
(2)小亮也发现了另一种求正方形边长的方法:
利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系,请根据小亮的思路完成他的求解过程:
(3)请结合小明和小亮得到的结论验证勾股定理.
19.如图,已知CD=4,AD=3,∠ADC=90°,BC=12,AB=13.
(1)求AC的长.
(2)求图中阴影部分图形的面积.
20.如图18-2-7,四边形ABCD中,
,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
21.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积.
22.如图,已知AB=12;AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,求AE的长.
23.如图,在△ABC中,∠ACB=90°,BC=15,AC=20,CD是高.
(1)求AB的长;
(2)求△ABC的面积;
(3)求CD的长.
参考答案
一、选择题
1.D
2.
C
3.
C
4.
A
5.
A
6.
B
7.
D
8.D
9.
C
10.D
二、填空题
11.13㎝
12.24
13.直角三角形.
14.-.
解析:由勾股定理得
∵OA=OB,∴OA=,∴数轴上点A对应的数是-
.
故答案为:-.
15.4.
解析:如图,
∵在Rt△ABC中,AB2=AC2+BC2,
∴
,
则少走的距离为:AC+BC-AB=3+4-5=2(m),
∵2步为1米,∴少走了4步.故答案为:4.
16.
5.
解析:∵四边形ABCD是矩形,∴AD∥BC,即∠1=∠3,
由折叠知,∠1=∠2,
C′D=CD=4、BC′=BC=8,∴∠2=∠3,即DE=BE,
设DE=x,则EC′=8?x,在Rt△DEC′中,DC′2+EC′2=DE2
∴42+(8?x)2=x2解得:x=5,∴DE的长为5.
三、解答题:
17.
【解答】(1)证明:∵AB=AD,∠A=60°,
∴△ABD是等边三角形.
∴∠ADB=60°,
∵CE∥AB,
∴∠CED=∠A=60°,
∴∠CED=∠ADB.
(2)解:连接AC交BD于点O,
∵AB=AD,BC=DC,
∴AC垂直平分BD.
∴∠BAO=∠DAO=30°.
∵△ABD是等边三角形,AB=8,
∴AD=BD=AB=8,
∴BO=OD=4,
∵CE∥AB,
∴∠ACE=∠BAO.
∴AE=CE=6,DE=AD﹣AE=2.
∵∠CED=∠ADB=60°.
∴∠EFD=60°.
∴△EDF是等边三角形.
∴EF=DF=DE=2,
∴CF=CE﹣EF=4,OF=OD﹣DF=2.
在Rt△COF中,
∴,
在Rt△BOC中,
∴.
18.
【解答】解:(2)因为S△ABC=S△ABI+S△BIC+S△AIC
=cx+ax+bx
所以x=.
答:x与a、b、c的关系为x=.
(3)根据(1)和(2)得:
x==.
即2ab=(a+b+c)(a+b﹣c)
化简得a2+b2=c2.
19.
【解答】解:(1)在Rt△ADC中,∠ADC=90°,
由勾股定理,得:AC===5;
(2)∵AC2+BC2=52+122=132=AB2,
∴△ABC是直角三角形,
∴图中阴影部分图形的面积=S△ABC﹣S△ACD=×5×12﹣×3×4=30﹣6=24.
20.连接AC,得
,由勾股定理知AC=5,
AC2+CD2=52+122=169=132=AD2,
ACD=
S四边形ABCD=S
ABC+S
ACD=
=
6+30=36.
21.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积.
【分析】(1)根据角平分线的性质得到CD=DE;
(2)根据勾股定理求出AB,根据三角形的面积公式计算.
【解答】解:(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=DE,
∵CD=3,
∴DE=3;
(2)在Rt△ABC中,∠C=90°,AC=6,BC=8,
由勾股定理,得AB═10,
∴△ADB的面积为S=AB?DE=×10×3=15.
22.如图,已知AB=12;AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,求AE的长.
【分析】如图,延长AE交BC于F,构造全等三角形△AED≌△FEC(AAS),则对应边AE=FE,AD=FC.在Rt△ABF中,利用勾股定理即可求得线段AF的长度.
【解答】解:如图,延长AE交BC于F.
∵AB⊥BC,AB⊥AD,
∴AD∥BC
∴∠D=∠C,∠DAE=∠CFE,
又∵点E是CD的中点,
∴DE=CE.
∵在△AED与△FEC中,
,
∴△AED≌△FEC(AAS),
∴AE=FE,AD=FC.
∵AD=5,BC=10.
∴BF=5
在Rt△ABF中,,
∴AE=AF=6.5.
23.如图,在△ABC中,∠ACB=90°,BC=15,AC=20,CD是高.
(1)求AB的长;
(2)求△ABC的面积;
(3)求CD的长.
【分析】(1)根据勾股定理可求得AB的长;
(2)根据三角形的面积公式计算即可求解;
(3)根据三角形的面积相等即可求得CD的长.
【解答】解:(1)∵在△ABC中,∠ACB=90°,BC=15,AC=20,
∴AB2=AC2+BC2,
解得AB=25.
答:AB的长是25;
(2)AC?BC=×20×15=150.
答:△ABC的面积是150;
(3)∵CD是边AB上的高,
∴AC?BC=AB?CD,
解得:CD=12.
答:CD的长是12.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
题号
一
二
三
总分
17
18
19
20
21
分数
一、选择题(每小题3分,共30分)
1.下列各组数中,不是勾股数的为( )
A.3,4,5
B.6,8,10
C.5,12,13
D.5,7,10
2.若△ABC满足下列条件,则能判断其为直角三角形的选项有( )个.
(1)∠A=∠B﹣∠C.(2)∠A:∠B:∠C=1:1:2.(3)a:b:c=1:1:2.(4)b2=a2﹣c2
A.1
B.2
C.3
D.4
3.若△ABC的三边a、b、c满足(a﹣b)2+|a2+b2﹣c2|=0,则△ABC是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
4.如图,在Rt△ABC中,∠BAC=90°.ED是BC的垂直平分线,BD平分∠ABC,AD=3.则CD的长为( )
A.6
B.5
C.4
D.3
5.如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( )
A.75
B.100
C.120
D.125
6.若的三边长a、b、c满足,那么是(
)
A.等腰三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
7.已知一个直角三角形的两边长分别为1和2,则第三边长是(
)
A.3
B.
C.
D.或
8.已知,等边三角形ΔABC中,边长为2,则面积为(
)
A.1
B.2
C.
D.
9.如图,在Rt△ABC中,∠ACB=90°,AE为△ABC的角平分线,且ED⊥AB,若AC=6,BC=8,则BD的长( )
A.2
B.3
C.4
D.5
10.如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49;②x﹣y=2;③x+y=;④2xy+4=49;其中说法正确的是( )
A.①②
B.①②③
C.①②④
D.①②③④
二、填空题(每小题4分,共24分)
11.已知一个直角三角形的两条直角边长分别为5cm、12cm,那么第三条斜边的长是
_________.
12.已知△ABC的三边长分别是6,8,10,则△ABC的面积是__________.
13.若一个三角形的三边长a,b,c满足(a+b)2=c2+2ab,则这个三角形的形状是________.
14.如图,已知OA=OB,数轴上点A对应的数是______.
14题图
15题图
15.如图,学校有一块长方形草坪,有极少数人为了避开拐角走“捷径”,在草坪内走出了一条“路”,他们仅仅少走了________步路(假设2步为1米),却踩伤了花草.
16.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C/处,BC/交AD于E,AD=8,AB=4,DE的长=________________.
三、解答题(共66分)
17.如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,点E为AD边上一点,连接CE,BD.CE与BD交于点F,且CE∥AB.
(1)求证:∠CED=∠ADB;
(2)若AB=8,CE=6.求BC的长.
18.如图,将直角三角形分割成一个正方形和两对全等的直角三角形,直角三角形ABC中,∠ACB=90°,BC=a,AC=b,AB=c,正方形IECF中,IE=EC=CF=FI=x
(1)小明发明了求正方形边长的方法:
由题意可得BD=BE=a﹣x,AD=AF=b﹣x
因为AB=BD+AD,所以a﹣x+b﹣x=c,解得x=
(2)小亮也发现了另一种求正方形边长的方法:
利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系,请根据小亮的思路完成他的求解过程:
(3)请结合小明和小亮得到的结论验证勾股定理.
19.如图,已知CD=4,AD=3,∠ADC=90°,BC=12,AB=13.
(1)求AC的长.
(2)求图中阴影部分图形的面积.
20.如图18-2-7,四边形ABCD中,
,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
21.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积.
22.如图,已知AB=12;AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,求AE的长.
23.如图,在△ABC中,∠ACB=90°,BC=15,AC=20,CD是高.
(1)求AB的长;
(2)求△ABC的面积;
(3)求CD的长.
参考答案
一、选择题
1.D
2.
C
3.
C
4.
A
5.
A
6.
B
7.
D
8.D
9.
C
10.D
二、填空题
11.13㎝
12.24
13.直角三角形.
14.-.
解析:由勾股定理得
∵OA=OB,∴OA=,∴数轴上点A对应的数是-
.
故答案为:-.
15.4.
解析:如图,
∵在Rt△ABC中,AB2=AC2+BC2,
∴
,
则少走的距离为:AC+BC-AB=3+4-5=2(m),
∵2步为1米,∴少走了4步.故答案为:4.
16.
5.
解析:∵四边形ABCD是矩形,∴AD∥BC,即∠1=∠3,
由折叠知,∠1=∠2,
C′D=CD=4、BC′=BC=8,∴∠2=∠3,即DE=BE,
设DE=x,则EC′=8?x,在Rt△DEC′中,DC′2+EC′2=DE2
∴42+(8?x)2=x2解得:x=5,∴DE的长为5.
三、解答题:
17.
【解答】(1)证明:∵AB=AD,∠A=60°,
∴△ABD是等边三角形.
∴∠ADB=60°,
∵CE∥AB,
∴∠CED=∠A=60°,
∴∠CED=∠ADB.
(2)解:连接AC交BD于点O,
∵AB=AD,BC=DC,
∴AC垂直平分BD.
∴∠BAO=∠DAO=30°.
∵△ABD是等边三角形,AB=8,
∴AD=BD=AB=8,
∴BO=OD=4,
∵CE∥AB,
∴∠ACE=∠BAO.
∴AE=CE=6,DE=AD﹣AE=2.
∵∠CED=∠ADB=60°.
∴∠EFD=60°.
∴△EDF是等边三角形.
∴EF=DF=DE=2,
∴CF=CE﹣EF=4,OF=OD﹣DF=2.
在Rt△COF中,
∴,
在Rt△BOC中,
∴.
18.
【解答】解:(2)因为S△ABC=S△ABI+S△BIC+S△AIC
=cx+ax+bx
所以x=.
答:x与a、b、c的关系为x=.
(3)根据(1)和(2)得:
x==.
即2ab=(a+b+c)(a+b﹣c)
化简得a2+b2=c2.
19.
【解答】解:(1)在Rt△ADC中,∠ADC=90°,
由勾股定理,得:AC===5;
(2)∵AC2+BC2=52+122=132=AB2,
∴△ABC是直角三角形,
∴图中阴影部分图形的面积=S△ABC﹣S△ACD=×5×12﹣×3×4=30﹣6=24.
20.连接AC,得
,由勾股定理知AC=5,
AC2+CD2=52+122=169=132=AD2,
ACD=
S四边形ABCD=S
ABC+S
ACD=
=
6+30=36.
21.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积.
【分析】(1)根据角平分线的性质得到CD=DE;
(2)根据勾股定理求出AB,根据三角形的面积公式计算.
【解答】解:(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=DE,
∵CD=3,
∴DE=3;
(2)在Rt△ABC中,∠C=90°,AC=6,BC=8,
由勾股定理,得AB═10,
∴△ADB的面积为S=AB?DE=×10×3=15.
22.如图,已知AB=12;AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,求AE的长.
【分析】如图,延长AE交BC于F,构造全等三角形△AED≌△FEC(AAS),则对应边AE=FE,AD=FC.在Rt△ABF中,利用勾股定理即可求得线段AF的长度.
【解答】解:如图,延长AE交BC于F.
∵AB⊥BC,AB⊥AD,
∴AD∥BC
∴∠D=∠C,∠DAE=∠CFE,
又∵点E是CD的中点,
∴DE=CE.
∵在△AED与△FEC中,
,
∴△AED≌△FEC(AAS),
∴AE=FE,AD=FC.
∵AD=5,BC=10.
∴BF=5
在Rt△ABF中,,
∴AE=AF=6.5.
23.如图,在△ABC中,∠ACB=90°,BC=15,AC=20,CD是高.
(1)求AB的长;
(2)求△ABC的面积;
(3)求CD的长.
【分析】(1)根据勾股定理可求得AB的长;
(2)根据三角形的面积公式计算即可求解;
(3)根据三角形的面积相等即可求得CD的长.
【解答】解:(1)∵在△ABC中,∠ACB=90°,BC=15,AC=20,
∴AB2=AC2+BC2,
解得AB=25.
答:AB的长是25;
(2)AC?BC=×20×15=150.
答:△ABC的面积是150;
(3)∵CD是边AB上的高,
∴AC?BC=AB?CD,
解得:CD=12.
答:CD的长是12.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
