鲁教版(五四制)七年级下册数学 10.1全等三角形(一) 导学案(无答案)
文档属性
| 名称 | 鲁教版(五四制)七年级下册数学 10.1全等三角形(一) 导学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 51.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-20 08:18:49 | ||
图片预览

文档简介
10.1 全等三角形(一)导学案
【学习目标】
了解作为证明基础的几条基本事实的内容,掌握证明的基本步骤和书写格式.
能灵活地运用“边角边”基本事实、“角边角” 基本事实、 “边边边” 基本事实和定理“角角边”定理判定两个三角形全等.
对推理证明的要求,应进一步熟练和提高.
【学习重点】
1.重点是了解全等三角形的三条基本事实及“角角边”定理,掌握证明三角形全等的基本步骤和书写格式.
2.能灵活运用课本知识解决全等的相关问题.
【学习过程】
一、复习回顾
自学课本《三角形的有关证明》第1节《全等三角形》的第1课时内容,完成《学案》中的预习作业:
1.能够完全重合的两个图形叫做全等图形;能够______________叫做全等三角形.
2.全等三角形的对应边__________、对应角__________.
3.关于三角形全等的基本事实分别是:
(1) ______________________________的两个三角形全等(SSS)
(2) ______________________________的两个三角形全等(SAS)
(3) ______________________________的两个三角形全等(ASA)
4. (1)三个角对应相等的两个三角形全等吗?
(2)两边和其中一边的对角对应相等的两个三角形全等吗?
(3)两角分别相等且其中一组等角的对边相等的两个三角形全等吗?
5.在证明三角形全等的书写格式上应注意什么?
二、合作探究
探究1
关于“两角分别相等且其中一组等角的对边相等的两个三角形全等”这个结论,你能用有关的基本事实和已经证明过的定理证明它吗?
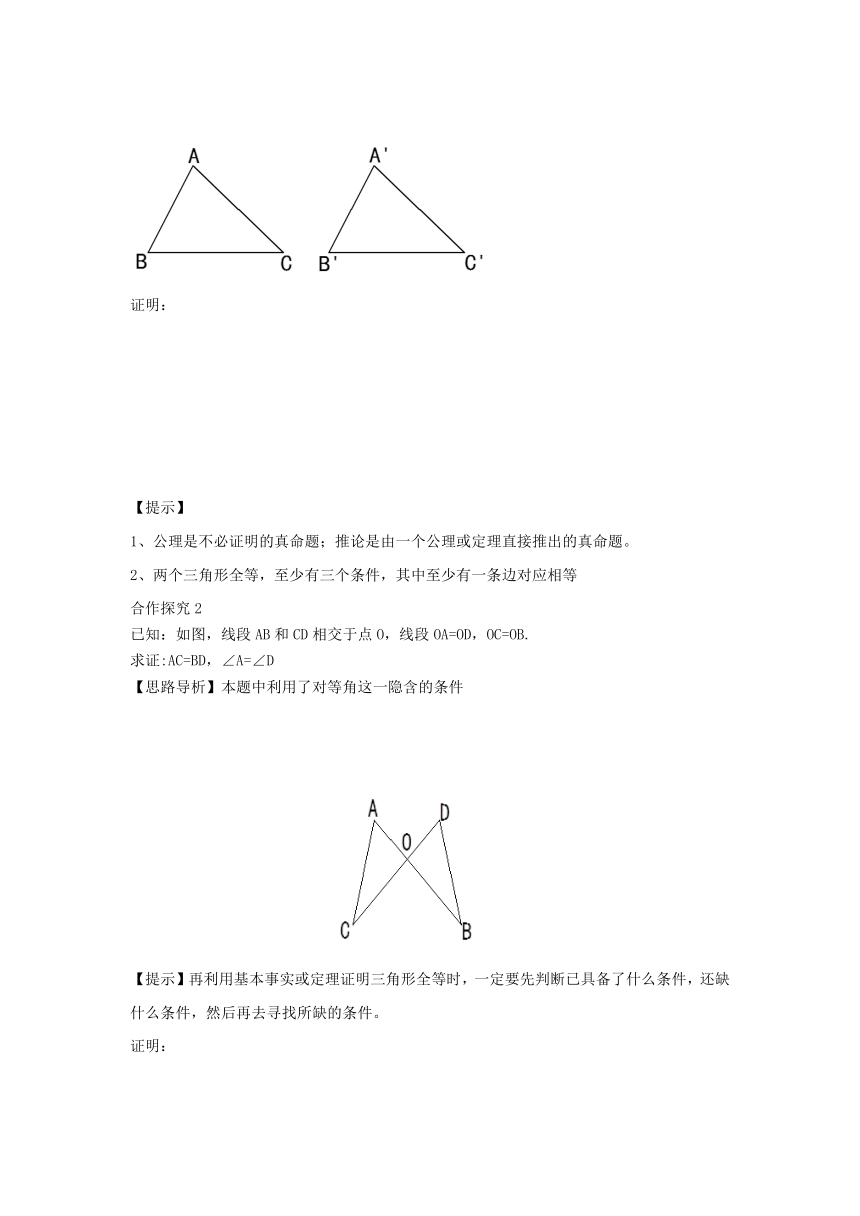
已知:如图,在△ABC和△A'B'C'中,∠B=∠B',∠C=∠C',AB=A'B'?.
求证:△ABC≌△A'B'C'?.
?????????????????????????????????????????????????????????????????????????????????????????????????
证明:
【提示】
1、公理是不必证明的真命题;推论是由一个公理或定理直接推出的真命题。
2、两个三角形全等,至少有三个条件,其中至少有一条边对应相等
合作探究2
已知:如图,线段AB和CD相交于点O,线段OA=OD,OC=OB.
求证:AC=BD,∠A=∠D
【思路导析】本题中利用了对等角这一隐含的条件
???????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? ??????
【提示】再利用基本事实或定理证明三角形全等时,一定要先判断已具备了什么条件,还缺什么条件,然后再去寻找所缺的条件。
证明:
三、巩固提升
1.已知:如图,AB与CD相交于点O,△AOC≌△DOB.
求证:△ABD≌△DCA
?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
证明:∵△AOC≌△DOB
∴AO=DO,CO=BO,AC=BD(????????????????? )
∴_______+________=________+_________ (??????????? )
即AB=DC
在△ABD和△DCA中
∴△ABD≌△DCA (??????? )
????????????????
2. 已知:如图∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?3.已知:如图,点A, D, B, E 在同一条直线上, AC∥DF, BC∥EF,AD=BE.
求证:BC=EF.
?????????????????????????????????????????????????????????????
?四、总结
说说这节课学到的知识点、解决问题的方法.
【学习目标】
了解作为证明基础的几条基本事实的内容,掌握证明的基本步骤和书写格式.
能灵活地运用“边角边”基本事实、“角边角” 基本事实、 “边边边” 基本事实和定理“角角边”定理判定两个三角形全等.
对推理证明的要求,应进一步熟练和提高.
【学习重点】
1.重点是了解全等三角形的三条基本事实及“角角边”定理,掌握证明三角形全等的基本步骤和书写格式.
2.能灵活运用课本知识解决全等的相关问题.
【学习过程】
一、复习回顾
自学课本《三角形的有关证明》第1节《全等三角形》的第1课时内容,完成《学案》中的预习作业:
1.能够完全重合的两个图形叫做全等图形;能够______________叫做全等三角形.
2.全等三角形的对应边__________、对应角__________.
3.关于三角形全等的基本事实分别是:
(1) ______________________________的两个三角形全等(SSS)
(2) ______________________________的两个三角形全等(SAS)
(3) ______________________________的两个三角形全等(ASA)
4. (1)三个角对应相等的两个三角形全等吗?
(2)两边和其中一边的对角对应相等的两个三角形全等吗?
(3)两角分别相等且其中一组等角的对边相等的两个三角形全等吗?
5.在证明三角形全等的书写格式上应注意什么?
二、合作探究
探究1
关于“两角分别相等且其中一组等角的对边相等的两个三角形全等”这个结论,你能用有关的基本事实和已经证明过的定理证明它吗?
已知:如图,在△ABC和△A'B'C'中,∠B=∠B',∠C=∠C',AB=A'B'?.
求证:△ABC≌△A'B'C'?.
?????????????????????????????????????????????????????????????????????????????????????????????????
证明:
【提示】
1、公理是不必证明的真命题;推论是由一个公理或定理直接推出的真命题。
2、两个三角形全等,至少有三个条件,其中至少有一条边对应相等
合作探究2
已知:如图,线段AB和CD相交于点O,线段OA=OD,OC=OB.
求证:AC=BD,∠A=∠D
【思路导析】本题中利用了对等角这一隐含的条件
???????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? ??????
【提示】再利用基本事实或定理证明三角形全等时,一定要先判断已具备了什么条件,还缺什么条件,然后再去寻找所缺的条件。
证明:
三、巩固提升
1.已知:如图,AB与CD相交于点O,△AOC≌△DOB.
求证:△ABD≌△DCA
?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
证明:∵△AOC≌△DOB
∴AO=DO,CO=BO,AC=BD(????????????????? )
∴_______+________=________+_________ (??????????? )
即AB=DC
在△ABD和△DCA中
∴△ABD≌△DCA (??????? )
????????????????
2. 已知:如图∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?3.已知:如图,点A, D, B, E 在同一条直线上, AC∥DF, BC∥EF,AD=BE.
求证:BC=EF.
?????????????????????????????????????????????????????????????
?四、总结
说说这节课学到的知识点、解决问题的方法.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
