基本不等式应用
图片预览








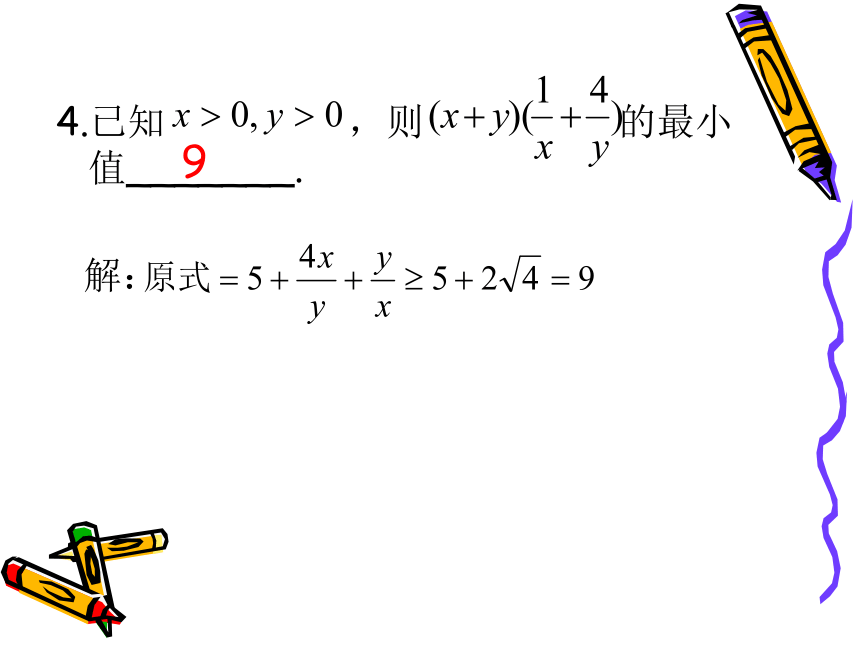
文档简介
(共29张PPT)
基本不等式
【考纲要求】
1.本节内容在高考要求中是C级知识点,即理解、掌握并运用;
2.复习并掌握重要不等式及它的变式的应用;
4.应用均值不等式(极值定理--“和定积最大,积定和最小” )求最大(小)值。
3.理解均值不等式的关系:
【考点诠释】
重点:能灵活利用均值不等式及其变式解决有关证明和求值问题;
难点:要充分注意极值定理的应用条件:
“一正,二定,三相等”。当不具备极值
定理的条件时可采用函数单调性或其他
方法处理。
【教材复习】
(1)基本不等式成立的条件:
1.基本不等式:
a
b
(3)几何意义:
“半弦小于半径”
(2)等号成立的条件:当且仅当 时取等号
2.几个重要的不等式
(1)
(2)
(3)
【基础训练】
1.下列函数中,最小值为4的是________.
①
②
③
④
③
2.若正数a,b满足ab=a+b+3,则ab的取值范围是_______.
[9,+∞)
解:ab=a+b+3
3.如果log3m+log3n≥4,那么m+n的最小值为_______.
18
解:由题意log3mn ≥4从而mn ≥ 81
4.已知 ,则 的最小值_______.
9
解:
例1: 已知 , ,求x+y的最小值。
取等条件不同
误解:由
得
而
【典例解析】 题型一:利用不等式求最值
正解:
当且仅当 时取等号
变式1:
x>0,y>0 且2x-8y-xy=0,求x+y的最小值。
解法一:由题意得2x+8y=xy
例2:已知x>1,求x+ 的最小值以及取得最小值时x的值。
当且仅当x-1= 时取“=”号。
于是x=2或者x=0(舍去)
构造积为定值
解:∵x>1 ∴x-1>0
∴x+ =(x-1)+ +1
变式1:
x>0,y>0 且2x-8y-xy=0,求x+y的最小值。
解法二:由题意得
变式2:
设函数 ,则函数f(x)的最大值为_____
解:
负变正
题型二:利用不等式解应用题
( )
解:(1)
x
x
x
y
)
2
6
4
2
(
5
.
0
100
+
+
+
+
+
+
=
L
5
.
1
100
+
+
=
x
x
y
即
0
>
x
探究拓展:
(1)解应用题时,一定要注意变量的实际意义,也就是其取值范围。
(2)在求函数最值时,除应用基本不等式外,有时会出现基本不等式取不到“=”,此时应考虑函数的单调性。
(2)由均值不等式得
5
.
21
5
.
1
100
2
5
.
1
100
=
+
×
+
+
=
x
x
x
x
y
当且仅当 ,即x=10时取等号
x
x
100
=
题型三:不等式的证明
例4:已知 求证:
思维点拨:由于不等式左边含字母a,b右边无字母,直接使用基本不等式既无法约掉字母,不等号方向又不对,因a+b=1,能否把左边展开,实行“1”的代换。
证:
当且仅当 时取等号
变式3:
已知 ,求证:
证:
当且仅当时 取等号
【反思感悟】
1. 成立的条件是 ,而
成立,则要求a≥0且b≥0。使用时,要明确定理成立的前提条件。
2.在运用均值不等式时,存在前提“一正二定三相等,”三个条件缺一不可。
3.注意掌握均值不等式的逆运用。
【走近高考】
1.(08年江苏卷)设x,y,z为正实数,满足 ,则 的最小值是______
解:由 得
代入 得
当且仅当x=3z时取等号
2.(06年上海卷)若a,b,c>0且a(a+b+c)+bc= ,则2a+b+c的最小值为______
解:
4.(08年重庆卷)若a是1+2b与1-2b的等比中项,则 的最大值为____
解:a是1+2b与1-2b的等比中项,
则
【课堂小结】
公式的正用、逆用和变形用;
公式条件:正、定、等;
构造“和定”或“积定”求最值。
应用题:弄清题意,建立模型
基本不等式
【考纲要求】
1.本节内容在高考要求中是C级知识点,即理解、掌握并运用;
2.复习并掌握重要不等式及它的变式的应用;
4.应用均值不等式(极值定理--“和定积最大,积定和最小” )求最大(小)值。
3.理解均值不等式的关系:
【考点诠释】
重点:能灵活利用均值不等式及其变式解决有关证明和求值问题;
难点:要充分注意极值定理的应用条件:
“一正,二定,三相等”。当不具备极值
定理的条件时可采用函数单调性或其他
方法处理。
【教材复习】
(1)基本不等式成立的条件:
1.基本不等式:
a
b
(3)几何意义:
“半弦小于半径”
(2)等号成立的条件:当且仅当 时取等号
2.几个重要的不等式
(1)
(2)
(3)
【基础训练】
1.下列函数中,最小值为4的是________.
①
②
③
④
③
2.若正数a,b满足ab=a+b+3,则ab的取值范围是_______.
[9,+∞)
解:ab=a+b+3
3.如果log3m+log3n≥4,那么m+n的最小值为_______.
18
解:由题意log3mn ≥4从而mn ≥ 81
4.已知 ,则 的最小值_______.
9
解:
例1: 已知 , ,求x+y的最小值。
取等条件不同
误解:由
得
而
【典例解析】 题型一:利用不等式求最值
正解:
当且仅当 时取等号
变式1:
x>0,y>0 且2x-8y-xy=0,求x+y的最小值。
解法一:由题意得2x+8y=xy
例2:已知x>1,求x+ 的最小值以及取得最小值时x的值。
当且仅当x-1= 时取“=”号。
于是x=2或者x=0(舍去)
构造积为定值
解:∵x>1 ∴x-1>0
∴x+ =(x-1)+ +1
变式1:
x>0,y>0 且2x-8y-xy=0,求x+y的最小值。
解法二:由题意得
变式2:
设函数 ,则函数f(x)的最大值为_____
解:
负变正
题型二:利用不等式解应用题
( )
解:(1)
x
x
x
y
)
2
6
4
2
(
5
.
0
100
+
+
+
+
+
+
=
L
5
.
1
100
+
+
=
x
x
y
即
0
>
x
探究拓展:
(1)解应用题时,一定要注意变量的实际意义,也就是其取值范围。
(2)在求函数最值时,除应用基本不等式外,有时会出现基本不等式取不到“=”,此时应考虑函数的单调性。
(2)由均值不等式得
5
.
21
5
.
1
100
2
5
.
1
100
=
+
×
+
+
=
x
x
x
x
y
当且仅当 ,即x=10时取等号
x
x
100
=
题型三:不等式的证明
例4:已知 求证:
思维点拨:由于不等式左边含字母a,b右边无字母,直接使用基本不等式既无法约掉字母,不等号方向又不对,因a+b=1,能否把左边展开,实行“1”的代换。
证:
当且仅当 时取等号
变式3:
已知 ,求证:
证:
当且仅当时 取等号
【反思感悟】
1. 成立的条件是 ,而
成立,则要求a≥0且b≥0。使用时,要明确定理成立的前提条件。
2.在运用均值不等式时,存在前提“一正二定三相等,”三个条件缺一不可。
3.注意掌握均值不等式的逆运用。
【走近高考】
1.(08年江苏卷)设x,y,z为正实数,满足 ,则 的最小值是______
解:由 得
代入 得
当且仅当x=3z时取等号
2.(06年上海卷)若a,b,c>0且a(a+b+c)+bc= ,则2a+b+c的最小值为______
解:
4.(08年重庆卷)若a是1+2b与1-2b的等比中项,则 的最大值为____
解:a是1+2b与1-2b的等比中项,
则
【课堂小结】
公式的正用、逆用和变形用;
公式条件:正、定、等;
构造“和定”或“积定”求最值。
应用题:弄清题意,建立模型
