第二十九章 投影与视图单元质量检测试卷C(含答案)
文档属性
| 名称 | 第二十九章 投影与视图单元质量检测试卷C(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 19:56:28 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版2020-2021学年九年级(下)第二十九章投影与视图检测试卷C
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
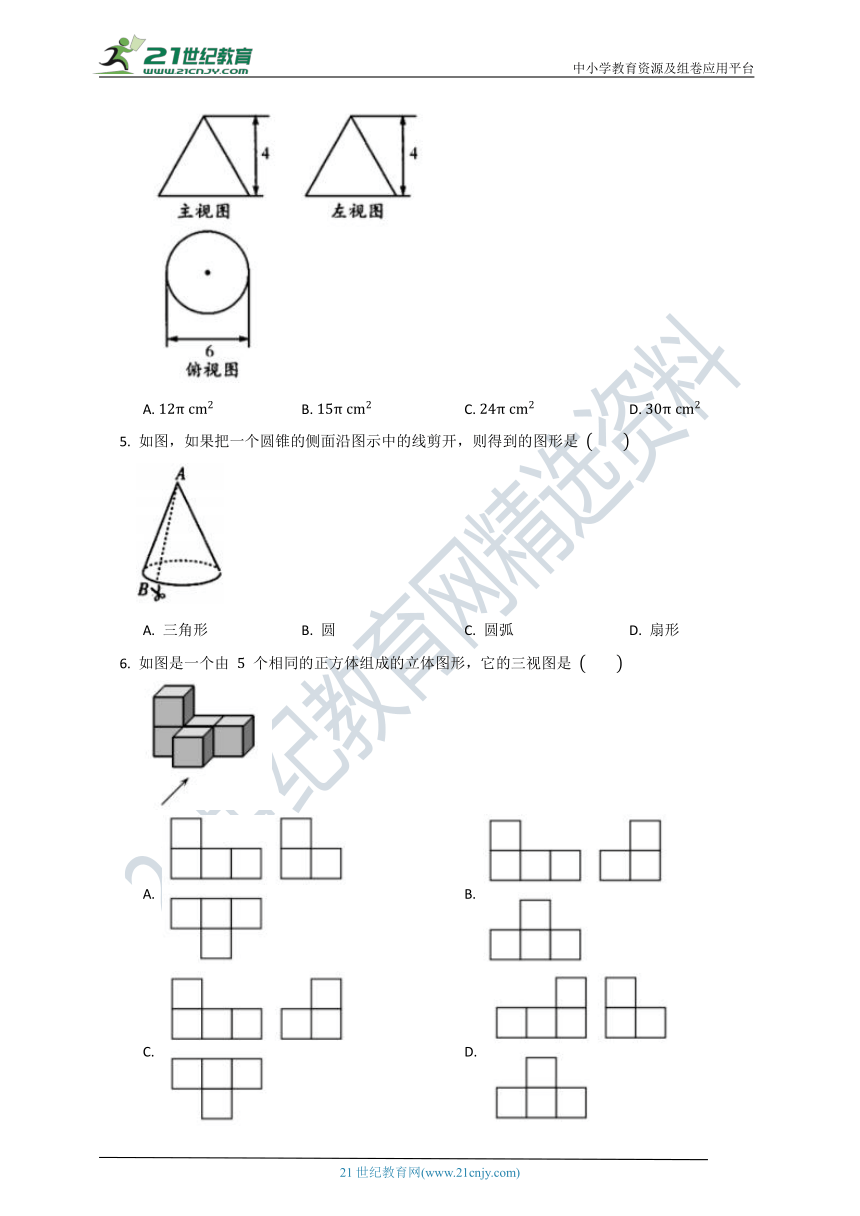
1.
用
个完全相同的小正方体组合成如图所示的立体图形,它的俯视图为
A.
B.
C.
D.
2.
如图,箭头表示投影线的方向,则图中圆柱体的正投影是
A.
圆
B.
圆柱
C.
梯形
D.
矩形
3.
在一个晴朗的好天气里,小颖在向正北方向走路时,发现自己的身影向左偏,你知道小颖当时所处的时间是
A.
上午
B.
下午
C.
黄昏
D.
无法确定
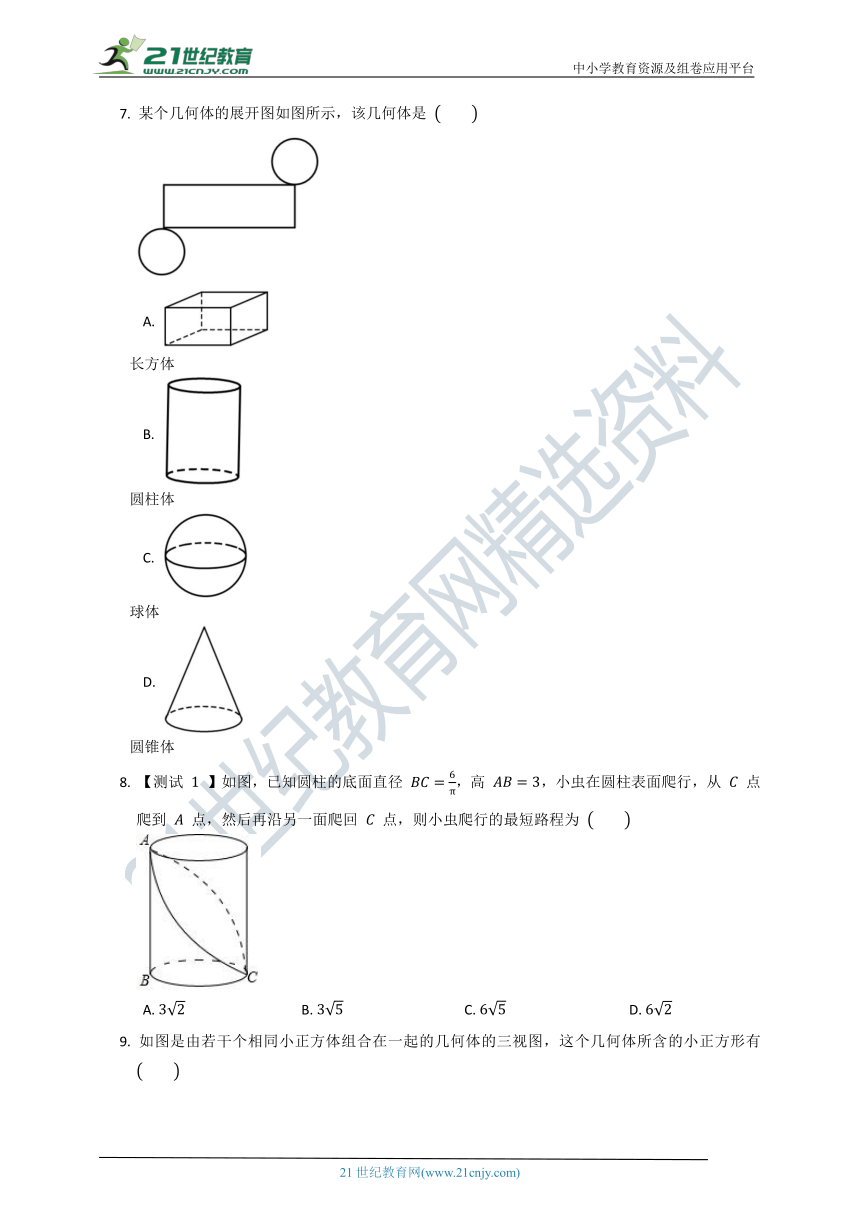
4.
已知一个圆锥体的三视图如图所示,则这个圆锥的侧面积为
A.
B.
C.
D.
5.
如图,如果把一个圆锥的侧面沿图示中的线剪开,则得到的图形是
A.
三角形
B.
圆
C.
圆弧
D.
扇形
6.
如图是一个由
个相同的正方体组成的立体图形,它的三视图是
A.
B.
C.
D.
7.
某个几何体的展开图如图所示,该几何体是
A.
长方体
B.
圆柱体
C.
球体
D.
圆锥体
8.
【测试
】如图,已知圆柱的底面直径
,高
,小虫在圆柱表面爬行,从
点爬到
点,然后再沿另一面爬回
点,则小虫爬行的最短路程为
A.
B.
C.
D.
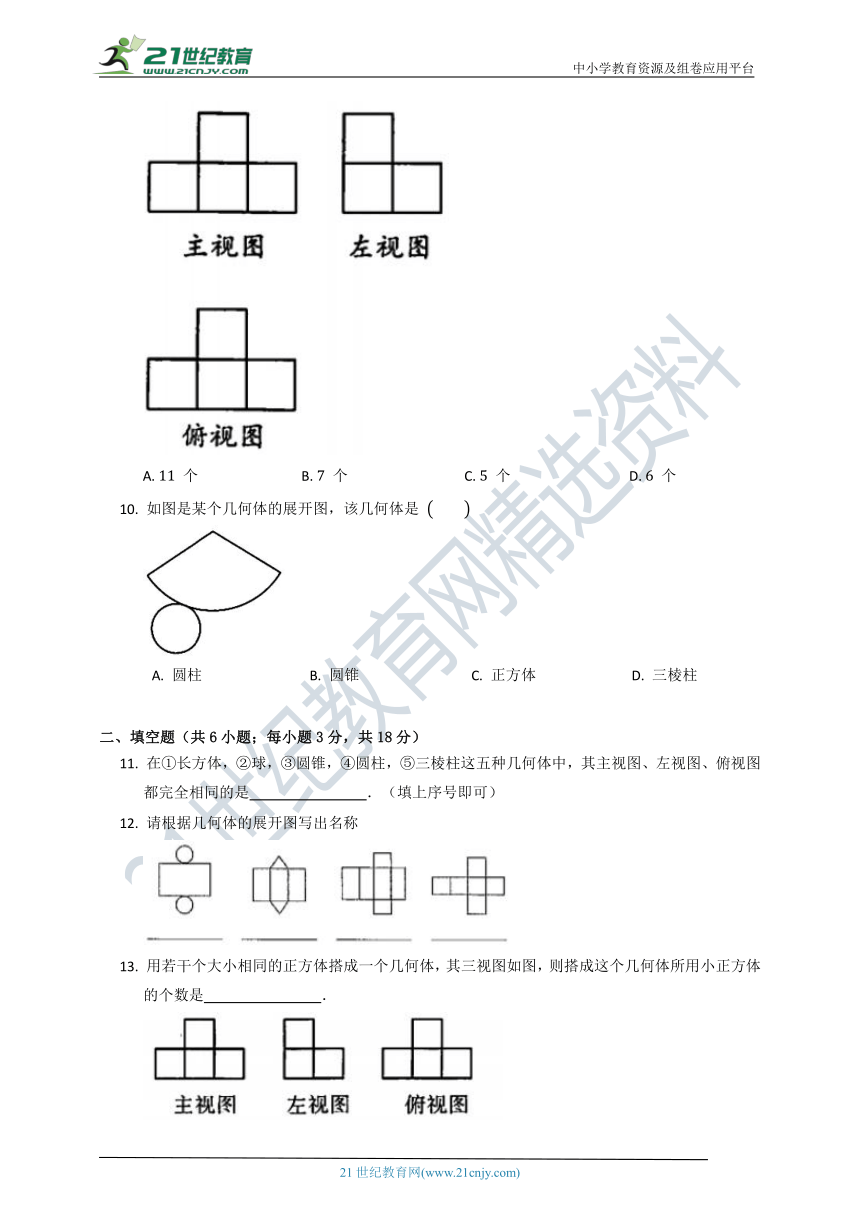
9.
如图是由若干个相同小正方体组合在一起的几何体的三视图,这个几何体所含的小正方形有
A.
个
B.
个
C.
个
D.
个
10.
如图是某个几何体的展开图,该几何体是
A.
圆柱
B.
圆锥
C.
正方体
D.
三棱柱
二、填空题(共6小题;每小题3分,共18分)
11.
在①长方体,②球,③圆锥,④圆柱,⑤三棱柱这五种几何体中,其主视图、左视图、俯视图都完全相同的是
?.(填上序号即可)
12.
请根据几何体的展开图写出名称
13.
用若干个大小相同的正方体搭成一个几何体,其三视图如图,则搭成这个几何体所用小正方体的个数是
?.
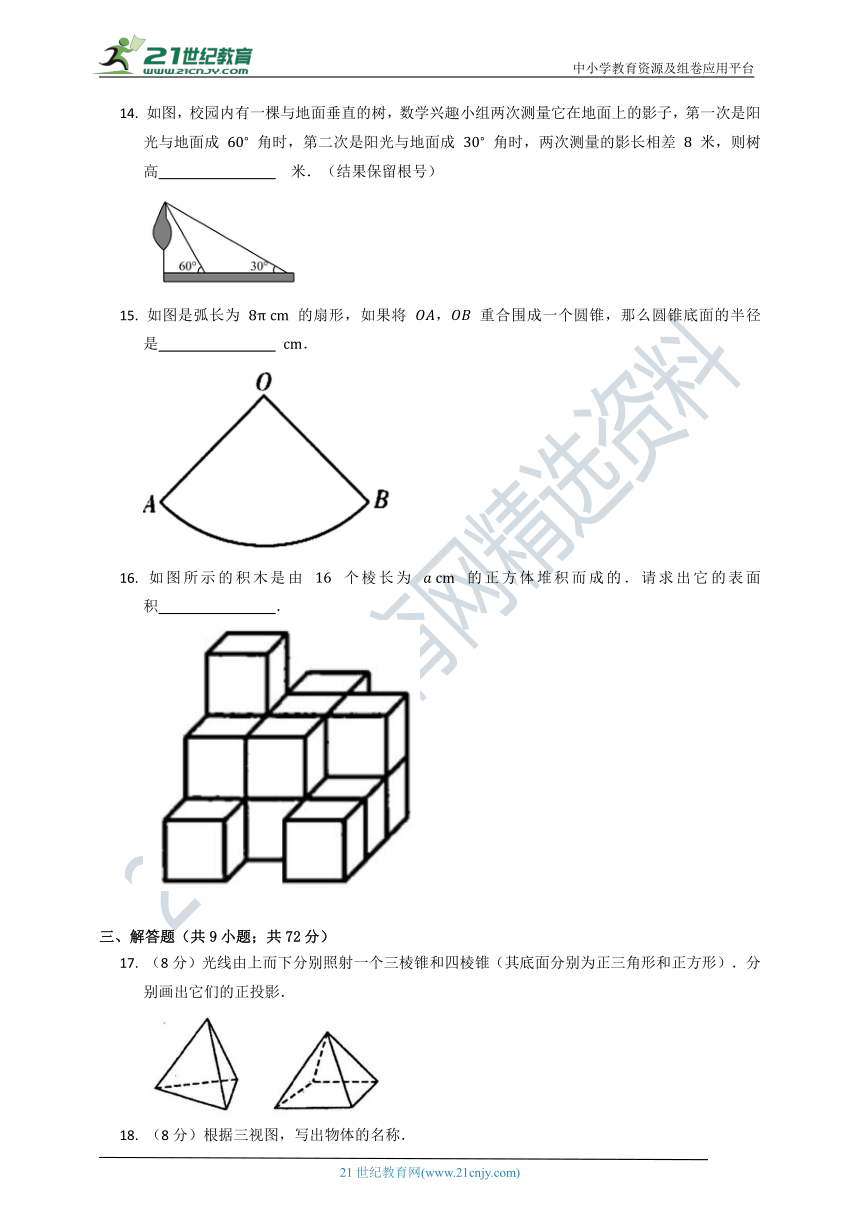
14.
如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成
角时,第二次是阳光与地面成
角时,两次测量的影长相差
米,则树高
?
米.(结果保留根号)
15.
如图是弧长为
的扇形,如果将
,
重合围成一个圆锥,那么圆锥底面的半径是
?
.
16.
如图所示的积木是由
个棱长为
的正方体堆积而成的.请求出它的表面积
?.
三、解答题(共9小题;共72分)
17.
(8分)光线由上而下分别照射一个三棱锥和四棱锥(其底面分别为正三角形和正方形).分别画出它们的正投影.
18.
(8分)根据三视图,写出物体的名称.
(1)
(2)
19.
(8分)一个几何体的三视图如下图所示,如果一只蚂蚁要从这个几何体中的点
出发,沿表面爬到
的中点
,请你求出这个线路的最短路程.
20.
(8分)把一根直的细铁丝(记为线段
)放在三个不同的位置:
()铁丝平行于投影面;
()铁丝倾斜于投影面;
()铁丝垂直于投影面.
三种情况下铁丝的正投影各是什么形状?
21.
(8分)
个棱长为
的正方体组成如图的几何体.
(1)该几何体的体积是
?(立方单位),表面积是
?(平方单位).
(2)画出该几何体的主视图和左视图.
22.
(8分)一个直三棱柱的立体图如图所示,它的底面是等边三角形,请画出它的三视图.
23.
(8分)
如图是一个几何体的平面展开图.
(1)这个几何体是
?.
(2)求这个几何体的体积.(
取
)
24.
(8分)如图,从一个直径是
的圆形铁皮中剪下一个圆心角为
的扇形.
(1)求这个扇形的面积(结果保留
);
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由;
(3)当
的半径
为任意值时,(2)中的结论是否仍然成立?请说明理由.
25.
(8分)转化”是一种重要的数学思想,将空间问题转化为平面问题是转化思想的一个重要方面,例如,如图①,一个立方体的棱长为
,有一只蚂蚁从
点出发,沿着立方体的表面爬行到点
,沿怎样的路线爬行路程最短?要解决这个问题,我们可以把立方体展开(如图②③),把空间两个面上的两点
、
之间的最短路径问题转化为同一个面上两点之间的距离问题.根据“两点之间线段最短”,可知蚂蚁沿线段
爬行路径最短,最短路径长为
.
下面请你思考蚂蚁在圆锥表面的爬行问题:如图④,圆锥的底面半径为
,母线长为
.一只蚂蚁从圆锥底面圆周上一点
出发,沿着圆锥的侧面爬过一圈到达母线
的中点
.问:蚂蚁爬行的最短路径长是多少?
答案
第一部分
1.
C
2.
D
3.
A
4.
B
5.
D
6.
A
7.
B
8.
D
【解析】把圆柱侧面展开,如图所示,
点
,
间最短距离为线段
的长.
在
中,,,
为底面圆周长的一半,即
,
所以
,
即最短路程为
,
故选:D.
9.
C
10.
B
第二部分
11.
②
12.
圆柱,三棱柱,长方体,正方体
13.
个
14.
15.
16.
第三部分
17.
18.
(1)
长方体.
??????(2)
圆锥.
19.
如图
,
,
,
最短路程为
.
20.
()线段,且
.
()线段,且
.
()点
21.
(1)
;
??????(2)
22.
23.
(1)
圆柱
??????(2)
体积:.
24.
(1)
如图①,连接
,
在
中,,
是
的直径,
.
又在
中,,
是等腰直角三角形,
由勾股定理得
,
扇形的面积为
.
??????(2)
不能,理由如下:
如图②,延长
,交
于点
,交
于点
,则
.
以
为直径作
,则
的半径为
,
的周长为
.
的长为
,
的周长
的长,
不能围成一个圆锥.
??????(3)
仍然成立,理由如下:
的半径为
,则
.
的长为
.
,
的半径为
.
的周长为
.
,,
,
的周长
的长,
不能围成一个圆锥.
即(2)中结论仍然成立.
25.
蚂蚁爬行的最短路径是在圆锥侧面展开图扇形中线段
的距离,如图..
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
人教版2020-2021学年九年级(下)第二十九章投影与视图检测试卷C
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1.
用
个完全相同的小正方体组合成如图所示的立体图形,它的俯视图为
A.
B.
C.
D.
2.
如图,箭头表示投影线的方向,则图中圆柱体的正投影是
A.
圆
B.
圆柱
C.
梯形
D.
矩形
3.
在一个晴朗的好天气里,小颖在向正北方向走路时,发现自己的身影向左偏,你知道小颖当时所处的时间是
A.
上午
B.
下午
C.
黄昏
D.
无法确定
4.
已知一个圆锥体的三视图如图所示,则这个圆锥的侧面积为
A.
B.
C.
D.
5.
如图,如果把一个圆锥的侧面沿图示中的线剪开,则得到的图形是
A.
三角形
B.
圆
C.
圆弧
D.
扇形
6.
如图是一个由
个相同的正方体组成的立体图形,它的三视图是
A.
B.
C.
D.
7.
某个几何体的展开图如图所示,该几何体是
A.
长方体
B.
圆柱体
C.
球体
D.
圆锥体
8.
【测试
】如图,已知圆柱的底面直径
,高
,小虫在圆柱表面爬行,从
点爬到
点,然后再沿另一面爬回
点,则小虫爬行的最短路程为
A.
B.
C.
D.
9.
如图是由若干个相同小正方体组合在一起的几何体的三视图,这个几何体所含的小正方形有
A.
个
B.
个
C.
个
D.
个
10.
如图是某个几何体的展开图,该几何体是
A.
圆柱
B.
圆锥
C.
正方体
D.
三棱柱
二、填空题(共6小题;每小题3分,共18分)
11.
在①长方体,②球,③圆锥,④圆柱,⑤三棱柱这五种几何体中,其主视图、左视图、俯视图都完全相同的是
?.(填上序号即可)
12.
请根据几何体的展开图写出名称
13.
用若干个大小相同的正方体搭成一个几何体,其三视图如图,则搭成这个几何体所用小正方体的个数是
?.
14.
如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成
角时,第二次是阳光与地面成
角时,两次测量的影长相差
米,则树高
?
米.(结果保留根号)
15.
如图是弧长为
的扇形,如果将
,
重合围成一个圆锥,那么圆锥底面的半径是
?
.
16.
如图所示的积木是由
个棱长为
的正方体堆积而成的.请求出它的表面积
?.
三、解答题(共9小题;共72分)
17.
(8分)光线由上而下分别照射一个三棱锥和四棱锥(其底面分别为正三角形和正方形).分别画出它们的正投影.
18.
(8分)根据三视图,写出物体的名称.
(1)
(2)
19.
(8分)一个几何体的三视图如下图所示,如果一只蚂蚁要从这个几何体中的点
出发,沿表面爬到
的中点
,请你求出这个线路的最短路程.
20.
(8分)把一根直的细铁丝(记为线段
)放在三个不同的位置:
()铁丝平行于投影面;
()铁丝倾斜于投影面;
()铁丝垂直于投影面.
三种情况下铁丝的正投影各是什么形状?
21.
(8分)
个棱长为
的正方体组成如图的几何体.
(1)该几何体的体积是
?(立方单位),表面积是
?(平方单位).
(2)画出该几何体的主视图和左视图.
22.
(8分)一个直三棱柱的立体图如图所示,它的底面是等边三角形,请画出它的三视图.
23.
(8分)
如图是一个几何体的平面展开图.
(1)这个几何体是
?.
(2)求这个几何体的体积.(
取
)
24.
(8分)如图,从一个直径是
的圆形铁皮中剪下一个圆心角为
的扇形.
(1)求这个扇形的面积(结果保留
);
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由;
(3)当
的半径
为任意值时,(2)中的结论是否仍然成立?请说明理由.
25.
(8分)转化”是一种重要的数学思想,将空间问题转化为平面问题是转化思想的一个重要方面,例如,如图①,一个立方体的棱长为
,有一只蚂蚁从
点出发,沿着立方体的表面爬行到点
,沿怎样的路线爬行路程最短?要解决这个问题,我们可以把立方体展开(如图②③),把空间两个面上的两点
、
之间的最短路径问题转化为同一个面上两点之间的距离问题.根据“两点之间线段最短”,可知蚂蚁沿线段
爬行路径最短,最短路径长为
.
下面请你思考蚂蚁在圆锥表面的爬行问题:如图④,圆锥的底面半径为
,母线长为
.一只蚂蚁从圆锥底面圆周上一点
出发,沿着圆锥的侧面爬过一圈到达母线
的中点
.问:蚂蚁爬行的最短路径长是多少?
答案
第一部分
1.
C
2.
D
3.
A
4.
B
5.
D
6.
A
7.
B
8.
D
【解析】把圆柱侧面展开,如图所示,
点
,
间最短距离为线段
的长.
在
中,,,
为底面圆周长的一半,即
,
所以
,
即最短路程为
,
故选:D.
9.
C
10.
B
第二部分
11.
②
12.
圆柱,三棱柱,长方体,正方体
13.
个
14.
15.
16.
第三部分
17.
18.
(1)
长方体.
??????(2)
圆锥.
19.
如图
,
,
,
最短路程为
.
20.
()线段,且
.
()线段,且
.
()点
21.
(1)
;
??????(2)
22.
23.
(1)
圆柱
??????(2)
体积:.
24.
(1)
如图①,连接
,
在
中,,
是
的直径,
.
又在
中,,
是等腰直角三角形,
由勾股定理得
,
扇形的面积为
.
??????(2)
不能,理由如下:
如图②,延长
,交
于点
,交
于点
,则
.
以
为直径作
,则
的半径为
,
的周长为
.
的长为
,
的周长
的长,
不能围成一个圆锥.
??????(3)
仍然成立,理由如下:
的半径为
,则
.
的长为
.
,
的半径为
.
的周长为
.
,,
,
的周长
的长,
不能围成一个圆锥.
即(2)中结论仍然成立.
25.
蚂蚁爬行的最短路径是在圆锥侧面展开图扇形中线段
的距离,如图..
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
