新教材2021-2022学年高中数学人教A版(2019)必修第一册课件:5.5.1 第2课时 两角和与差的正弦、余弦、正切公式(45张PPT)
文档属性
| 名称 | 新教材2021-2022学年高中数学人教A版(2019)必修第一册课件:5.5.1 第2课时 两角和与差的正弦、余弦、正切公式(45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-20 14:31:07 | ||
图片预览








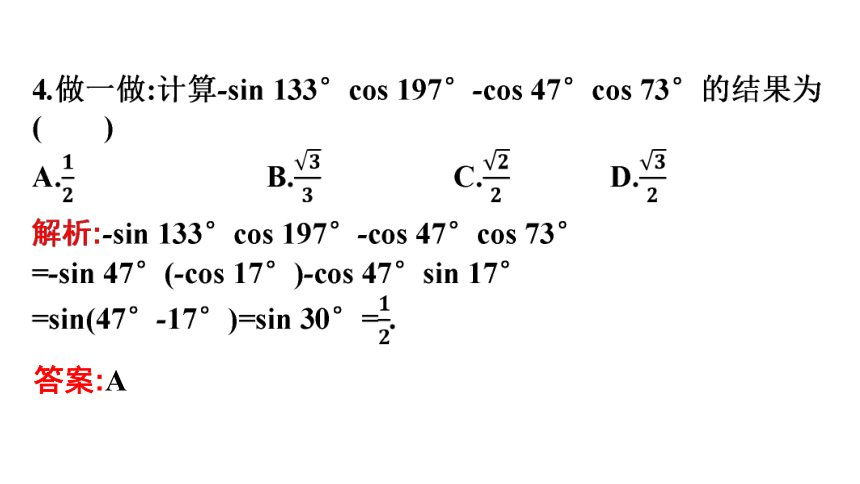



文档简介
5.5.1 两角和与差的正弦、余弦、正切公式
第2课时 两角和与差的正弦、余弦、正切公式
课标定位
素养阐释
1.能从两角差的余弦公式推导出两角和与差的正弦、余弦、正切公式.
2.熟记两角和与差的正弦、余弦、正切公式的形式及符号特征,并能利用该公式进行求值、计算.
3.体会类比推理的过程,加强逻辑推理能力和数学运算能力的培养.
自主预习·新知导学
合作探究·释疑解惑
易 错 辨 析
随 堂 练 习
自主预习·新知导学
一、两角和的余弦公式
【问题思考】
1.如何由两角差的余弦公式得到两角和的余弦公式?
提示:用-β代换公式cos(α-β)=cos αcos β+sin αsin β中的β便可得到.
2.填空:cos(α+β)= cos αcos β-sin αsin β .(C(α+β))?
答案:A
二、两角和与差的正弦公式
【问题思考】
1.如何利用两角差的余弦公式和诱导公式得到两角和的正弦公式?
2.怎样由两角和的正弦公式得到两角差的正弦公式?
提示:用-β代换β,可得sin(α-β)=sin αcos β-cos αsin β.
3.填空:两角和与差的正弦公式
记忆口诀:“正余余正,符号相同”.
答案:A
三、两角和与差的正切公式
【问题思考】
1.怎样由两角和的正弦、余弦公式得到两角和的正切公式?
2.由两角和的正切公式如何得到两角差的正切公式?
提示:用-β替换公式tan(α+β)中的β即可得到.
3.填空:(1)两角和与差的正切公式
(2)S(α+β),C(α+β),T(α+β)都叫做和角公式;S(α-β),C(α-β),T(α-β)都叫做差角公式.
答案:1
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
合作探究·释疑解惑
探究一 给角求值
反思感悟
1.对于非特殊角的三角函数式,要想利用两角和与差的正弦、余弦、正切公式求出具体数值,一般有以下三种途径
(1)化为特殊角的三角函数值;
(2)化为正负相消的项,相消去求值;
(3)化为分子、分母形式,先约分再求值.
2.在进行求值过程的变换中,一定要本着先整体后局部的基本原则.整体分析三角函数式的特点,如果整体符合三角公式,那么整体变形,否则要进行局部的变换.
探究二 给值求值(角)
1.例2的条件不变,如何求cos(α-β)的值?
反思感悟
1.给值(式)求值问题的解题策略
(1)当“已知角”有两个时,“所求角”一般表示为两个“已知角”的和或差的形式;
(2)当“已知角”有一个时,此时应先着眼于“所求角”与“已知角”的和或差的关系,再应用诱导公式把“所求角”变成“已知角”.
2.给值求角问题本质上为给值求值问题,解题时应注意对角的取值范围加以讨论,以免产生增解或漏解.
答案:B
探究三 和角、差角公式的变形使用
分析:(1)因为23°+37°=60°,所以可逆用正切公式求解;(2)先提取公因数,再利用辅助角公式求解.
反思感悟
1.两角和与差的正切公式有两种变形形式
2.研究形如f(x)=asin x+bcos x的函数的性质都要用到辅助角公式进行变换.
易 错 辨 析
忽略角的取值范围致错
以上解答过程中都有哪些错误?出错的原因是什么?你如何改正?你如何防范?
提示:没有依据题设条件进一步缩小角α,β的取值范围,导致2α-β的取值范围过大而致误.
防范措施
随 堂 练 习
答案:D
答案:A
答案:B
答案:7
第2课时 两角和与差的正弦、余弦、正切公式
课标定位
素养阐释
1.能从两角差的余弦公式推导出两角和与差的正弦、余弦、正切公式.
2.熟记两角和与差的正弦、余弦、正切公式的形式及符号特征,并能利用该公式进行求值、计算.
3.体会类比推理的过程,加强逻辑推理能力和数学运算能力的培养.
自主预习·新知导学
合作探究·释疑解惑
易 错 辨 析
随 堂 练 习
自主预习·新知导学
一、两角和的余弦公式
【问题思考】
1.如何由两角差的余弦公式得到两角和的余弦公式?
提示:用-β代换公式cos(α-β)=cos αcos β+sin αsin β中的β便可得到.
2.填空:cos(α+β)= cos αcos β-sin αsin β .(C(α+β))?
答案:A
二、两角和与差的正弦公式
【问题思考】
1.如何利用两角差的余弦公式和诱导公式得到两角和的正弦公式?
2.怎样由两角和的正弦公式得到两角差的正弦公式?
提示:用-β代换β,可得sin(α-β)=sin αcos β-cos αsin β.
3.填空:两角和与差的正弦公式
记忆口诀:“正余余正,符号相同”.
答案:A
三、两角和与差的正切公式
【问题思考】
1.怎样由两角和的正弦、余弦公式得到两角和的正切公式?
2.由两角和的正切公式如何得到两角差的正切公式?
提示:用-β替换公式tan(α+β)中的β即可得到.
3.填空:(1)两角和与差的正切公式
(2)S(α+β),C(α+β),T(α+β)都叫做和角公式;S(α-β),C(α-β),T(α-β)都叫做差角公式.
答案:1
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
合作探究·释疑解惑
探究一 给角求值
反思感悟
1.对于非特殊角的三角函数式,要想利用两角和与差的正弦、余弦、正切公式求出具体数值,一般有以下三种途径
(1)化为特殊角的三角函数值;
(2)化为正负相消的项,相消去求值;
(3)化为分子、分母形式,先约分再求值.
2.在进行求值过程的变换中,一定要本着先整体后局部的基本原则.整体分析三角函数式的特点,如果整体符合三角公式,那么整体变形,否则要进行局部的变换.
探究二 给值求值(角)
1.例2的条件不变,如何求cos(α-β)的值?
反思感悟
1.给值(式)求值问题的解题策略
(1)当“已知角”有两个时,“所求角”一般表示为两个“已知角”的和或差的形式;
(2)当“已知角”有一个时,此时应先着眼于“所求角”与“已知角”的和或差的关系,再应用诱导公式把“所求角”变成“已知角”.
2.给值求角问题本质上为给值求值问题,解题时应注意对角的取值范围加以讨论,以免产生增解或漏解.
答案:B
探究三 和角、差角公式的变形使用
分析:(1)因为23°+37°=60°,所以可逆用正切公式求解;(2)先提取公因数,再利用辅助角公式求解.
反思感悟
1.两角和与差的正切公式有两种变形形式
2.研究形如f(x)=asin x+bcos x的函数的性质都要用到辅助角公式进行变换.
易 错 辨 析
忽略角的取值范围致错
以上解答过程中都有哪些错误?出错的原因是什么?你如何改正?你如何防范?
提示:没有依据题设条件进一步缩小角α,β的取值范围,导致2α-β的取值范围过大而致误.
防范措施
随 堂 练 习
答案:D
答案:A
答案:B
答案:7
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
