新教材2021-2022学年高中数学人教A版(2019)必修第一册课件:5.5.1 第3课时 二倍角的正弦、余弦、正切公式(38张PPT)
文档属性
| 名称 | 新教材2021-2022学年高中数学人教A版(2019)必修第一册课件:5.5.1 第3课时 二倍角的正弦、余弦、正切公式(38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 935.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-20 14:32:28 | ||
图片预览







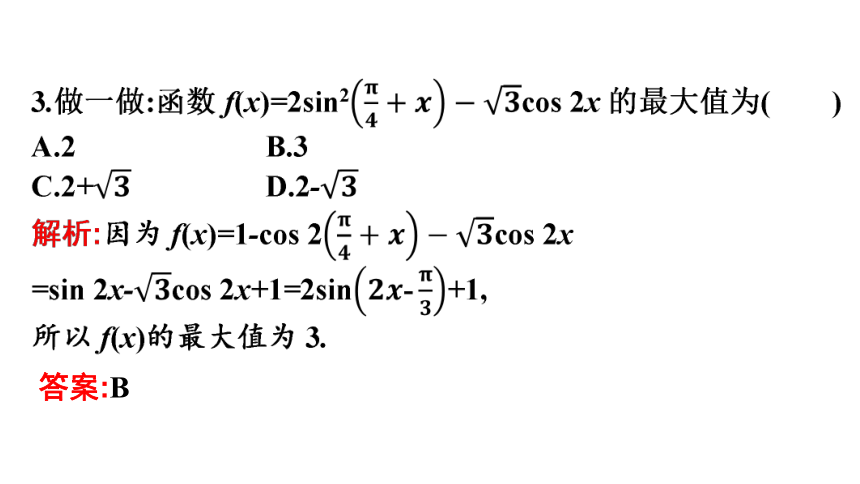



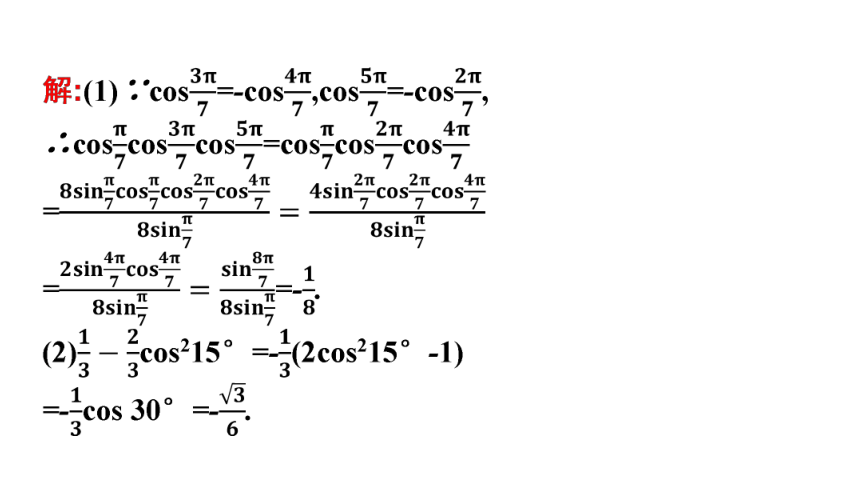
文档简介
5.5.1 两角和与差的正弦、余弦、正切公式
第3课时 二倍角的正弦、余弦、正切公式
课标定位
素养阐释
1.能从两角和的正弦、余弦、正切公式推导出二倍角的正弦、余弦、正切公式.
2.能熟练运用二倍角的公式进行简单的恒等变换,并能灵活地将公式变形运用.
3.体会类比推理的过程,加强逻辑推理能力和数学运算能力的培养.
自主预习·新知导学
合作探究·释疑解惑
易 错 辨 析
随 堂 练 习
自主预习·新知导学
一、二倍角公式的推导
【问题思考】
1.你能用S(α±β),C(α±β),T(α±β)推导出sin 2α,cos 2α,tan 2α的公式吗?
2.填空:二倍角的正弦、余弦、正切公式
二、二倍角的余弦公式的变形
【问题思考】
1.根据同角三角函数的基本关系sin2α+cos2α=1,能否只用sin α或cos α表示cos 2α?
提示:cos 2α=cos2α-sin2α=cos2α-(1-cos2α)=2cos2α-1;
或cos 2α=cos2α-sin2α=(1-sin2α)-sin2α=1-2sin2α.
2.填空:cos 2α= 1-2sin2α ,cos 2α= 2cos2α-1 .
答案:B
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)二倍角的正弦、余弦、正切公式的适用范围是任意角.
( × )
(2)存在角α,使得sin 2α=2sin α成立.( √ )
(3)对任意角α,cos 2α=2cos α都不成立.( × )
合作探究·释疑解惑
探究一 给角求值
反思感悟
对于给角求值问题,一般有两类
(1)直接正用、逆用二倍角公式,结合诱导公式和同角三角函数的基本关系对已知式子进行转化,一般可以化为特殊角.
(2)若形式为几个非特殊角的三角函数式相乘,则一般逆用二倍角的正弦公式.在求解过程中,需利用互余关系配凑出应用二倍角公式的条件,使得问题出现可以连用二倍角的正弦公式的形式.
探究二 给值求值(角)
1.若例2的条件不变,求sin 4α的值.
反思感悟
三角函数的条件求值问题常有两种解题途径
(1)对题设条件变形,把条件中的角、函数名向结论中的角、函数名靠拢;
(2)对结论变形,将结论中的角、函数名向题设条件中的角、函数名靠拢,以便将题设条件代入结论.
答案:A
探究三 利用倍角公式化简、证明
分析:首先切化弦,然后利用二倍角公式统一角,最后化简得结果.
反思感悟
1.化简的方法
(1)弦切互化,异名化同名,异角化同角;
(2)降幂或升幂.
2.证明恒等式,要观察恒等式两端的结构形式,处理原则是从复杂到简单,高次到低次,复角化单角;如果两端都比较复杂,那么将两端都化简,即采用“两头凑”的思想.
易 错 辨 析
以上解答过程中都有哪些错误?出错的原因是什么?你如何改正?你如何防范?
防范措施
盲目地运用公式化简函数的解析式,而忽略函数的定义域,是解决与三角函数有关问题的易错点.要想正确求解,需要掌握倍角、分角的终边所在象限的确定方法.
答案:0
随 堂 练 习
答案:B
答案:B
答案:A
答案:6
第3课时 二倍角的正弦、余弦、正切公式
课标定位
素养阐释
1.能从两角和的正弦、余弦、正切公式推导出二倍角的正弦、余弦、正切公式.
2.能熟练运用二倍角的公式进行简单的恒等变换,并能灵活地将公式变形运用.
3.体会类比推理的过程,加强逻辑推理能力和数学运算能力的培养.
自主预习·新知导学
合作探究·释疑解惑
易 错 辨 析
随 堂 练 习
自主预习·新知导学
一、二倍角公式的推导
【问题思考】
1.你能用S(α±β),C(α±β),T(α±β)推导出sin 2α,cos 2α,tan 2α的公式吗?
2.填空:二倍角的正弦、余弦、正切公式
二、二倍角的余弦公式的变形
【问题思考】
1.根据同角三角函数的基本关系sin2α+cos2α=1,能否只用sin α或cos α表示cos 2α?
提示:cos 2α=cos2α-sin2α=cos2α-(1-cos2α)=2cos2α-1;
或cos 2α=cos2α-sin2α=(1-sin2α)-sin2α=1-2sin2α.
2.填空:cos 2α= 1-2sin2α ,cos 2α= 2cos2α-1 .
答案:B
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)二倍角的正弦、余弦、正切公式的适用范围是任意角.
( × )
(2)存在角α,使得sin 2α=2sin α成立.( √ )
(3)对任意角α,cos 2α=2cos α都不成立.( × )
合作探究·释疑解惑
探究一 给角求值
反思感悟
对于给角求值问题,一般有两类
(1)直接正用、逆用二倍角公式,结合诱导公式和同角三角函数的基本关系对已知式子进行转化,一般可以化为特殊角.
(2)若形式为几个非特殊角的三角函数式相乘,则一般逆用二倍角的正弦公式.在求解过程中,需利用互余关系配凑出应用二倍角公式的条件,使得问题出现可以连用二倍角的正弦公式的形式.
探究二 给值求值(角)
1.若例2的条件不变,求sin 4α的值.
反思感悟
三角函数的条件求值问题常有两种解题途径
(1)对题设条件变形,把条件中的角、函数名向结论中的角、函数名靠拢;
(2)对结论变形,将结论中的角、函数名向题设条件中的角、函数名靠拢,以便将题设条件代入结论.
答案:A
探究三 利用倍角公式化简、证明
分析:首先切化弦,然后利用二倍角公式统一角,最后化简得结果.
反思感悟
1.化简的方法
(1)弦切互化,异名化同名,异角化同角;
(2)降幂或升幂.
2.证明恒等式,要观察恒等式两端的结构形式,处理原则是从复杂到简单,高次到低次,复角化单角;如果两端都比较复杂,那么将两端都化简,即采用“两头凑”的思想.
易 错 辨 析
以上解答过程中都有哪些错误?出错的原因是什么?你如何改正?你如何防范?
防范措施
盲目地运用公式化简函数的解析式,而忽略函数的定义域,是解决与三角函数有关问题的易错点.要想正确求解,需要掌握倍角、分角的终边所在象限的确定方法.
答案:0
随 堂 练 习
答案:B
答案:B
答案:A
答案:6
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
