陕西省黄陵中学2020-2021学年高一下学期期中考试数学(文)试题 Word版含答案
文档属性
| 名称 | 陕西省黄陵中学2020-2021学年高一下学期期中考试数学(文)试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 292.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-19 18:45:29 | ||
图片预览

文档简介
黄陵中学2020-2021学年度第二学期期中考试
高一数学(文)试题
【参考公式或数据】
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
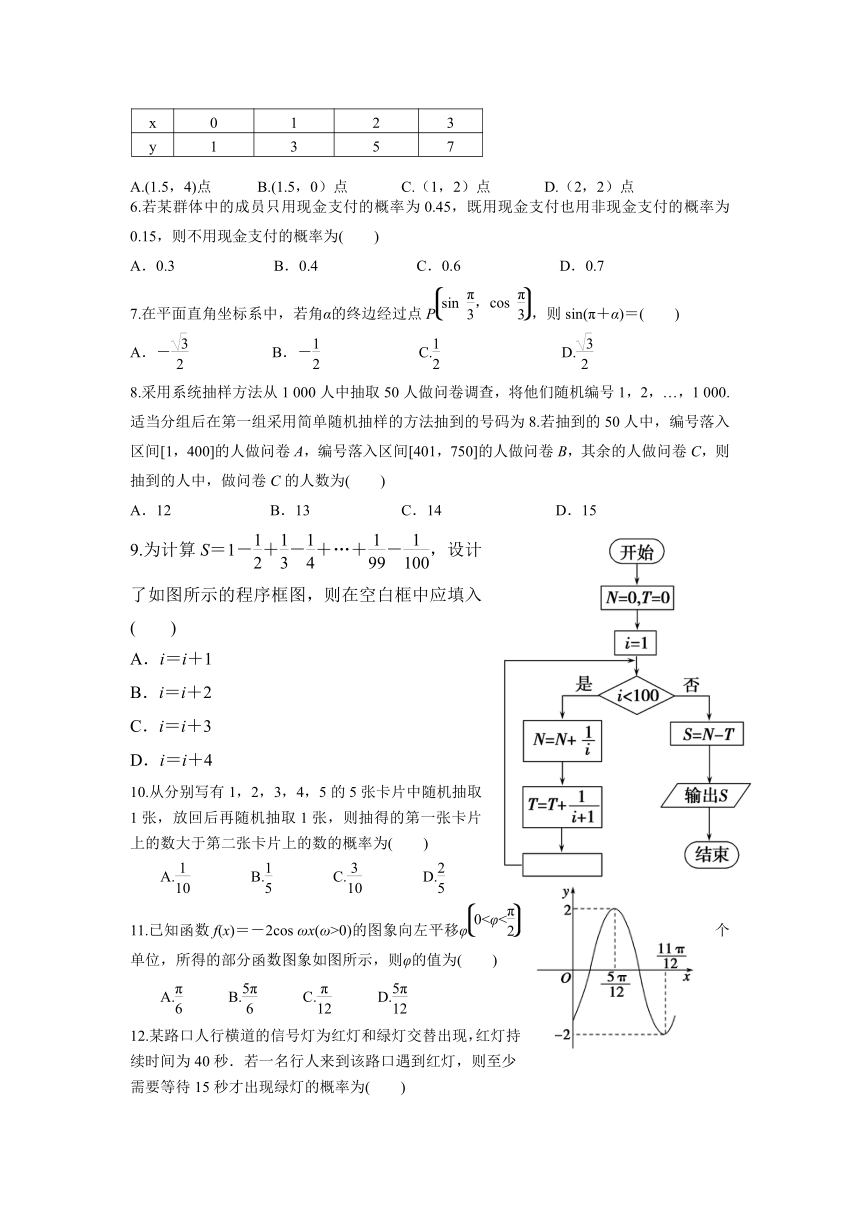
1. 对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);对变量u,v,有观测数据(ui,vi)(i=1,2,…,10),得散点图(2),由这两个散点图可以判断( )
A.变量x与y正相关,u与v正相关 B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关 D.变量x与y负相关,u与v负相关
2.甲,乙两组数的数据如茎叶图所示,则甲,乙的平均数,方差,极差及中位数相同的是( )
A.极差 B.方差 C.平均数 D.中位数
3.根据右边程序框图,当输入10时,输出的是( )
A.12 B.19 C.14.1 D.-30
4.函数的最小正周期为( )
A.4π B.2π C.π D.
5. 已知x与y之间的一组数据:则y与x的线性回归方程为y=bx+a必过( )
x 0 1 2 3
y 1 3 5 7
A.(1.5,4)点 B.(1.5,0)点 C.(1,2)点 D.(2,2)点
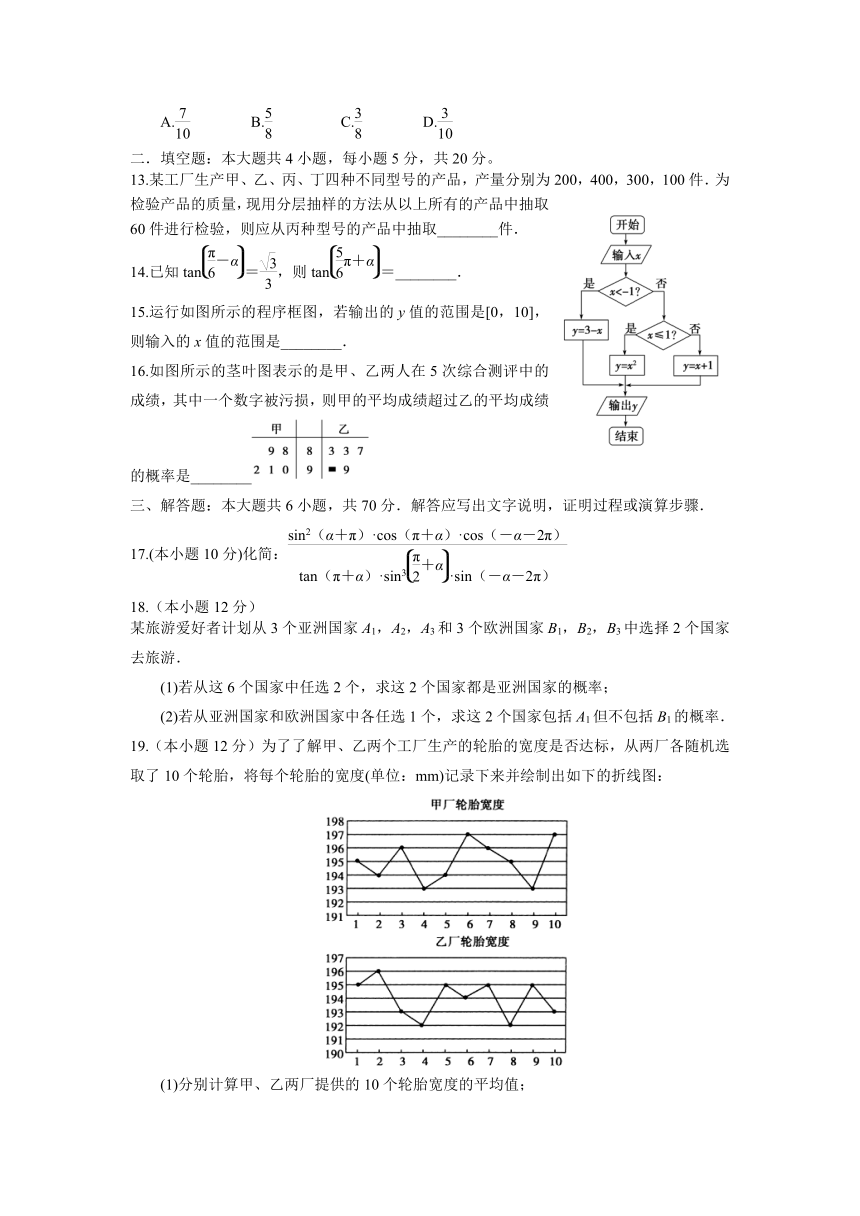
6.若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为( )
A.0.3 B.0.4 C.0.6 D.0.7
7.在平面直角坐标系中,若角α的终边经过点P,则sin(π+α)=( )
A.- B.- C. D.
8.采用系统抽样方法从1 000人中抽取50人做问卷调查,将他们随机编号1,2,…,1 000.适当分组后在第一组采用简单随机抽样的方法抽到的号码为8.若抽到的50人中,编号落入区间[1,400]的人做问卷A,编号落入区间[401,750]的人做问卷B,其余的人做问卷C,则抽到的人中,做问卷C的人数为( )
A.12 B.13 C.14 D.15
9.为计算S=1-+-+…+-,设计了如图所示的程序框图,则在空白框中应填入( )
A.i=i+1
B.i=i+2
C.i=i+3
D.i=i+4
10.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )
A. B. C. D.
11.已知函数f(x)=-2cos ωx(ω>0)的图象向左平移φ个单位,所得的部分函数图象如图所示,则φ的值为( )
A. B. C. D.
12.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持
续时间为40秒.若一名行人来到该路口遇到红灯,则至少
需要等待15秒才出现绿灯的概率为( )
A. B. C. D.
二.填空题:本大题共4小题,每小题5分,共20分。
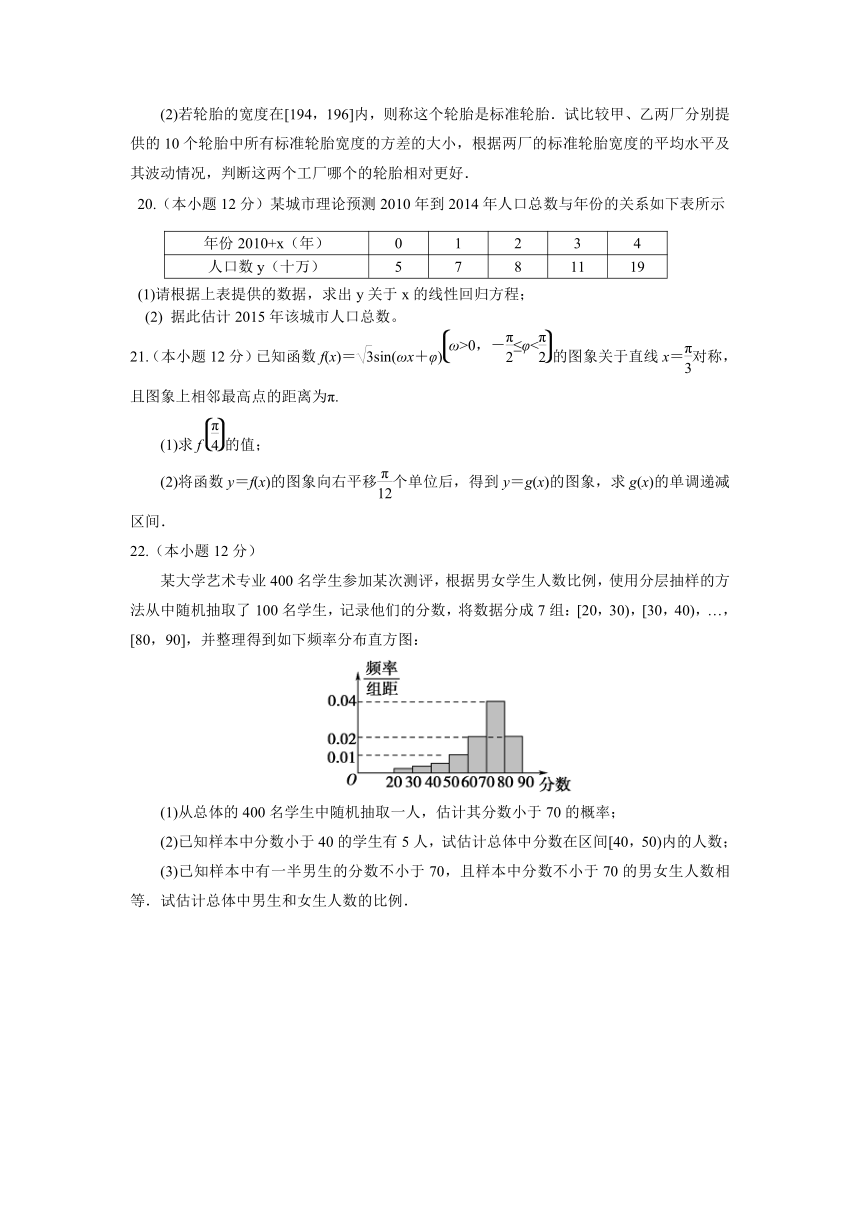
13.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件.为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取________件.
14.已知tan=,则tan=________.
15.运行如图所示的程序框图,若输出的y值的范围是[0,10],则输入的x值的范围是________.
16.如图所示的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率是________
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题10分)化简:
18.(本小题12分)
某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率.
19.(本小题12分)为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,从两厂各随机选取了10个轮胎,将每个轮胎的宽度(单位:mm)记录下来并绘制出如下的折线图:
(1)分别计算甲、乙两厂提供的10个轮胎宽度的平均值;
(2)若轮胎的宽度在[194,196]内,则称这个轮胎是标准轮胎.试比较甲、乙两厂分别提供的10个轮胎中所有标准轮胎宽度的方差的大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个的轮胎相对更好.
20.(本小题12分)某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) 0 1 2 3 4
人口数y(十万) 5 7 8 11 19
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。
21.(本小题12分)已知函数f(x)=sin(ωx+φ)的图象关于直线x=对称,且图象上相邻最高点的距离为π.
(1)求f的值;
(2)将函数y=f(x)的图象向右平移个单位后,得到y=g(x)的图象,求g(x)的单调递减区间.
22.(本小题12分)
某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(1)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
1 2 3 4 5 6 7 8 9 10 11 12
C C C C A B B A B D C B
17.(本小题10分)化简:
解析:原式===1.
18.(本小题12分)
解:(1)由题意知,从6个国家中任选两个国家,其一切可能的结果组成的基本事件有{A1,A2},{A1,A3},{A1,B1},{A1,B2},{A1,B3},{A2,A3},{A2,B1},{A2,B2},{A2,B3},{A3,B1},{A3,B2},{A3,B3},{B1,B2},{B1,B3},{B2,B3},共15个.
所选两个国家都是亚洲国家的事件所包含的基本事件有{A1,A2},{A1,A3},{A2,A3},共3个,则所求事件的概率为P==.
(2)从亚洲国家和欧洲国家中各任选一个,其一切可能的结果组成的基本事件有{A1,B1},{A1,B2},{A1,B3},{A2,B1},{A2,B2},{A2,B3},{A3,B1},{A3,B2},{A3,B3},共9个.
包括A1但不包括B1的事件所包含的基本事件有{A1,B2},{A1,B3},共2个,则所求事件的概率为P=.
19.(本小题12分)
解:(1)甲厂10个轮胎宽度的平均值:甲=×(195+194+196+193+194+197+196+195+193+197)=195(mm),
乙厂10个轮胎宽度的平均值:乙=×(195+196+193+192+195+194+195+192+195+193)=194(mm).
(2)甲厂10个轮胎中宽度在[194,196]内的数据为195,194,196,194,196,195,
平均数:1=×(195+194+196+194+196+195)=195,
方差:s=×[(195-195)2+(194-195)2+(196-195)2+(194-195)2+(196-195)2+(195-195)2]=,
乙厂10个轮胎中宽度在[194,196]内的数据为195,196,195,194,195,195,
平均数:2=×(195+196+195+194+195+195)=195,
方差:s=×[(195-195)2+(196-195)2+(195-195)2+(194-195)2+(195-195)2+(195-195)2]=,
因为两厂标准轮胎宽度的平均数相等,但乙厂的方差更小,
所以乙厂的轮胎相对更好.
20.(本小题12分)
解:(1),
= 0×5+1×7+2×8+3×11+4×19=132,
=
故y关于x的线性回归方程为=3.2x+3.6
(2)当x=5时,=3.2×5+3.6即=19.6
据此估计2015年该城市人口总数约为196万.
21.(本小题12分)
解:(1)因为f(x)的图象上相邻最高点的距离为π,
所以f(x)的最小正周期T=π,从而ω==2.
又f(x)的图象关于直线x=对称,
所以2×+φ=kπ+(k∈Z),
因为-≤φ<,
所以φ=-,所以f(x)=sin=sin.
则f=sin=sin =.
(2)将f(x)的图象向右平移个单位后,得到f的图象,
所以g(x)=f=sin
所以φ=-+kπ,(k∈Z).
当2kπ+≤2x-≤2kπ+(k∈Z),
即kπ+≤x≤kπ+(k∈Z)时,g(x)单调递减.
所以g(x)的单调递减区间为(k∈Z).
22.(本小题12分)
解:(1)根据频率分布直方图可知,样本中分数不小于70的频率为(0.02+0.所以样本中分数小于70的频率为1-0.6=0.4,
所以从总体的400名学生中随机抽取一人,其分数小于70的概率估计为0.4.
(2)根据题意,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,
分数在区间[40,50)内的人数为100-100×0.9-5=5,
所以总体中分数在区间[40,50)内的人数估计为400×=20.
(3)由题意可知,样本中分数不小于70的学生人数为(0.02+0.04)×10×100=60,
所以样本中分数不小于70的男生人数为60×=30,
所以样本中的男生人数为30×2=60,
女生人数为100-60=40,
男生和女生人数的比例为60∶40=3∶2,
所以根据分层抽样原理,总体中男生和女生人数的比例估计为3∶2.
高一数学(文)试题
【参考公式或数据】
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);对变量u,v,有观测数据(ui,vi)(i=1,2,…,10),得散点图(2),由这两个散点图可以判断( )
A.变量x与y正相关,u与v正相关 B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关 D.变量x与y负相关,u与v负相关
2.甲,乙两组数的数据如茎叶图所示,则甲,乙的平均数,方差,极差及中位数相同的是( )
A.极差 B.方差 C.平均数 D.中位数
3.根据右边程序框图,当输入10时,输出的是( )
A.12 B.19 C.14.1 D.-30
4.函数的最小正周期为( )
A.4π B.2π C.π D.
5. 已知x与y之间的一组数据:则y与x的线性回归方程为y=bx+a必过( )
x 0 1 2 3
y 1 3 5 7
A.(1.5,4)点 B.(1.5,0)点 C.(1,2)点 D.(2,2)点
6.若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为( )
A.0.3 B.0.4 C.0.6 D.0.7
7.在平面直角坐标系中,若角α的终边经过点P,则sin(π+α)=( )
A.- B.- C. D.
8.采用系统抽样方法从1 000人中抽取50人做问卷调查,将他们随机编号1,2,…,1 000.适当分组后在第一组采用简单随机抽样的方法抽到的号码为8.若抽到的50人中,编号落入区间[1,400]的人做问卷A,编号落入区间[401,750]的人做问卷B,其余的人做问卷C,则抽到的人中,做问卷C的人数为( )
A.12 B.13 C.14 D.15
9.为计算S=1-+-+…+-,设计了如图所示的程序框图,则在空白框中应填入( )
A.i=i+1
B.i=i+2
C.i=i+3
D.i=i+4
10.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )
A. B. C. D.
11.已知函数f(x)=-2cos ωx(ω>0)的图象向左平移φ个单位,所得的部分函数图象如图所示,则φ的值为( )
A. B. C. D.
12.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持
续时间为40秒.若一名行人来到该路口遇到红灯,则至少
需要等待15秒才出现绿灯的概率为( )
A. B. C. D.
二.填空题:本大题共4小题,每小题5分,共20分。
13.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件.为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取________件.
14.已知tan=,则tan=________.
15.运行如图所示的程序框图,若输出的y值的范围是[0,10],则输入的x值的范围是________.
16.如图所示的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率是________
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题10分)化简:
18.(本小题12分)
某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率.
19.(本小题12分)为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,从两厂各随机选取了10个轮胎,将每个轮胎的宽度(单位:mm)记录下来并绘制出如下的折线图:
(1)分别计算甲、乙两厂提供的10个轮胎宽度的平均值;
(2)若轮胎的宽度在[194,196]内,则称这个轮胎是标准轮胎.试比较甲、乙两厂分别提供的10个轮胎中所有标准轮胎宽度的方差的大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个的轮胎相对更好.
20.(本小题12分)某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) 0 1 2 3 4
人口数y(十万) 5 7 8 11 19
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。
21.(本小题12分)已知函数f(x)=sin(ωx+φ)的图象关于直线x=对称,且图象上相邻最高点的距离为π.
(1)求f的值;
(2)将函数y=f(x)的图象向右平移个单位后,得到y=g(x)的图象,求g(x)的单调递减区间.
22.(本小题12分)
某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(1)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
1 2 3 4 5 6 7 8 9 10 11 12
C C C C A B B A B D C B
17.(本小题10分)化简:
解析:原式===1.
18.(本小题12分)
解:(1)由题意知,从6个国家中任选两个国家,其一切可能的结果组成的基本事件有{A1,A2},{A1,A3},{A1,B1},{A1,B2},{A1,B3},{A2,A3},{A2,B1},{A2,B2},{A2,B3},{A3,B1},{A3,B2},{A3,B3},{B1,B2},{B1,B3},{B2,B3},共15个.
所选两个国家都是亚洲国家的事件所包含的基本事件有{A1,A2},{A1,A3},{A2,A3},共3个,则所求事件的概率为P==.
(2)从亚洲国家和欧洲国家中各任选一个,其一切可能的结果组成的基本事件有{A1,B1},{A1,B2},{A1,B3},{A2,B1},{A2,B2},{A2,B3},{A3,B1},{A3,B2},{A3,B3},共9个.
包括A1但不包括B1的事件所包含的基本事件有{A1,B2},{A1,B3},共2个,则所求事件的概率为P=.
19.(本小题12分)
解:(1)甲厂10个轮胎宽度的平均值:甲=×(195+194+196+193+194+197+196+195+193+197)=195(mm),
乙厂10个轮胎宽度的平均值:乙=×(195+196+193+192+195+194+195+192+195+193)=194(mm).
(2)甲厂10个轮胎中宽度在[194,196]内的数据为195,194,196,194,196,195,
平均数:1=×(195+194+196+194+196+195)=195,
方差:s=×[(195-195)2+(194-195)2+(196-195)2+(194-195)2+(196-195)2+(195-195)2]=,
乙厂10个轮胎中宽度在[194,196]内的数据为195,196,195,194,195,195,
平均数:2=×(195+196+195+194+195+195)=195,
方差:s=×[(195-195)2+(196-195)2+(195-195)2+(194-195)2+(195-195)2+(195-195)2]=,
因为两厂标准轮胎宽度的平均数相等,但乙厂的方差更小,
所以乙厂的轮胎相对更好.
20.(本小题12分)
解:(1),
= 0×5+1×7+2×8+3×11+4×19=132,
=
故y关于x的线性回归方程为=3.2x+3.6
(2)当x=5时,=3.2×5+3.6即=19.6
据此估计2015年该城市人口总数约为196万.
21.(本小题12分)
解:(1)因为f(x)的图象上相邻最高点的距离为π,
所以f(x)的最小正周期T=π,从而ω==2.
又f(x)的图象关于直线x=对称,
所以2×+φ=kπ+(k∈Z),
因为-≤φ<,
所以φ=-,所以f(x)=sin=sin.
则f=sin=sin =.
(2)将f(x)的图象向右平移个单位后,得到f的图象,
所以g(x)=f=sin
所以φ=-+kπ,(k∈Z).
当2kπ+≤2x-≤2kπ+(k∈Z),
即kπ+≤x≤kπ+(k∈Z)时,g(x)单调递减.
所以g(x)的单调递减区间为(k∈Z).
22.(本小题12分)
解:(1)根据频率分布直方图可知,样本中分数不小于70的频率为(0.02+0.所以样本中分数小于70的频率为1-0.6=0.4,
所以从总体的400名学生中随机抽取一人,其分数小于70的概率估计为0.4.
(2)根据题意,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,
分数在区间[40,50)内的人数为100-100×0.9-5=5,
所以总体中分数在区间[40,50)内的人数估计为400×=20.
(3)由题意可知,样本中分数不小于70的学生人数为(0.02+0.04)×10×100=60,
所以样本中分数不小于70的男生人数为60×=30,
所以样本中的男生人数为30×2=60,
女生人数为100-60=40,
男生和女生人数的比例为60∶40=3∶2,
所以根据分层抽样原理,总体中男生和女生人数的比例估计为3∶2.
同课章节目录
