人教版八年级下勾股定理课件
文档属性
| 名称 | 人教版八年级下勾股定理课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 770.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-23 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
18.1 勾股定理
第二十四届国际数学家大会
为什么选这个图形作会徽呢?
会 徽
18.1 勾股定理
股
勾
弦
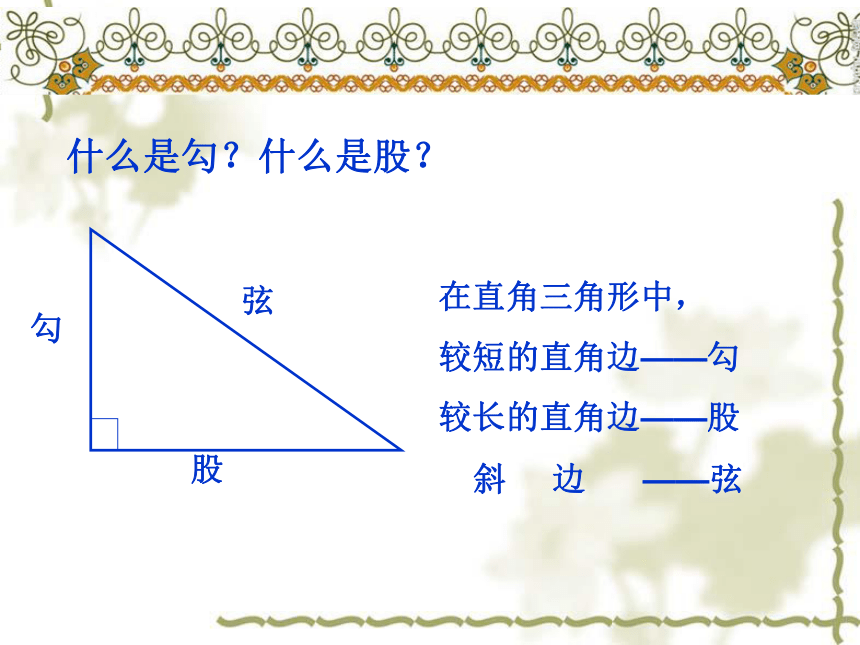
什么是勾?什么是股?
在直角三角形中,
较短的直角边——勾
较长的直角边——股
斜 边 ——弦
勾股定理的对象是——直角三角形的三条边。
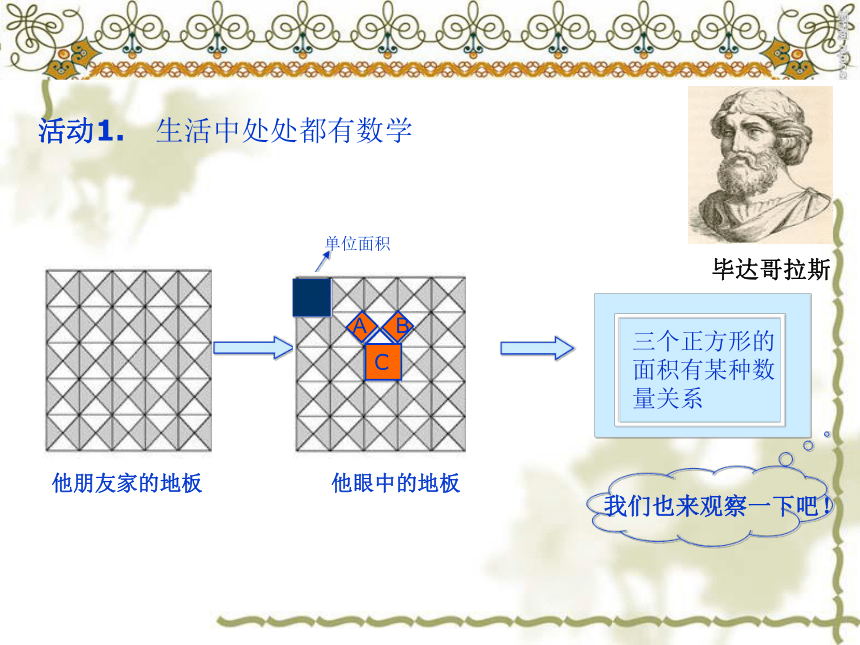
活动1. 生活中处处都有数学
活动2. 这条规律也适用于 一般的直角三角形吗?
活动3: 你能证明命题是正确的吗?
活动4: 原来就是你
毕达哥拉斯
勾股定理 = 毕达哥拉斯定理
我们也来观察一下吧!
毕达哥拉斯
他朋友家的地板
他眼中的地板
三个正方形的面积有某种数量关系
活动1. 生活中处处都有数学
单位面积
A
C
A
B
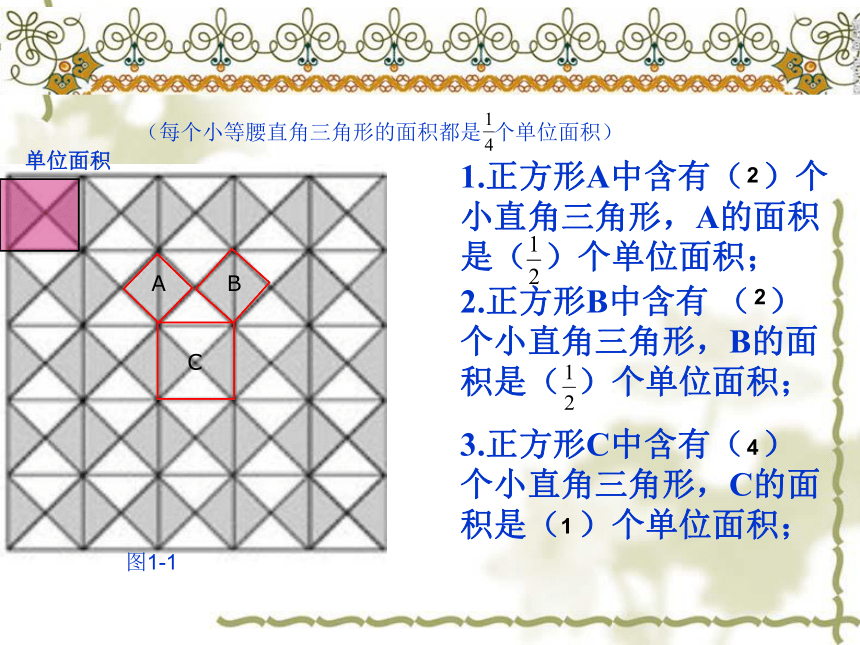
1.正方形A中含有( )个小直角三角形,A的面积是( )个单位面积;
2.正方形B中含有 ( )个小直角三角形,B的面积是( )个单位面积;
3.正方形C中含有( )个小直角三角形,C的面积是( )个单位面积;
单位面积
2
2
4
1
(每个小等腰直角三角形的面积都是 个单位面积)
C
A
B
图1-1
图1-2
1.A的面积是 ( ) 个单位面积;
2.B的面积是( )个单位面积;
3.C的面积是( )个单位面积。
A
B
C
再观察一下图形2:
a
b
c
2
2
4
(每个小等腰直角三角形的面积都是 个单位面积)
正方形A的面积
正方形B的面积
正方形C的面积
图1-1
图1-2
A、B、C的面积关系
等腰直角三角形三边关系
1
2
2
4
A的面积 + B的面积 = C的面积
两直角边的平方和等于斜边的平方
利用图1和图2收集的数据,补充下表:
因此可知等腰直角三角形有这样的性质:
两直角边的平方和等于斜边的平方
A
B
C
图1-3
A
B
C
图1-4
活动2. 这条规律也适用于 一般的直角三角形吗?(每个方格都是单位面积)
A的面积 B的面积 C的面积
图3
图4
A、B、C面积关系
直角三角形三边关系
16
9
4
9
?
?
如何求正方形C的面积呢?
面积分割法:
正方形C的面积
= 4个三角形的面积 +
小正方形的面积
A
B
C
图1-3
A
B
C
图1-4
命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。
c
a
b
由活动1和活动2,我们得到:
你能利用这个图来证明吗?
这个图是1700多年前我国古人赵爽证明这个规律时给出的,所以被称为“赵爽弦图”。
活动3:你能证明命题1是正确的吗?
思想相同
分割面积法
A
B
C
图1-3
A
B
C
图1-4
a
b
c
b
c
a
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
a
b
c
赵爽弦图
b-a
证明:
活动四:原来就是你
命题1被证明是正确的!
正确的命题称为定理。
命题 1
勾股定理
勾股定理:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。
实战演练
例1.在三角形ABC中,角C为直角,
(1)已知b=6,c=10,求a.
(2)已知a=15, b=20,求c.
A
C
B
例1.在三角形ABC中,角C为直角,
(1)已知b=6,c=10,求a.
(2)已知a=15, b=20,求c.
实战演练
解:(1)由勾股定理可得:
(2)由勾股定理可得:
C
A
B
例2.要登上8米高的建筑物BC,为了安全,需使梯子底端离
建筑物的距离AB为6米,问至少需要多长的梯子?
例2.要登上8米高的建筑物BC,为了安全,需使梯子底端离
建筑物的距离AB为6米,问至少需要多长的梯子?
解:由题可知,
为直角三角形,
且
由勾股定理可得:
(米)
答:至少需要10米长的梯子。
课堂小结:
1.知识内容:勾股定理
2.题目类型:在直角三角形中,已知两边,求第三边。
3.思想方法:(1)数形结合思想
(2)面积分割法
作业:
A组:P69 1、2、4
B组:P70 7、8
C组:P71 11
必做题(任选一组):
18.1 勾股定理
第二十四届国际数学家大会
为什么选这个图形作会徽呢?
会 徽
18.1 勾股定理
股
勾
弦
什么是勾?什么是股?
在直角三角形中,
较短的直角边——勾
较长的直角边——股
斜 边 ——弦
勾股定理的对象是——直角三角形的三条边。
活动1. 生活中处处都有数学
活动2. 这条规律也适用于 一般的直角三角形吗?
活动3: 你能证明命题是正确的吗?
活动4: 原来就是你
毕达哥拉斯
勾股定理 = 毕达哥拉斯定理
我们也来观察一下吧!
毕达哥拉斯
他朋友家的地板
他眼中的地板
三个正方形的面积有某种数量关系
活动1. 生活中处处都有数学
单位面积
A
C
A
B
1.正方形A中含有( )个小直角三角形,A的面积是( )个单位面积;
2.正方形B中含有 ( )个小直角三角形,B的面积是( )个单位面积;
3.正方形C中含有( )个小直角三角形,C的面积是( )个单位面积;
单位面积
2
2
4
1
(每个小等腰直角三角形的面积都是 个单位面积)
C
A
B
图1-1
图1-2
1.A的面积是 ( ) 个单位面积;
2.B的面积是( )个单位面积;
3.C的面积是( )个单位面积。
A
B
C
再观察一下图形2:
a
b
c
2
2
4
(每个小等腰直角三角形的面积都是 个单位面积)
正方形A的面积
正方形B的面积
正方形C的面积
图1-1
图1-2
A、B、C的面积关系
等腰直角三角形三边关系
1
2
2
4
A的面积 + B的面积 = C的面积
两直角边的平方和等于斜边的平方
利用图1和图2收集的数据,补充下表:
因此可知等腰直角三角形有这样的性质:
两直角边的平方和等于斜边的平方
A
B
C
图1-3
A
B
C
图1-4
活动2. 这条规律也适用于 一般的直角三角形吗?(每个方格都是单位面积)
A的面积 B的面积 C的面积
图3
图4
A、B、C面积关系
直角三角形三边关系
16
9
4
9
?
?
如何求正方形C的面积呢?
面积分割法:
正方形C的面积
= 4个三角形的面积 +
小正方形的面积
A
B
C
图1-3
A
B
C
图1-4
命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。
c
a
b
由活动1和活动2,我们得到:
你能利用这个图来证明吗?
这个图是1700多年前我国古人赵爽证明这个规律时给出的,所以被称为“赵爽弦图”。
活动3:你能证明命题1是正确的吗?
思想相同
分割面积法
A
B
C
图1-3
A
B
C
图1-4
a
b
c
b
c
a
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
a
b
c
赵爽弦图
b-a
证明:
活动四:原来就是你
命题1被证明是正确的!
正确的命题称为定理。
命题 1
勾股定理
勾股定理:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。
实战演练
例1.在三角形ABC中,角C为直角,
(1)已知b=6,c=10,求a.
(2)已知a=15, b=20,求c.
A
C
B
例1.在三角形ABC中,角C为直角,
(1)已知b=6,c=10,求a.
(2)已知a=15, b=20,求c.
实战演练
解:(1)由勾股定理可得:
(2)由勾股定理可得:
C
A
B
例2.要登上8米高的建筑物BC,为了安全,需使梯子底端离
建筑物的距离AB为6米,问至少需要多长的梯子?
例2.要登上8米高的建筑物BC,为了安全,需使梯子底端离
建筑物的距离AB为6米,问至少需要多长的梯子?
解:由题可知,
为直角三角形,
且
由勾股定理可得:
(米)
答:至少需要10米长的梯子。
课堂小结:
1.知识内容:勾股定理
2.题目类型:在直角三角形中,已知两边,求第三边。
3.思想方法:(1)数形结合思想
(2)面积分割法
作业:
A组:P69 1、2、4
B组:P70 7、8
C组:P71 11
必做题(任选一组):
