2021年上海市徐汇高一(下)期中考试数学试卷(2021.04) (图片版 含答案)
文档属性
| 名称 | 2021年上海市徐汇高一(下)期中考试数学试卷(2021.04) (图片版 含答案) |  | |
| 格式 | |||
| 文件大小 | 522.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-21 15:52:30 | ||
图片预览

文档简介
徐汇中学高一期中数学试卷
2021.04
填空题
1.点P从圆心在原点O的单位圆上点(0)出发,沿顺时针方向运动x弧长,到达点Q
则点Q的坐标是
2.已知角a满足sina+cosa
则tana+cota的值为
3.已知角a终边上有一点P(4,3),则sin(a+)
4.已知f(x)=x2-1,则f-(3)
5.若函数y=2sinx+√
a
cosx的最大值为3,则a的值为
6.△ABC中,
bcos
a=
acos
B,则此三角形的形状为
7.函数f(x)
函数(填奇或偶)
8.如图所示,电视塔DC,在地面上一点A测得电视塔尖C
的仰角是
再向塔底方向前进100米到达点B,此时测
得电视塔尖C的仰角为60
电视塔的高度是
精确到0.米)
3
9.已知cos(a+B)cosa+sin(a+f)sina
则cos2B=
10.函数f(x)=sinx+sin(x-)图像的对称轴方程为
11.设a1,a2∈R,且
=2021,则tan(a1+a2)
2+sina,
2+sin(2a,)
12.平面直角坐标系中,将函数y=f(x),x∈D上满足x∈N,y∈N的点P(x,y),称
为函数的“正格点”,若函数∫(x)=
Sin
mx,x∈R,m∈(,2)与函数g(x)=lgx的图像
存在正格点交点,则这两个函数图像的所有交点个数为
选择题
“tanx=0”是“x=0”成立的()条件
A.充分非必要
B.必要非充分C.充要
D.既非充分又非必要
14.函数y=sinx-|sinx的值域是
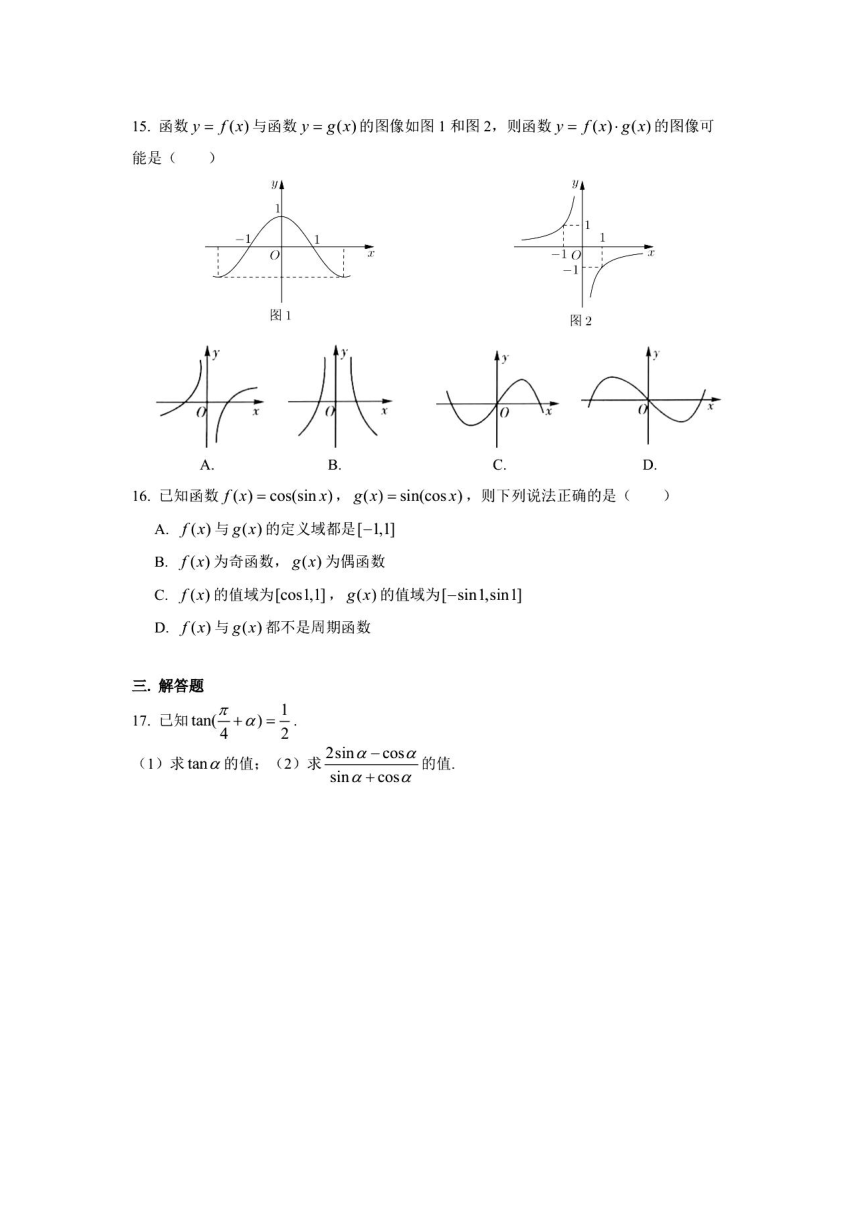
B.[-2,2
15.函数y=f(x)与函数y=g(x)的图像如图1和图2,则函数y=f(x)·g(x)的图像可
能是()
16.已知函数f(x)=cos(sinx),g(x)=sin(cosx),则下列说法正确的是(
A.f(x)与g(x)的定义域都是[-1,1
f(x)为奇函数,g(x)为偶函数
C.∫(x)的值域为[cosl,1],g(x)的值域为[-sinl,sinl
D.f(x)与g(x)都不是周期函数
7.已知tmn(+a)
1)求tana的值;(2)求
的值
sin
a
+
cos
a
已知函数f(x)=2√3
sInrcosr+2sin2x-
(1)求函数f(x)的最小正周期
(2)求函数f(x)在x∈[0,。]上的值域
19.△ABC中,A=60°,a=√3
(1)若b=2,求C;
(2)求三角形面积的最大值
20.某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点O为圆心的两个同心圆
弧AD、弧BC以及两条线段AB和CD围成的封闭图形,花坛设计周长为30米,其中大圆
弧AD所在圆的半径为10米,设小圆弧BC所在圆的半径为x米(0弧度
(1)求θ关于x的函数关系式;
(2)在装饰花坛边缘时,两条直线段的装饰费用为4元/米,两条弧线部分的装饰费用为9
元米,设花坛的面积与装饰总费用的比为y,当x为何值时,y取得最大值?
2021.04
填空题
1.点P从圆心在原点O的单位圆上点(0)出发,沿顺时针方向运动x弧长,到达点Q
则点Q的坐标是
2.已知角a满足sina+cosa
则tana+cota的值为
3.已知角a终边上有一点P(4,3),则sin(a+)
4.已知f(x)=x2-1,则f-(3)
5.若函数y=2sinx+√
a
cosx的最大值为3,则a的值为
6.△ABC中,
bcos
a=
acos
B,则此三角形的形状为
7.函数f(x)
函数(填奇或偶)
8.如图所示,电视塔DC,在地面上一点A测得电视塔尖C
的仰角是
再向塔底方向前进100米到达点B,此时测
得电视塔尖C的仰角为60
电视塔的高度是
精确到0.米)
3
9.已知cos(a+B)cosa+sin(a+f)sina
则cos2B=
10.函数f(x)=sinx+sin(x-)图像的对称轴方程为
11.设a1,a2∈R,且
=2021,则tan(a1+a2)
2+sina,
2+sin(2a,)
12.平面直角坐标系中,将函数y=f(x),x∈D上满足x∈N,y∈N的点P(x,y),称
为函数的“正格点”,若函数∫(x)=
Sin
mx,x∈R,m∈(,2)与函数g(x)=lgx的图像
存在正格点交点,则这两个函数图像的所有交点个数为
选择题
“tanx=0”是“x=0”成立的()条件
A.充分非必要
B.必要非充分C.充要
D.既非充分又非必要
14.函数y=sinx-|sinx的值域是
B.[-2,2
15.函数y=f(x)与函数y=g(x)的图像如图1和图2,则函数y=f(x)·g(x)的图像可
能是()
16.已知函数f(x)=cos(sinx),g(x)=sin(cosx),则下列说法正确的是(
A.f(x)与g(x)的定义域都是[-1,1
f(x)为奇函数,g(x)为偶函数
C.∫(x)的值域为[cosl,1],g(x)的值域为[-sinl,sinl
D.f(x)与g(x)都不是周期函数
7.已知tmn(+a)
1)求tana的值;(2)求
的值
sin
a
+
cos
a
已知函数f(x)=2√3
sInrcosr+2sin2x-
(1)求函数f(x)的最小正周期
(2)求函数f(x)在x∈[0,。]上的值域
19.△ABC中,A=60°,a=√3
(1)若b=2,求C;
(2)求三角形面积的最大值
20.某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点O为圆心的两个同心圆
弧AD、弧BC以及两条线段AB和CD围成的封闭图形,花坛设计周长为30米,其中大圆
弧AD所在圆的半径为10米,设小圆弧BC所在圆的半径为x米(0
(1)求θ关于x的函数关系式;
(2)在装饰花坛边缘时,两条直线段的装饰费用为4元/米,两条弧线部分的装饰费用为9
元米,设花坛的面积与装饰总费用的比为y,当x为何值时,y取得最大值?
同课章节目录
