人教版八年级下册同步练习20.1.2 第2课时 平均数、中位数、众数的综合应用(word版含答案)
文档属性
| 名称 | 人教版八年级下册同步练习20.1.2 第2课时 平均数、中位数、众数的综合应用(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 163.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-22 11:34:44 | ||
图片预览



文档简介
20.1.2
第2课时 平均数、中位数、众数的综合应用
知识点
1 平均数、众数、中位数之间的计算
1.2019·雅安已知一组数据5,4,x,3,9的平均数为5,则这组数据的中位数是( )
A.3
B.4
C.5
D.6
2.一组按从小到大的顺序排列的数据:a,3,4,4,6(a为正整数),唯一的众数是4,则该组数据的平均数是( )
A.3.6
B.3.8
C.3.6或3.8
D.4.2
3.五名学生投篮球,规定每人投20次,统计他们每人投中的次数,得到五个数据.若这五个数据的中位数是6,唯一众数是7,则他们投中次数的总和可能是( )
A.20
B.28
C.30
D.31
4.2019·十堰一次数学测试中,某小组5名同学的成绩(单位:分)统计如下表(有两个数据被遮盖):
组员
甲
乙
丙
丁
戊
平均成绩
众数
得分
81
77
■
80
82
80
■
则被遮盖的两个数据依次是( )
A.80,80
B.81,80
C.80,2
D.81,2
5.已知一组从小到大排列的数据2,5,x,y,2x,11的平均数与中位数都是7,则这组数据的众数是________.
6.一个样本数据为1,3,2,2,a,b,c,已知这个样本数据的众数为3,平均数为2,则这组数据的中位数为________.
7.两组数据3,5,2a,b与b,6,a的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数和众数分别为________.
知识点
2 平均数、众数、中位数三个统计量的选择与判断
8.某工艺品厂共有16名工人,调查每名工人的日均生产能力,获得如下数据:
日均生产能力(件)
10
11
12
13
14
15
人数
1
3
5
4
2
1
(1)求这16名工人日均生产件数的平均数、众数、中位数;
(2)若要使75%的工人都能完成任务,应选什么统计量(平均数、众数、中位数)作为日生产件数的定额?
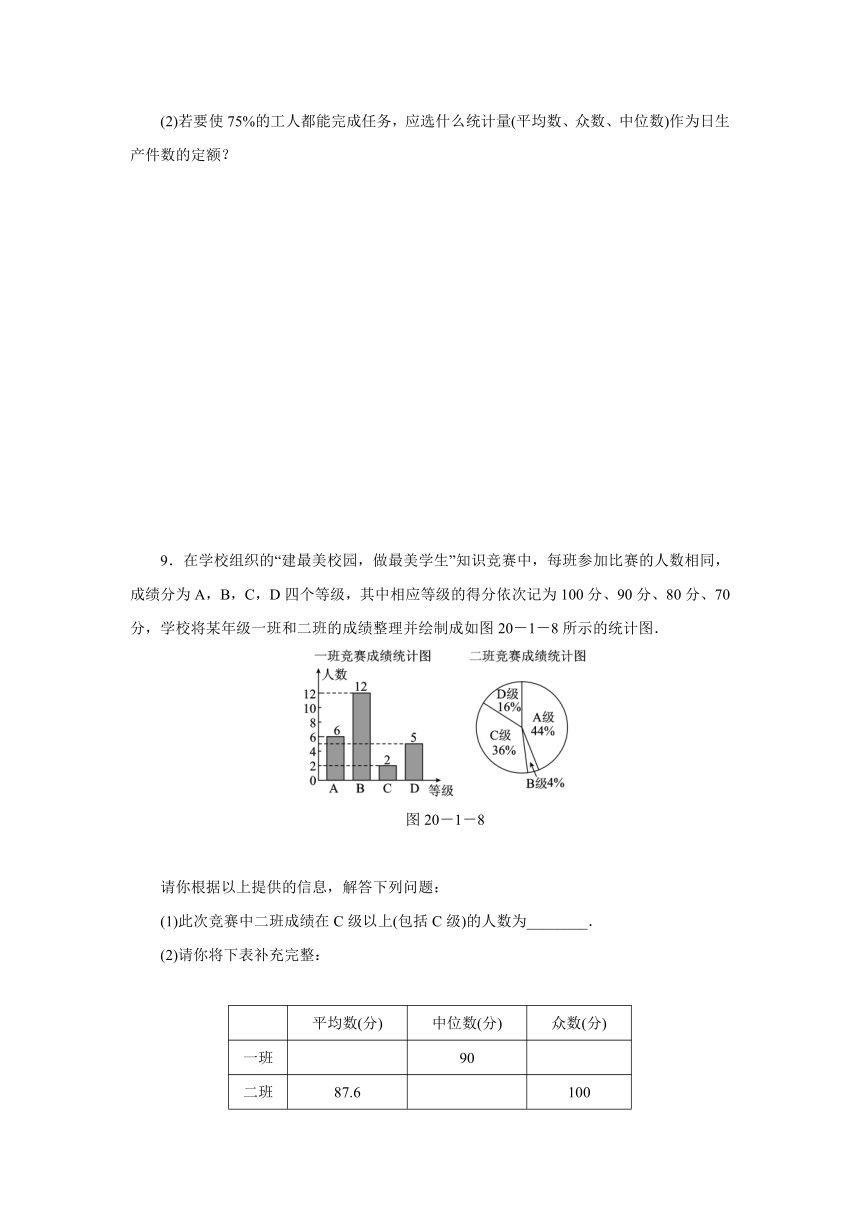
9.在学校组织的“建最美校园,做最美学生”知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级一班和二班的成绩整理并绘制成如图20-1-8所示的统计图.
图20-1-8
请你根据以上提供的信息,解答下列问题:
(1)此次竞赛中二班成绩在C级以上(包括C级)的人数为________.
(2)请你将下表补充完整:
平均数(分)
中位数(分)
众数(分)
一班
90
二班
87.6
100
(3)请你从下列不同角度对这次竞赛成绩的结果进行分析.
①从平均数和中位数的角度来比较一班和二班的成绩;
②从平均数和众数的角度来比较一班和二班的成绩;
③从B级以上(包括B级)的人数的角度来比较一班和二班的成绩.
10.某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
30
16
14
15
26
15
32
23
17
15
15
28
28
16
19
17
18
16
13
24
15
28
26
18
19
22
17
16
19
32
整理上面的数据,得到下面两个不完整的统计表:
频数分布表
组别
一
二
三
四
五
六
七
销售额
13≤
x<16
16≤
x<19
19≤
x<22
22≤
x<25
25≤
x<28
28≤
x<31
31≤
x<34
频数
7
9
a
3
2
4
b
数据分析表
平均数(万元)
众数(万元)
中位数(万元)
20.3
c
d
请根据以上信息,解答下列问题:
(1)填空:a=________,b=______,c=______,d=________;
(2)若将月销售额不低于22万元确定为销售目标,则有________位营业员可以获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少比较合适?说明理由.
能力拓展提升
11.八年级一班邀请A,B,C,D,E五位评委对甲、乙两名同学的才艺表演打分,并组织全班50名同学对两人进行民主测评投票,绘制了如下统计表和不完整的条形统计图(如图20-1-9).
并求得了五位评委对甲同学才艺表演所打分数的平均数和中位数:
==90.6(分);中位数是91分.
(1)求五位评委对乙同学才艺表演所打分数的平均数和中位数.
(2)a=________,并补全条形统计图.
(3)为了从甲、乙二人中只选拔出一人去参加艺术节演出,班级制定了如下的选拔规则:选拔综合分数最高的同学参加艺术节演出,其中:
综合分=才艺分×k+测评分×(1-k)(0.4才艺分=五位评委所打分数中去掉一个最高分和一个最低分,再算平均分;
测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
①当k=0.6时,通过计算说明应选拔哪名同学去参加艺术节演出;
②通过计算说明k的值不能是多少.
五位评委的打分表(单位:分)
A
B
C
D
E
甲
89
91
93
94
86
乙
88
87
90
98
92
图20-1-9
典题讲评与答案详析
1.B
2.C [解析]
因为数据a,3,4,4,6(a为正整数)的唯一的众数是4,
所以a=1或a=2.
当a=1时,平均数为=3.6;
当a=2时,平均数为=3.8.
3.B [解析]
最大的三个数的和是6+7+7=20,两个较小的数一定是小于6的非负整数,且不相等,则五个数的和一定大于20且小于等于29.显然只有选项B符合题意.
4.A [解析]
根据题意,得80×5-(81+77+80+82)=80(分),则丙的得分是80分,众数是80分.
5.5 [解析]
因为一组从小到大排列的数据2,5,x,y,2x,11的平均数与中位数都是7,
所以(2+5+x+y+2x+11)=(x+y)=7,解得y=9,x=5,所以这组数据的众数是5.
6.2 [解析]
因为平均数=(1+3+2+2+a+b+c)=2,所以a+b+c=6.因为众数为3,所以a,b,c中必有两个数为3,不妨设a=b=3,则有c=0.将数据按从小到大的顺序排列后,位于最中间的一个数是2,所以中位数是2.
7.6,8 [解析]
根据题意,得
解得则两组数据合并为一组数据后为3,4,5,6,8,8,8,所以这组新数据的中位数为6,众数为8.
8.解:(1)由表格可得平均数是
=12.375(件),众数是12件,中位数是12件.
(2)选中位数或众数作为日生产件数的定额.
9.解:(1)由条形统计图可知一班参加比赛的人数有6+12+2+5=25(人).
因为两班的参赛人数相同,
所以二班参加比赛的人数为25,
所以此次竞赛中二班成绩在C级以上(包括C级)的人数为25×(1-16%)=21.
(2)一班成绩的平均数为(6×100+12×90+2×80+5×70)÷25=87.6(分);一班成绩的众数是90分;二班成绩的中位数是80分.
(3)①一班和二班成绩的平均数相同,一班成绩的中位数高,所以一班成绩好.
②一班和二班成绩的平均数相同,二班成绩的众数高,说明二班的高分人数多,所以二班成绩好.
③一班成绩在B级以上(包括B级)的有18人,二班成绩在B级以上(包括B级)的有12人,所以一班成绩好.
10.解:(1)3 2 15 18
(2)11
(3)月销售额定为18万元比较合适.
理由:18万元是所统计月销售额的中位数,月销售额低于18万元和超过18万元的人数相同,均为14人,所以月销售额定为18万元比较合适.
11.解:(1)==91(分);中位数是90分.
(2)a=50-40-2=8,补全条形统计图如图.
(3)①甲的才艺分==91(分),
甲的测评分=40×2+8×1+2×0=88(分),
甲的综合分=91×0.6+88×(1-0.6)=89.8(分);
乙的才艺分==90(分),
乙的测评分=42×2+5×1+3×0=89(分),
乙的综合分=90×0.6+89×(1-0.6)=89.6(分).
因为甲的综合分>乙的综合分,
所以应选拔甲同学去参加艺术节演出.
②甲的综合分=91k+88(1-k)=(3k+88)分,
乙的综合分=90k+89(1-k)=(k+89)分,
若从甲、乙二人中只选拔出一人去参加演出,
则3k+88≠k+89,解得k≠0.5.
故k的值不能是0.5.
第2课时 平均数、中位数、众数的综合应用
知识点
1 平均数、众数、中位数之间的计算
1.2019·雅安已知一组数据5,4,x,3,9的平均数为5,则这组数据的中位数是( )
A.3
B.4
C.5
D.6
2.一组按从小到大的顺序排列的数据:a,3,4,4,6(a为正整数),唯一的众数是4,则该组数据的平均数是( )
A.3.6
B.3.8
C.3.6或3.8
D.4.2
3.五名学生投篮球,规定每人投20次,统计他们每人投中的次数,得到五个数据.若这五个数据的中位数是6,唯一众数是7,则他们投中次数的总和可能是( )
A.20
B.28
C.30
D.31
4.2019·十堰一次数学测试中,某小组5名同学的成绩(单位:分)统计如下表(有两个数据被遮盖):
组员
甲
乙
丙
丁
戊
平均成绩
众数
得分
81
77
■
80
82
80
■
则被遮盖的两个数据依次是( )
A.80,80
B.81,80
C.80,2
D.81,2
5.已知一组从小到大排列的数据2,5,x,y,2x,11的平均数与中位数都是7,则这组数据的众数是________.
6.一个样本数据为1,3,2,2,a,b,c,已知这个样本数据的众数为3,平均数为2,则这组数据的中位数为________.
7.两组数据3,5,2a,b与b,6,a的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数和众数分别为________.
知识点
2 平均数、众数、中位数三个统计量的选择与判断
8.某工艺品厂共有16名工人,调查每名工人的日均生产能力,获得如下数据:
日均生产能力(件)
10
11
12
13
14
15
人数
1
3
5
4
2
1
(1)求这16名工人日均生产件数的平均数、众数、中位数;
(2)若要使75%的工人都能完成任务,应选什么统计量(平均数、众数、中位数)作为日生产件数的定额?
9.在学校组织的“建最美校园,做最美学生”知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级一班和二班的成绩整理并绘制成如图20-1-8所示的统计图.
图20-1-8
请你根据以上提供的信息,解答下列问题:
(1)此次竞赛中二班成绩在C级以上(包括C级)的人数为________.
(2)请你将下表补充完整:
平均数(分)
中位数(分)
众数(分)
一班
90
二班
87.6
100
(3)请你从下列不同角度对这次竞赛成绩的结果进行分析.
①从平均数和中位数的角度来比较一班和二班的成绩;
②从平均数和众数的角度来比较一班和二班的成绩;
③从B级以上(包括B级)的人数的角度来比较一班和二班的成绩.
10.某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
30
16
14
15
26
15
32
23
17
15
15
28
28
16
19
17
18
16
13
24
15
28
26
18
19
22
17
16
19
32
整理上面的数据,得到下面两个不完整的统计表:
频数分布表
组别
一
二
三
四
五
六
七
销售额
13≤
x<16
16≤
x<19
19≤
x<22
22≤
x<25
25≤
x<28
28≤
x<31
31≤
x<34
频数
7
9
a
3
2
4
b
数据分析表
平均数(万元)
众数(万元)
中位数(万元)
20.3
c
d
请根据以上信息,解答下列问题:
(1)填空:a=________,b=______,c=______,d=________;
(2)若将月销售额不低于22万元确定为销售目标,则有________位营业员可以获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少比较合适?说明理由.
能力拓展提升
11.八年级一班邀请A,B,C,D,E五位评委对甲、乙两名同学的才艺表演打分,并组织全班50名同学对两人进行民主测评投票,绘制了如下统计表和不完整的条形统计图(如图20-1-9).
并求得了五位评委对甲同学才艺表演所打分数的平均数和中位数:
==90.6(分);中位数是91分.
(1)求五位评委对乙同学才艺表演所打分数的平均数和中位数.
(2)a=________,并补全条形统计图.
(3)为了从甲、乙二人中只选拔出一人去参加艺术节演出,班级制定了如下的选拔规则:选拔综合分数最高的同学参加艺术节演出,其中:
综合分=才艺分×k+测评分×(1-k)(0.4
测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
①当k=0.6时,通过计算说明应选拔哪名同学去参加艺术节演出;
②通过计算说明k的值不能是多少.
五位评委的打分表(单位:分)
A
B
C
D
E
甲
89
91
93
94
86
乙
88
87
90
98
92
图20-1-9
典题讲评与答案详析
1.B
2.C [解析]
因为数据a,3,4,4,6(a为正整数)的唯一的众数是4,
所以a=1或a=2.
当a=1时,平均数为=3.6;
当a=2时,平均数为=3.8.
3.B [解析]
最大的三个数的和是6+7+7=20,两个较小的数一定是小于6的非负整数,且不相等,则五个数的和一定大于20且小于等于29.显然只有选项B符合题意.
4.A [解析]
根据题意,得80×5-(81+77+80+82)=80(分),则丙的得分是80分,众数是80分.
5.5 [解析]
因为一组从小到大排列的数据2,5,x,y,2x,11的平均数与中位数都是7,
所以(2+5+x+y+2x+11)=(x+y)=7,解得y=9,x=5,所以这组数据的众数是5.
6.2 [解析]
因为平均数=(1+3+2+2+a+b+c)=2,所以a+b+c=6.因为众数为3,所以a,b,c中必有两个数为3,不妨设a=b=3,则有c=0.将数据按从小到大的顺序排列后,位于最中间的一个数是2,所以中位数是2.
7.6,8 [解析]
根据题意,得
解得则两组数据合并为一组数据后为3,4,5,6,8,8,8,所以这组新数据的中位数为6,众数为8.
8.解:(1)由表格可得平均数是
=12.375(件),众数是12件,中位数是12件.
(2)选中位数或众数作为日生产件数的定额.
9.解:(1)由条形统计图可知一班参加比赛的人数有6+12+2+5=25(人).
因为两班的参赛人数相同,
所以二班参加比赛的人数为25,
所以此次竞赛中二班成绩在C级以上(包括C级)的人数为25×(1-16%)=21.
(2)一班成绩的平均数为(6×100+12×90+2×80+5×70)÷25=87.6(分);一班成绩的众数是90分;二班成绩的中位数是80分.
(3)①一班和二班成绩的平均数相同,一班成绩的中位数高,所以一班成绩好.
②一班和二班成绩的平均数相同,二班成绩的众数高,说明二班的高分人数多,所以二班成绩好.
③一班成绩在B级以上(包括B级)的有18人,二班成绩在B级以上(包括B级)的有12人,所以一班成绩好.
10.解:(1)3 2 15 18
(2)11
(3)月销售额定为18万元比较合适.
理由:18万元是所统计月销售额的中位数,月销售额低于18万元和超过18万元的人数相同,均为14人,所以月销售额定为18万元比较合适.
11.解:(1)==91(分);中位数是90分.
(2)a=50-40-2=8,补全条形统计图如图.
(3)①甲的才艺分==91(分),
甲的测评分=40×2+8×1+2×0=88(分),
甲的综合分=91×0.6+88×(1-0.6)=89.8(分);
乙的才艺分==90(分),
乙的测评分=42×2+5×1+3×0=89(分),
乙的综合分=90×0.6+89×(1-0.6)=89.6(分).
因为甲的综合分>乙的综合分,
所以应选拔甲同学去参加艺术节演出.
②甲的综合分=91k+88(1-k)=(3k+88)分,
乙的综合分=90k+89(1-k)=(k+89)分,
若从甲、乙二人中只选拔出一人去参加演出,
则3k+88≠k+89,解得k≠0.5.
故k的值不能是0.5.
