人教版八年级下册同步练习20.3 课题学习 体质健康测试中的数据分析(word版含答案)
文档属性
| 名称 | 人教版八年级下册同步练习20.3 课题学习 体质健康测试中的数据分析(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 769.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-22 00:00:00 | ||
图片预览


文档简介
20.3 课题学习 体质健康测试中的数据分析
1.在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A.众数
B.中位数
C.平均数
D.方差
2.有二十二位同学参加智力竞赛,他们的分数互不相同,按分数高低选十一位同学进入下一轮比赛,小明知道了自己的分数后,还需知道哪个统计量,就能判断自己能否进入下一轮比赛( )
A.中位数
B.众数
C.方差
D.平均数
3.为了了解我市某学校“书香校园”的建设情况,检查组在该校随机抽取40名学生,调查了解他们一周课外阅读的时间,并将调查结果绘制成如图所示的频数分布直方图(每小组的时间包含最小值,不包含最大值),根据图中信息估计该校学生一周课外阅读时间不少于4h的人数占全校人数的百分数约为(
)
A.50%
B.55%
C.60%
D.65%
4.如图是根据某地4月上旬每天最低气温绘成的折线图,那么这段时间最低气温的极差、众数、平均数依次是(
).
A.5°
5°
4°
B.5°
5°
4.5°
C.2.8°
5°
4°
D.2.8°
5°
4.5°
5.已知甲、乙两组数据的平均数都是5,甲组数据的方差=,乙组数据的方差=,那么下列说法正确的是(
).
A.甲组数据比乙组数据的波动大
B.乙组数据比甲组数据的波动大
C.甲组数据与乙组数据的波动一样大
D.甲、乙两组数据的波动大小不能比较
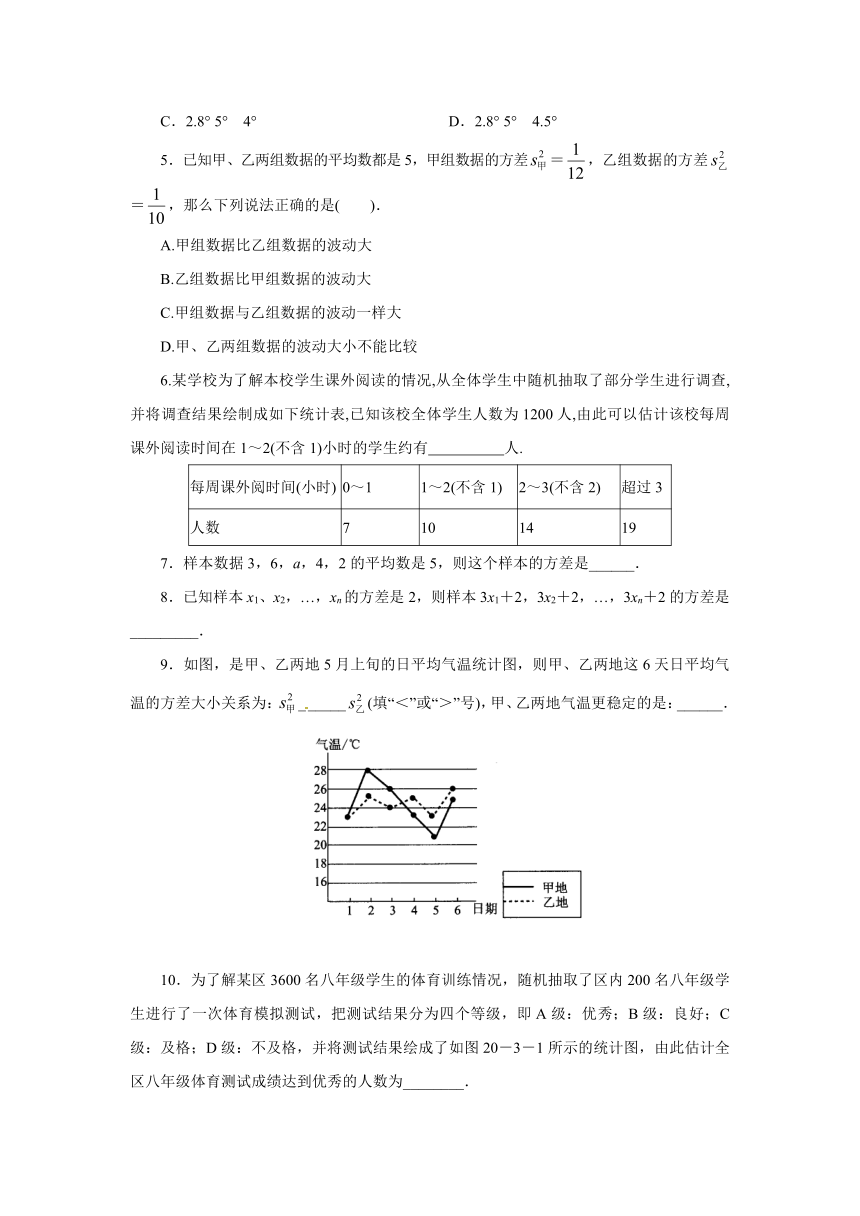
6.某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下统计表,已知该校全体学生人数为1200人,由此可以估计该校每周课外阅读时间在1~2(不含1)小时的学生约有
人.
每周课外阅时间(小时)
0~1
1~2(不含1)
2~3(不含2)
超过3
人数
7
10
14
19
7.样本数据3,6,a,4,2的平均数是5,则这个样本的方差是______.
8.已知样本x1、x2,…,xn的方差是2,则样本3x1+2,3x2+2,…,3xn+2的方差是_________.
9.如图,是甲、乙两地5月上旬的日平均气温统计图,则甲、乙两地这6天日平均气温的方差大小关系为:______(填“<”或“>”号),甲、乙两地气温更稳定的是:______.
10.为了解某区3600名八年级学生的体育训练情况,随机抽取了区内200名八年级学生进行了一次体育模拟测试,把测试结果分为四个等级,即A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘成了如图20-3-1所示的统计图,由此估计全区八年级体育测试成绩达到优秀的人数为________.
图20-3-1
11.某校为了更好地开展“学校特色体育教育”,从全校八年级各班随机抽取了60名学生进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据得到的关于每个个体的测试成绩的部分统计表:
某校60名学生体育测试成绩频数分布表
成绩
划记
频数
百分比
优秀
正正正
a
0.3
良好
正正正正正正
30
b
合格
正
9
0.15
不合格
c
d
合计
(说明:40~55分为不合格,55~70分为合格,70~85分为良好,85~100分为优秀,各分组包括最大值,不包括最小值)
请根据以上信息,解答下列问题:
(1)填空:a=________,b=________,c=________,d=________;
(2)请根据频数分布表,画出相应的频数分布直方图;
(3)这一组数据的中位数落在__________组.
A.40~55分
B.55~70分
C.70~85分
D.85~100分
12.国家规定体质健康状况分为优秀、良好、合格和不合格四种等级.为了了解某地区10000名初中学生的体质健康状况,某校数学兴趣小组从该地区七、八、九年级随机抽取了共500名学生的数据进行整理分析,他们对其中体质健康为优秀的人数做了如图20-3-2所示的分析.
(1)本次随机抽取的七年级人数m=________;
(2)补全条形统计图;
(3)根据抽样调查的结果,估计该地区10000名初中生体质健康状况为优秀的人数.
图20-3-2
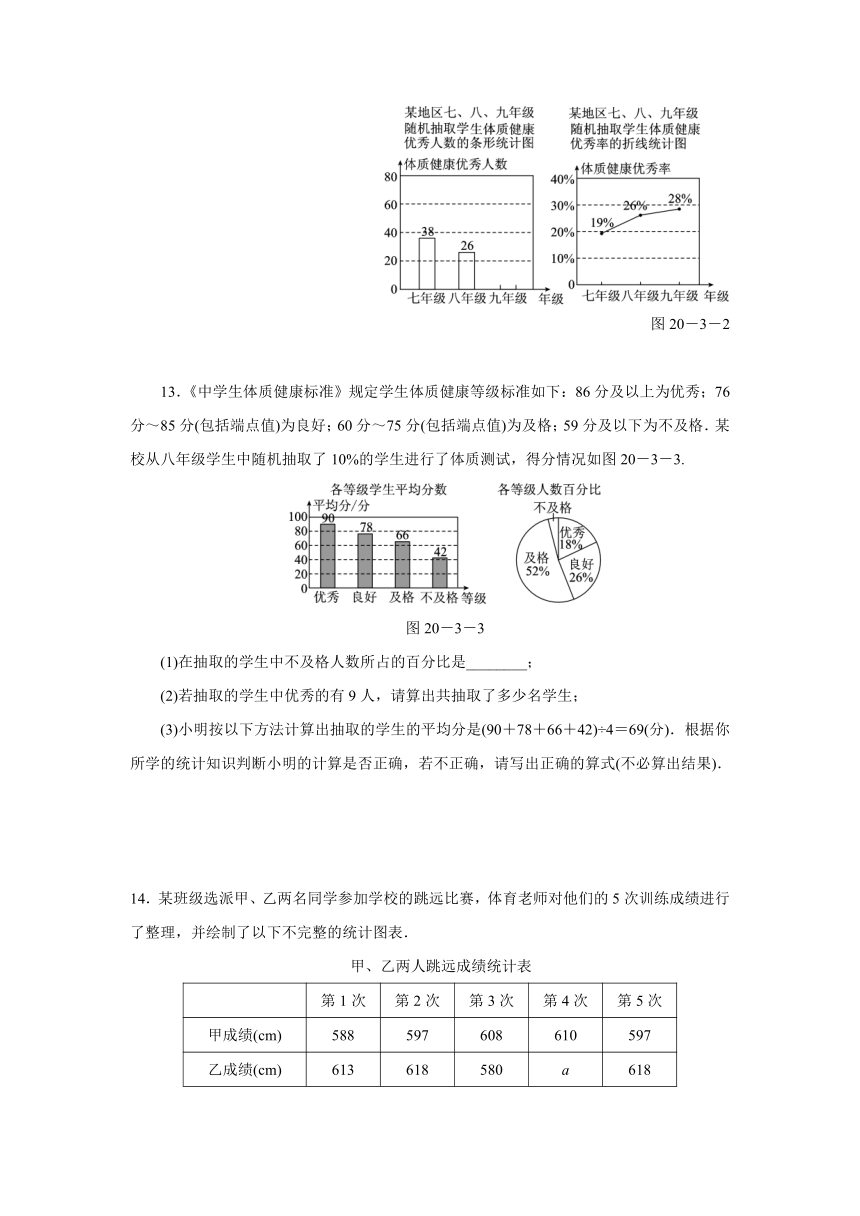
13.《中学生体质健康标准》规定学生体质健康等级标准如下:86分及以上为优秀;76分~85分(包括端点值)为良好;60分~75分(包括端点值)为及格;59分及以下为不及格.某校从八年级学生中随机抽取了10%的学生进行了体质测试,得分情况如图20-3-3.
图20-3-3
(1)在抽取的学生中不及格人数所占的百分比是________;
(2)若抽取的学生中优秀的有9人,请算出共抽取了多少名学生;
(3)小明按以下方法计算出抽取的学生的平均分是(90+78+66+42)÷4=69(分).根据你所学的统计知识判断小明的计算是否正确,若不正确,请写出正确的算式(不必算出结果).
14.某班级选派甲、乙两名同学参加学校的跳远比赛,体育老师对他们的5次训练成绩进行了整理,并绘制了以下不完整的统计图表.
甲、乙两人跳远成绩统计表
第1次
第2次
第3次
第4次
第5次
甲成绩(cm)
588
597
608
610
597
乙成绩(cm)
613
618
580
a
618
图20-3-4
根据以上信息,请解答下列问题:
(1)a=________;
(2)请完成图中表示甲成绩变化情况的折线;
(3)通过计算,补全下面的统计分析表:
最好的成绩(cm)
平均数(cm)
众数(cm)
方差
甲
597
65.2
乙
618
600.6
378.24
(4)请依据(3)中所统计的数据,分析甲、乙两名同学的训练成绩各有什么特点.
典题讲评与答案详析
1.【答案】B
【解析】由于总共有9个人,且他们的分数互不相同,第5的成绩是中位数,要判断是否进入前5名,故应知道中位数的多少.
故选:B.
2.【答案】A
【解析】因为有二十二位同学参加,选十一位同学进入下一轮比赛,那么分数从高到低排列后,第11名和第12名的平均的分数就是中位数,所以小明知道自己的分数和中位数后,才能判断自己能否进入下一轮比赛.
故选A.
3.C
解析
由题图,得m=40-5-11-4=20,则该校学生一周课外阅读时间不少于4h的人数占全校人数的百分数约为(20+4)÷4×100%=60%.故选C.
4.B.
5.B.
6.240
解析
先求出样本数据中每周课外阅读时间在1~2(不含1)小时的学生人数的频率,然后再用此频率估算该校每周课外阅读时间在1~2(不含1)小时的学生数即可.
该校每周课外阅读时间在1~2(不含1)小时的学生有1200×=1200×=240(人).
7.8.
8.18.
9.>,乙.
10.360 [解析]
九年级体育测试成绩可以达到优秀的人数约为3600×(1-30%-35%-25%)=360.
11.解:(1)18 0.5 3 0.05
(2)频数分布直方图如图所示.
(3)C
12.解:(1)本次随机抽取的七年级人数m=38÷19%=200.故答案为200.
(2)本次随机抽取的八年级人数为26÷26%=100,
则本次随机抽取的九年级人数为500-200-100=200,
则九年级体质健康为优秀的人数为200×28%=56.
补全条形统计图如图.
某地区七、八、九年级随机抽取学生体质
健康优秀人数的条形统计图
(3)×10000=2400(人).
答:估计该地区10000名初中生体质健康状况为优秀的人数是2400人.
13.解:(1)不及格人数所占的百分比是1-52%-18%-26%=4%.
故答案为4%.
(2)9÷18%=50(名).
答:共抽取了50名学生.
(3)不正确.
正确的算式:
90×18%+78×26%+66×52%+42×4%.
14.解:(1)由折线统计图可知,a=574.
(2)如图所示.
(3)填表如下:
最好的成
绩(cm)
平均数
(cm)
众数(cm)
方差
甲
610
600
597
65.2
乙
618
600.6
618
378.24
(4)从最好的成绩、平均数、众数的角度来看,乙的训练成绩优于甲的训练成绩;
从方差的角度来看,甲的方差小,说明甲的训练成绩比乙的训练成绩稳定.
1.在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A.众数
B.中位数
C.平均数
D.方差
2.有二十二位同学参加智力竞赛,他们的分数互不相同,按分数高低选十一位同学进入下一轮比赛,小明知道了自己的分数后,还需知道哪个统计量,就能判断自己能否进入下一轮比赛( )
A.中位数
B.众数
C.方差
D.平均数
3.为了了解我市某学校“书香校园”的建设情况,检查组在该校随机抽取40名学生,调查了解他们一周课外阅读的时间,并将调查结果绘制成如图所示的频数分布直方图(每小组的时间包含最小值,不包含最大值),根据图中信息估计该校学生一周课外阅读时间不少于4h的人数占全校人数的百分数约为(
)
A.50%
B.55%
C.60%
D.65%
4.如图是根据某地4月上旬每天最低气温绘成的折线图,那么这段时间最低气温的极差、众数、平均数依次是(
).
A.5°
5°
4°
B.5°
5°
4.5°
C.2.8°
5°
4°
D.2.8°
5°
4.5°
5.已知甲、乙两组数据的平均数都是5,甲组数据的方差=,乙组数据的方差=,那么下列说法正确的是(
).
A.甲组数据比乙组数据的波动大
B.乙组数据比甲组数据的波动大
C.甲组数据与乙组数据的波动一样大
D.甲、乙两组数据的波动大小不能比较
6.某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下统计表,已知该校全体学生人数为1200人,由此可以估计该校每周课外阅读时间在1~2(不含1)小时的学生约有
人.
每周课外阅时间(小时)
0~1
1~2(不含1)
2~3(不含2)
超过3
人数
7
10
14
19
7.样本数据3,6,a,4,2的平均数是5,则这个样本的方差是______.
8.已知样本x1、x2,…,xn的方差是2,则样本3x1+2,3x2+2,…,3xn+2的方差是_________.
9.如图,是甲、乙两地5月上旬的日平均气温统计图,则甲、乙两地这6天日平均气温的方差大小关系为:______(填“<”或“>”号),甲、乙两地气温更稳定的是:______.
10.为了解某区3600名八年级学生的体育训练情况,随机抽取了区内200名八年级学生进行了一次体育模拟测试,把测试结果分为四个等级,即A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘成了如图20-3-1所示的统计图,由此估计全区八年级体育测试成绩达到优秀的人数为________.
图20-3-1
11.某校为了更好地开展“学校特色体育教育”,从全校八年级各班随机抽取了60名学生进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据得到的关于每个个体的测试成绩的部分统计表:
某校60名学生体育测试成绩频数分布表
成绩
划记
频数
百分比
优秀
正正正
a
0.3
良好
正正正正正正
30
b
合格
正
9
0.15
不合格
c
d
合计
(说明:40~55分为不合格,55~70分为合格,70~85分为良好,85~100分为优秀,各分组包括最大值,不包括最小值)
请根据以上信息,解答下列问题:
(1)填空:a=________,b=________,c=________,d=________;
(2)请根据频数分布表,画出相应的频数分布直方图;
(3)这一组数据的中位数落在__________组.
A.40~55分
B.55~70分
C.70~85分
D.85~100分
12.国家规定体质健康状况分为优秀、良好、合格和不合格四种等级.为了了解某地区10000名初中学生的体质健康状况,某校数学兴趣小组从该地区七、八、九年级随机抽取了共500名学生的数据进行整理分析,他们对其中体质健康为优秀的人数做了如图20-3-2所示的分析.
(1)本次随机抽取的七年级人数m=________;
(2)补全条形统计图;
(3)根据抽样调查的结果,估计该地区10000名初中生体质健康状况为优秀的人数.
图20-3-2
13.《中学生体质健康标准》规定学生体质健康等级标准如下:86分及以上为优秀;76分~85分(包括端点值)为良好;60分~75分(包括端点值)为及格;59分及以下为不及格.某校从八年级学生中随机抽取了10%的学生进行了体质测试,得分情况如图20-3-3.
图20-3-3
(1)在抽取的学生中不及格人数所占的百分比是________;
(2)若抽取的学生中优秀的有9人,请算出共抽取了多少名学生;
(3)小明按以下方法计算出抽取的学生的平均分是(90+78+66+42)÷4=69(分).根据你所学的统计知识判断小明的计算是否正确,若不正确,请写出正确的算式(不必算出结果).
14.某班级选派甲、乙两名同学参加学校的跳远比赛,体育老师对他们的5次训练成绩进行了整理,并绘制了以下不完整的统计图表.
甲、乙两人跳远成绩统计表
第1次
第2次
第3次
第4次
第5次
甲成绩(cm)
588
597
608
610
597
乙成绩(cm)
613
618
580
a
618
图20-3-4
根据以上信息,请解答下列问题:
(1)a=________;
(2)请完成图中表示甲成绩变化情况的折线;
(3)通过计算,补全下面的统计分析表:
最好的成绩(cm)
平均数(cm)
众数(cm)
方差
甲
597
65.2
乙
618
600.6
378.24
(4)请依据(3)中所统计的数据,分析甲、乙两名同学的训练成绩各有什么特点.
典题讲评与答案详析
1.【答案】B
【解析】由于总共有9个人,且他们的分数互不相同,第5的成绩是中位数,要判断是否进入前5名,故应知道中位数的多少.
故选:B.
2.【答案】A
【解析】因为有二十二位同学参加,选十一位同学进入下一轮比赛,那么分数从高到低排列后,第11名和第12名的平均的分数就是中位数,所以小明知道自己的分数和中位数后,才能判断自己能否进入下一轮比赛.
故选A.
3.C
解析
由题图,得m=40-5-11-4=20,则该校学生一周课外阅读时间不少于4h的人数占全校人数的百分数约为(20+4)÷4×100%=60%.故选C.
4.B.
5.B.
6.240
解析
先求出样本数据中每周课外阅读时间在1~2(不含1)小时的学生人数的频率,然后再用此频率估算该校每周课外阅读时间在1~2(不含1)小时的学生数即可.
该校每周课外阅读时间在1~2(不含1)小时的学生有1200×=1200×=240(人).
7.8.
8.18.
9.>,乙.
10.360 [解析]
九年级体育测试成绩可以达到优秀的人数约为3600×(1-30%-35%-25%)=360.
11.解:(1)18 0.5 3 0.05
(2)频数分布直方图如图所示.
(3)C
12.解:(1)本次随机抽取的七年级人数m=38÷19%=200.故答案为200.
(2)本次随机抽取的八年级人数为26÷26%=100,
则本次随机抽取的九年级人数为500-200-100=200,
则九年级体质健康为优秀的人数为200×28%=56.
补全条形统计图如图.
某地区七、八、九年级随机抽取学生体质
健康优秀人数的条形统计图
(3)×10000=2400(人).
答:估计该地区10000名初中生体质健康状况为优秀的人数是2400人.
13.解:(1)不及格人数所占的百分比是1-52%-18%-26%=4%.
故答案为4%.
(2)9÷18%=50(名).
答:共抽取了50名学生.
(3)不正确.
正确的算式:
90×18%+78×26%+66×52%+42×4%.
14.解:(1)由折线统计图可知,a=574.
(2)如图所示.
(3)填表如下:
最好的成
绩(cm)
平均数
(cm)
众数(cm)
方差
甲
610
600
597
65.2
乙
618
600.6
618
378.24
(4)从最好的成绩、平均数、众数的角度来看,乙的训练成绩优于甲的训练成绩;
从方差的角度来看,甲的方差小,说明甲的训练成绩比乙的训练成绩稳定.
