8.1基本立体图形-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案)
文档属性
| 名称 | 8.1基本立体图形-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案) |
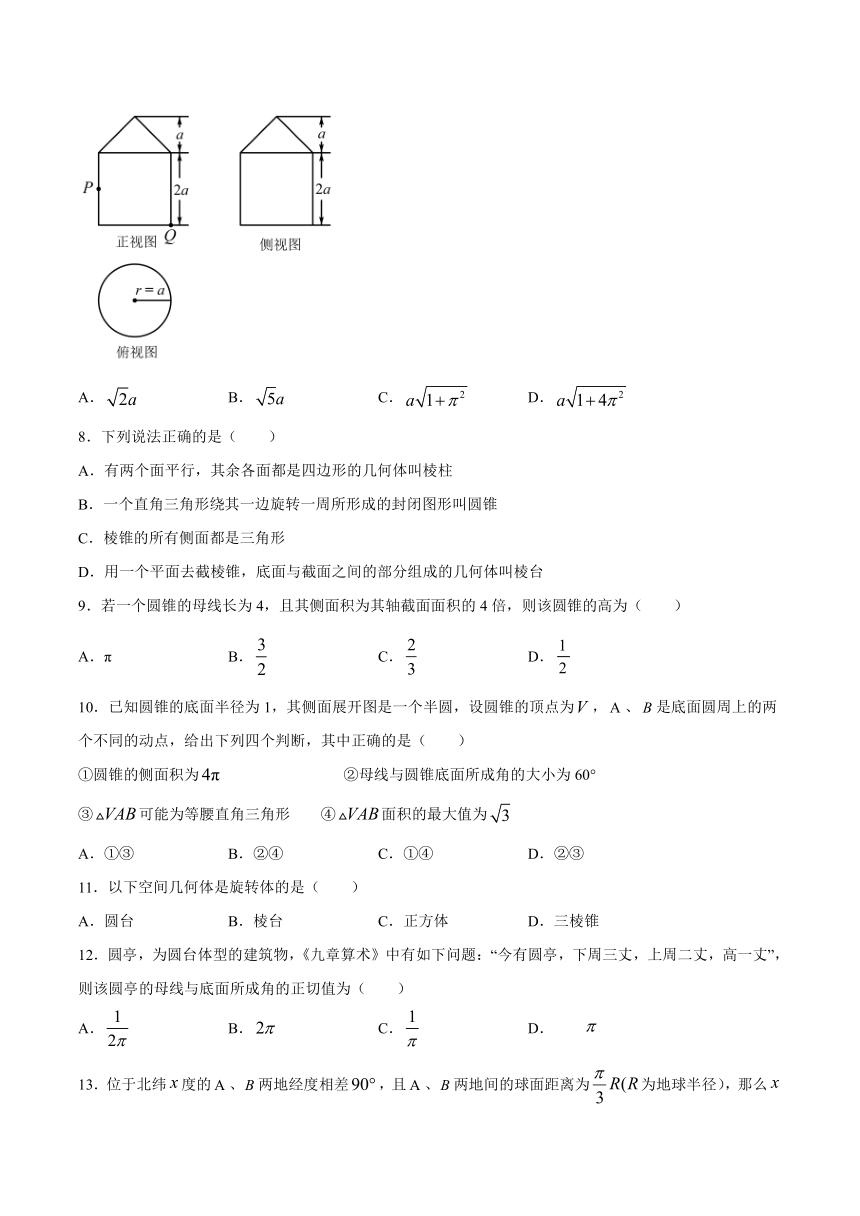
|
|
| 格式 | docx | ||
| 文件大小 | 543.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-21 19:44:17 | ||
图片预览

文档简介
8.1基本立体图形
一、单选题
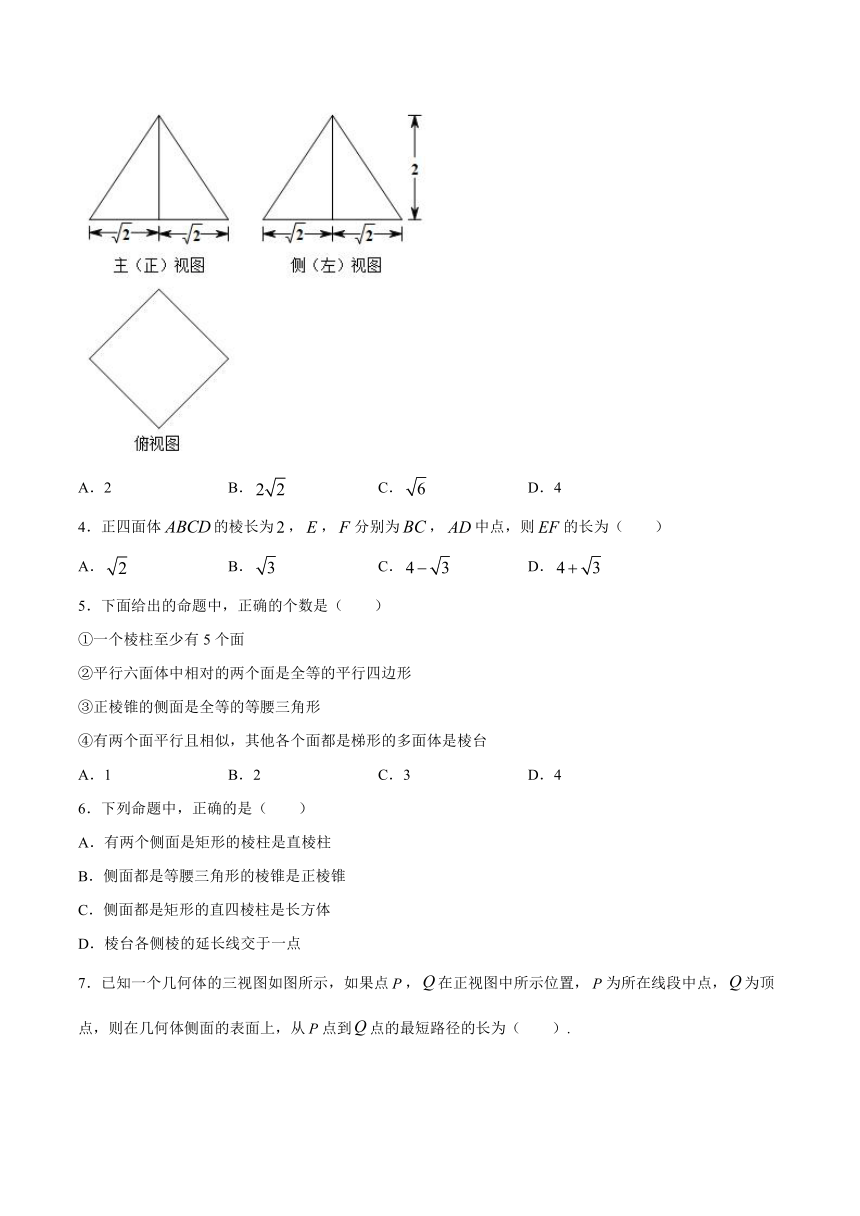
1.如图,在长方体中,,,若面对角线上存在一点,使得取得最小值,则此最小值为(
)
A.
B.
C.
D.
2.如图,长方体被两平面分成三部分,其中,则这三个几何体中是棱柱的个数为(
)
A.0
B.1
C.2
D.3
3.某四棱锥的三视图如图所示,该四棱锥的最长棱的长度为(
)
A.2
B.
C.
D.4
4.正四面体的棱长为,,分别为,中点,则的长为(
)
A.
B.
C.
D.
5.下面给出的命题中,正确的个数是(
)
①一个棱柱至少有5个面
②平行六面体中相对的两个面是全等的平行四边形
③正棱锥的侧面是全等的等腰三角形
④有两个面平行且相似,其他各个面都是梯形的多面体是棱台
A.1
B.2
C.3
D.4
6.下列命题中,正确的是(
)
A.有两个侧面是矩形的棱柱是直棱柱
B.侧面都是等腰三角形的棱锥是正棱锥
C.侧面都是矩形的直四棱柱是长方体
D.棱台各侧棱的延长线交于一点
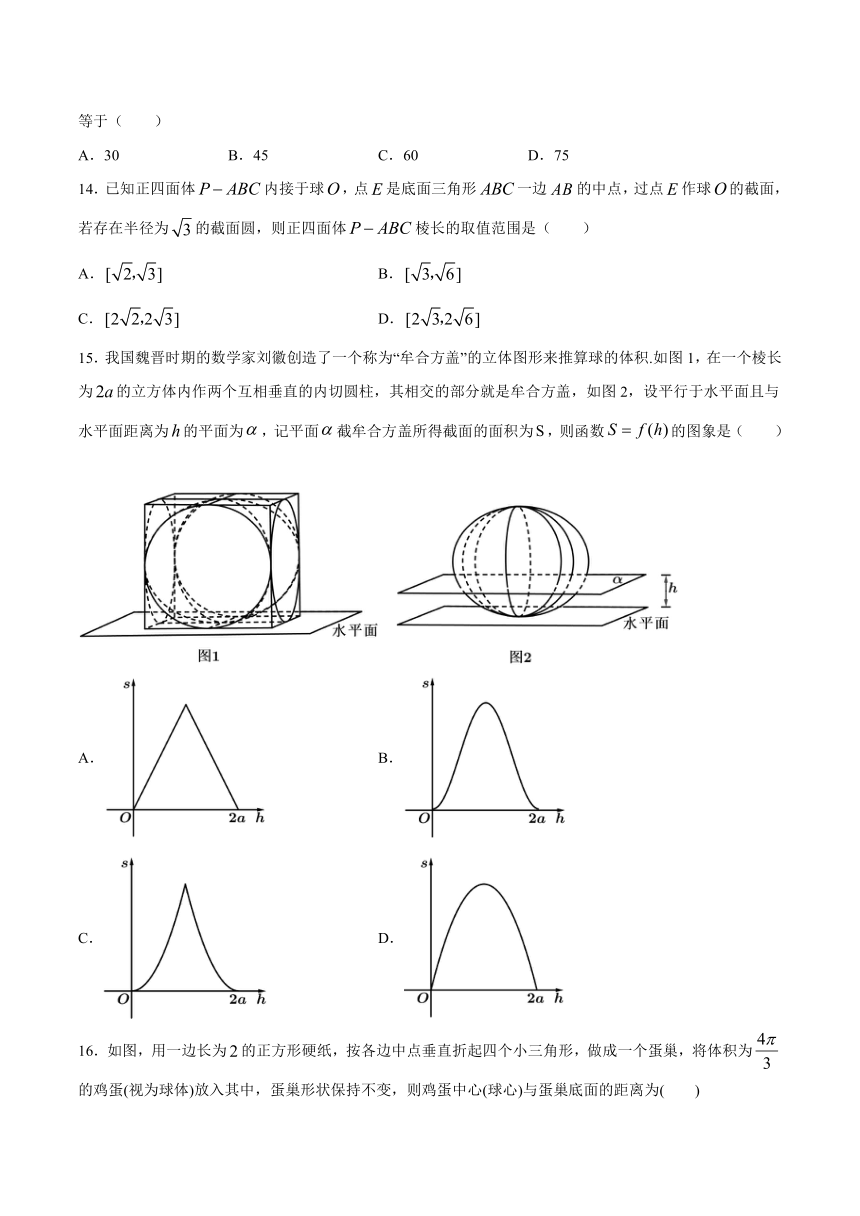
7.已知一个几何体的三视图如图所示,如果点,在正视图中所示位置,为所在线段中点,为顶点,则在几何体侧面的表面上,从点到点的最短路径的长为(
).
A.
B.
C.
D.
8.下列说法正确的是(
)
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.一个直角三角形绕其一边旋转一周所形成的封闭图形叫圆锥
C.棱锥的所有侧面都是三角形
D.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台
9.若一个圆锥的母线长为4,且其侧面积为其轴截面面积的4倍,则该圆锥的高为(
)
A.π
B.
C.
D.
10.已知圆锥的底面半径为1,其侧面展开图是一个半圆,设圆锥的顶点为,、是底面圆周上的两个不同的动点,给出下列四个判断,其中正确的是(
)
①圆锥的侧面积为
②母线与圆锥底面所成角的大小为60°
③可能为等腰直角三角形
④面积的最大值为
A.①③
B.②④
C.①④
D.②③
11.以下空间几何体是旋转体的是(
)
A.圆台
B.棱台
C.正方体
D.三棱锥
12.圆亭,为圆台体型的建筑物,《九章算术》中有如下问题:“今有圆亭,下周三丈,上周二丈,高一丈”,则该圆亭的母线与底面所成角的正切值为(
)
A.
B.
C.
D.
13.位于北纬度的、两地经度相差,且、两地间的球面距离为为地球半径),那么等于(
)
A.30
B.45
C.60
D.75
14.已知正四面体内接于球,点是底面三角形一边的中点,过点作球的截面,若存在半径为的截面圆,则正四面体棱长的取值范围是(
)
A.
B.
C.
D.
15.我国魏晋时期的数学家刘徽创造了一个称为“牟合方盖”的立体图形来推算球的体积.如图1,在一个棱长为的立方体内作两个互相垂直的内切圆柱,其相交的部分就是牟合方盖,如图2,设平行于水平面且与水平面距离为的平面为,记平面截牟合方盖所得截面的面积为,则函数的图象是(
)
A.
B.
C.
D.
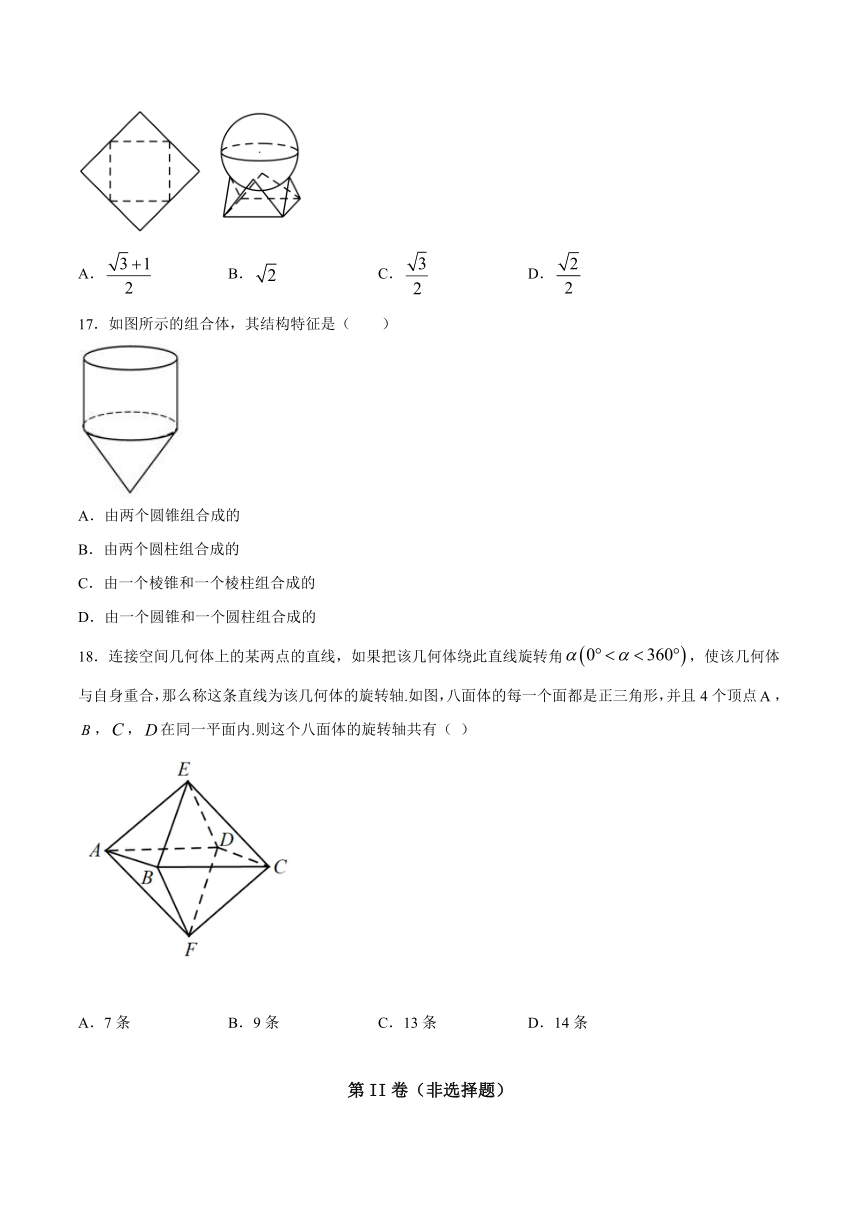
16.如图,用一边长为的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为(
)
A.
B.
C.
D.
17.如图所示的组合体,其结构特征是(
)
A.由两个圆锥组合成的
B.由两个圆柱组合成的
C.由一个棱锥和一个棱柱组合成的
D.由一个圆锥和一个圆柱组合成的
18.连接空间几何体上的某两点的直线,如果把该几何体绕此直线旋转角,使该几何体与自身重合,那么称这条直线为该几何体的旋转轴.如图,八面体的每一个面都是正三角形,并且4个顶点,,,在同一平面内.则这个八面体的旋转轴共有(
)
A.7条
B.9条
C.13条
D.14条
第II卷(非选择题)
请点击修改第II卷的文字说明
二、解答题
19.北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于
与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体在每个顶点有3个面角,每个面角是
,所以正四面体在各顶点的曲率为
,故其总曲率为
.
(1)求四棱锥的总曲率;
(2)若多面体满足:顶点数-棱数+面数
,证明:这类多面体的总曲率是常数.
20.如图所示,长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗?如果是,是几棱柱,并用符号表示;如果不是,请说明理由.
21.如图,圆台的上、下底面半径分别为5cm,10cm,母线长,从圆台母线的中点拉一条绳子绕圆台侧面转到点.求:
(1)绳子的最短长度;
(2)在绳子最短时,求上底面圆周上的点到绳子的最短距离.
参考答案
1.D
2.D
3.C
4.A
5.C
6.D
7.C
8.C
9.A
10.B
11.A
12.B
13.B
14.C
15.D
16.B
17.D
18.C
19.【答案】
(1)解:由题可知:四棱锥的总曲率等于四棱锥各顶点的曲率之和.
可以从整个多面体的角度考虑,所有顶点相关的面角就是多面体的所有多边形表面的内角的集合.由图可知:四棱锥共有5个顶点,5个面,其中4个为三角形,1个为四边形.
所以四棱锥的表面内角和由4个为三角形,1个为四边形组成,
则其总曲率为:
.
(2)证明:设顶点数、棱数、面数分别为
、
、
,所以有
设第
个面的棱数为
,所以
所以总曲率为:
所以这类多面体的总曲率是常数.
【解析】(1)利用规定:多面体顶点的曲率等于
与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和。
由题可知,四棱锥的总曲率等于四棱锥各顶点的曲率之和,可以从整个多面体的角度考虑,所有顶点相关的面角就是多面体的所有多边形表面的内角的集合
。再利用四棱锥的结构特征求出四棱锥的总曲率。
(2)
设顶点数、棱数、面数分别为
、
、
,所以有
,
设第
个面的棱数为
,所以
,
从而结合总曲率的求解方法,从而求出这类多面体的总曲率,进而证出这类多面体的总曲率是常数。
20.(1)是棱柱,并且是四棱柱(2)截面BCNM的右上方部分是三棱柱BB1M-CC1N,左下方部分是四棱柱ABMA1-DCND1.
21.(1)50cm;(2)4cm
一、单选题
1.如图,在长方体中,,,若面对角线上存在一点,使得取得最小值,则此最小值为(
)
A.
B.
C.
D.
2.如图,长方体被两平面分成三部分,其中,则这三个几何体中是棱柱的个数为(
)
A.0
B.1
C.2
D.3
3.某四棱锥的三视图如图所示,该四棱锥的最长棱的长度为(
)
A.2
B.
C.
D.4
4.正四面体的棱长为,,分别为,中点,则的长为(
)
A.
B.
C.
D.
5.下面给出的命题中,正确的个数是(
)
①一个棱柱至少有5个面
②平行六面体中相对的两个面是全等的平行四边形
③正棱锥的侧面是全等的等腰三角形
④有两个面平行且相似,其他各个面都是梯形的多面体是棱台
A.1
B.2
C.3
D.4
6.下列命题中,正确的是(
)
A.有两个侧面是矩形的棱柱是直棱柱
B.侧面都是等腰三角形的棱锥是正棱锥
C.侧面都是矩形的直四棱柱是长方体
D.棱台各侧棱的延长线交于一点
7.已知一个几何体的三视图如图所示,如果点,在正视图中所示位置,为所在线段中点,为顶点,则在几何体侧面的表面上,从点到点的最短路径的长为(
).
A.
B.
C.
D.
8.下列说法正确的是(
)
A.有两个面平行,其余各面都是四边形的几何体叫棱柱
B.一个直角三角形绕其一边旋转一周所形成的封闭图形叫圆锥
C.棱锥的所有侧面都是三角形
D.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台
9.若一个圆锥的母线长为4,且其侧面积为其轴截面面积的4倍,则该圆锥的高为(
)
A.π
B.
C.
D.
10.已知圆锥的底面半径为1,其侧面展开图是一个半圆,设圆锥的顶点为,、是底面圆周上的两个不同的动点,给出下列四个判断,其中正确的是(
)
①圆锥的侧面积为
②母线与圆锥底面所成角的大小为60°
③可能为等腰直角三角形
④面积的最大值为
A.①③
B.②④
C.①④
D.②③
11.以下空间几何体是旋转体的是(
)
A.圆台
B.棱台
C.正方体
D.三棱锥
12.圆亭,为圆台体型的建筑物,《九章算术》中有如下问题:“今有圆亭,下周三丈,上周二丈,高一丈”,则该圆亭的母线与底面所成角的正切值为(
)
A.
B.
C.
D.
13.位于北纬度的、两地经度相差,且、两地间的球面距离为为地球半径),那么等于(
)
A.30
B.45
C.60
D.75
14.已知正四面体内接于球,点是底面三角形一边的中点,过点作球的截面,若存在半径为的截面圆,则正四面体棱长的取值范围是(
)
A.
B.
C.
D.
15.我国魏晋时期的数学家刘徽创造了一个称为“牟合方盖”的立体图形来推算球的体积.如图1,在一个棱长为的立方体内作两个互相垂直的内切圆柱,其相交的部分就是牟合方盖,如图2,设平行于水平面且与水平面距离为的平面为,记平面截牟合方盖所得截面的面积为,则函数的图象是(
)
A.
B.
C.
D.
16.如图,用一边长为的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为(
)
A.
B.
C.
D.
17.如图所示的组合体,其结构特征是(
)
A.由两个圆锥组合成的
B.由两个圆柱组合成的
C.由一个棱锥和一个棱柱组合成的
D.由一个圆锥和一个圆柱组合成的
18.连接空间几何体上的某两点的直线,如果把该几何体绕此直线旋转角,使该几何体与自身重合,那么称这条直线为该几何体的旋转轴.如图,八面体的每一个面都是正三角形,并且4个顶点,,,在同一平面内.则这个八面体的旋转轴共有(
)
A.7条
B.9条
C.13条
D.14条
第II卷(非选择题)
请点击修改第II卷的文字说明
二、解答题
19.北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于
与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体在每个顶点有3个面角,每个面角是
,所以正四面体在各顶点的曲率为
,故其总曲率为
.
(1)求四棱锥的总曲率;
(2)若多面体满足:顶点数-棱数+面数
,证明:这类多面体的总曲率是常数.
20.如图所示,长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗?如果是,是几棱柱,并用符号表示;如果不是,请说明理由.
21.如图,圆台的上、下底面半径分别为5cm,10cm,母线长,从圆台母线的中点拉一条绳子绕圆台侧面转到点.求:
(1)绳子的最短长度;
(2)在绳子最短时,求上底面圆周上的点到绳子的最短距离.
参考答案
1.D
2.D
3.C
4.A
5.C
6.D
7.C
8.C
9.A
10.B
11.A
12.B
13.B
14.C
15.D
16.B
17.D
18.C
19.【答案】
(1)解:由题可知:四棱锥的总曲率等于四棱锥各顶点的曲率之和.
可以从整个多面体的角度考虑,所有顶点相关的面角就是多面体的所有多边形表面的内角的集合.由图可知:四棱锥共有5个顶点,5个面,其中4个为三角形,1个为四边形.
所以四棱锥的表面内角和由4个为三角形,1个为四边形组成,
则其总曲率为:
.
(2)证明:设顶点数、棱数、面数分别为
、
、
,所以有
设第
个面的棱数为
,所以
所以总曲率为:
所以这类多面体的总曲率是常数.
【解析】(1)利用规定:多面体顶点的曲率等于
与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和。
由题可知,四棱锥的总曲率等于四棱锥各顶点的曲率之和,可以从整个多面体的角度考虑,所有顶点相关的面角就是多面体的所有多边形表面的内角的集合
。再利用四棱锥的结构特征求出四棱锥的总曲率。
(2)
设顶点数、棱数、面数分别为
、
、
,所以有
,
设第
个面的棱数为
,所以
,
从而结合总曲率的求解方法,从而求出这类多面体的总曲率,进而证出这类多面体的总曲率是常数。
20.(1)是棱柱,并且是四棱柱(2)截面BCNM的右上方部分是三棱柱BB1M-CC1N,左下方部分是四棱柱ABMA1-DCND1.
21.(1)50cm;(2)4cm
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
