2020-2021学年人教版七年级下册第九章不等式与不等式组含参数专项复习课件(25张)
文档属性
| 名称 | 2020-2021学年人教版七年级下册第九章不等式与不等式组含参数专项复习课件(25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 583.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-20 11:30:48 | ||
图片预览








文档简介
不等式(组)含参数专项
类型一、给出确定整数解求参数
例1.如果关于x的不等式组 的整数解仅为1,2,3,
那么适合这个不等式组的整数对(m,n)共有( )
A.49对 B.42对 C.36对 D.13对
类型一、给出确定整数解求参数:
例1.如果关于x的不等式组 的整数解仅为1,2,3,
那么适合这个不等式组的整数对(m,n)共有( )
A.49对 B.42对 C.36对 D.13对
分析:
①解x取值范围;
②求出m,n的取值;
③确定整数对(m,n)。
类型一、给出确定整数解求参数:
例1.如果关于x的不等式组 的整数解仅为1,2,3,那么适合这个不等式组的整数对(m,n)共有( )
A.49对 B.42对 C.36对 D.13对
类型一、给出确定整数解求参数:
解:??????????≥????7
x?
0 1 2 3 4 5
∴?????0<????7<1 3<????6<4
?
设 ????7=0,则:0≤x< ????6?
设?????7=1,则:1≤x< ????6
?
设 ????6=3,则: ????7?≤x<3
设 ????6=4,则: ????7?≤x<4
?
∴?????0<????7≤1 ???3<????6≤4
?
m:1,2,3,4,
5,6,7
n: 19,20,21,
22,23,24,
(m,n)整数对共有:
7×6=42对
∴ ????7≤x<????6
?
×
√
×
√
?????7 ????6
?
18<n≤24
0<m≤7
归纳总结:
①解不等式组;
②数形结合,画数轴分析;
③验证端点的取舍;
④求解参数。
易错点:临界点是否能取等号!!!
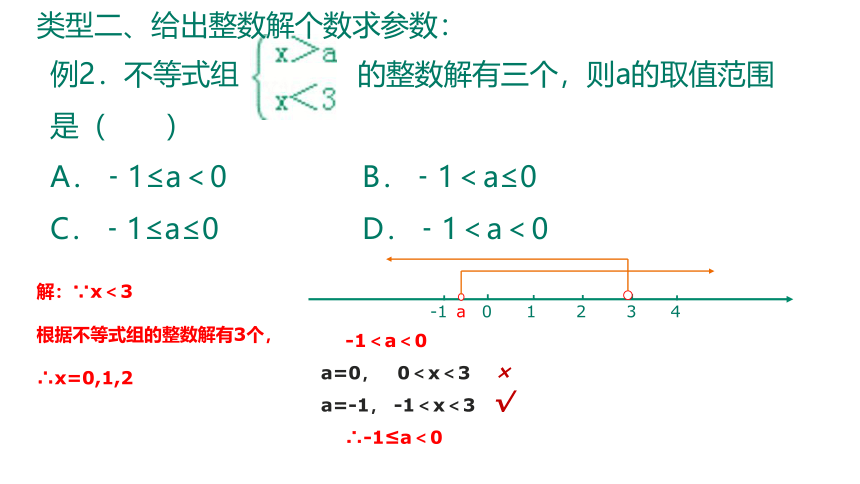
类型二、给出整数解个数求参数
例2.不等式组 的整数解有三个,则a的取值范围是( )
A.﹣1≤a<0 B.﹣1<a≤0
C.﹣1≤a≤0 D.﹣1<a<0
类型二、给出整数解个数求参数:
-1 0 1 2 3 4
解:∵x<3
根据不等式组的整数解有3个,
∴x=0,1,2
-1<a<0
a=0, 0<x<3
a=-1, -1<x<3
∴-1≤a<0
×
√
a
例3.若关于x的不等式组 只有4个整数解, 求a的取值范围.
&????+????????????>?????????&????????+?????????
分析:
①解不等式组,
②从解集中找出适合条件的整数解,
③确定字母的取值范围。
类型二、给出整数解个数求参数:
例3.若关于x的不等式组 只有4个整数解,求a的取值范围.
&????+????????????>?????????&????????+?????????
类型二、给出整数解个数求参数:
解:
????+????????????>?????????
x+15>2x-6
x<21
?
????????+???????? 2x+2<3x+3a
x>2-3a
?
∴ 2-3a<x<21
根据不等式组只有4个整数解
∴x=20,19,18,17
16 17 18 19 20 21
16<2-3a<17
2-3a=16时,不等式组解集:16<x<21
2-3a=17时,不等式组解集:17<x<21
∴ 16≤2-3a<17
14≤-3a<15
-143≥a>-5
∴-5<a≤ -143
?
2-3a
√
×
不等式组整数解的取值问题,一般可按以下几个步骤解题:
①求出不等式组的解集(用含参数的代数式来表示);
②画数轴,初步确定范围(两个临界点必为相邻的整数);
③判断两个临界点中,哪一个可取等于号;
④确定参数的取值范围。
类型三、有解无解问题
不等式组解的情况:
a
b
a
b
a
b
a
b
(1)同大取大
(2)同小取小
(3)大小,小大取中间
(4)大大,小小是无解
x>b
x<a
a<x<b
无解
a≠b
不等式组无解
1.若关于x的不等式组 无解, 则a的取值范围是_____
分析:利用大大小小是无解,并且考虑相等的情况。
x<3a+2
x>a-4
a≤-3
a-4>3a+2
a-4≥3a+2
a-3a≥6
-2a≥6
a≤-3
x<2
x>2
无解
不等式组有解
2.若关于x的不等式组 有解, 则k的取值范围是_____
x+3>0
-2k-x+6>0
分析:先求解,利用大小,小大取中间,进行分析。
x>-3
x<-2k+6
-
-3<-2k+6
k<
9
2
_
2k<9
不等式组解的情况:
a
b
a
b
a
b
a
b
(1)同大取大
(2)同小取小
(3)大小,小大取中间
(4)大大,小小是无解
例1.已知不等式组 有解但没有整数解, 则k的取值范围是_____
不等式组有解但无整数解
x+3>0
-2k-x+6>0
-3
-2
m
-3<-2k+6
x>-3
x<-2k+6
≤-2
-9<-2k≤-8
4≤ k<
9
2
_
分析:先求解,有解判断,确定在哪两个整数之间,等号是否成立。
类型四、解的范围问题
一、解不等式组的步骤:
(1)解各不等式:求出各个一元一次不等式的解集,并在同一数轴上表示;
(2)确定不等式组解集:若有公共部分,则用不等式表示出来即为不等式组的解集;若无公共部分,则不等式组无解.
解不等式①,得
解不等式②,得
(2)确定不等式组解集
{69012ECD-51FC-41F1-AA8D-1B2483CD663E}不 等 式 组
数 轴 表 示 ( a解 集
口 诀
①
同大取大
②
同小取小
③
大小,小大取中间
④
无解
大大,小小是无解
a
b
a
b
a
b
a
b
【例1】
若关于 x 的不等式组 的解集是 x>2,则 a 的取值范围是_________ .
②根据口诀确定参数大致范围
③端点值单独确定能否可取
a ≤ 2
x>2
x>a
∴ a<2
a=2
x>2
x>2
由题意得
∴ a≤2
解:
或
①带着参数解不等式组
同大取大
利用已知解集求参数的步骤:
(1)带着参数解不等式组;
(2)根据口诀确定参数大致范围;
(3)端点值单独确定能否可取 .
【例2】
若关于 x 的不等式组 的解集是 2①带着参数解不等式组
②双侧解集直接对应端点值
【例3】
若关于 x 的不等式组 的解集是 3<x<a+2,则 a 的取值范围是_________ .
①重新组合出同向的两个不等式组
②转化为例1单侧解法
③端点值单独确定能否可取
④左端点小于右端点
感谢聆听
类型一、给出确定整数解求参数
例1.如果关于x的不等式组 的整数解仅为1,2,3,
那么适合这个不等式组的整数对(m,n)共有( )
A.49对 B.42对 C.36对 D.13对
类型一、给出确定整数解求参数:
例1.如果关于x的不等式组 的整数解仅为1,2,3,
那么适合这个不等式组的整数对(m,n)共有( )
A.49对 B.42对 C.36对 D.13对
分析:
①解x取值范围;
②求出m,n的取值;
③确定整数对(m,n)。
类型一、给出确定整数解求参数:
例1.如果关于x的不等式组 的整数解仅为1,2,3,那么适合这个不等式组的整数对(m,n)共有( )
A.49对 B.42对 C.36对 D.13对
类型一、给出确定整数解求参数:
解:??????????≥????7
x?
0 1 2 3 4 5
∴?????0<????7<1 3<????6<4
?
设 ????7=0,则:0≤x< ????6?
设?????7=1,则:1≤x< ????6
?
设 ????6=3,则: ????7?≤x<3
设 ????6=4,则: ????7?≤x<4
?
∴?????0<????7≤1 ???3<????6≤4
?
m:1,2,3,4,
5,6,7
n: 19,20,21,
22,23,24,
(m,n)整数对共有:
7×6=42对
∴ ????7≤x<????6
?
×
√
×
√
?????7 ????6
?
18<n≤24
0<m≤7
归纳总结:
①解不等式组;
②数形结合,画数轴分析;
③验证端点的取舍;
④求解参数。
易错点:临界点是否能取等号!!!
类型二、给出整数解个数求参数
例2.不等式组 的整数解有三个,则a的取值范围是( )
A.﹣1≤a<0 B.﹣1<a≤0
C.﹣1≤a≤0 D.﹣1<a<0
类型二、给出整数解个数求参数:
-1 0 1 2 3 4
解:∵x<3
根据不等式组的整数解有3个,
∴x=0,1,2
-1<a<0
a=0, 0<x<3
a=-1, -1<x<3
∴-1≤a<0
×
√
a
例3.若关于x的不等式组 只有4个整数解, 求a的取值范围.
&????+????????????>?????????&????????+?????????
分析:
①解不等式组,
②从解集中找出适合条件的整数解,
③确定字母的取值范围。
类型二、给出整数解个数求参数:
例3.若关于x的不等式组 只有4个整数解,求a的取值范围.
&????+????????????>?????????&????????+?????????
类型二、给出整数解个数求参数:
解:
????+????????????>?????????
x+15>2x-6
x<21
?
????????+???????? 2x+2<3x+3a
x>2-3a
?
∴ 2-3a<x<21
根据不等式组只有4个整数解
∴x=20,19,18,17
16 17 18 19 20 21
16<2-3a<17
2-3a=16时,不等式组解集:16<x<21
2-3a=17时,不等式组解集:17<x<21
∴ 16≤2-3a<17
14≤-3a<15
-143≥a>-5
∴-5<a≤ -143
?
2-3a
√
×
不等式组整数解的取值问题,一般可按以下几个步骤解题:
①求出不等式组的解集(用含参数的代数式来表示);
②画数轴,初步确定范围(两个临界点必为相邻的整数);
③判断两个临界点中,哪一个可取等于号;
④确定参数的取值范围。
类型三、有解无解问题
不等式组解的情况:
a
b
a
b
a
b
a
b
(1)同大取大
(2)同小取小
(3)大小,小大取中间
(4)大大,小小是无解
x>b
x<a
a<x<b
无解
a≠b
不等式组无解
1.若关于x的不等式组 无解, 则a的取值范围是_____
分析:利用大大小小是无解,并且考虑相等的情况。
x<3a+2
x>a-4
a≤-3
a-4>3a+2
a-4≥3a+2
a-3a≥6
-2a≥6
a≤-3
x<2
x>2
无解
不等式组有解
2.若关于x的不等式组 有解, 则k的取值范围是_____
x+3>0
-2k-x+6>0
分析:先求解,利用大小,小大取中间,进行分析。
x>-3
x<-2k+6
-
-3<-2k+6
k<
9
2
_
2k<9
不等式组解的情况:
a
b
a
b
a
b
a
b
(1)同大取大
(2)同小取小
(3)大小,小大取中间
(4)大大,小小是无解
例1.已知不等式组 有解但没有整数解, 则k的取值范围是_____
不等式组有解但无整数解
x+3>0
-2k-x+6>0
-3
-2
m
-3<-2k+6
x>-3
x<-2k+6
≤-2
-9<-2k≤-8
4≤ k<
9
2
_
分析:先求解,有解判断,确定在哪两个整数之间,等号是否成立。
类型四、解的范围问题
一、解不等式组的步骤:
(1)解各不等式:求出各个一元一次不等式的解集,并在同一数轴上表示;
(2)确定不等式组解集:若有公共部分,则用不等式表示出来即为不等式组的解集;若无公共部分,则不等式组无解.
解不等式①,得
解不等式②,得
(2)确定不等式组解集
{69012ECD-51FC-41F1-AA8D-1B2483CD663E}不 等 式 组
数 轴 表 示 ( a解 集
口 诀
①
同大取大
②
同小取小
③
大小,小大取中间
④
无解
大大,小小是无解
a
b
a
b
a
b
a
b
【例1】
若关于 x 的不等式组 的解集是 x>2,则 a 的取值范围是_________ .
②根据口诀确定参数大致范围
③端点值单独确定能否可取
a ≤ 2
x>2
x>a
∴ a<2
a=2
x>2
x>2
由题意得
∴ a≤2
解:
或
①带着参数解不等式组
同大取大
利用已知解集求参数的步骤:
(1)带着参数解不等式组;
(2)根据口诀确定参数大致范围;
(3)端点值单独确定能否可取 .
【例2】
若关于 x 的不等式组 的解集是 2
②双侧解集直接对应端点值
【例3】
若关于 x 的不等式组 的解集是 3<x<a+2,则 a 的取值范围是_________ .
①重新组合出同向的两个不等式组
②转化为例1单侧解法
③端点值单独确定能否可取
④左端点小于右端点
感谢聆听
