2020-2021学年八年级数学湘教版下册第3章图形与坐标 期末综合优生辅导训练(word版含解析)
文档属性
| 名称 | 2020-2021学年八年级数学湘教版下册第3章图形与坐标 期末综合优生辅导训练(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 457.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-22 10:15:51 | ||
图片预览




文档简介
2021年湘教版八年级数学下册《第3章图形与坐标》期末综合优生辅导训练(附答案)
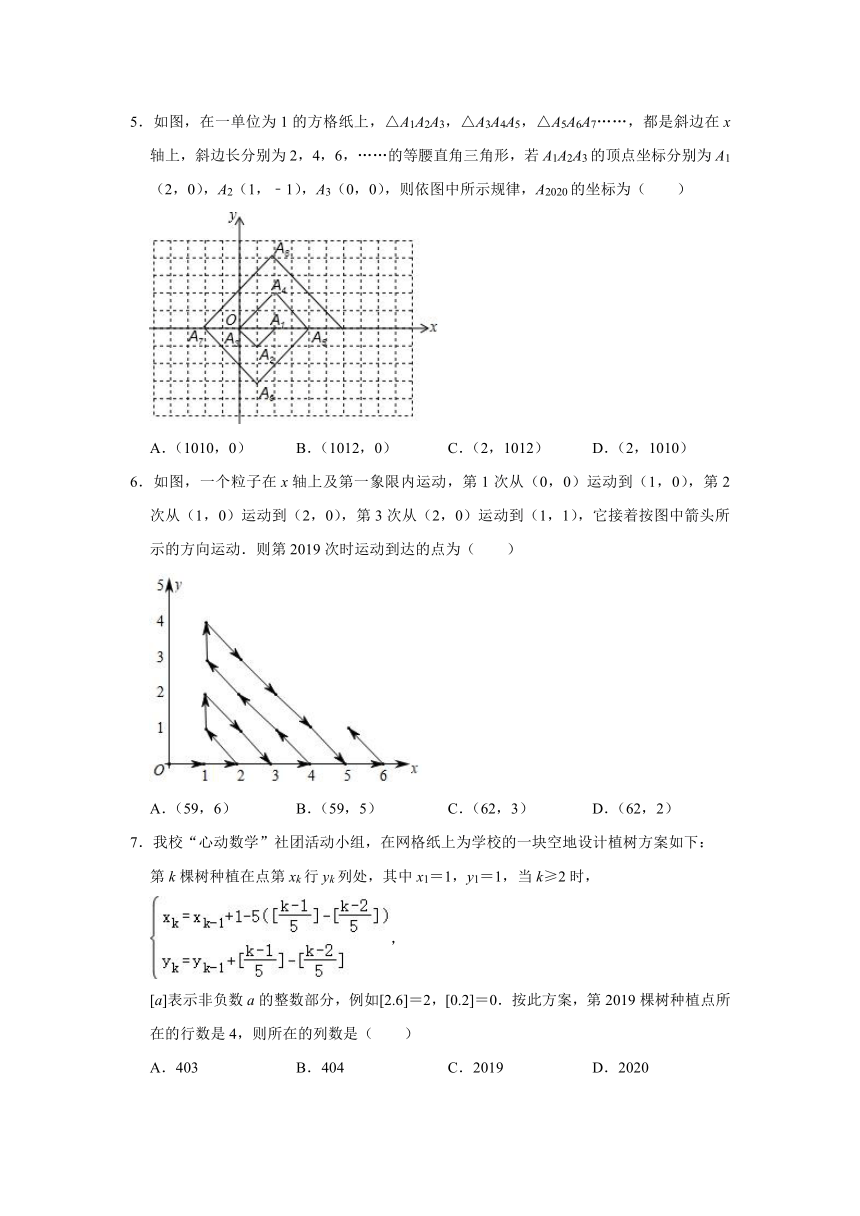
1.如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(﹣2,2),第四次向右跳动5个单位至点A4(3,2),…,以此规律跳动下去,点A第2020次跳动至点A2020的坐标是( )
A.(1012,1011) B.(1009,1008)
C.(1010,1009) D.(1011,1010)
2.在平面直角坐标系中,点M在第四象限,到x轴,y轴的距离分别为6,4,则点M的坐标为( )
A.(4,﹣6) B.(﹣4,6) C.(﹣6,4) D.(﹣6,﹣4)
3.已知m为任意实数,则点A(m,m2+1)不在( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限
4. 一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动,且每秒移动一个单位,那么第2020秒时质点所在位置的坐标是( )
A.(4,16) B.(44,44) C.(44,4) D.(4,44)
5.如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7……,都是斜边在x轴上,斜边长分别为2,4,6,……的等腰直角三角形,若A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2020的坐标为( )
A.(1010,0) B.(1012,0) C.(2,1012) D.(2,1010)
6.如图,一个粒子在x轴上及第一象限内运动,第1次从(0,0)运动到(1,0),第2次从(1,0)运动到(2,0),第3次从(2,0)运动到(1,1),它接着按图中箭头所示的方向运动.则第2019次时运动到达的点为( )
A.(59,6) B.(59,5) C.(62,3) D.(62,2)
7.我校“心动数学”社团活动小组,在网格纸上为学校的一块空地设计植树方案如下:
第k棵树种植在点第xk行yk列处,其中x1=1,y1=1,当k≥2时,
,
[a]表示非负数a的整数部分,例如[2.6]=2,[0.2]=0.按此方案,第2019棵树种植点所在的行数是4,则所在的列数是( )
A.403 B.404 C.2019 D.2020
8.在平面直角坐标系中,点P与点M关于y轴对称,点N与点M关于x轴对称,若点P的坐标为(﹣2,3),则点N的坐标为( )
A.(﹣3,2) B.(2,3) C.(2,﹣3) D.(﹣2,﹣3)
9.已知M(2,2).规定“把点M先作关于x轴对称,再向左平移1个单位”为一次变换.那么连续经过2020次变换后,点M的坐标变为( )
A.(﹣2018,2) B.(﹣2018,﹣2) C.(﹣2019,﹣2) D.(﹣2019,2)
10.已知坐标平面内的点A(﹣2,4),如果将平面直角坐标系向左平移3个单位长度,再向上平移2个单位长度,那么平移后点A的坐标是( )
A.(1,6) B.(﹣5,6) C.(﹣5,2) D.(1,2)
11.线段AB经过平移得到线段CD,其中点A、B的对应点分别为点C、D,这四个点都在如图所示的格点上,那么线段AB上的一点P(a,b)经过平移后,在线段CD上的对应点Q的坐标是( )
A.(a﹣1,b+3) B.(a﹣1,b﹣3) C.(a+1,b+3) D.(a+1,b﹣3)
12.如图,在平面直角坐标系中有一个2×2的正方形网格,每个格点的横、纵坐标均为整数,已知点A(1,2),作直线OA并向右平移k个单位,要使分布在平移后的直线两侧的格点数相同,则k的值为( )
A. B. C. D.1
13.已知点A关于x轴的对称点坐标为(﹣1,2),则点A关于原点的对称点的坐标为( )
A.(1,2) B.(﹣1,﹣2) C.(2,﹣1) D.(1,﹣2)
14.在平面直角坐标系中有三个点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点P2,P2关于C的对称点为P3,按此规律继续以A、B、C为对称中心重复前面的操作,依次得到P4,P5,P6,…,则点P2018的坐标是( )
A.(0,0) B.(0,2) C.(2,﹣4) D.(﹣4,2)
15.在平面直角坐标系xOy中,将等腰直角三角形AOB按如图所示的位置放置,然后绕原点O逆时针旋转90°到△A'OB'的位置,若点B的坐标为B(4,0),则点A'的坐标为( )
A.(2,2) B.(2,2) C.(﹣2,2) D.(﹣2,2)
16.如图,在平面直角坐标系内,点A、点B的坐标分别为A(﹣7,0),B(5,0),现将线段AB向上平移9个单位,得到对应线段DC,连接AD、BC、AC,若AC=15,动点E从C点出发,以每秒3个单位的速度沿C→D→C作匀速移动,点F从点B出发,以每秒4个单位的速度沿B→A→B作匀速运动,点G从点A出发沿AC向点C匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.在移动过程中,若△CEG与△AFG全等,则此时的移动时间t的值为 .
17.如图,等边三角形ABO的边长为2,O为坐标原点,A在x轴上,B在第二象限.△ABO沿x轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是 ;翻滚2018次后AB中点M的纵坐标为 .
18.已知(a﹣2)2+|b+3|=0,则点P(﹣a,﹣b)在第 象限.
19.如图,在平面直角坐标系xOy中,点A(3,0),判断在M,N,P,Q四点中,满足到点O和点A的距离都小于2的点是 .
20.在平面直角坐标系中,将点(﹣b,﹣a)称为点(a,b)的“关联点”(例如点(﹣2,﹣1)是点(1,2)的“关联点”).如果一个点和它的“关联点”在同一象限内,那么这一点在第 象限.
21.如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2021秒时,点P的坐标是 .
22.在直角坐标系中,下面各点按顺序依次排列:(1,0),(0,1),(1,1),(﹣2,0),(0,﹣2),(﹣2,﹣2),(3,0),(0,3),(3,3),(﹣4,0),(0,﹣4),(﹣4,﹣4)…,按此规律,这列点中第1000个点的坐标是 .
23.如图,在平面直角坐标系中,已知正方形ABCD的边长为8,与y轴交于点M(0,5),顶点C(6,﹣3),将一条长为2020个单位长度且没有弹性的细绳一端固定在点M处,从点M出发将细绳紧绕在正方形ABCD的边上,则细绳的另一端到达的位置点N的坐标为 .
24.教材上曾让同学们探索过线段的中点坐标:在平面直角坐标系中,若两点A(x1,y1)、B(x2,y2),所连线段AB的中点是M,则M的坐标为(,),例如:点A(1,2)、点B(3,6),则线段AB的中点M的坐标为(,),即M(2,4)请利用以上结论解决问题:在平面直角坐标系中,若点E(a﹣1,a),F(b,a﹣b),线段EF的中点G恰好位于x轴上,且到y轴的距离是2,则2a+b的值等于 .
25.已知A(1,2)、B(﹣3,1),点P在y轴上,则当y轴平分∠APB时,点P的坐标为 .
26.已知AB∥x轴,点A的坐标为(2,5),并且AB=4,则点B的坐标为 .
27.在平面直角坐标系中,点A(a,﹣3)向左平移3个单位得点A′,若点A和A′关于y轴对称,则a= .
28.若P关于x轴的对称点为(3,a),关于y轴对称的点为(b,2),则P点的坐标为 .
29.已知△ABO关于x轴对称,点A的坐标为(1,﹣2),若在坐标轴上有一个点P,满足△BOP的面积等于2,则点P的坐标为 .
30.如图,在平面直角坐标系中,已知点A的坐标为(4,4),若△ABC是关于直线y=1的轴对称图形,则点B的坐标为 ;若△ABC是关于直线y=a的轴对称图形,则点B的坐标为 .
31.如图,在直角坐标系中,设一动点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,…则x1+x2+…+x99+x100= .
32.我们规定:若点O是线段MN的中点,则称点M关于O的对称点是N(或称点M与点N关于O成中心对称);若直线n是线段MN的垂直平分线,则称点M关于n的对称点是N(或称点M与点N关于n成轴对称),如图现有石头A和石头B关于竹竿l对称,石头A和石头B相距80cm一只电子青蛙位于点P,与石头A相距60cm,与竹竿l相距30cm,他按照如下指令跳动:第一跳落点于P1,P与P1关于点A成中心对称;第二跳落点于P2,P2与P1关于竹竿l成轴对称;第三跳落点于P3,P3与P2关于点B成中心对称;第四跳落点于P4,P4与P3关于竹竿l成轴对称;以此跃下去,若每25跳可以休息一次.
(1)画出这只电子青蛙前四跳运动的路线图,并求点P4与点P1的距离(不须说明理由)
(2)求电子青蛙第三次休息点与点P的距离.
33.如图:在直角坐标系中,第一次将△AOB变换成△OA1B1,第二次将三角形变换成△OA2B2,第三次将△OA2B2,变换成△OA3B3,已知A(1,3),A1(3,3),A2(5,3),A3(7,3);B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此变化规律再将△OA3B3变换成△OA4B4,则A4的坐标是 ,B4的坐标是 .
(2)若按(1)找到的规律将△OAB进行了n次变换,得到△OAnBn,比较每次变换中三角形顶点有何变化,找出规律,推测An的坐标是 ,Bn的坐标是 .
34.小明在研究苏教版《有趣的坐标系》后,得到启发,针对正六边形OABCDE,自己设计了一个坐标系如图,该坐标系以O为原点,直线OA为x轴,直线OE为y轴,以正六边形OABCDE的边长为一个单位长.坐标系中的任意一点P用一有序实数对(a,b)来表示,我们称这个有序实数对(a,b)为点P的坐标.坐标系中点的坐标的确定方法如下:
(ⅰ)x轴上点M的坐标为(m,0),其中m为M点在x轴上表示的实数;
(ⅱ)y轴上点N的坐标为(0,n),其中n为N点在y轴上表示的实数;
(ⅲ)不在x、y轴上的点Q的坐标为(a,b),其中a为过点Q且与y轴平行的直线与x轴的交点在x轴上表示的实数,b为过点Q且与x轴平行的直线与y轴的交点在y轴上表示的实数.
则:(1)分别写出点A、B、C的坐标;
(2)标出点M(2,3)的位置;
(3)若点K(x,y)为射线OD上任一点,求x与y所满足的关系式.
35.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
36.先阅读下列一段文字,再解答问题
已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|
(1)已知点A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点间的距离;
(3)已知点A(0,6)B(﹣3,2),C(3,2),判断线段AB,BC,AC中哪两条是相等的?并说明理由.
37.在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,0)、B(5,0)、C(3,3),D(2,4).
(1)求:四边形ABCD的面积.
(2)如果把四边形ABCD先向左平移3个单位,再向下平移1个单位得四边形A′B′C′D',求A',B′,C',D′点坐标.
38.已知在平面直角坐标系中,A(﹣a,a),a≠0,B(b,c),a、b、c满足a﹣2b﹣3c=﹣1,2a﹣3b﹣5c=﹣4.
(1)若c=0,求A、B两点的坐标;
(2)在(1)的条件下,C(m,0)为一动点,且m>0,连接AB、AC,平移线段AB得到线段ED,使B点的对应点D落在线段AC上,则∠EDC、∠ABC、∠ACB之间有何数量关系?证明你的结论;
(3)若将线段AB平移到OF处,点F在第二象限,坐标原点O与点A对应,F与B对应,求F点的坐标.
39.已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值;
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
40.(1)点P的坐标为(x,y),若x=y,则点P在坐标平面内的位置是 ;若x+y=0,则点P在坐标平面内的位置是 ;
(2)已知点Q的坐标为(2﹣2a,a+8),且点Q到两坐标轴的距离相等,求点Q的坐标.
41.法定节日的确定为大家带来了很多便利.我们用坐标来表示这些节日:用A(1,1)表示元旦(即1月1日),清明节用B(4,4)表示(即4月4日),端午节用C(5,5)表示(即5月初5).
(1)请写出中秋节D( ),国庆节E( ).
(2)依次边结A﹣B﹣C﹣D﹣E﹣A,在坐标系中画出来.
(3)求出图形的面积.
42.已知点A(﹣8,0)及动点P(x,y),且2x﹣y=﹣6.设三角形OPA的面积为S.
(1)当x=﹣2时,点P坐标是 ;
(2)若点P在第二象限,且x为整数时,求y的值;
(3)是否存在第一象限的点P,使得S=12.若存在,求点P的坐标;若不存在,说明理由.
43.在如图所示的正方形网格中,每个小正方形的单位长度均为1,△ABC的三个顶点恰好是正方形网格的格点.
(1)写出图中所示△ABC各顶点的坐标.
(2)求出此三角形的面积.
44.如图,已知A(﹣2,3)、B(4,3)、C(﹣1,﹣3)
(1)求点C到x轴的距离;
(2)求△ABC的面积;
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
45.已知四边形ABCD各顶点的坐标分别是A(0,0),B(3,6),C(6,8),D(8,0)
(1)请建立适当的平面直角坐标系,并描出点A、点B、点C、点D.
(2)求四边形ABCD的面积.
46.如图,方格纸中小正方形的边长均为1个单位长度,A、B均为格点.
(1)在图中建立直角坐标系,使点A、B的坐标分别为(3,3)和(﹣1,0);
(2)在(1)中x轴上是否存在点C,使△ABC为等腰三角形(其中AB为腰)?若存在,请直接写出所有满足条件的点C的坐标.
参考答案
1.解:因为A1(﹣1,1),A2(2,1)
A3(﹣2,2)A4(3,2)
A5(﹣3,3)A6(4,3)
A7(﹣4,4)A8(5,4)
…
A2n﹣1(﹣n,n) A2n(n+1,n)(n为正整数)
所以2n=2020,
n=1010
所以A2020(1011,1010)
故选:D.
2.解:因为点M在第四象限,所以其横、纵坐标分别为正数、负数,
又因为点M到x轴的距离为6,到y轴的距离为4,
所以点M的坐标为(4,﹣6).
故选:A.
3.解:∵m2≥0,
∴m2+1>0,
∴点A(m,m2+1)不在第三、四象限.
故选:D.
4.解:由观察及归纳得到,箭头指向x轴的点从左到右依次为:0,3,4,15,16,35,36…
我们所关注的是所有偶数的平方均在x轴上,且坐标为k,便对应第k2个点,且从k2向上走k个点就转向左边,如22向上走2便转向;
箭头指向y轴的点依次为:0,1,8,9,24,25…
我们所关注的是所有奇数的平方均在y轴上,且坐标为k,便对应第k2个点,且从k2向右走k个点就转向下边,如
52向右走5便转向;
因为2020=442+84,所以先找到(44,0)这是第1936个点,还有84步,向上走44步左转,再走40步到达,距y轴有44﹣40=4个单位,所以第2020秒时质点所在位置的坐标是(4,44).
故选:D.
5.解:观察点的坐标变化发现:
当脚码为偶数时的点的坐标,得到规律:
当脚码是2、6、10…时,横坐标为1,纵坐标为脚码的一半的相反数,
当脚码是4、8、12.…时,横坐标是2,纵坐标为脚码的一半,
因为2020能被4整除,
所以横坐标为2,纵坐标为1010,
故选:D.
6.解:由图形可知:每条斜线上有点的个数与这条线段在x轴的交点的数一样,如图,
例如:线段AB上有两个点,线段CD上有5个点,
且发现x轴上奇数的点箭头方向向右,偶数的点箭头方向向左上线段上,
设x轴上的点(n,0),
1+2+3+4+…+n=,
当n=63时,=2016,
当n=64时,=2080,
∵2016<2019<2080,
∴第2016次时运动到达的点是(63,0),
∴则第2019次时运动到达的点为(62,2),
故选:D.
7.解:当k=1时,P1=(1,1);
当2≤k≤5时,P2,P3,P4,P5的坐标分别为(2,1)、(3,1)、(4,1)、(5,1);
当k=6时,P6=(1,2);
当7≤k≤10时,P7,P8,P9,P10的坐标分别为(2,2)、(3,2)、(4,2)、(5,2);
当k=11时,P11=(1,3);
当12≤k≤15时,P12,P13,P14,P15的坐标分别为(2,3)、(3,3)、(4,3)、(5,3)…
通过以上数据可以得出:当k=1+5x时,Pk的坐标为(1,x+1),而后面四个点的纵坐标均为x+1,横坐标则分别为2,3,4,5.因为2019=1+5×403+3,所以P2019的横坐标为4,纵坐标为404.
故选:B.
8.解:∵点M与点P关于y轴对称,点N与点M关于x轴对称,
∴点N与点P关于原点对称,
又∵点P的坐标为(﹣2,3),
∴点N的坐标为(2,﹣3),
故选:C.
9.解:由题可得,第2020次变换后的点M在x轴上方,
∴点M的纵坐标为2,横坐标为2﹣2020×1=﹣2018,
∴点M的坐标变为(﹣2018,2),
故选:A.
10.解:∵坐标平面内点A(﹣2,4),将坐标系先向左平移3个单位长度,再向上平移2个单位长度,
∴点A的横坐标增大3,纵坐标减小2,
∴点A变化后的坐标为(1,2).
故选:D.
11.解:由图可得,点A、B的对应点分别为点C、D,而B(1,3),D(2,0),
∴线段AB向右平移1个单位,向下平移3个单位得到线段CD,
又∵P(a,b),
∴Q(a+1,b﹣3),
故选:D.
12.解:如图所示,设直线OA为y=ax,则
由点A(1,2),可得2=a,
又∵平移后的直线两侧的格点数相同,
∴平移后的直线经过点B(2,3),
设直线BC的解析式为y=2x+b,则
由B(2,3),可得3=4+b,
解得b=﹣1,
∴y=2x﹣1,
令y=0,则x=,
即C(,0),
∴OC=,
∴k的值为,
故选:C.
13.解:∵点A关于x轴的对称点坐标为(﹣1,2),
∴点A坐标为(﹣1,﹣2);
∴点A关于原点的对称点的坐标为(1,2).
故选:A.
14.解:设P1(x,y),
∵点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点P2,
∴=1,=﹣1,
解得x=2,y=﹣4,
∴P1(2,﹣4).
同理可得,P2(﹣4,2),P3(4,0),P4(﹣2,﹣2),P5(0,0),P6(0,2),P7(2,﹣4),…,
∴每6个操作循环一次.
∵2018=6×336+2,
∴点P2018的坐标与P2(﹣4,2)相同.
故选:D.
15.解:∵三角形AOB是等腰直角三角形,点B的横坐标为4,
∴OA=AB,∠OAB=90°,OB=4,
∴OA=AB=2,
∴点A的坐标为(2,2),
∵等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,
∴点A′的坐标为(﹣2,2),
故选:C.
16.解:设G点移动距离为y,
当△CEG与△AFG全等时有:
∠FAG=∠ECG
CE=AF,CG=AG,或CE=AG,CG=AF
当F由B到A,即0<t≤3时,则有解得
或解得(舍去)
当F由A到B时,即3<t≤4(E由C到D)时,有解得(舍去)
或解得
当4<t≤6(E由D到C)时,12﹣(3t﹣12)=4t﹣12,解得t=.
故答案为或秒或秒.
17.解:如图所示,把△ABO经3次翻滚后,点B落到点B3处,点M经过点N、点H落到点M’处,点A落到点K处,作B3E⊥x轴于点E
则∠B3KE=60°,B3K=2
∴KE=B3K=1,B3E=B3K=
∴OE=2×2+1=5
∴B3(5,).
由图象可知,翻滚三次为一个循环
∵2018=3×672+2
∴翻滚2018次后AB中点M的纵坐标与点H的纵坐标相同
∵点H的纵坐标为0
∴翻滚2018次后AB中点M的纵坐标为0.
故答案为:(5,)、0.
18.解:由题意得,a﹣2=0,b+3=0,
解得a=2,b=﹣3,
所以,点P(﹣a,﹣b)即(﹣2,3)在第二象限.
故答案为:二.
19.解:如图,分别以点O和点A为圆心,2为半径画圆,
可得满足到点O和点A的距离都小于2的点是点M与点N,
故答案为:点M与点N.
20.解:若a,b同号,则﹣b,﹣a也同号且符号改变,此时点(﹣b,﹣a),点(a,b)分别在一三象限,不合题意;
若a,b异号,则﹣b,﹣a也异号,此时点(﹣b,﹣a),点(a,b)都在第二或第四象限,符合题意;
故答案为:二、四.
21.解:半径为1个单位长度的半圆的周长为×2π×1=π,
∵点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,
∴点P每秒走个半圆,
当点P从原点O出发,沿这条曲线向右运动,运动时间为1秒时,点P的坐标为(1,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为2秒时,点P的坐标为(2,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为3秒时,点P的坐标为(3,﹣1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为4秒时,点P的坐标为(4,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为5秒时,点P的坐标为(5,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为6秒时,点P的坐标为(6,0),
…,
∵2021÷4=505余1,
∴P的坐标是(2021,1),
故答案为:(2021,1).
22.解:(1)观察各点规律发现:
第1、4、7、10个点在x轴上,偶数是负号,奇数是正号,
坐标分别(1,0),(﹣2,0),(3,0),(﹣4,0),…,
第2、5、8个点在y轴上,偶数是负号,奇数是正号,
坐标分别(0,1),(0,﹣2),(0,3),…,
第3、6、9个点在一三象限,
坐标分别(1,1),(﹣2,﹣2),(3,3),…,
∵1000÷3=333余1,
∴第1000个点在x轴负半轴上,坐标为(﹣334,0).
故答案为:(﹣334,0).
23.解:∵正方形ABCD的边长为8,
∴CD=DA=BC=AB=8,
∵M(0,5),C(6,﹣3),
∴A(﹣2,5),B(6,5),D(﹣2,﹣3),
∴AM=2,BM=6,
∴绕正方形ABCD一周的细线长度为8×4=32,
∵2020÷32=63…4,
∴细线另一端在绕正方形第63圈的第4个单位长度的位置,
即在AB边或在AD边上,
∴点N的坐标为(﹣2,3)或(4,5).
故答案为:(﹣2,3)或(4,5).
24.解:∵点E(a﹣1,a),F(b,a﹣b),
∴中点G(,),
∵中点G恰好位于x轴上,且到y轴的距离是2,
∴,
解得:,,
∴2a+b=或﹣4;
故答案为:或﹣4.
25.解:如图,当y轴平分∠APB时,点A关于y轴的对称点A'在BP上,
∵A(1,2),
∴A'(﹣1,2),
设A'B的表达式为y=kx+b,
把A'(﹣1,2),B(﹣3,1)代入,
可得,
解得k=,b=,
∴y=x+,
令x=0,则y=,
∴点P的坐标为(0,),
故答案为:(0,).
26.解:∵AB∥x轴,点A的坐标为(2,5),
∴点B的纵坐标为5,
∵AB=4,
∴点B的横坐标为2﹣4=﹣2,或2+4=6,
∴点B的坐标为(6,5)或(﹣2,5)
故答案为:(6,5)或(﹣2,5)).
27.解:点A(a,﹣3)向左平移3个单位后为(a﹣3,﹣3),
∵所得的点A'与点A关于y轴对称,
∴a﹣3=﹣a,
解得a=1.5.
故答案为:1.5.
28.解:∵P关于x轴的对称点为(3,a),
∴点P的横坐标为3;
∵P关于y轴对称的点为(b,2),
∴点P的纵坐标为2,
∴P点的坐标为(3,2).
故答案为:(3,2).
29.解:∵△ABO关于x轴对称,点A的坐标为(1,﹣2),
∴点B的坐标为(1,2),
又∵在坐标轴上有一个点P,满足△BOP的面积等于2,
∴当点P在x轴上时,×OP×2=2,即OP=2,
当点P在y轴上时,×OP×1=2,即OP=4,
∴点P的坐标为(﹣2,0),(2,0),(0,4),(0,﹣4),
故答案为:(﹣2,0),(2,0),(0,4),(0,﹣4).
30.解:根据题意,点A和点B是关于直线y=1对称的对应点,
∴它们到y=1的距离相等,是3个单位长度,AB⊥x轴,
∴点B的坐标是(4,﹣2).
若△ABC是关于直线y=a的轴对称图形,则点B的横坐标为4,纵坐标为a﹣(4﹣a)=2a﹣4,
∴点B的坐标为(4,2a﹣4),
故答案为:(4,﹣2),(4,2a﹣4).
31.解:x1+x2+x3+x4=1﹣1﹣1+3=2;
x5+x6+x7+x8=3﹣3﹣3+5=2;
…
x97+x98+x99+x100=2;
∴原式=2×(100÷4)=50.
32.(1)解:如图所示:
∵点P4与P重合,
∴点P4与点P1的距离是60cm+60cm=120cm,
(2)解:25÷4=6…1,第一次休息点在P1,
25÷4=6…1,第二次休息点在P2,
25÷4=6…1,第三次休息点在P3,
即P3与点P的距离是30cm+30cm=60cm.
答:电子青蛙第三次休息点与点P的距离是60cm.
33.解:(1)已知A(1,3),A1(3,3),A2(5,3),A3(7,3);
对于A1,A2,An坐标找规律比较从而发现An的横坐标为2n+1,而纵坐标都是3;
同理B1,B2,Bn也一样找规律,规律为Bn的横坐标为2n+1,纵坐标为0.
由上规律可知:(1)A4的坐标是(9,3),B4的坐标是(32,0);
(2)An的坐标是(2n+1,3),Bn的坐标是(2n+1,0)
34.解:(1)由图示可知各点的坐标为:A(1,0),B(2,1),C(2,2);
(2)如图:
(3)设射线OD上点K的横、纵坐标满足的关系式为y=kx;
由图知:D(1,2),则:k=2,
即x与y所满足的关系式为:y=2x(x≥0).
35.解:(1)由已知|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0及(c﹣4)2≥0
可得:a=2,b=3,c=4;
(2)∵×2×3=3,×2×(﹣m)=﹣m,
∴S四边形ABOP=S△ABO+S△APO=3+(﹣m)=3﹣m
(3)因为×4×3=6,
∵S四边形ABOP=S△ABC
∴3﹣m=6,
则 m=﹣3,
所以存在点P(﹣3,)使S四边形ABOP=S△ABC.
36.解:(1)依据两点间的距离公式,可得AB==13;
(2)当点A,B在平行于y轴的直线上时,AB=|﹣1﹣5|=6;
(3)AB与AC相等.理由:
∵AB==5;
AC==5;
BC=|3﹣(﹣3)|=6.
∴AB=AC.
37.解:(1)如图,过D作DE⊥x轴,垂足为E,过C作CF⊥x轴,垂足为F,
∴S四边形ABCD=S△ADE+S四边形DEFC+S△CFB
∵S△ADE=×1×4=2,
S四边形DEFC=(3+4)×1=,
S△CFB=×2×3=3,
∴S四边形ABCD=2++3=;
(2)由题可得,四边形ABCD先向左平移3个单位,再向下平移1个单位得四边形A′B′C′D',
∴平移后,各顶点的横坐标减小3,纵坐标减小1,
∵A(1,0)、B(5,0)、C(3,3),D(2,4),
∴A′(﹣2,﹣1),B′(2,﹣1),C′(0,2),D′(﹣1,3).
38.解:(1)当c=0时,a、b满足:a﹣2b=﹣1,2a﹣3b=﹣4,
解得a=﹣5,b=﹣2,
∴A点的坐标为(5,﹣5),B点的坐标为(﹣2,0);
(2)∠EDC=∠ABC+∠ACB.
证明:如图,延长BA至G,
由平移得,AB∥DE,
∴∠EDC=∠GAC,
又∵∠GAC是△ABC的外角,
∴∠GAC=∠ABC+∠ACB,
∴∠EDC=∠ABC+∠ACB;
(3)如图,∵坐标原点O与点A对应,且A(5,﹣5),
∴线段AB向上平移5个单位,再向左平移5个单位,可平移到OF处,
又∵F与B对应,且B(﹣2,0),
∴F点的横坐标为:﹣2﹣5=﹣7,纵坐标为:0+5=5,
∴F点的坐标为(﹣7,5).
39.解:(1)1﹣a=﹣3,a=4.
(2)由a=4得:2a﹣12=2×4﹣12=﹣4,又点Q(x,y)位于第二象限,所以y>0;
取y=1,得点Q的坐标为(﹣4,1).
(3)因为点P(2a﹣12,1﹣a)位于第三象限,
所以,
解得:1<a<6.
因为点P的横、纵坐标都是整数,所以a=2或3或4或5;
当a=2时,1﹣a=﹣1,所以PQ>1;
当a=3时,1﹣a=﹣2,所以PQ>2;
当a=4时,1﹣a=﹣3,所以PQ>3;
当a=5时,1﹣a=﹣4,所以PQ>4.
40.解:(1)∵点P的坐标为(x,y),若x=y,
∴点P在一、三象限内两坐标轴夹角的平分线上.
∵x+y=0,
∴x、y互为相反数,
∴P点在二、四象限内两坐标轴夹角的平分线上.
故答案为:在一、三象限内两坐标轴夹角的平分线上.在二、四象限内两坐标轴夹角的平分线上.
(2)∵点Q到两坐标轴的距离相等,
∴|2﹣2a|=|8+a|,
∴2﹣2a=8+a或2﹣2a=﹣8﹣a,
解得a=﹣2或a=10,
当a=﹣2时,2﹣2a=2﹣2×(﹣2)=6,8+a=8﹣2=6,
当a=10时,2﹣2a=2﹣20=﹣18,8+a=8+10=18,
所以,点Q的坐标为(6,6)或(﹣18,18).
41.解:(1)中秋节D(8,15),国庆节E(10,1).
(2)如图.
(3)将图形补成一个矩形AEFG
则:S长AEFG=9×14=126
S△DEF==14
S△ACH==8
S梯形CDGH=(4+7)×=55
S四AEDC=126﹣14﹣8﹣55=49
答:该图形的面积为49.
42.解:(1)把x=﹣2代入2x﹣y=﹣6,得
2×(﹣2)﹣y=﹣6,
解得y=2,
所以,点P坐标是(﹣2,2).
故答案是:(﹣2,2).
(2)∵2x﹣y=﹣6,
∴y=2x+6.
∵点P在第二象限,
∴得﹣3<x<0.
又∵x是整数
∴x=﹣1,﹣2.
当x=﹣1时,y=4;
当x=﹣2时,y=2.
(3)不存在.理由如下:
如图,
∵点P在第一象限,
作PQ⊥x轴,垂足为Q,则PQ=2x+6,
又∵OA=0﹣(﹣8)=8,
∴S=×OA×PQ=12,即×8×(2x+6)=12,得x=,此时点P的坐标为(,3).
∴点P不在第一象限,即不存在这样的点P.
43.解:(1)A(3,3),B(﹣2,﹣2),C(4,﹣3);
(2)如图所示:
S△ABC=S矩形DECF﹣S△BEC﹣S△ADB﹣S△AFC
==.
44.解:(1)∵C(﹣1,﹣3),
∴|﹣3|=3,
∴点C到x轴的距离为3;
(2)∵A(﹣2,3)、B(4,3)、C(﹣1,﹣3)
∴AB=4﹣(﹣2)=6,点C到边AB的距离为:3﹣(﹣3)=6,
∴△ABC的面积为:6×6÷2=18.
(3)设点P的坐标为(0,y),
∵△ABP的面积为6,A(﹣2,3)、B(4,3),
∴6×|y﹣3|=6,
∴|y﹣3|=2,
∴y=1或y=5,
∴P点的坐标为(0,1)或(0,5).
45.解:(1)如图所示.
(2)过B作BE⊥AD于E,过C作CF⊥AD于F,则
S四边形ABCD=S△ABE+S梯形BEFC+S△CFD
=
=
=9+21+8
=38
答:四边形ABCD的面积为38.
46.解:(1)如图:直角坐标系即为所求;
(2)存在点C,使△ABC为等腰三角形,如图,
∵AB==5,
∵以AB为腰,
∴AC4=BC4,舍去,
∴所有满足条件的点C的坐标为C(7,0)或C′(4,0)或C″(﹣6,0).
1.如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(﹣2,2),第四次向右跳动5个单位至点A4(3,2),…,以此规律跳动下去,点A第2020次跳动至点A2020的坐标是( )
A.(1012,1011) B.(1009,1008)
C.(1010,1009) D.(1011,1010)
2.在平面直角坐标系中,点M在第四象限,到x轴,y轴的距离分别为6,4,则点M的坐标为( )
A.(4,﹣6) B.(﹣4,6) C.(﹣6,4) D.(﹣6,﹣4)
3.已知m为任意实数,则点A(m,m2+1)不在( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限
4. 一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动,且每秒移动一个单位,那么第2020秒时质点所在位置的坐标是( )
A.(4,16) B.(44,44) C.(44,4) D.(4,44)
5.如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7……,都是斜边在x轴上,斜边长分别为2,4,6,……的等腰直角三角形,若A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2020的坐标为( )
A.(1010,0) B.(1012,0) C.(2,1012) D.(2,1010)
6.如图,一个粒子在x轴上及第一象限内运动,第1次从(0,0)运动到(1,0),第2次从(1,0)运动到(2,0),第3次从(2,0)运动到(1,1),它接着按图中箭头所示的方向运动.则第2019次时运动到达的点为( )
A.(59,6) B.(59,5) C.(62,3) D.(62,2)
7.我校“心动数学”社团活动小组,在网格纸上为学校的一块空地设计植树方案如下:
第k棵树种植在点第xk行yk列处,其中x1=1,y1=1,当k≥2时,
,
[a]表示非负数a的整数部分,例如[2.6]=2,[0.2]=0.按此方案,第2019棵树种植点所在的行数是4,则所在的列数是( )
A.403 B.404 C.2019 D.2020
8.在平面直角坐标系中,点P与点M关于y轴对称,点N与点M关于x轴对称,若点P的坐标为(﹣2,3),则点N的坐标为( )
A.(﹣3,2) B.(2,3) C.(2,﹣3) D.(﹣2,﹣3)
9.已知M(2,2).规定“把点M先作关于x轴对称,再向左平移1个单位”为一次变换.那么连续经过2020次变换后,点M的坐标变为( )
A.(﹣2018,2) B.(﹣2018,﹣2) C.(﹣2019,﹣2) D.(﹣2019,2)
10.已知坐标平面内的点A(﹣2,4),如果将平面直角坐标系向左平移3个单位长度,再向上平移2个单位长度,那么平移后点A的坐标是( )
A.(1,6) B.(﹣5,6) C.(﹣5,2) D.(1,2)
11.线段AB经过平移得到线段CD,其中点A、B的对应点分别为点C、D,这四个点都在如图所示的格点上,那么线段AB上的一点P(a,b)经过平移后,在线段CD上的对应点Q的坐标是( )
A.(a﹣1,b+3) B.(a﹣1,b﹣3) C.(a+1,b+3) D.(a+1,b﹣3)
12.如图,在平面直角坐标系中有一个2×2的正方形网格,每个格点的横、纵坐标均为整数,已知点A(1,2),作直线OA并向右平移k个单位,要使分布在平移后的直线两侧的格点数相同,则k的值为( )
A. B. C. D.1
13.已知点A关于x轴的对称点坐标为(﹣1,2),则点A关于原点的对称点的坐标为( )
A.(1,2) B.(﹣1,﹣2) C.(2,﹣1) D.(1,﹣2)
14.在平面直角坐标系中有三个点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点P2,P2关于C的对称点为P3,按此规律继续以A、B、C为对称中心重复前面的操作,依次得到P4,P5,P6,…,则点P2018的坐标是( )
A.(0,0) B.(0,2) C.(2,﹣4) D.(﹣4,2)
15.在平面直角坐标系xOy中,将等腰直角三角形AOB按如图所示的位置放置,然后绕原点O逆时针旋转90°到△A'OB'的位置,若点B的坐标为B(4,0),则点A'的坐标为( )
A.(2,2) B.(2,2) C.(﹣2,2) D.(﹣2,2)
16.如图,在平面直角坐标系内,点A、点B的坐标分别为A(﹣7,0),B(5,0),现将线段AB向上平移9个单位,得到对应线段DC,连接AD、BC、AC,若AC=15,动点E从C点出发,以每秒3个单位的速度沿C→D→C作匀速移动,点F从点B出发,以每秒4个单位的速度沿B→A→B作匀速运动,点G从点A出发沿AC向点C匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.在移动过程中,若△CEG与△AFG全等,则此时的移动时间t的值为 .
17.如图,等边三角形ABO的边长为2,O为坐标原点,A在x轴上,B在第二象限.△ABO沿x轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是 ;翻滚2018次后AB中点M的纵坐标为 .
18.已知(a﹣2)2+|b+3|=0,则点P(﹣a,﹣b)在第 象限.
19.如图,在平面直角坐标系xOy中,点A(3,0),判断在M,N,P,Q四点中,满足到点O和点A的距离都小于2的点是 .
20.在平面直角坐标系中,将点(﹣b,﹣a)称为点(a,b)的“关联点”(例如点(﹣2,﹣1)是点(1,2)的“关联点”).如果一个点和它的“关联点”在同一象限内,那么这一点在第 象限.
21.如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2021秒时,点P的坐标是 .
22.在直角坐标系中,下面各点按顺序依次排列:(1,0),(0,1),(1,1),(﹣2,0),(0,﹣2),(﹣2,﹣2),(3,0),(0,3),(3,3),(﹣4,0),(0,﹣4),(﹣4,﹣4)…,按此规律,这列点中第1000个点的坐标是 .
23.如图,在平面直角坐标系中,已知正方形ABCD的边长为8,与y轴交于点M(0,5),顶点C(6,﹣3),将一条长为2020个单位长度且没有弹性的细绳一端固定在点M处,从点M出发将细绳紧绕在正方形ABCD的边上,则细绳的另一端到达的位置点N的坐标为 .
24.教材上曾让同学们探索过线段的中点坐标:在平面直角坐标系中,若两点A(x1,y1)、B(x2,y2),所连线段AB的中点是M,则M的坐标为(,),例如:点A(1,2)、点B(3,6),则线段AB的中点M的坐标为(,),即M(2,4)请利用以上结论解决问题:在平面直角坐标系中,若点E(a﹣1,a),F(b,a﹣b),线段EF的中点G恰好位于x轴上,且到y轴的距离是2,则2a+b的值等于 .
25.已知A(1,2)、B(﹣3,1),点P在y轴上,则当y轴平分∠APB时,点P的坐标为 .
26.已知AB∥x轴,点A的坐标为(2,5),并且AB=4,则点B的坐标为 .
27.在平面直角坐标系中,点A(a,﹣3)向左平移3个单位得点A′,若点A和A′关于y轴对称,则a= .
28.若P关于x轴的对称点为(3,a),关于y轴对称的点为(b,2),则P点的坐标为 .
29.已知△ABO关于x轴对称,点A的坐标为(1,﹣2),若在坐标轴上有一个点P,满足△BOP的面积等于2,则点P的坐标为 .
30.如图,在平面直角坐标系中,已知点A的坐标为(4,4),若△ABC是关于直线y=1的轴对称图形,则点B的坐标为 ;若△ABC是关于直线y=a的轴对称图形,则点B的坐标为 .
31.如图,在直角坐标系中,设一动点M自P0(1,0)处向上运动1个单位至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn,yn),n=1,2,3,…则x1+x2+…+x99+x100= .
32.我们规定:若点O是线段MN的中点,则称点M关于O的对称点是N(或称点M与点N关于O成中心对称);若直线n是线段MN的垂直平分线,则称点M关于n的对称点是N(或称点M与点N关于n成轴对称),如图现有石头A和石头B关于竹竿l对称,石头A和石头B相距80cm一只电子青蛙位于点P,与石头A相距60cm,与竹竿l相距30cm,他按照如下指令跳动:第一跳落点于P1,P与P1关于点A成中心对称;第二跳落点于P2,P2与P1关于竹竿l成轴对称;第三跳落点于P3,P3与P2关于点B成中心对称;第四跳落点于P4,P4与P3关于竹竿l成轴对称;以此跃下去,若每25跳可以休息一次.
(1)画出这只电子青蛙前四跳运动的路线图,并求点P4与点P1的距离(不须说明理由)
(2)求电子青蛙第三次休息点与点P的距离.
33.如图:在直角坐标系中,第一次将△AOB变换成△OA1B1,第二次将三角形变换成△OA2B2,第三次将△OA2B2,变换成△OA3B3,已知A(1,3),A1(3,3),A2(5,3),A3(7,3);B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此变化规律再将△OA3B3变换成△OA4B4,则A4的坐标是 ,B4的坐标是 .
(2)若按(1)找到的规律将△OAB进行了n次变换,得到△OAnBn,比较每次变换中三角形顶点有何变化,找出规律,推测An的坐标是 ,Bn的坐标是 .
34.小明在研究苏教版《有趣的坐标系》后,得到启发,针对正六边形OABCDE,自己设计了一个坐标系如图,该坐标系以O为原点,直线OA为x轴,直线OE为y轴,以正六边形OABCDE的边长为一个单位长.坐标系中的任意一点P用一有序实数对(a,b)来表示,我们称这个有序实数对(a,b)为点P的坐标.坐标系中点的坐标的确定方法如下:
(ⅰ)x轴上点M的坐标为(m,0),其中m为M点在x轴上表示的实数;
(ⅱ)y轴上点N的坐标为(0,n),其中n为N点在y轴上表示的实数;
(ⅲ)不在x、y轴上的点Q的坐标为(a,b),其中a为过点Q且与y轴平行的直线与x轴的交点在x轴上表示的实数,b为过点Q且与x轴平行的直线与y轴的交点在y轴上表示的实数.
则:(1)分别写出点A、B、C的坐标;
(2)标出点M(2,3)的位置;
(3)若点K(x,y)为射线OD上任一点,求x与y所满足的关系式.
35.如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
36.先阅读下列一段文字,再解答问题
已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|
(1)已知点A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点间的距离;
(3)已知点A(0,6)B(﹣3,2),C(3,2),判断线段AB,BC,AC中哪两条是相等的?并说明理由.
37.在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,0)、B(5,0)、C(3,3),D(2,4).
(1)求:四边形ABCD的面积.
(2)如果把四边形ABCD先向左平移3个单位,再向下平移1个单位得四边形A′B′C′D',求A',B′,C',D′点坐标.
38.已知在平面直角坐标系中,A(﹣a,a),a≠0,B(b,c),a、b、c满足a﹣2b﹣3c=﹣1,2a﹣3b﹣5c=﹣4.
(1)若c=0,求A、B两点的坐标;
(2)在(1)的条件下,C(m,0)为一动点,且m>0,连接AB、AC,平移线段AB得到线段ED,使B点的对应点D落在线段AC上,则∠EDC、∠ABC、∠ACB之间有何数量关系?证明你的结论;
(3)若将线段AB平移到OF处,点F在第二象限,坐标原点O与点A对应,F与B对应,求F点的坐标.
39.已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值;
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
40.(1)点P的坐标为(x,y),若x=y,则点P在坐标平面内的位置是 ;若x+y=0,则点P在坐标平面内的位置是 ;
(2)已知点Q的坐标为(2﹣2a,a+8),且点Q到两坐标轴的距离相等,求点Q的坐标.
41.法定节日的确定为大家带来了很多便利.我们用坐标来表示这些节日:用A(1,1)表示元旦(即1月1日),清明节用B(4,4)表示(即4月4日),端午节用C(5,5)表示(即5月初5).
(1)请写出中秋节D( ),国庆节E( ).
(2)依次边结A﹣B﹣C﹣D﹣E﹣A,在坐标系中画出来.
(3)求出图形的面积.
42.已知点A(﹣8,0)及动点P(x,y),且2x﹣y=﹣6.设三角形OPA的面积为S.
(1)当x=﹣2时,点P坐标是 ;
(2)若点P在第二象限,且x为整数时,求y的值;
(3)是否存在第一象限的点P,使得S=12.若存在,求点P的坐标;若不存在,说明理由.
43.在如图所示的正方形网格中,每个小正方形的单位长度均为1,△ABC的三个顶点恰好是正方形网格的格点.
(1)写出图中所示△ABC各顶点的坐标.
(2)求出此三角形的面积.
44.如图,已知A(﹣2,3)、B(4,3)、C(﹣1,﹣3)
(1)求点C到x轴的距离;
(2)求△ABC的面积;
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
45.已知四边形ABCD各顶点的坐标分别是A(0,0),B(3,6),C(6,8),D(8,0)
(1)请建立适当的平面直角坐标系,并描出点A、点B、点C、点D.
(2)求四边形ABCD的面积.
46.如图,方格纸中小正方形的边长均为1个单位长度,A、B均为格点.
(1)在图中建立直角坐标系,使点A、B的坐标分别为(3,3)和(﹣1,0);
(2)在(1)中x轴上是否存在点C,使△ABC为等腰三角形(其中AB为腰)?若存在,请直接写出所有满足条件的点C的坐标.
参考答案
1.解:因为A1(﹣1,1),A2(2,1)
A3(﹣2,2)A4(3,2)
A5(﹣3,3)A6(4,3)
A7(﹣4,4)A8(5,4)
…
A2n﹣1(﹣n,n) A2n(n+1,n)(n为正整数)
所以2n=2020,
n=1010
所以A2020(1011,1010)
故选:D.
2.解:因为点M在第四象限,所以其横、纵坐标分别为正数、负数,
又因为点M到x轴的距离为6,到y轴的距离为4,
所以点M的坐标为(4,﹣6).
故选:A.
3.解:∵m2≥0,
∴m2+1>0,
∴点A(m,m2+1)不在第三、四象限.
故选:D.
4.解:由观察及归纳得到,箭头指向x轴的点从左到右依次为:0,3,4,15,16,35,36…
我们所关注的是所有偶数的平方均在x轴上,且坐标为k,便对应第k2个点,且从k2向上走k个点就转向左边,如22向上走2便转向;
箭头指向y轴的点依次为:0,1,8,9,24,25…
我们所关注的是所有奇数的平方均在y轴上,且坐标为k,便对应第k2个点,且从k2向右走k个点就转向下边,如
52向右走5便转向;
因为2020=442+84,所以先找到(44,0)这是第1936个点,还有84步,向上走44步左转,再走40步到达,距y轴有44﹣40=4个单位,所以第2020秒时质点所在位置的坐标是(4,44).
故选:D.
5.解:观察点的坐标变化发现:
当脚码为偶数时的点的坐标,得到规律:
当脚码是2、6、10…时,横坐标为1,纵坐标为脚码的一半的相反数,
当脚码是4、8、12.…时,横坐标是2,纵坐标为脚码的一半,
因为2020能被4整除,
所以横坐标为2,纵坐标为1010,
故选:D.
6.解:由图形可知:每条斜线上有点的个数与这条线段在x轴的交点的数一样,如图,
例如:线段AB上有两个点,线段CD上有5个点,
且发现x轴上奇数的点箭头方向向右,偶数的点箭头方向向左上线段上,
设x轴上的点(n,0),
1+2+3+4+…+n=,
当n=63时,=2016,
当n=64时,=2080,
∵2016<2019<2080,
∴第2016次时运动到达的点是(63,0),
∴则第2019次时运动到达的点为(62,2),
故选:D.
7.解:当k=1时,P1=(1,1);
当2≤k≤5时,P2,P3,P4,P5的坐标分别为(2,1)、(3,1)、(4,1)、(5,1);
当k=6时,P6=(1,2);
当7≤k≤10时,P7,P8,P9,P10的坐标分别为(2,2)、(3,2)、(4,2)、(5,2);
当k=11时,P11=(1,3);
当12≤k≤15时,P12,P13,P14,P15的坐标分别为(2,3)、(3,3)、(4,3)、(5,3)…
通过以上数据可以得出:当k=1+5x时,Pk的坐标为(1,x+1),而后面四个点的纵坐标均为x+1,横坐标则分别为2,3,4,5.因为2019=1+5×403+3,所以P2019的横坐标为4,纵坐标为404.
故选:B.
8.解:∵点M与点P关于y轴对称,点N与点M关于x轴对称,
∴点N与点P关于原点对称,
又∵点P的坐标为(﹣2,3),
∴点N的坐标为(2,﹣3),
故选:C.
9.解:由题可得,第2020次变换后的点M在x轴上方,
∴点M的纵坐标为2,横坐标为2﹣2020×1=﹣2018,
∴点M的坐标变为(﹣2018,2),
故选:A.
10.解:∵坐标平面内点A(﹣2,4),将坐标系先向左平移3个单位长度,再向上平移2个单位长度,
∴点A的横坐标增大3,纵坐标减小2,
∴点A变化后的坐标为(1,2).
故选:D.
11.解:由图可得,点A、B的对应点分别为点C、D,而B(1,3),D(2,0),
∴线段AB向右平移1个单位,向下平移3个单位得到线段CD,
又∵P(a,b),
∴Q(a+1,b﹣3),
故选:D.
12.解:如图所示,设直线OA为y=ax,则
由点A(1,2),可得2=a,
又∵平移后的直线两侧的格点数相同,
∴平移后的直线经过点B(2,3),
设直线BC的解析式为y=2x+b,则
由B(2,3),可得3=4+b,
解得b=﹣1,
∴y=2x﹣1,
令y=0,则x=,
即C(,0),
∴OC=,
∴k的值为,
故选:C.
13.解:∵点A关于x轴的对称点坐标为(﹣1,2),
∴点A坐标为(﹣1,﹣2);
∴点A关于原点的对称点的坐标为(1,2).
故选:A.
14.解:设P1(x,y),
∵点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点P2,
∴=1,=﹣1,
解得x=2,y=﹣4,
∴P1(2,﹣4).
同理可得,P2(﹣4,2),P3(4,0),P4(﹣2,﹣2),P5(0,0),P6(0,2),P7(2,﹣4),…,
∴每6个操作循环一次.
∵2018=6×336+2,
∴点P2018的坐标与P2(﹣4,2)相同.
故选:D.
15.解:∵三角形AOB是等腰直角三角形,点B的横坐标为4,
∴OA=AB,∠OAB=90°,OB=4,
∴OA=AB=2,
∴点A的坐标为(2,2),
∵等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,
∴点A′的坐标为(﹣2,2),
故选:C.
16.解:设G点移动距离为y,
当△CEG与△AFG全等时有:
∠FAG=∠ECG
CE=AF,CG=AG,或CE=AG,CG=AF
当F由B到A,即0<t≤3时,则有解得
或解得(舍去)
当F由A到B时,即3<t≤4(E由C到D)时,有解得(舍去)
或解得
当4<t≤6(E由D到C)时,12﹣(3t﹣12)=4t﹣12,解得t=.
故答案为或秒或秒.
17.解:如图所示,把△ABO经3次翻滚后,点B落到点B3处,点M经过点N、点H落到点M’处,点A落到点K处,作B3E⊥x轴于点E
则∠B3KE=60°,B3K=2
∴KE=B3K=1,B3E=B3K=
∴OE=2×2+1=5
∴B3(5,).
由图象可知,翻滚三次为一个循环
∵2018=3×672+2
∴翻滚2018次后AB中点M的纵坐标与点H的纵坐标相同
∵点H的纵坐标为0
∴翻滚2018次后AB中点M的纵坐标为0.
故答案为:(5,)、0.
18.解:由题意得,a﹣2=0,b+3=0,
解得a=2,b=﹣3,
所以,点P(﹣a,﹣b)即(﹣2,3)在第二象限.
故答案为:二.
19.解:如图,分别以点O和点A为圆心,2为半径画圆,
可得满足到点O和点A的距离都小于2的点是点M与点N,
故答案为:点M与点N.
20.解:若a,b同号,则﹣b,﹣a也同号且符号改变,此时点(﹣b,﹣a),点(a,b)分别在一三象限,不合题意;
若a,b异号,则﹣b,﹣a也异号,此时点(﹣b,﹣a),点(a,b)都在第二或第四象限,符合题意;
故答案为:二、四.
21.解:半径为1个单位长度的半圆的周长为×2π×1=π,
∵点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,
∴点P每秒走个半圆,
当点P从原点O出发,沿这条曲线向右运动,运动时间为1秒时,点P的坐标为(1,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为2秒时,点P的坐标为(2,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为3秒时,点P的坐标为(3,﹣1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为4秒时,点P的坐标为(4,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为5秒时,点P的坐标为(5,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为6秒时,点P的坐标为(6,0),
…,
∵2021÷4=505余1,
∴P的坐标是(2021,1),
故答案为:(2021,1).
22.解:(1)观察各点规律发现:
第1、4、7、10个点在x轴上,偶数是负号,奇数是正号,
坐标分别(1,0),(﹣2,0),(3,0),(﹣4,0),…,
第2、5、8个点在y轴上,偶数是负号,奇数是正号,
坐标分别(0,1),(0,﹣2),(0,3),…,
第3、6、9个点在一三象限,
坐标分别(1,1),(﹣2,﹣2),(3,3),…,
∵1000÷3=333余1,
∴第1000个点在x轴负半轴上,坐标为(﹣334,0).
故答案为:(﹣334,0).
23.解:∵正方形ABCD的边长为8,
∴CD=DA=BC=AB=8,
∵M(0,5),C(6,﹣3),
∴A(﹣2,5),B(6,5),D(﹣2,﹣3),
∴AM=2,BM=6,
∴绕正方形ABCD一周的细线长度为8×4=32,
∵2020÷32=63…4,
∴细线另一端在绕正方形第63圈的第4个单位长度的位置,
即在AB边或在AD边上,
∴点N的坐标为(﹣2,3)或(4,5).
故答案为:(﹣2,3)或(4,5).
24.解:∵点E(a﹣1,a),F(b,a﹣b),
∴中点G(,),
∵中点G恰好位于x轴上,且到y轴的距离是2,
∴,
解得:,,
∴2a+b=或﹣4;
故答案为:或﹣4.
25.解:如图,当y轴平分∠APB时,点A关于y轴的对称点A'在BP上,
∵A(1,2),
∴A'(﹣1,2),
设A'B的表达式为y=kx+b,
把A'(﹣1,2),B(﹣3,1)代入,
可得,
解得k=,b=,
∴y=x+,
令x=0,则y=,
∴点P的坐标为(0,),
故答案为:(0,).
26.解:∵AB∥x轴,点A的坐标为(2,5),
∴点B的纵坐标为5,
∵AB=4,
∴点B的横坐标为2﹣4=﹣2,或2+4=6,
∴点B的坐标为(6,5)或(﹣2,5)
故答案为:(6,5)或(﹣2,5)).
27.解:点A(a,﹣3)向左平移3个单位后为(a﹣3,﹣3),
∵所得的点A'与点A关于y轴对称,
∴a﹣3=﹣a,
解得a=1.5.
故答案为:1.5.
28.解:∵P关于x轴的对称点为(3,a),
∴点P的横坐标为3;
∵P关于y轴对称的点为(b,2),
∴点P的纵坐标为2,
∴P点的坐标为(3,2).
故答案为:(3,2).
29.解:∵△ABO关于x轴对称,点A的坐标为(1,﹣2),
∴点B的坐标为(1,2),
又∵在坐标轴上有一个点P,满足△BOP的面积等于2,
∴当点P在x轴上时,×OP×2=2,即OP=2,
当点P在y轴上时,×OP×1=2,即OP=4,
∴点P的坐标为(﹣2,0),(2,0),(0,4),(0,﹣4),
故答案为:(﹣2,0),(2,0),(0,4),(0,﹣4).
30.解:根据题意,点A和点B是关于直线y=1对称的对应点,
∴它们到y=1的距离相等,是3个单位长度,AB⊥x轴,
∴点B的坐标是(4,﹣2).
若△ABC是关于直线y=a的轴对称图形,则点B的横坐标为4,纵坐标为a﹣(4﹣a)=2a﹣4,
∴点B的坐标为(4,2a﹣4),
故答案为:(4,﹣2),(4,2a﹣4).
31.解:x1+x2+x3+x4=1﹣1﹣1+3=2;
x5+x6+x7+x8=3﹣3﹣3+5=2;
…
x97+x98+x99+x100=2;
∴原式=2×(100÷4)=50.
32.(1)解:如图所示:
∵点P4与P重合,
∴点P4与点P1的距离是60cm+60cm=120cm,
(2)解:25÷4=6…1,第一次休息点在P1,
25÷4=6…1,第二次休息点在P2,
25÷4=6…1,第三次休息点在P3,
即P3与点P的距离是30cm+30cm=60cm.
答:电子青蛙第三次休息点与点P的距离是60cm.
33.解:(1)已知A(1,3),A1(3,3),A2(5,3),A3(7,3);
对于A1,A2,An坐标找规律比较从而发现An的横坐标为2n+1,而纵坐标都是3;
同理B1,B2,Bn也一样找规律,规律为Bn的横坐标为2n+1,纵坐标为0.
由上规律可知:(1)A4的坐标是(9,3),B4的坐标是(32,0);
(2)An的坐标是(2n+1,3),Bn的坐标是(2n+1,0)
34.解:(1)由图示可知各点的坐标为:A(1,0),B(2,1),C(2,2);
(2)如图:
(3)设射线OD上点K的横、纵坐标满足的关系式为y=kx;
由图知:D(1,2),则:k=2,
即x与y所满足的关系式为:y=2x(x≥0).
35.解:(1)由已知|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0及(c﹣4)2≥0
可得:a=2,b=3,c=4;
(2)∵×2×3=3,×2×(﹣m)=﹣m,
∴S四边形ABOP=S△ABO+S△APO=3+(﹣m)=3﹣m
(3)因为×4×3=6,
∵S四边形ABOP=S△ABC
∴3﹣m=6,
则 m=﹣3,
所以存在点P(﹣3,)使S四边形ABOP=S△ABC.
36.解:(1)依据两点间的距离公式,可得AB==13;
(2)当点A,B在平行于y轴的直线上时,AB=|﹣1﹣5|=6;
(3)AB与AC相等.理由:
∵AB==5;
AC==5;
BC=|3﹣(﹣3)|=6.
∴AB=AC.
37.解:(1)如图,过D作DE⊥x轴,垂足为E,过C作CF⊥x轴,垂足为F,
∴S四边形ABCD=S△ADE+S四边形DEFC+S△CFB
∵S△ADE=×1×4=2,
S四边形DEFC=(3+4)×1=,
S△CFB=×2×3=3,
∴S四边形ABCD=2++3=;
(2)由题可得,四边形ABCD先向左平移3个单位,再向下平移1个单位得四边形A′B′C′D',
∴平移后,各顶点的横坐标减小3,纵坐标减小1,
∵A(1,0)、B(5,0)、C(3,3),D(2,4),
∴A′(﹣2,﹣1),B′(2,﹣1),C′(0,2),D′(﹣1,3).
38.解:(1)当c=0时,a、b满足:a﹣2b=﹣1,2a﹣3b=﹣4,
解得a=﹣5,b=﹣2,
∴A点的坐标为(5,﹣5),B点的坐标为(﹣2,0);
(2)∠EDC=∠ABC+∠ACB.
证明:如图,延长BA至G,
由平移得,AB∥DE,
∴∠EDC=∠GAC,
又∵∠GAC是△ABC的外角,
∴∠GAC=∠ABC+∠ACB,
∴∠EDC=∠ABC+∠ACB;
(3)如图,∵坐标原点O与点A对应,且A(5,﹣5),
∴线段AB向上平移5个单位,再向左平移5个单位,可平移到OF处,
又∵F与B对应,且B(﹣2,0),
∴F点的横坐标为:﹣2﹣5=﹣7,纵坐标为:0+5=5,
∴F点的坐标为(﹣7,5).
39.解:(1)1﹣a=﹣3,a=4.
(2)由a=4得:2a﹣12=2×4﹣12=﹣4,又点Q(x,y)位于第二象限,所以y>0;
取y=1,得点Q的坐标为(﹣4,1).
(3)因为点P(2a﹣12,1﹣a)位于第三象限,
所以,
解得:1<a<6.
因为点P的横、纵坐标都是整数,所以a=2或3或4或5;
当a=2时,1﹣a=﹣1,所以PQ>1;
当a=3时,1﹣a=﹣2,所以PQ>2;
当a=4时,1﹣a=﹣3,所以PQ>3;
当a=5时,1﹣a=﹣4,所以PQ>4.
40.解:(1)∵点P的坐标为(x,y),若x=y,
∴点P在一、三象限内两坐标轴夹角的平分线上.
∵x+y=0,
∴x、y互为相反数,
∴P点在二、四象限内两坐标轴夹角的平分线上.
故答案为:在一、三象限内两坐标轴夹角的平分线上.在二、四象限内两坐标轴夹角的平分线上.
(2)∵点Q到两坐标轴的距离相等,
∴|2﹣2a|=|8+a|,
∴2﹣2a=8+a或2﹣2a=﹣8﹣a,
解得a=﹣2或a=10,
当a=﹣2时,2﹣2a=2﹣2×(﹣2)=6,8+a=8﹣2=6,
当a=10时,2﹣2a=2﹣20=﹣18,8+a=8+10=18,
所以,点Q的坐标为(6,6)或(﹣18,18).
41.解:(1)中秋节D(8,15),国庆节E(10,1).
(2)如图.
(3)将图形补成一个矩形AEFG
则:S长AEFG=9×14=126
S△DEF==14
S△ACH==8
S梯形CDGH=(4+7)×=55
S四AEDC=126﹣14﹣8﹣55=49
答:该图形的面积为49.
42.解:(1)把x=﹣2代入2x﹣y=﹣6,得
2×(﹣2)﹣y=﹣6,
解得y=2,
所以,点P坐标是(﹣2,2).
故答案是:(﹣2,2).
(2)∵2x﹣y=﹣6,
∴y=2x+6.
∵点P在第二象限,
∴得﹣3<x<0.
又∵x是整数
∴x=﹣1,﹣2.
当x=﹣1时,y=4;
当x=﹣2时,y=2.
(3)不存在.理由如下:
如图,
∵点P在第一象限,
作PQ⊥x轴,垂足为Q,则PQ=2x+6,
又∵OA=0﹣(﹣8)=8,
∴S=×OA×PQ=12,即×8×(2x+6)=12,得x=,此时点P的坐标为(,3).
∴点P不在第一象限,即不存在这样的点P.
43.解:(1)A(3,3),B(﹣2,﹣2),C(4,﹣3);
(2)如图所示:
S△ABC=S矩形DECF﹣S△BEC﹣S△ADB﹣S△AFC
==.
44.解:(1)∵C(﹣1,﹣3),
∴|﹣3|=3,
∴点C到x轴的距离为3;
(2)∵A(﹣2,3)、B(4,3)、C(﹣1,﹣3)
∴AB=4﹣(﹣2)=6,点C到边AB的距离为:3﹣(﹣3)=6,
∴△ABC的面积为:6×6÷2=18.
(3)设点P的坐标为(0,y),
∵△ABP的面积为6,A(﹣2,3)、B(4,3),
∴6×|y﹣3|=6,
∴|y﹣3|=2,
∴y=1或y=5,
∴P点的坐标为(0,1)或(0,5).
45.解:(1)如图所示.
(2)过B作BE⊥AD于E,过C作CF⊥AD于F,则
S四边形ABCD=S△ABE+S梯形BEFC+S△CFD
=
=
=9+21+8
=38
答:四边形ABCD的面积为38.
46.解:(1)如图:直角坐标系即为所求;
(2)存在点C,使△ABC为等腰三角形,如图,
∵AB==5,
∵以AB为腰,
∴AC4=BC4,舍去,
∴所有满足条件的点C的坐标为C(7,0)或C′(4,0)或C″(﹣6,0).
同课章节目录
