苏科版数学 九年级上 25.1锐角三角函数(第一课时)
文档属性
| 名称 | 苏科版数学 九年级上 25.1锐角三角函数(第一课时) |
|
|
| 格式 | zip | ||
| 文件大小 | 22.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-24 07:02:09 | ||
图片预览


文档简介
24.1锐角的三角函数
教学目标
1.知识与技能.
理解锐角三角函数中的正弦的概念,并能够举例说明.
2.过程与方法.
经历探索正弦概念的过程,掌握运用tanA表示坡度.
3.情感、态度与价值观.
培养良好的数形结合的能力,体会三角函数在现实生活中的应用价值.
重难点、关键
1.重点:理解正切的概念.
2.难点:怎样运用已学过的函数概念来理解正切.
3.关键:要注意函数的定义,把握应用的方法.
教学准备
1.教师准备:投影仪、制作投影片.
2.学生准备:复习上一节课内容,预习本节课内容.
教学过程
创设情境
(课件展示汽车爬坡图)
师:汽车的爬坡能力是衡量汽车的性能的重要指标之一。怎样描述坡面的倾斜程度——坡度呢?
生:稍作思考讨论、交流。
交流
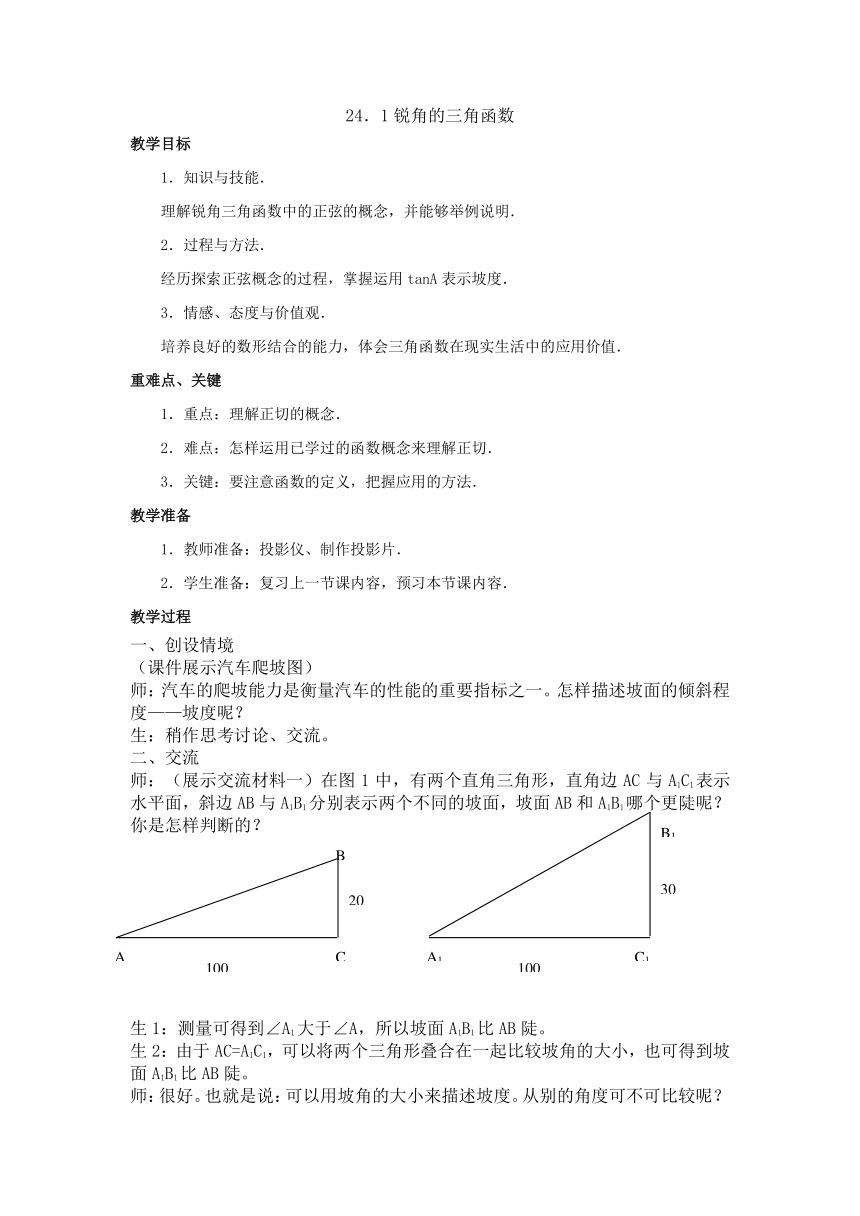
师:(展示交流材料一)在图1中,有两个直角三角形,直角边AC与A1C1表示水平面,斜边AB与A1B1分别表示两个不同的坡面,坡面AB和A1B1哪个更陡呢?你是怎样判断的?
生1:测量可得到∠A1大于∠A,所以坡面A1B1比AB陡。
生2:由于AC=A1C1,可以将两个三角形叠合在一起比较坡角的大小,也可得到坡面A1B1比AB陡。
师:很好。也就是说:可以用坡角的大小来描述坡度。从别的角度可不可比较呢?
生3:通过计算两直角边的比,0.2<0.3,所以坡面A1B1比AB陡。
师:(面露惊赞之色)在家同意吗 很好,完全可行.
用这两种方法不妨再试下面的坡面的比较.
交流材料二:
(略).
师:用坡角的大小和它的对边与邻边之比都能描述坡度的大小,那么这个角和比值之间会不会存在某种联系呢?
课件出示:交流材料三
在锐角A的一边上任取一点B,自点B向另一边作垂线,垂足为C,得Rt△ABC,再任取一点B1,自点B1向另一边作垂线,垂足为C1,得Rt△AB1C1,、、、、、、,这样我们可以得到无数个直角三角形。
师:显然,这些直角三角形中锐角A是相等的,也就是确定的,那么这些直角三角形中锐角A的对边与、 、、、、、、、邻边之比有何关系呢?
生:相等。
师:为什么?
生:因为这些直角三角形相似,对应边成比例。(写出推导过程)
师:通过以上分析,我们发现了直角三角形中一个锐角A和其对边与邻边之比有一定联系,请说说这个联系是什么?
生:(充分思考,多人表述,直至准确、全面)在Rt△ABC,当锐角∠A的大小确定后,无论直角三角形的大小怎样变化,∠A的对边与邻边的比值总是一个固定值,总是唯一值。
正切的定义
正是由于在Rt△ABC,当锐角∠A的大小确定后,无论直角三角形的大小怎样变化,∠A的对边与邻边的比值总是一个固定值,总是唯一值,这个比值才值得关注,才有如下定义:
在Rt△ABC,把锐角∠A的对边与邻边的比值叫做∠A的正切,记作,即tanA=
.
坡度与坡角
师:如图24-6,正切经常用来描述坡面的坡度。坡面的铅直高度h与水平长度l的比叫做坡面的坡度(或坡比),记作,即
i=
坡面与水平面的夹角叫做坡角(或称倾斜角),记作a,
师:你能发现坡度与坡角的关系吗?
生:思考后回答。
师生:i=tana
师:由此关系坡度随坡角的变化如何变化?
引导学生:坡度越大,越角a越大,坡面越陡。
对正切的深层认识
师:tanA还是∠A吗
生:不是. ∠A是一个角,tanA指的是以∠A为锐角的直角三角形中∠A的对边与邻边的比,是一个值.
师:非常准确.
师:同学们还记得函数的概念吗
生:一般地,设一个变化过程中有两个变量x,y,如果对于x在它允许取值范围内的每一个值,y都有唯一确定的值与它对应,那么就说x是自变量,y是x的函数.
师:在直角三角形中,直角三角形有许许多多,是变化的,当然它的一个锐角∠A和tanA是两个变量.由以上分析可知当∠A在其允许取值范围内的每一个确定的值,tanA的值是否唯一确定呢
生:唯一确定.
师:可见tanA与∠A是什么关系呢
生:(豁然开朗)函数关系.
师:因而我们把tanA叫做锐角∠A的正切函数.
正切的应用
师:有了正切这个概念后,我们会不会重新来描述坡度呢?
生:可以用正切来描述坡度。
师:对。坡面的铅直高度h和水平长度l的比叫坡度,记做i,即i=坡面与水平面的夹角叫坡角,记做,于是i=。显然,坡角越大,坡度越大,坡越陡.
例题
例1如图24-7,在Rt⊿ABC中,∠C=900,AC=4,BC=3.
求tanA和tanB.
师:同学们先自己做做看。巡视。
生:试解。
师生:
解:tanA=tanB=.
课堂小结
生:自己小结表达。
师生补充完善:本节课主要学习了正切函数的定义及坡度的描述。
课堂练习P102 1.
作业P102 2.
教学反思:
A1
B1
C1
30
100
C
A
B
100
20
A1
B1
C1
30
100
C
A
B
100
20
C
A
B
C1
B1
B2
C2
C
A
B
b
a
I=h:l
a
图24-6
l
h
A
B
C
3
图24-7
4
教学目标
1.知识与技能.
理解锐角三角函数中的正弦的概念,并能够举例说明.
2.过程与方法.
经历探索正弦概念的过程,掌握运用tanA表示坡度.
3.情感、态度与价值观.
培养良好的数形结合的能力,体会三角函数在现实生活中的应用价值.
重难点、关键
1.重点:理解正切的概念.
2.难点:怎样运用已学过的函数概念来理解正切.
3.关键:要注意函数的定义,把握应用的方法.
教学准备
1.教师准备:投影仪、制作投影片.
2.学生准备:复习上一节课内容,预习本节课内容.
教学过程
创设情境
(课件展示汽车爬坡图)
师:汽车的爬坡能力是衡量汽车的性能的重要指标之一。怎样描述坡面的倾斜程度——坡度呢?
生:稍作思考讨论、交流。
交流
师:(展示交流材料一)在图1中,有两个直角三角形,直角边AC与A1C1表示水平面,斜边AB与A1B1分别表示两个不同的坡面,坡面AB和A1B1哪个更陡呢?你是怎样判断的?
生1:测量可得到∠A1大于∠A,所以坡面A1B1比AB陡。
生2:由于AC=A1C1,可以将两个三角形叠合在一起比较坡角的大小,也可得到坡面A1B1比AB陡。
师:很好。也就是说:可以用坡角的大小来描述坡度。从别的角度可不可比较呢?
生3:通过计算两直角边的比,0.2<0.3,所以坡面A1B1比AB陡。
师:(面露惊赞之色)在家同意吗 很好,完全可行.
用这两种方法不妨再试下面的坡面的比较.
交流材料二:
(略).
师:用坡角的大小和它的对边与邻边之比都能描述坡度的大小,那么这个角和比值之间会不会存在某种联系呢?
课件出示:交流材料三
在锐角A的一边上任取一点B,自点B向另一边作垂线,垂足为C,得Rt△ABC,再任取一点B1,自点B1向另一边作垂线,垂足为C1,得Rt△AB1C1,、、、、、、,这样我们可以得到无数个直角三角形。
师:显然,这些直角三角形中锐角A是相等的,也就是确定的,那么这些直角三角形中锐角A的对边与、 、、、、、、、邻边之比有何关系呢?
生:相等。
师:为什么?
生:因为这些直角三角形相似,对应边成比例。(写出推导过程)
师:通过以上分析,我们发现了直角三角形中一个锐角A和其对边与邻边之比有一定联系,请说说这个联系是什么?
生:(充分思考,多人表述,直至准确、全面)在Rt△ABC,当锐角∠A的大小确定后,无论直角三角形的大小怎样变化,∠A的对边与邻边的比值总是一个固定值,总是唯一值。
正切的定义
正是由于在Rt△ABC,当锐角∠A的大小确定后,无论直角三角形的大小怎样变化,∠A的对边与邻边的比值总是一个固定值,总是唯一值,这个比值才值得关注,才有如下定义:
在Rt△ABC,把锐角∠A的对边与邻边的比值叫做∠A的正切,记作,即tanA=
.
坡度与坡角
师:如图24-6,正切经常用来描述坡面的坡度。坡面的铅直高度h与水平长度l的比叫做坡面的坡度(或坡比),记作,即
i=
坡面与水平面的夹角叫做坡角(或称倾斜角),记作a,
师:你能发现坡度与坡角的关系吗?
生:思考后回答。
师生:i=tana
师:由此关系坡度随坡角的变化如何变化?
引导学生:坡度越大,越角a越大,坡面越陡。
对正切的深层认识
师:tanA还是∠A吗
生:不是. ∠A是一个角,tanA指的是以∠A为锐角的直角三角形中∠A的对边与邻边的比,是一个值.
师:非常准确.
师:同学们还记得函数的概念吗
生:一般地,设一个变化过程中有两个变量x,y,如果对于x在它允许取值范围内的每一个值,y都有唯一确定的值与它对应,那么就说x是自变量,y是x的函数.
师:在直角三角形中,直角三角形有许许多多,是变化的,当然它的一个锐角∠A和tanA是两个变量.由以上分析可知当∠A在其允许取值范围内的每一个确定的值,tanA的值是否唯一确定呢
生:唯一确定.
师:可见tanA与∠A是什么关系呢
生:(豁然开朗)函数关系.
师:因而我们把tanA叫做锐角∠A的正切函数.
正切的应用
师:有了正切这个概念后,我们会不会重新来描述坡度呢?
生:可以用正切来描述坡度。
师:对。坡面的铅直高度h和水平长度l的比叫坡度,记做i,即i=坡面与水平面的夹角叫坡角,记做,于是i=。显然,坡角越大,坡度越大,坡越陡.
例题
例1如图24-7,在Rt⊿ABC中,∠C=900,AC=4,BC=3.
求tanA和tanB.
师:同学们先自己做做看。巡视。
生:试解。
师生:
解:tanA=tanB=.
课堂小结
生:自己小结表达。
师生补充完善:本节课主要学习了正切函数的定义及坡度的描述。
课堂练习P102 1.
作业P102 2.
教学反思:
A1
B1
C1
30
100
C
A
B
100
20
A1
B1
C1
30
100
C
A
B
100
20
C
A
B
C1
B1
B2
C2
C
A
B
b
a
I=h:l
a
图24-6
l
h
A
B
C
3
图24-7
4
