7.4 认识三角形 高频易错题汇编(含解析)
文档属性
| 名称 | 7.4 认识三角形 高频易错题汇编(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 225.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-20 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
7.4 认识三角形 高频易错题汇编
一、选择题(共10小题)
1.下列图形中有稳定性的是( )
A.正方形 B.长方形 C.直角三角形 D.平行四边形
2.已知锐角三角形的边长是2,3,x,那么第三边x的取值范围是( )
A.1<x< B. C. D.
3.如图是一个由四根木条钉成的框架,拉动其中两根木条后,它的形状将会改变,若固定其形状,下列有四种加固木条的方法,不能固定形状的是钉在( )两点上的木条.
A.A、F B.C、E C.C、A D.E、F
4.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A. B. C. D.
5.如图,AD是△ABC的中线,已知△ABD的周长为25cm,AB比AC长6cm,则△ACD的周长为( )
A.19cm B.22cm C.25cm D.31cm
6.如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3 C.6 D.不能确定
7.若一个三角形的三条边长分别为3,2a﹣1,6,则整数a的值可能是( )
A.2,3 B.3,4 C.2,3,4 D.3,4,5
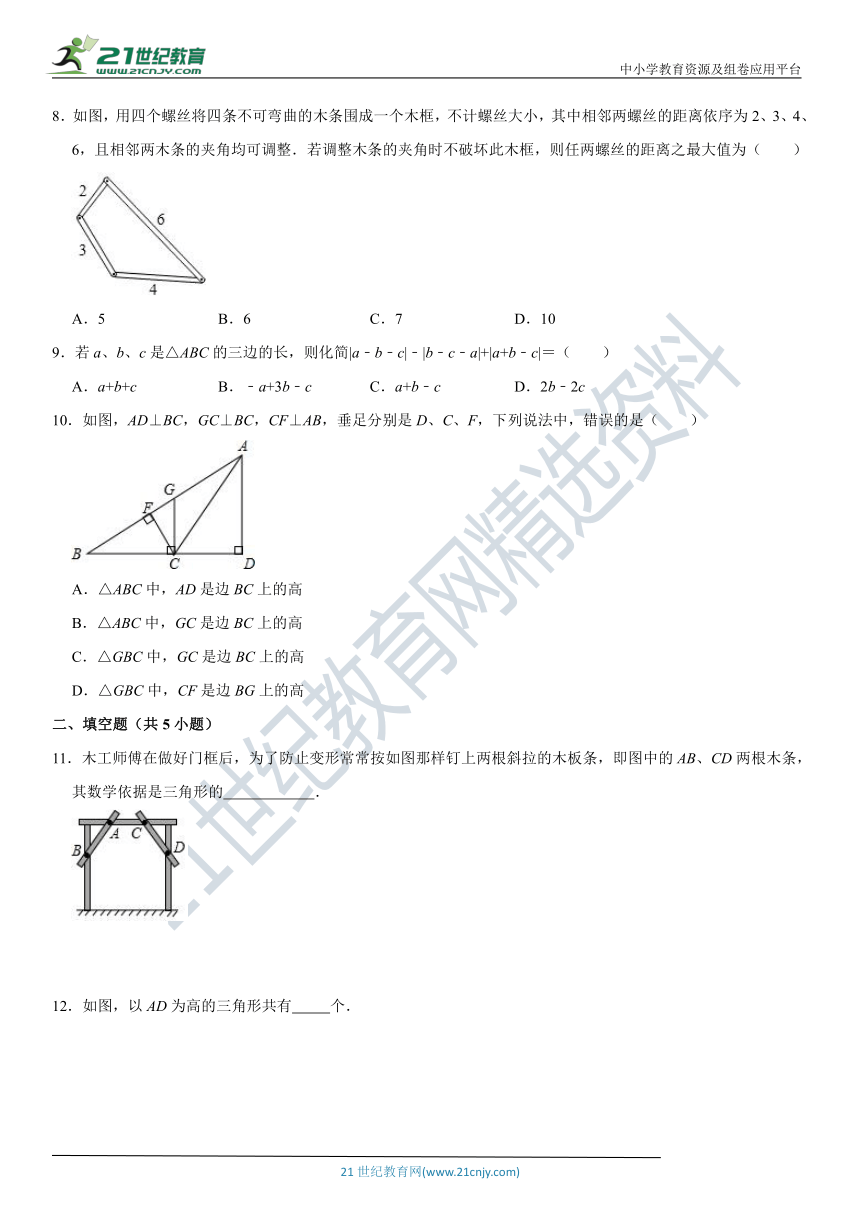
8.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为( )
A.5 B.6 C.7 D.10
9.若a、b、c是△ABC的三边的长,则化简|a﹣b﹣c|﹣|b﹣c﹣a|+|a+b﹣c|=( )
A.a+b+c B.﹣a+3b﹣c C.a+b﹣c D.2b﹣2c
10.如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,错误的是( )
A.△ABC中,AD是边BC上的高
B.△ABC中,GC是边BC上的高
C.△GBC中,GC是边BC上的高
D.△GBC中,CF是边BG上的高
二、填空题(共5小题)
11.木工师傅在做好门框后,为了防止变形常常按如图那样钉上两根斜拉的木板条,即图中的AB、CD两根木条,其数学依据是三角形的 .
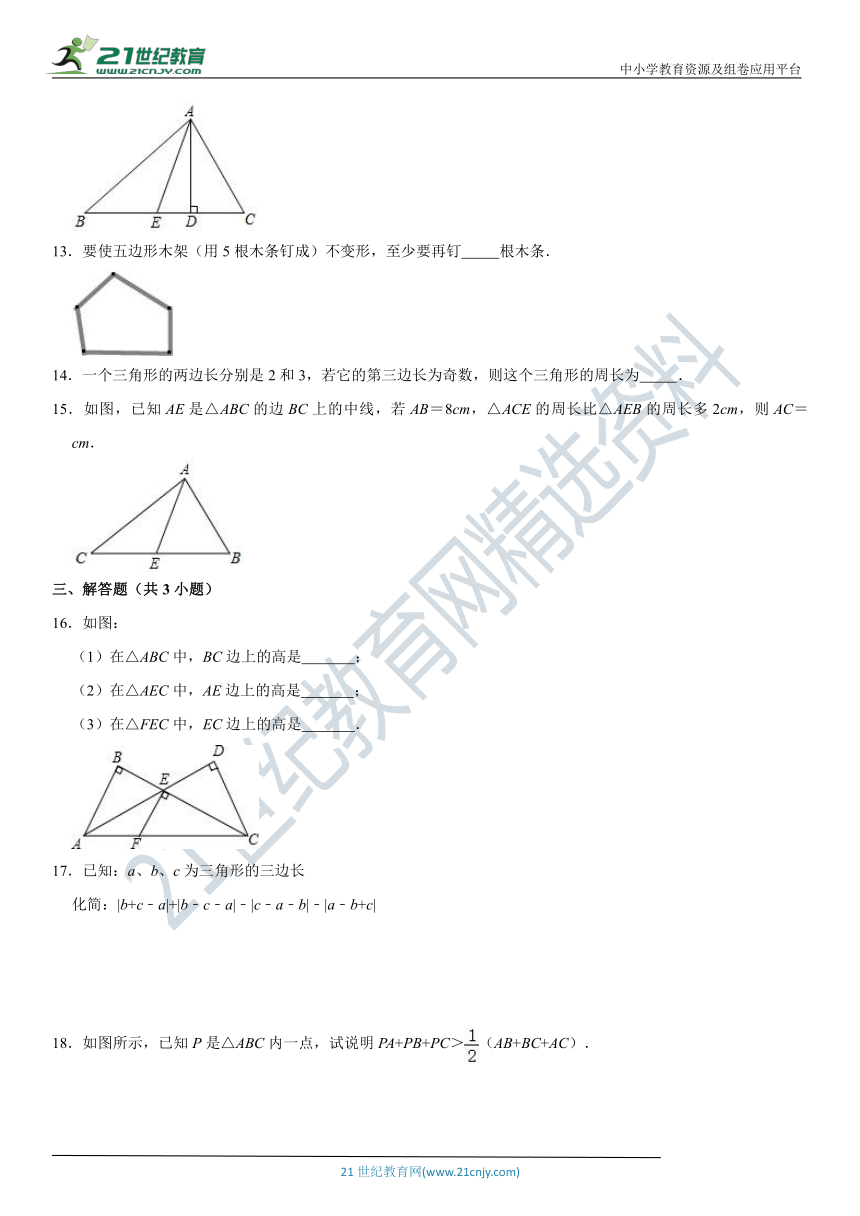
12.如图,以AD为高的三角形共有 个.
13.要使五边形木架(用5根木条钉成)不变形,至少要再钉 根木条.
14.一个三角形的两边长分别是2和3,若它的第三边长为奇数,则这个三角形的周长为 .
15.如图,已知AE是△ABC的边BC上的中线,若AB=8cm,△ACE的周长比△AEB的周长多2cm,则AC= cm.
三、解答题(共3小题)
16.如图:
(1)在△ABC中,BC边上的高是 ;
(2)在△AEC中,AE边上的高是 ;
(3)在△FEC中,EC边上的高是 .
17.已知:a、b、c为三角形的三边长
化简:|b+c﹣a|+|b﹣c﹣a|﹣|c﹣a﹣b|﹣|a﹣b+c|
18.如图所示,已知P是△ABC内一点,试说明PA+PB+PC>(AB+BC+AC).
试题解析
一、选择题(共10小题)
1.解:根据三角形具有稳定性,可得四个选项中只有直角三角形具有稳定性.
答案:C.
2.解:首先要能组成三角形,易得 1<x<5
下面求该三角形为直角三角形的边长情况(此为临界情况),显然长度为2的边对应的角必为锐角(2<3,短边对小角)则只要考虑3或者x为斜边的情况.
3为斜边时,由勾股定理,22+x2=32,得x=√5 作出图形,固定2边,旋转3边易知当1<x<√5 时,该三角形是以3为最大边的钝角三角形;
x 为斜边时,由勾股定理,22+32=x2,得x=√13,同样作图可得 当√13<x<5时,该三角形是以x为最大边的钝角三角形.
综上可知,当√5<x<√13 时,原三角形为锐角三角形.
答案:B.
3.解:A、A、F与D能够组三角形,能固定形状,故本选项错误;
B、C、E与B能够组三角形,能固定形状,故本选项错误;
C、C、A与B能够组三角形,能固定形状,故本选项错误;
D、E、F不能与A、B、C、D中的任意点构成三角形,不能固定形状,故本选项正确.
答案:D.
4.解:为△ABC中BC边上的高的是A选项.
答案:A.
5.解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)﹣(AC+AD+CD)=AB﹣AC,
∵△ABD的周长为25cm,AB比AC长6cm,
∴△ACD周长为:25﹣6=19cm.
答案:A.
6.解:∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长的差是:(AB+BD+AD)﹣(BC+BD+CD)=AB﹣BC=5﹣3=2.
答案:A.
7.解:∵一个三角形的三条边长分别为3,2a﹣1,6,
∴,
解得:2<a<5,
故整数a的值可能是:3,4.
答案:B.
8.解:已知4条木棍的四边长为2、3、4、6;
①选2+3、4、6作为三角形,则三边长为5、4、6;5﹣4<6<5+4,能构成三角形,此时两个螺丝间的最长距离为6;
②选3+4、6、2作为三角形,则三边长为2、7、6;6﹣2<7<6+2,能构成三角形,此时两个螺丝间的最大距离为7;
③选4+6、2、3作为三角形,则三边长为10、2、3;2+3<10,不能构成三角形,此种情况不成立;
④选6+2、3、4作为三角形,则三边长为8、3、4;而3+4<8,不能构成三角形,此种情况不成立;
综上所述,任两螺丝的距离之最大值为7.
答案:C.
9.解:|a﹣b﹣c|﹣|b﹣c﹣a|+|a+b﹣c|,
=﹣a+b+c﹣(﹣b+c+a)+(a+b﹣c),
=﹣a+b+c+b﹣c﹣a+a+b﹣c,
=﹣a+3b﹣c,
答案:B.
10.解:A、∵AD⊥BC,
∴△ABC中,AD是边BC上的高正确,故本选项错误;
B、AD是△ABC的边BC上的高,GC不是,故本选项正确;
C、∵GC⊥BC,
∴△GBC中,GC是边BC上的高正确,故本选项错误;
D、∵CF⊥AB,
∴△GBC中,CF是边BG上的高正确,故本选项错误.
答案:B.
二、填空题(共5小题)
11.解:结合图形,为防止变形钉上两条斜拉的木板条,构成了三角形,所以这样做根据的数学道理是三角形的稳定性.
答案:三角形的稳定性.
12.解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
答案:6
13.解:再钉上两根木条,就可以使五边形分成三个三角形.故至少要再钉两根木条.
14.解:设第三边长为x,
∵两边长分别是2和3,
∴3﹣2<x<3+2,
即:1<x<5,
∵第三边长为奇数,
∴x=3,
∴这个三角形的周长为2+3+3=8,
答案:8.
15.解:∵AE是△ABC的边BC上的中线,
∴CE=BE,
又∵AE=AE,△ACE的周长比△AEB的周长多2cm,
∴AC﹣AB=2cm,
即AC﹣8=2cm,
∴AC=10cm,
答案:10;
三、解答题(共3小题)
16.解:(1)在△ABC中,BC边上的高是AB;
(2)在△AEC中,AE边上的高是DC;
(3)在△FEC中,EC边上的高是EF;
答案:AB,DC,EF.
17.解:∵a、b、c为三角形三边的长,
∴a+b>c,a+c>b,b+c>a,
∴原式=|(b+c)﹣a|+|b﹣(c+a)|﹣|c﹣(a+b)|﹣|(a+c)﹣b|
=b+c﹣a+a+c﹣b﹣a﹣b+c+b﹣a﹣c
=2c﹣2a.
18.证明:在△ABP中:AP+BP>AB.
同理:BP+PC>BC,AP+PC>AC.
以上三式分别相加得到:
2(PA+PB+PC)>AB+BC+AC,
即PA+PB+PC>(AB+BC+AC).
_21?????????è?????(www.21cnjy.com)_
7.4 认识三角形 高频易错题汇编
一、选择题(共10小题)
1.下列图形中有稳定性的是( )
A.正方形 B.长方形 C.直角三角形 D.平行四边形
2.已知锐角三角形的边长是2,3,x,那么第三边x的取值范围是( )
A.1<x< B. C. D.
3.如图是一个由四根木条钉成的框架,拉动其中两根木条后,它的形状将会改变,若固定其形状,下列有四种加固木条的方法,不能固定形状的是钉在( )两点上的木条.
A.A、F B.C、E C.C、A D.E、F
4.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A. B. C. D.
5.如图,AD是△ABC的中线,已知△ABD的周长为25cm,AB比AC长6cm,则△ACD的周长为( )
A.19cm B.22cm C.25cm D.31cm
6.如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3 C.6 D.不能确定
7.若一个三角形的三条边长分别为3,2a﹣1,6,则整数a的值可能是( )
A.2,3 B.3,4 C.2,3,4 D.3,4,5
8.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为( )
A.5 B.6 C.7 D.10
9.若a、b、c是△ABC的三边的长,则化简|a﹣b﹣c|﹣|b﹣c﹣a|+|a+b﹣c|=( )
A.a+b+c B.﹣a+3b﹣c C.a+b﹣c D.2b﹣2c
10.如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,错误的是( )
A.△ABC中,AD是边BC上的高
B.△ABC中,GC是边BC上的高
C.△GBC中,GC是边BC上的高
D.△GBC中,CF是边BG上的高
二、填空题(共5小题)
11.木工师傅在做好门框后,为了防止变形常常按如图那样钉上两根斜拉的木板条,即图中的AB、CD两根木条,其数学依据是三角形的 .
12.如图,以AD为高的三角形共有 个.
13.要使五边形木架(用5根木条钉成)不变形,至少要再钉 根木条.
14.一个三角形的两边长分别是2和3,若它的第三边长为奇数,则这个三角形的周长为 .
15.如图,已知AE是△ABC的边BC上的中线,若AB=8cm,△ACE的周长比△AEB的周长多2cm,则AC= cm.
三、解答题(共3小题)
16.如图:
(1)在△ABC中,BC边上的高是 ;
(2)在△AEC中,AE边上的高是 ;
(3)在△FEC中,EC边上的高是 .
17.已知:a、b、c为三角形的三边长
化简:|b+c﹣a|+|b﹣c﹣a|﹣|c﹣a﹣b|﹣|a﹣b+c|
18.如图所示,已知P是△ABC内一点,试说明PA+PB+PC>(AB+BC+AC).
试题解析
一、选择题(共10小题)
1.解:根据三角形具有稳定性,可得四个选项中只有直角三角形具有稳定性.
答案:C.
2.解:首先要能组成三角形,易得 1<x<5
下面求该三角形为直角三角形的边长情况(此为临界情况),显然长度为2的边对应的角必为锐角(2<3,短边对小角)则只要考虑3或者x为斜边的情况.
3为斜边时,由勾股定理,22+x2=32,得x=√5 作出图形,固定2边,旋转3边易知当1<x<√5 时,该三角形是以3为最大边的钝角三角形;
x 为斜边时,由勾股定理,22+32=x2,得x=√13,同样作图可得 当√13<x<5时,该三角形是以x为最大边的钝角三角形.
综上可知,当√5<x<√13 时,原三角形为锐角三角形.
答案:B.
3.解:A、A、F与D能够组三角形,能固定形状,故本选项错误;
B、C、E与B能够组三角形,能固定形状,故本选项错误;
C、C、A与B能够组三角形,能固定形状,故本选项错误;
D、E、F不能与A、B、C、D中的任意点构成三角形,不能固定形状,故本选项正确.
答案:D.
4.解:为△ABC中BC边上的高的是A选项.
答案:A.
5.解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)﹣(AC+AD+CD)=AB﹣AC,
∵△ABD的周长为25cm,AB比AC长6cm,
∴△ACD周长为:25﹣6=19cm.
答案:A.
6.解:∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长的差是:(AB+BD+AD)﹣(BC+BD+CD)=AB﹣BC=5﹣3=2.
答案:A.
7.解:∵一个三角形的三条边长分别为3,2a﹣1,6,
∴,
解得:2<a<5,
故整数a的值可能是:3,4.
答案:B.
8.解:已知4条木棍的四边长为2、3、4、6;
①选2+3、4、6作为三角形,则三边长为5、4、6;5﹣4<6<5+4,能构成三角形,此时两个螺丝间的最长距离为6;
②选3+4、6、2作为三角形,则三边长为2、7、6;6﹣2<7<6+2,能构成三角形,此时两个螺丝间的最大距离为7;
③选4+6、2、3作为三角形,则三边长为10、2、3;2+3<10,不能构成三角形,此种情况不成立;
④选6+2、3、4作为三角形,则三边长为8、3、4;而3+4<8,不能构成三角形,此种情况不成立;
综上所述,任两螺丝的距离之最大值为7.
答案:C.
9.解:|a﹣b﹣c|﹣|b﹣c﹣a|+|a+b﹣c|,
=﹣a+b+c﹣(﹣b+c+a)+(a+b﹣c),
=﹣a+b+c+b﹣c﹣a+a+b﹣c,
=﹣a+3b﹣c,
答案:B.
10.解:A、∵AD⊥BC,
∴△ABC中,AD是边BC上的高正确,故本选项错误;
B、AD是△ABC的边BC上的高,GC不是,故本选项正确;
C、∵GC⊥BC,
∴△GBC中,GC是边BC上的高正确,故本选项错误;
D、∵CF⊥AB,
∴△GBC中,CF是边BG上的高正确,故本选项错误.
答案:B.
二、填空题(共5小题)
11.解:结合图形,为防止变形钉上两条斜拉的木板条,构成了三角形,所以这样做根据的数学道理是三角形的稳定性.
答案:三角形的稳定性.
12.解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
答案:6
13.解:再钉上两根木条,就可以使五边形分成三个三角形.故至少要再钉两根木条.
14.解:设第三边长为x,
∵两边长分别是2和3,
∴3﹣2<x<3+2,
即:1<x<5,
∵第三边长为奇数,
∴x=3,
∴这个三角形的周长为2+3+3=8,
答案:8.
15.解:∵AE是△ABC的边BC上的中线,
∴CE=BE,
又∵AE=AE,△ACE的周长比△AEB的周长多2cm,
∴AC﹣AB=2cm,
即AC﹣8=2cm,
∴AC=10cm,
答案:10;
三、解答题(共3小题)
16.解:(1)在△ABC中,BC边上的高是AB;
(2)在△AEC中,AE边上的高是DC;
(3)在△FEC中,EC边上的高是EF;
答案:AB,DC,EF.
17.解:∵a、b、c为三角形三边的长,
∴a+b>c,a+c>b,b+c>a,
∴原式=|(b+c)﹣a|+|b﹣(c+a)|﹣|c﹣(a+b)|﹣|(a+c)﹣b|
=b+c﹣a+a+c﹣b﹣a﹣b+c+b﹣a﹣c
=2c﹣2a.
18.证明:在△ABP中:AP+BP>AB.
同理:BP+PC>BC,AP+PC>AC.
以上三式分别相加得到:
2(PA+PB+PC)>AB+BC+AC,
即PA+PB+PC>(AB+BC+AC).
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
