导数计算
图片预览





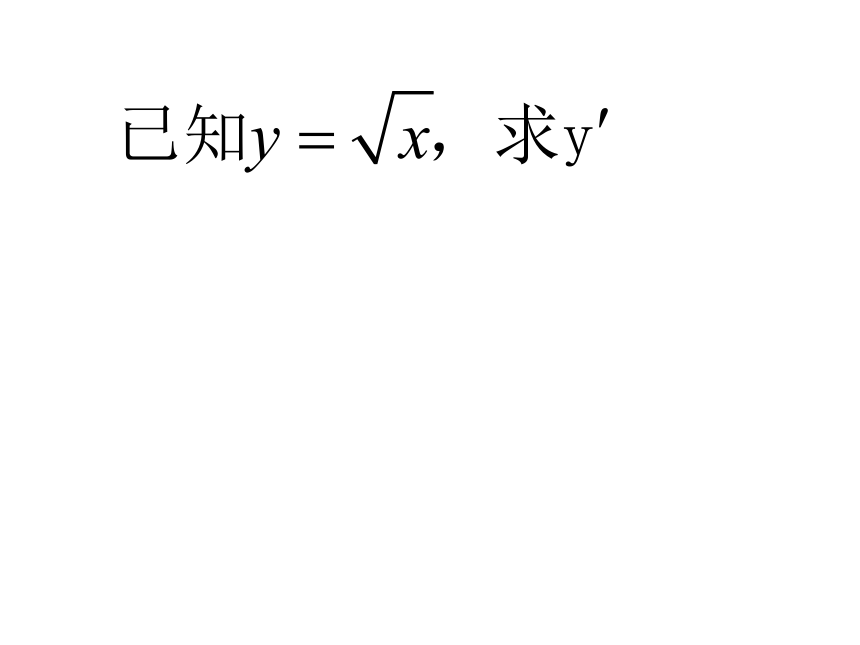

文档简介
(共22张PPT)
导数的计算
知识回顾
2.求函数的导数的方法是:
1.导数的定义
叫函数在x=x0的导数
函数f(x)在点x0处的导数 就是导函数 在x=
x0处的函数值,即 .这也是求函数在点x0
处的导数的方法之一。
3.函数 y=f(x)在点x0处的导数的几何意义,就是曲线y=
f(x)在点P(x0 ,f(x0))处的切线的斜率.
4.求切线方程的步骤:
(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。
(2)根据直线方程的点斜式写出切线方程,即
新课——几种常见函数的导数
根据导数的定义可以得出一些常见函数的导数公式.
公式1: .
1) 函数y=f(x)=c的导数.
求下列函数的导数:
请注意公式中的条件是 ,但根据我们所掌握的知识,只能就 的情况加以证明.这个公式称为幂函数的导数公式.事实上n可以是任意实数.
思考 .
思考
我们今后可以直接使用的
基本初等函数的导数公式
典型例题
解:由基本初等函数导数公式得:
P/(t)=1.05tln1.05
P/ (10)=1.0510ln1.05≈0.08(年)
所以,在第10个年头,这种商品的
价格约以0.08元/年的速度上涨.
例 求曲线y=sinx在点A(π/6,1/2)的切线方程
例 .已知P(-1,1),Q(2,4)是曲线y=x2上的两点,求与直线PQ平行的曲线y=x2的切线方程。
我们今后可以直接使用的
基本初等函数的导数公式
解:
法二:
法一:
例 : 已知曲线 在点P(1,1)处的切线与直线m平行且
距离等于 ,求直线m的方程.
设直线m的方程为3x+y+b=0,由平行线间的距离公式得:
故所求的直线m的方程为3x+y+6=0或3x+y-14=0.
练习:若直线y=3x+1是曲线y=ax3的切线,试求a的值.
解:设直线y=3x+1与曲线y=ax3相切于点P(x0,y0),则有:
y0=3x0+1①,y0=ax03②,3ax02=3.③
由①,②得3x0+1=ax03,由③得ax02=1,代入上式可得:
3x0+1=x0,x0=-1/2.
所以a (-1/2)3=1,a=4.
导数的计算
知识回顾
2.求函数的导数的方法是:
1.导数的定义
叫函数在x=x0的导数
函数f(x)在点x0处的导数 就是导函数 在x=
x0处的函数值,即 .这也是求函数在点x0
处的导数的方法之一。
3.函数 y=f(x)在点x0处的导数的几何意义,就是曲线y=
f(x)在点P(x0 ,f(x0))处的切线的斜率.
4.求切线方程的步骤:
(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。
(2)根据直线方程的点斜式写出切线方程,即
新课——几种常见函数的导数
根据导数的定义可以得出一些常见函数的导数公式.
公式1: .
1) 函数y=f(x)=c的导数.
求下列函数的导数:
请注意公式中的条件是 ,但根据我们所掌握的知识,只能就 的情况加以证明.这个公式称为幂函数的导数公式.事实上n可以是任意实数.
思考 .
思考
我们今后可以直接使用的
基本初等函数的导数公式
典型例题
解:由基本初等函数导数公式得:
P/(t)=1.05tln1.05
P/ (10)=1.0510ln1.05≈0.08(年)
所以,在第10个年头,这种商品的
价格约以0.08元/年的速度上涨.
例 求曲线y=sinx在点A(π/6,1/2)的切线方程
例 .已知P(-1,1),Q(2,4)是曲线y=x2上的两点,求与直线PQ平行的曲线y=x2的切线方程。
我们今后可以直接使用的
基本初等函数的导数公式
解:
法二:
法一:
例 : 已知曲线 在点P(1,1)处的切线与直线m平行且
距离等于 ,求直线m的方程.
设直线m的方程为3x+y+b=0,由平行线间的距离公式得:
故所求的直线m的方程为3x+y+6=0或3x+y-14=0.
练习:若直线y=3x+1是曲线y=ax3的切线,试求a的值.
解:设直线y=3x+1与曲线y=ax3相切于点P(x0,y0),则有:
y0=3x0+1①,y0=ax03②,3ax02=3.③
由①,②得3x0+1=ax03,由③得ax02=1,代入上式可得:
3x0+1=x0,x0=-1/2.
所以a (-1/2)3=1,a=4.
