2020-2021学年沪教新版七年级下册数学期末练习试题(Word版解析版)
文档属性
| 名称 | 2020-2021学年沪教新版七年级下册数学期末练习试题(Word版解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 311.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-21 10:28:42 | ||
图片预览



文档简介
2020-2021学年沪教新版七年级下册数学期末练习试题
一.选择题(共6小题,满分18分,每小题3分)
1.下列各数中,无理数是( )
A.
B.0
C.
D.
2.下列各式计算正确的是( )
A.×=6
B.÷=2
C.()2=9
D.(3)2=6
3.如图,已知a∥b,一块含30°角的直角三角板,如图所示放置,∠2=30°,则∠1等于( )
A.110°
B.130°
C.150°
D.160°
4.一个三角形的两边长为2和6,第三边为偶数.则这个三角形的周长为( )
A.16
B.14
C.12
D.10
5.若xy>0,则关于点P(x,y)的说法正确的是( )
A.在一或二象限
B.在一或四象限
C.在二或四象限
D.在一或三象限
6.给定下列条件,不能判定三角形是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3
B.∠A﹣∠C=∠B
C.∠A=∠B=2∠C
D.∠A=∠B=∠C
二.填空题(共12小题,满分24分,每小题2分)
7.如果某数的一个平方根是﹣5,那么这个数是
.
8.比较大小:﹣
﹣1.5.
9.将306
070
000用科学记数法表示并保留4个有效数字为
.
10.把化成幂的形式是
.
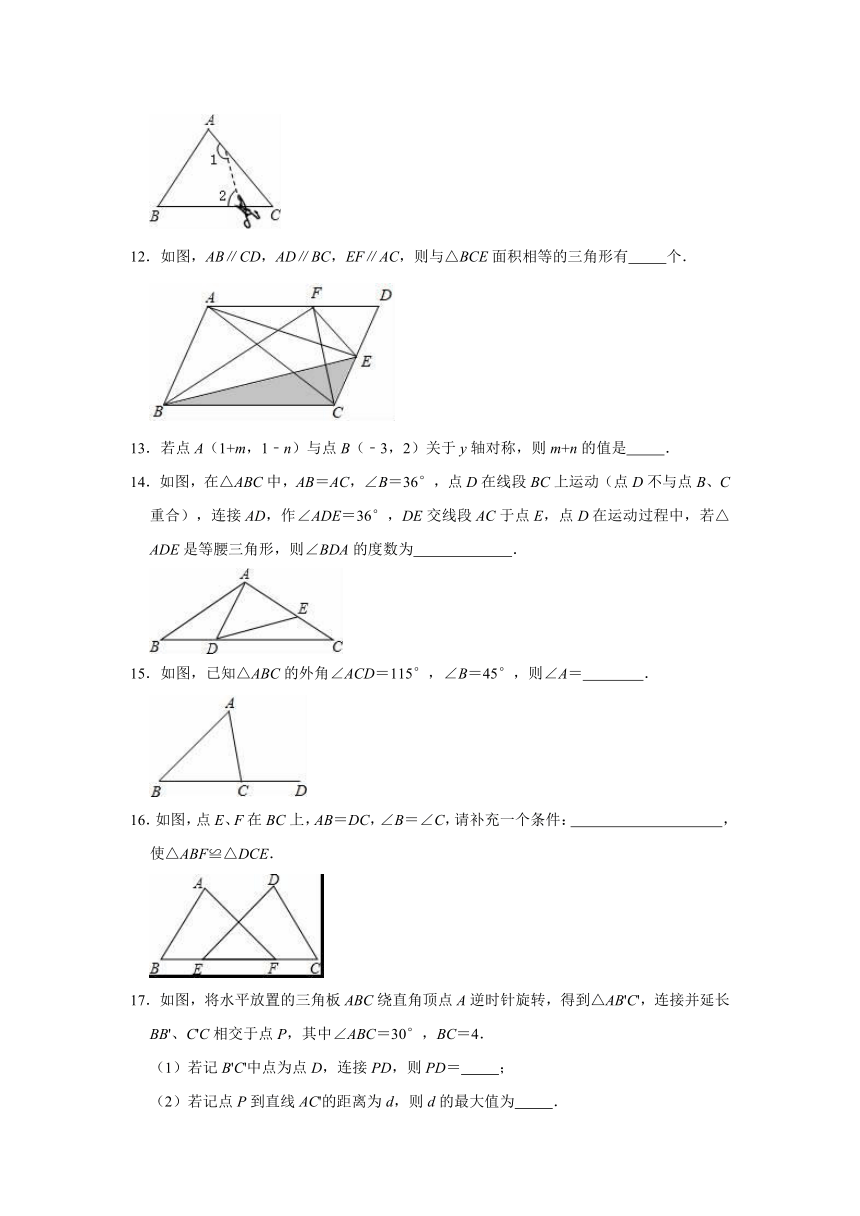
11.如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于
.
12.如图,AB∥CD,AD∥BC,EF∥AC,则与△BCE面积相等的三角形有
个.
13.若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是
.
14.如图,在△ABC中,AB=AC,∠B=36°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=36°,DE交线段AC于点E,点D在运动过程中,若△ADE是等腰三角形,则∠BDA的度数为
.
15.如图,已知△ABC的外角∠ACD=115°,∠B=45°,则∠A=
.
16.如图,点E、F在BC上,AB=DC,∠B=∠C,请补充一个条件:
,使△ABF≌△DCE.
17.如图,将水平放置的三角板ABC绕直角顶点A逆时针旋转,得到△AB'C',连接并延长BB'、C'C相交于点P,其中∠ABC=30°,BC=4.
(1)若记B'C'中点为点D,连接PD,则PD=
;
(2)若记点P到直线AC'的距离为d,则d的最大值为
.
18.我们规定:等腰三角形的顶角与一个底角度数的比值叫作等腰三角形的“特征值”,记作k.若k=2,则该等腰三角形的顶角为
度.
三.解答题(共4小题,满分32分)
19.(6分)化简
(1)
(2).
20.(6分)
21.(10分)如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
22.(10分)如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠B=39°,求∠CAD的度数;
(2)若点E在边AC上,EF∥AB交AD的延长线于点F.求证:AE=FE.
四.解答题(共4小题,满分26分)
23.(8分)建立直角坐标系,解决以下问题:
(1)画出下列各点,并把各点依次连接成封闭图形.
A(﹣2,3),B(2,3),C(5,0),D(2,﹣3),E(﹣2,﹣3),F(﹣5,0).
(2)指出上面各点所在的象限或坐标轴.
(3)分别写出上面各点关于x轴,y轴和原点的对称点.
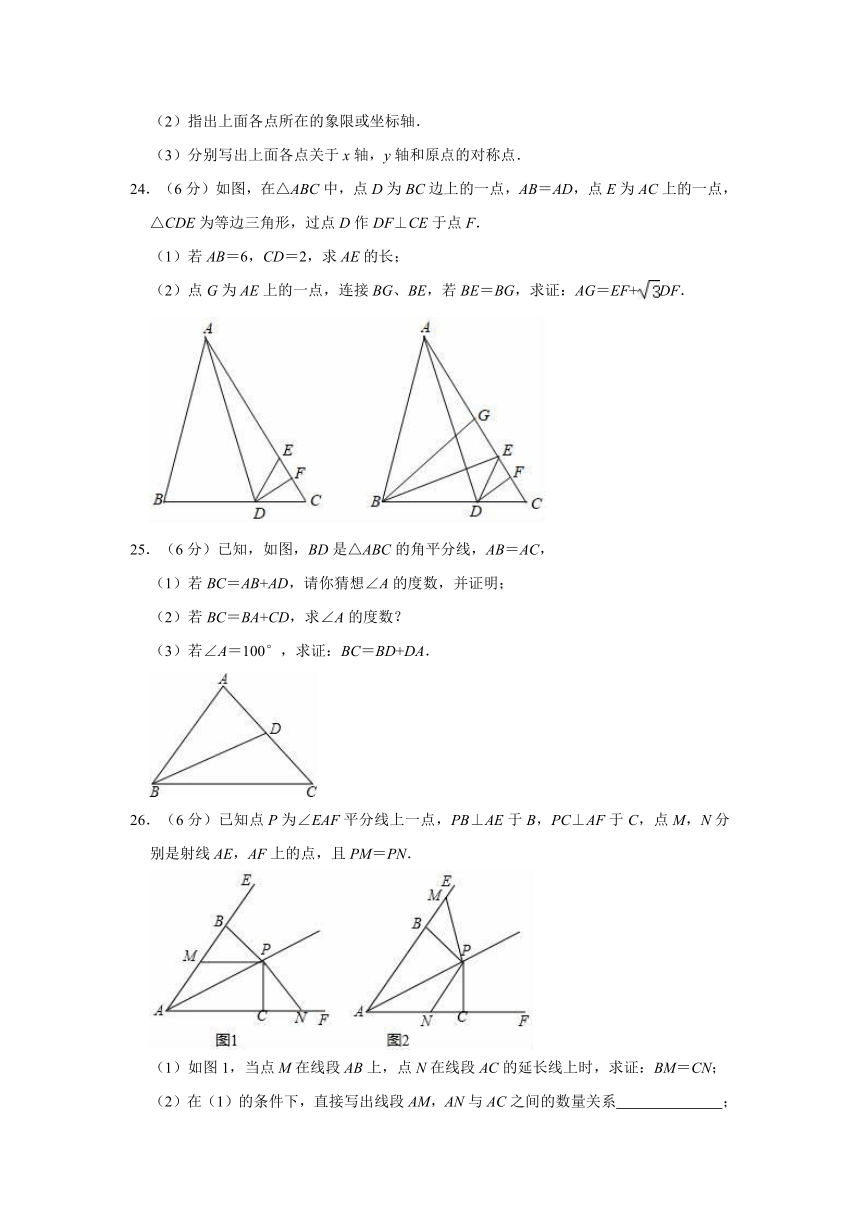
24.(6分)如图,在△ABC中,点D为BC边上的一点,AB=AD,点E为AC上的一点,△CDE为等边三角形,过点D作DF⊥CE于点F.
(1)若AB=6,CD=2,求AE的长;
(2)点G为AE上的一点,连接BG、BE,若BE=BG,求证:AG=EF+DF.
25.(6分)已知,如图,BD是△ABC的角平分线,AB=AC,
(1)若BC=AB+AD,请你猜想∠A的度数,并证明;
(2)若BC=BA+CD,求∠A的度数?
(3)若∠A=100°,求证:BC=BD+DA.
26.(6分)已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M,N分别是射线AE,AF上的点,且PM=PN.
(1)如图1,当点M在线段AB上,点N在线段AC的延长线上时,求证:BM=CN;
(2)在(1)的条件下,直接写出线段AM,AN与AC之间的数量关系
;
(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,若AC:PC=2:1,且PC=4,求四边形ANPM的面积.
参考答案与试题解析
一.选择题(共6小题,满分18分,每小题3分)
1.解:A、是有理数,故此选项不符合题意;
B、0是有理数,故此选项不符合题意;
C、是无理数,故此选项符合题意;
D、=2是有理数,故此选项不符合题意;
故选:C.
2.解:A、×=,故此选项错误;
B、÷=2,故此选项正确;
C、()2=3,故此选项错误;
D、(3)2=18,故此选项错误;
故选:B.
3.解:∵∠C=90°,∠2=∠CDE=30°,
∠3=∠C+∠CDE
=90°+30°
=120°.
∵a∥b,
∴∠4=∠3=120°.
∵∠A=30°
∴∠1=∠4+∠A
=120°+30°
=150°.
故选:C.
4.解:第三边的取值范围是大于4且小于8,又第三边是偶数,故第三边是6.
则该三角形的周长是14.
故选:B.
5.解:∵xy>0,
∴x>0,y>0或x<0,y<0,
∴点P(x,y)在一或三象限.
故选:D.
6.解:A、设∠A=x,则∠B=2x,∠C=3x,
∴x+2x+3x=180°,
解得:x=30°,
∴最大角∠C=3×30°=90°,
∴三角形是直角三角形,选项A不符合题意;
B、∵∠A﹣∠C=∠B,
∴∠A=∠B+∠C,
又∵∠A+∠B+∠C=180°,
∴∠A=180°÷2=90°,
∴三角形是直角三角形,选项B不符合题意;
C、设∠C=y,则∠A=2y,∠B=2y,
∴y+2y+2y=180°,
解得:y=36°,
∴最大角∠B=2×36°=72°,
∴三角形不是直角三角形,选项C符合题意;
D、设∠A=z,则∠B=z,∠C=2z,
∴z+z+2z=180°,
解得:z=45°,
∴最大角∠C=2×45°=90°,
∴三角形是直角三角形,选项D不符合题意.
故选:C.
二.填空题(共12小题,满分24分,每小题2分)
7.解:如果某数的一个平方根是﹣5,那么这个数是25,
故答案为:25
8.解:=3,(﹣1.5)2=2.25,
∵3>2.25,
∴﹣<﹣1.5.
故答案为:<.
9.解:306
070
000=3.0607×108≈3.061×108.
故答案为:3.061×108.
10.解:=
故答案为:.
11.解:∵△ABC中,∠C=50°,
∴∠A+∠B=180°﹣∠C=130°,
∵∠A+∠B+∠1+∠2=360°,
∴∠1+∠2=360°﹣130°=230°,
故答案为:230°.
12.解:∵AB∥CD,
∴△ACE与△BCE的面积相等,
∵EF∥AC,
∴△ACE与△ACF的面积相等,
∵AD∥BC,
∴△ABF与△ACF的面积相等,
∴△BCE面积相等的三角形有△ACE、△ACF,△ABF共3个,
故答案为3.
13.解:∵点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,
∴1+m=3、1﹣n=2,
解得:m=2、n=﹣1,
所以m+n=2﹣1=1,
故答案为:1.
14.解:∵AB=AC,
∴∠B=∠C=36°,
①当AD=AE时,∠ADE=∠AED=36°,
∵∠AED>∠C,
∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=×(180°﹣36°)=72°,
∵∠BAC=180°﹣36°﹣36°=108°,
∴∠BAD=108°﹣72°=36°;
∴∠BDA=180°﹣36°﹣36°=108°;
③当EA=ED时,∠ADE=∠DAE=36°,
∴∠BAD=108°﹣36°=72°,
∴∠BDA=180°﹣72°﹣36°=72°;
∴当△ADE是等腰三角形时,∠BDA的度数是108°或72°.
故答案为:108°或72°.
15.解:∠A=∠ACD﹣∠B=115°﹣45°=70°.
故答案为:70.
16.解:根据SAS判断△ABF≌△DCE,可以添加BE=CF或BF=EC.
根据AAS判断△ABF≌△DCE,可以添加∠AFB=∠DEC.
根据ASA判断△ABF≌△DCE,可以添加∠A=∠D.
故答案为BE=CF或BF=EC或∠A=∠D或∠AFB=∠DEC.
17.解:(1)由旋转的性质得:AC=AC,AB'=AB,∠C'AC=∠B'AB,
∴∠ACC'=∠AC'C,∠ABB'=∠AB'B,
∴∠ACC'=∠AC'C=∠ABB'=∠AB'B,
∵∠B'AB+∠ABB'+∠AB'B=180°,∠B'AB+∠BAC+∠ABB'+∠AC'C+∠BPC'=360°,
∴∠BPC'=90°,
∵D为B'C'中点,
∴PD=BC'=2;
故答案为:2;
(2)连接AD,作DE⊥AC'于E,如图所示:
∵AB'C'=∠ABC=30°,
∴∠AC'B=60°,
∵点D为B'C'中点,
∴AD=BC'=DC',
∴△ADC'是等边三角形,
∴AC'=AD=2,
∵DE⊥AC',
∴AE=AC'=1,DE=AE=,
当P、D、E三点共线时,点P到直线AC'的距离d最大=PD+DE=2+;
故答案为:2+.
18.解:∵k=2,
∴设顶角=2α,则底角=α,
∴α+α+2α=180°,
∴α=45°,
∴该等腰三角形的顶角为90°,
故答案为:90.
三.解答题(共4小题,满分32分)
19.解:(1)原式=2﹣+3=;
(2)原式=﹣3=3﹣6.
20.解:原式=
=23.
21.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
22.解:(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°,
又∠B=39°,
∴∠BAD=∠CAD=90°﹣39°=51°;
(2)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,
∵EF∥AC,
∴∠F=∠CAD,
∴∠BAD=∠F,
∴AE=FE.
四.解答题(共4小题,满分26分)
23.解:(1)如图所示;
(2)A(﹣2,3)在第二象限,
B(2,3)在第一象限,
C(5,0)在x轴的正半轴上,
D(2,﹣3)在第四象限,
E(﹣2,﹣3)在第三象限,
F(﹣5,0)在x轴的负半轴上;
(3)A(﹣2,3),B(2,3),C(5,0),D(2,﹣3),E(﹣2,﹣3),F(﹣5,0)关于x轴的对称点分别为:(﹣2,﹣3),(2,﹣3),(5,0),(2,3),(﹣2,3),(﹣5,0);
A(﹣2,3),B(2,3),C(5,0),D(2,﹣3),E(﹣2,﹣3),F(﹣5,0)关于y轴的对称点分别为:(2,3),(﹣2,3),(﹣5,0),(﹣2,﹣3),(2,﹣3),(5,0);
A(﹣2,3),B(2,3),C(5,0),D(2,﹣3),E(﹣2,﹣3),F(﹣5,0)关于原点的对称点分别为:(2,﹣3),(﹣2,﹣3),(﹣5,0),(﹣2,3),(2,3),(5,0);
24.解:(1)∵△CDE为等边三角形,DF⊥CE,
∴CF=EF=1,∠EDF=30°,
∴DF=EF=,
∴AF===,
∴AE=﹣1;
(2)如图,在AG上截取GN=EC,连接BN,
∵BE=BG,
∴∠BGE=∠BEG,
∴∠BGN=∠BEC,
∵△DEC是等边三角形,
∴DE=EC=DC,∠C=∠DEC=∠EDC=60°,
在△BGN和△BEC中,
,
∴△BGN≌△BEC(SAS),
∴BC=BN,∠C=∠BNG=60°,
∴∠NBC=∠C=60°,
∵∠ABD=∠ADB,
∴∠ABN+∠NBC=∠C+∠DAC,
∴∠ABN=∠DAC,
∵∠BNC=∠DEC=60°,
∴∠ANB=∠AED=120°,
在△ABN和△DAE中,
,
∴△ABN≌△DAE(AAS),
∴AN=DE,
∴AG=AN+NG=DE+EC=2EC,
∵△DEC是等边三角形,DF⊥CE,
∴EF=EC,DF=EF=EC,
∴EF+DF=EC+EC=2EC,
∴AG=EF+DF.
25.解:(1)答:∠A=90°.理由如下:
在BC上截取BE=BA,连接DE.
∵BC=AB+AD,
∴CE=AD,
∵BD是△ABC的角平分线,
∴∠ABD=∠EBD,
∵AB=BE,BD=BD,
∴△ABD≌△EBD,
∴AD=DE=CE,∠A=∠DEB,
∴∠C=∠EDC,
∴∠A=∠DEB=∠C+∠EDC=2∠C,
∵AB=AC,
∴∠C=∠B,
∵∠A+∠ABC+∠C=180°,
∴4∠C=180°,
∴∠C=45°,∠A=2∠C=90°,
即∠A=90°;
(2)解:在BC上截取CF=CD,连接DF.
∵BC=BA+CD,
∴BF=BA,
∵∠ABD=∠FBD,BD=BD,
∴△ABD≌△FBD,
∴∠A=∠DFB,
∵CD=CF,
∴∠CDF=∠CFD,
∴∠C+2∠DFC=180°,
∵∠A+∠DFC=180°,
∴2∠A﹣∠C=180°,
∵∠A+2∠C=180°,
解得:∠A=108°,
答:∠A的度数是108°.
(3)证明:
在BC上截取BQ=BD,连接DQ,延长BA到W使BW=BQ,连接DW.
∵∠A=100°,AC=AB,
∴∠C=∠ABC=40°,
∵BD平分∠ABC,
∴∠DBQ=20°,
∵BD=BQ,
∴∠DQB=∠BDQ=(180°﹣∠DBQ)=80°,
∴∠CDQ=∠DQB﹣∠C=40°=∠C,
∴DQ=CQ,
∵在△WBD和△QBD中
,
∴△WBD≌△QBD,
∴∠W=∠DQB=80°,DW=DQ=CQ,
∵∠BAC=100°,
∴∠WAD=180°﹣∠BAC=180°﹣100°=80°,
即∠WAD=∠W,
∴AD=DW=DQ=CQ,
∴BC=BD+DA.
26.解:(1)如图1,∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF,
∴PB=PC,∠PBM=∠PCN=90°,
∵在Rt△PBM和Rt△PCN中,∠PBM=∠PCN=90°,
,
∴Rt△PBM≌Rt△PCN(HL),
∴BM=CN;
(2)AM+AN=2AC.
∵∠APB=90°﹣∠PAB,∠APC=90°﹣∠PAC,点P为∠EAF平分线上一点,
∴∠APC=∠APB,即AP平分∠CPB,
∵PB⊥AB,PC⊥AC,
∴AB=AC,
又∵BM=CN,
∴AM+AN=(AB﹣MB)+(CN+AC)=AB+AC=2AC;
故答案为:AM+AN=2AC.
(3)如图2,∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF,
∴PB=PC,∠PBM=∠PCN=90°,
∵在Rt△PBM和Rt△PCN中,PBM=∠PCN=90°,
,
∴Rt△PBM≌Rt△PCN(HL),
∴BM=CN,
∴S△PBM=S△PCN
∵AC:PC=2:1,PC=4,
∴AC=8,
∴由(2)可得,AB=AC=8,PB=PC=4,
∴S四边形ANPM=S△APN+S△APB+S△PBM
=S△APN+S△APB+S△PCN
=S△APC+S△APB
=AC?PC+AB?PB
=×8×4+×8×4
=32.
一.选择题(共6小题,满分18分,每小题3分)
1.下列各数中,无理数是( )
A.
B.0
C.
D.
2.下列各式计算正确的是( )
A.×=6
B.÷=2
C.()2=9
D.(3)2=6
3.如图,已知a∥b,一块含30°角的直角三角板,如图所示放置,∠2=30°,则∠1等于( )
A.110°
B.130°
C.150°
D.160°
4.一个三角形的两边长为2和6,第三边为偶数.则这个三角形的周长为( )
A.16
B.14
C.12
D.10
5.若xy>0,则关于点P(x,y)的说法正确的是( )
A.在一或二象限
B.在一或四象限
C.在二或四象限
D.在一或三象限
6.给定下列条件,不能判定三角形是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3
B.∠A﹣∠C=∠B
C.∠A=∠B=2∠C
D.∠A=∠B=∠C
二.填空题(共12小题,满分24分,每小题2分)
7.如果某数的一个平方根是﹣5,那么这个数是
.
8.比较大小:﹣
﹣1.5.
9.将306
070
000用科学记数法表示并保留4个有效数字为
.
10.把化成幂的形式是
.
11.如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于
.
12.如图,AB∥CD,AD∥BC,EF∥AC,则与△BCE面积相等的三角形有
个.
13.若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是
.
14.如图,在△ABC中,AB=AC,∠B=36°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=36°,DE交线段AC于点E,点D在运动过程中,若△ADE是等腰三角形,则∠BDA的度数为
.
15.如图,已知△ABC的外角∠ACD=115°,∠B=45°,则∠A=
.
16.如图,点E、F在BC上,AB=DC,∠B=∠C,请补充一个条件:
,使△ABF≌△DCE.
17.如图,将水平放置的三角板ABC绕直角顶点A逆时针旋转,得到△AB'C',连接并延长BB'、C'C相交于点P,其中∠ABC=30°,BC=4.
(1)若记B'C'中点为点D,连接PD,则PD=
;
(2)若记点P到直线AC'的距离为d,则d的最大值为
.
18.我们规定:等腰三角形的顶角与一个底角度数的比值叫作等腰三角形的“特征值”,记作k.若k=2,则该等腰三角形的顶角为
度.
三.解答题(共4小题,满分32分)
19.(6分)化简
(1)
(2).
20.(6分)
21.(10分)如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
22.(10分)如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠B=39°,求∠CAD的度数;
(2)若点E在边AC上,EF∥AB交AD的延长线于点F.求证:AE=FE.
四.解答题(共4小题,满分26分)
23.(8分)建立直角坐标系,解决以下问题:
(1)画出下列各点,并把各点依次连接成封闭图形.
A(﹣2,3),B(2,3),C(5,0),D(2,﹣3),E(﹣2,﹣3),F(﹣5,0).
(2)指出上面各点所在的象限或坐标轴.
(3)分别写出上面各点关于x轴,y轴和原点的对称点.
24.(6分)如图,在△ABC中,点D为BC边上的一点,AB=AD,点E为AC上的一点,△CDE为等边三角形,过点D作DF⊥CE于点F.
(1)若AB=6,CD=2,求AE的长;
(2)点G为AE上的一点,连接BG、BE,若BE=BG,求证:AG=EF+DF.
25.(6分)已知,如图,BD是△ABC的角平分线,AB=AC,
(1)若BC=AB+AD,请你猜想∠A的度数,并证明;
(2)若BC=BA+CD,求∠A的度数?
(3)若∠A=100°,求证:BC=BD+DA.
26.(6分)已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M,N分别是射线AE,AF上的点,且PM=PN.
(1)如图1,当点M在线段AB上,点N在线段AC的延长线上时,求证:BM=CN;
(2)在(1)的条件下,直接写出线段AM,AN与AC之间的数量关系
;
(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,若AC:PC=2:1,且PC=4,求四边形ANPM的面积.
参考答案与试题解析
一.选择题(共6小题,满分18分,每小题3分)
1.解:A、是有理数,故此选项不符合题意;
B、0是有理数,故此选项不符合题意;
C、是无理数,故此选项符合题意;
D、=2是有理数,故此选项不符合题意;
故选:C.
2.解:A、×=,故此选项错误;
B、÷=2,故此选项正确;
C、()2=3,故此选项错误;
D、(3)2=18,故此选项错误;
故选:B.
3.解:∵∠C=90°,∠2=∠CDE=30°,
∠3=∠C+∠CDE
=90°+30°
=120°.
∵a∥b,
∴∠4=∠3=120°.
∵∠A=30°
∴∠1=∠4+∠A
=120°+30°
=150°.
故选:C.
4.解:第三边的取值范围是大于4且小于8,又第三边是偶数,故第三边是6.
则该三角形的周长是14.
故选:B.
5.解:∵xy>0,
∴x>0,y>0或x<0,y<0,
∴点P(x,y)在一或三象限.
故选:D.
6.解:A、设∠A=x,则∠B=2x,∠C=3x,
∴x+2x+3x=180°,
解得:x=30°,
∴最大角∠C=3×30°=90°,
∴三角形是直角三角形,选项A不符合题意;
B、∵∠A﹣∠C=∠B,
∴∠A=∠B+∠C,
又∵∠A+∠B+∠C=180°,
∴∠A=180°÷2=90°,
∴三角形是直角三角形,选项B不符合题意;
C、设∠C=y,则∠A=2y,∠B=2y,
∴y+2y+2y=180°,
解得:y=36°,
∴最大角∠B=2×36°=72°,
∴三角形不是直角三角形,选项C符合题意;
D、设∠A=z,则∠B=z,∠C=2z,
∴z+z+2z=180°,
解得:z=45°,
∴最大角∠C=2×45°=90°,
∴三角形是直角三角形,选项D不符合题意.
故选:C.
二.填空题(共12小题,满分24分,每小题2分)
7.解:如果某数的一个平方根是﹣5,那么这个数是25,
故答案为:25
8.解:=3,(﹣1.5)2=2.25,
∵3>2.25,
∴﹣<﹣1.5.
故答案为:<.
9.解:306
070
000=3.0607×108≈3.061×108.
故答案为:3.061×108.
10.解:=
故答案为:.
11.解:∵△ABC中,∠C=50°,
∴∠A+∠B=180°﹣∠C=130°,
∵∠A+∠B+∠1+∠2=360°,
∴∠1+∠2=360°﹣130°=230°,
故答案为:230°.
12.解:∵AB∥CD,
∴△ACE与△BCE的面积相等,
∵EF∥AC,
∴△ACE与△ACF的面积相等,
∵AD∥BC,
∴△ABF与△ACF的面积相等,
∴△BCE面积相等的三角形有△ACE、△ACF,△ABF共3个,
故答案为3.
13.解:∵点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,
∴1+m=3、1﹣n=2,
解得:m=2、n=﹣1,
所以m+n=2﹣1=1,
故答案为:1.
14.解:∵AB=AC,
∴∠B=∠C=36°,
①当AD=AE时,∠ADE=∠AED=36°,
∵∠AED>∠C,
∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=×(180°﹣36°)=72°,
∵∠BAC=180°﹣36°﹣36°=108°,
∴∠BAD=108°﹣72°=36°;
∴∠BDA=180°﹣36°﹣36°=108°;
③当EA=ED时,∠ADE=∠DAE=36°,
∴∠BAD=108°﹣36°=72°,
∴∠BDA=180°﹣72°﹣36°=72°;
∴当△ADE是等腰三角形时,∠BDA的度数是108°或72°.
故答案为:108°或72°.
15.解:∠A=∠ACD﹣∠B=115°﹣45°=70°.
故答案为:70.
16.解:根据SAS判断△ABF≌△DCE,可以添加BE=CF或BF=EC.
根据AAS判断△ABF≌△DCE,可以添加∠AFB=∠DEC.
根据ASA判断△ABF≌△DCE,可以添加∠A=∠D.
故答案为BE=CF或BF=EC或∠A=∠D或∠AFB=∠DEC.
17.解:(1)由旋转的性质得:AC=AC,AB'=AB,∠C'AC=∠B'AB,
∴∠ACC'=∠AC'C,∠ABB'=∠AB'B,
∴∠ACC'=∠AC'C=∠ABB'=∠AB'B,
∵∠B'AB+∠ABB'+∠AB'B=180°,∠B'AB+∠BAC+∠ABB'+∠AC'C+∠BPC'=360°,
∴∠BPC'=90°,
∵D为B'C'中点,
∴PD=BC'=2;
故答案为:2;
(2)连接AD,作DE⊥AC'于E,如图所示:
∵AB'C'=∠ABC=30°,
∴∠AC'B=60°,
∵点D为B'C'中点,
∴AD=BC'=DC',
∴△ADC'是等边三角形,
∴AC'=AD=2,
∵DE⊥AC',
∴AE=AC'=1,DE=AE=,
当P、D、E三点共线时,点P到直线AC'的距离d最大=PD+DE=2+;
故答案为:2+.
18.解:∵k=2,
∴设顶角=2α,则底角=α,
∴α+α+2α=180°,
∴α=45°,
∴该等腰三角形的顶角为90°,
故答案为:90.
三.解答题(共4小题,满分32分)
19.解:(1)原式=2﹣+3=;
(2)原式=﹣3=3﹣6.
20.解:原式=
=23.
21.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
22.解:(1)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°,
又∠B=39°,
∴∠BAD=∠CAD=90°﹣39°=51°;
(2)∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,
∵EF∥AC,
∴∠F=∠CAD,
∴∠BAD=∠F,
∴AE=FE.
四.解答题(共4小题,满分26分)
23.解:(1)如图所示;
(2)A(﹣2,3)在第二象限,
B(2,3)在第一象限,
C(5,0)在x轴的正半轴上,
D(2,﹣3)在第四象限,
E(﹣2,﹣3)在第三象限,
F(﹣5,0)在x轴的负半轴上;
(3)A(﹣2,3),B(2,3),C(5,0),D(2,﹣3),E(﹣2,﹣3),F(﹣5,0)关于x轴的对称点分别为:(﹣2,﹣3),(2,﹣3),(5,0),(2,3),(﹣2,3),(﹣5,0);
A(﹣2,3),B(2,3),C(5,0),D(2,﹣3),E(﹣2,﹣3),F(﹣5,0)关于y轴的对称点分别为:(2,3),(﹣2,3),(﹣5,0),(﹣2,﹣3),(2,﹣3),(5,0);
A(﹣2,3),B(2,3),C(5,0),D(2,﹣3),E(﹣2,﹣3),F(﹣5,0)关于原点的对称点分别为:(2,﹣3),(﹣2,﹣3),(﹣5,0),(﹣2,3),(2,3),(5,0);
24.解:(1)∵△CDE为等边三角形,DF⊥CE,
∴CF=EF=1,∠EDF=30°,
∴DF=EF=,
∴AF===,
∴AE=﹣1;
(2)如图,在AG上截取GN=EC,连接BN,
∵BE=BG,
∴∠BGE=∠BEG,
∴∠BGN=∠BEC,
∵△DEC是等边三角形,
∴DE=EC=DC,∠C=∠DEC=∠EDC=60°,
在△BGN和△BEC中,
,
∴△BGN≌△BEC(SAS),
∴BC=BN,∠C=∠BNG=60°,
∴∠NBC=∠C=60°,
∵∠ABD=∠ADB,
∴∠ABN+∠NBC=∠C+∠DAC,
∴∠ABN=∠DAC,
∵∠BNC=∠DEC=60°,
∴∠ANB=∠AED=120°,
在△ABN和△DAE中,
,
∴△ABN≌△DAE(AAS),
∴AN=DE,
∴AG=AN+NG=DE+EC=2EC,
∵△DEC是等边三角形,DF⊥CE,
∴EF=EC,DF=EF=EC,
∴EF+DF=EC+EC=2EC,
∴AG=EF+DF.
25.解:(1)答:∠A=90°.理由如下:
在BC上截取BE=BA,连接DE.
∵BC=AB+AD,
∴CE=AD,
∵BD是△ABC的角平分线,
∴∠ABD=∠EBD,
∵AB=BE,BD=BD,
∴△ABD≌△EBD,
∴AD=DE=CE,∠A=∠DEB,
∴∠C=∠EDC,
∴∠A=∠DEB=∠C+∠EDC=2∠C,
∵AB=AC,
∴∠C=∠B,
∵∠A+∠ABC+∠C=180°,
∴4∠C=180°,
∴∠C=45°,∠A=2∠C=90°,
即∠A=90°;
(2)解:在BC上截取CF=CD,连接DF.
∵BC=BA+CD,
∴BF=BA,
∵∠ABD=∠FBD,BD=BD,
∴△ABD≌△FBD,
∴∠A=∠DFB,
∵CD=CF,
∴∠CDF=∠CFD,
∴∠C+2∠DFC=180°,
∵∠A+∠DFC=180°,
∴2∠A﹣∠C=180°,
∵∠A+2∠C=180°,
解得:∠A=108°,
答:∠A的度数是108°.
(3)证明:
在BC上截取BQ=BD,连接DQ,延长BA到W使BW=BQ,连接DW.
∵∠A=100°,AC=AB,
∴∠C=∠ABC=40°,
∵BD平分∠ABC,
∴∠DBQ=20°,
∵BD=BQ,
∴∠DQB=∠BDQ=(180°﹣∠DBQ)=80°,
∴∠CDQ=∠DQB﹣∠C=40°=∠C,
∴DQ=CQ,
∵在△WBD和△QBD中
,
∴△WBD≌△QBD,
∴∠W=∠DQB=80°,DW=DQ=CQ,
∵∠BAC=100°,
∴∠WAD=180°﹣∠BAC=180°﹣100°=80°,
即∠WAD=∠W,
∴AD=DW=DQ=CQ,
∴BC=BD+DA.
26.解:(1)如图1,∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF,
∴PB=PC,∠PBM=∠PCN=90°,
∵在Rt△PBM和Rt△PCN中,∠PBM=∠PCN=90°,
,
∴Rt△PBM≌Rt△PCN(HL),
∴BM=CN;
(2)AM+AN=2AC.
∵∠APB=90°﹣∠PAB,∠APC=90°﹣∠PAC,点P为∠EAF平分线上一点,
∴∠APC=∠APB,即AP平分∠CPB,
∵PB⊥AB,PC⊥AC,
∴AB=AC,
又∵BM=CN,
∴AM+AN=(AB﹣MB)+(CN+AC)=AB+AC=2AC;
故答案为:AM+AN=2AC.
(3)如图2,∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF,
∴PB=PC,∠PBM=∠PCN=90°,
∵在Rt△PBM和Rt△PCN中,PBM=∠PCN=90°,
,
∴Rt△PBM≌Rt△PCN(HL),
∴BM=CN,
∴S△PBM=S△PCN
∵AC:PC=2:1,PC=4,
∴AC=8,
∴由(2)可得,AB=AC=8,PB=PC=4,
∴S四边形ANPM=S△APN+S△APB+S△PBM
=S△APN+S△APB+S△PCN
=S△APC+S△APB
=AC?PC+AB?PB
=×8×4+×8×4
=32.
同课章节目录
