2020-2021学年沪教新版七年级下册数学期末练习试题(Word版有答案)
文档属性
| 名称 | 2020-2021学年沪教新版七年级下册数学期末练习试题(Word版有答案) | 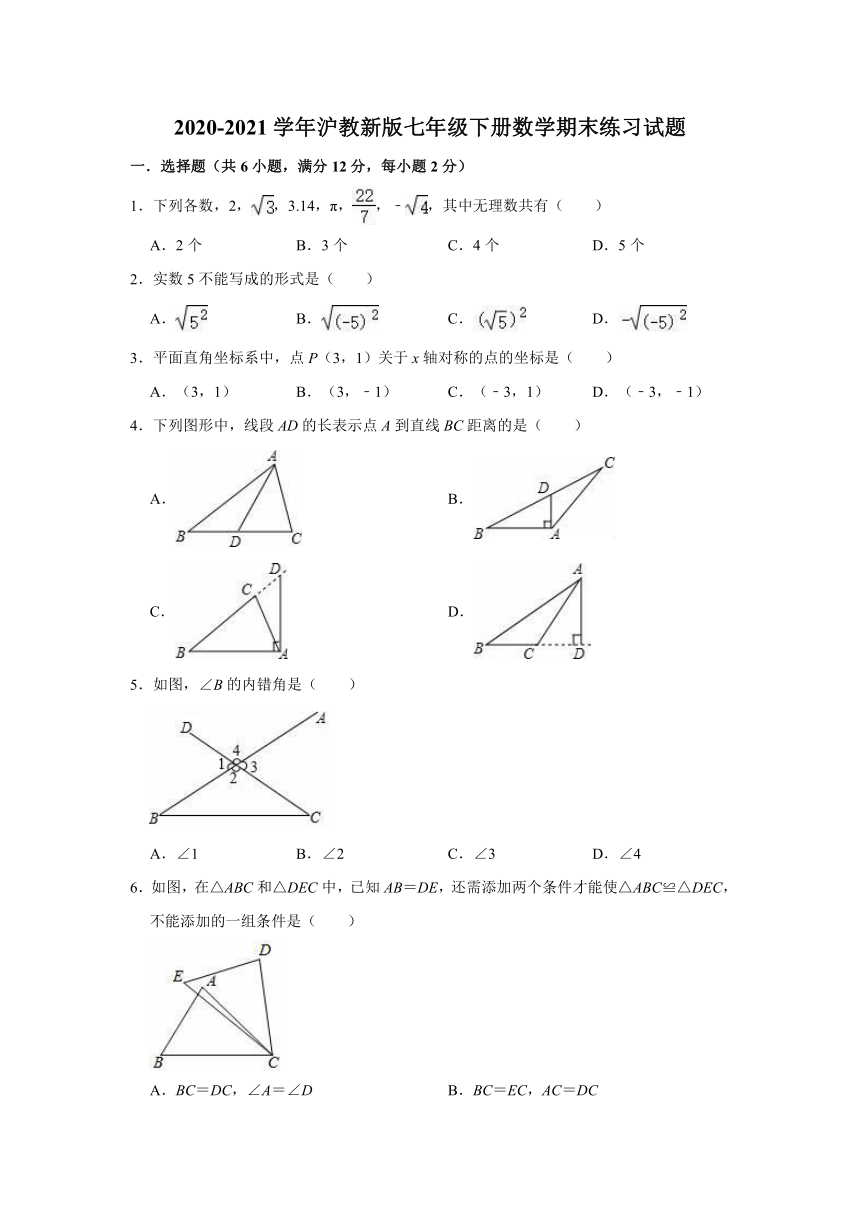 | |
| 格式 | zip | ||
| 文件大小 | 341.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-21 10:29:43 | ||
图片预览



文档简介
2020-2021学年沪教新版七年级下册数学期末练习试题
一.选择题(共6小题,满分12分,每小题2分)
1.下列各数,2,,3.14,π,,﹣,其中无理数共有( )
A.2个
B.3个
C.4个
D.5个
2.实数5不能写成的形式是( )
A.
B.
C.
D.
3.平面直角坐标系中,点P(3,1)关于x轴对称的点的坐标是( )
A.(3,1)
B.(3,﹣1)
C.(﹣3,1)
D.(﹣3,﹣1)
4.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.
B.
C.
D.
5.如图,∠B的内错角是( )
A.∠1
B.∠2
C.∠3
D.∠4
6.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=DC,∠A=∠D
B.BC=EC,AC=DC
C.∠B=∠E,∠BCE=∠ACD
D.BC=EC,∠B=∠E
二.填空题(共12小题,满分24分,每小题2分)
7.如果某数的一个平方根是﹣5,那么这个数是
.
8.比较大小:
.
9.设:=1.732,=5.477,则=
.
10.计算:=
.
11.已知:如图所示,A、B是数轴上的两个点,点A所表示的数为﹣5,动点P以每秒4个单位长度的速度从点B向左运动,同时,动点Q、M从点A向右运动,且点M的速度是点Q速度的,当运动时间为2秒和4秒时,点M和点P的距离都是6个单位长度,则当点P运动到点A时,动点Q所表示的数为
.
12.如图,点A、B分别在x轴和y轴上,OA=1,OB=2,若将线段AB平移至A'B',则a+b的值为
.
13.如果点P在x轴下方,到x轴的距离是5,到y轴的距离是2,那么点P的坐标为
.
14.如图,BD、CE为△ABC的两条角平分线,则图中∠1、∠2、∠A之间的数量关系为
.
15.已知△ABC是等腰三角形,它的周长为20cm,一条边长6cm,那么腰长是
cm.
16.如图:△ABC中,AB=6cm,BC=8cm,AC=7cm,O是∠A、∠B的平分线的交点,过点O作MN∥AB交AC、BC于点M、N则△CMN的周长为
.
17.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE=
.
18.如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,若将△ABC沿DE折叠,使点B与点A重合,则折痕DE的长是
cm.
三.解答题(共9小题,满分64分)
19.(6分)计算:(﹣)÷+.
20.(6分)化简
(1)
(2).
21.(6分)计算:.
22.(6分)在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为
°,△AOB
.(填“是”或“不是”)“灵动三角形”;
(2)若∠BAC=70°,则△AOC
(填“是”或“不是”)“灵动三角形”;
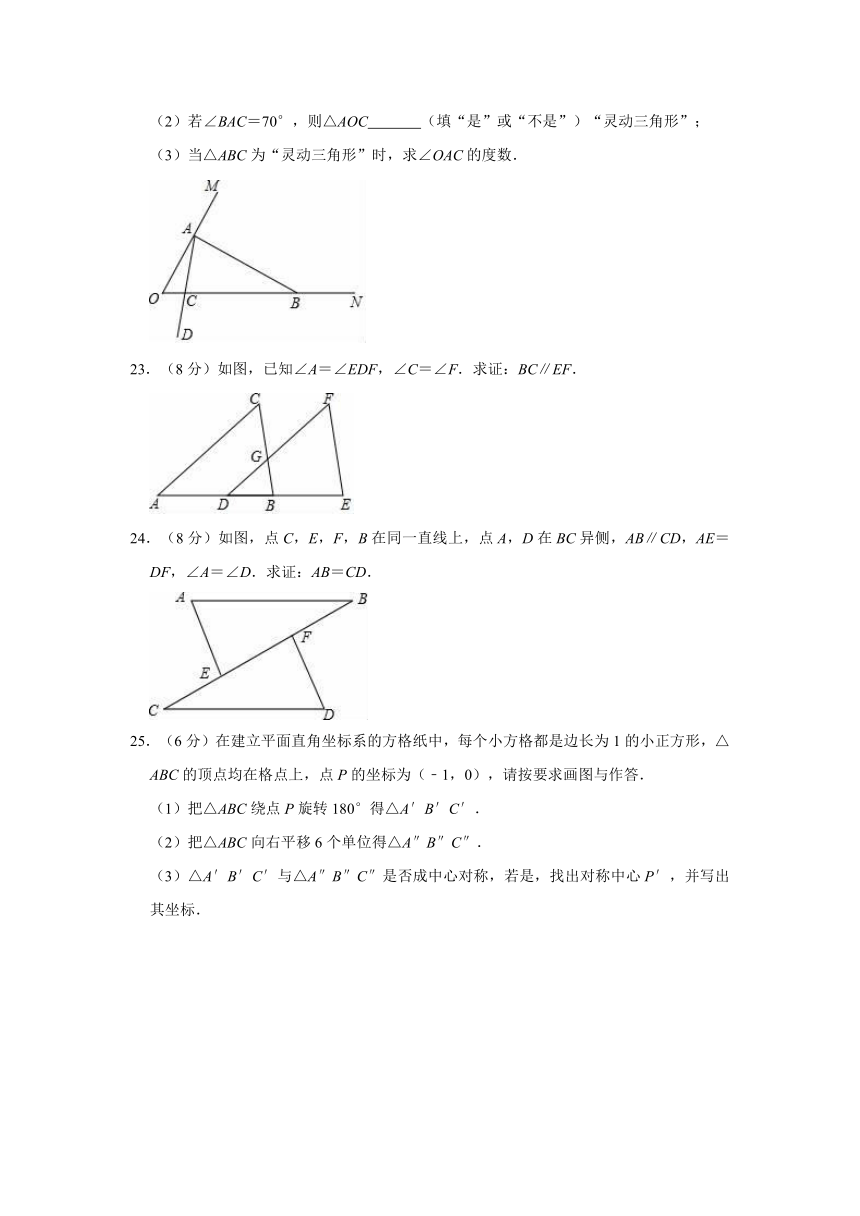
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
23.(8分)如图,已知∠A=∠EDF,∠C=∠F.求证:BC∥EF.
24.(8分)如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.求证:AB=CD.
25.(6分)在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,点P的坐标为(﹣1,0),请按要求画图与作答.
(1)把△ABC绕点P旋转180°得△A′B′C′.
(2)把△ABC向右平移6个单位得△A″B″C″.
(3)△A′B′C′与△A″B″C″是否成中心对称,若是,找出对称中心P′,并写出其坐标.
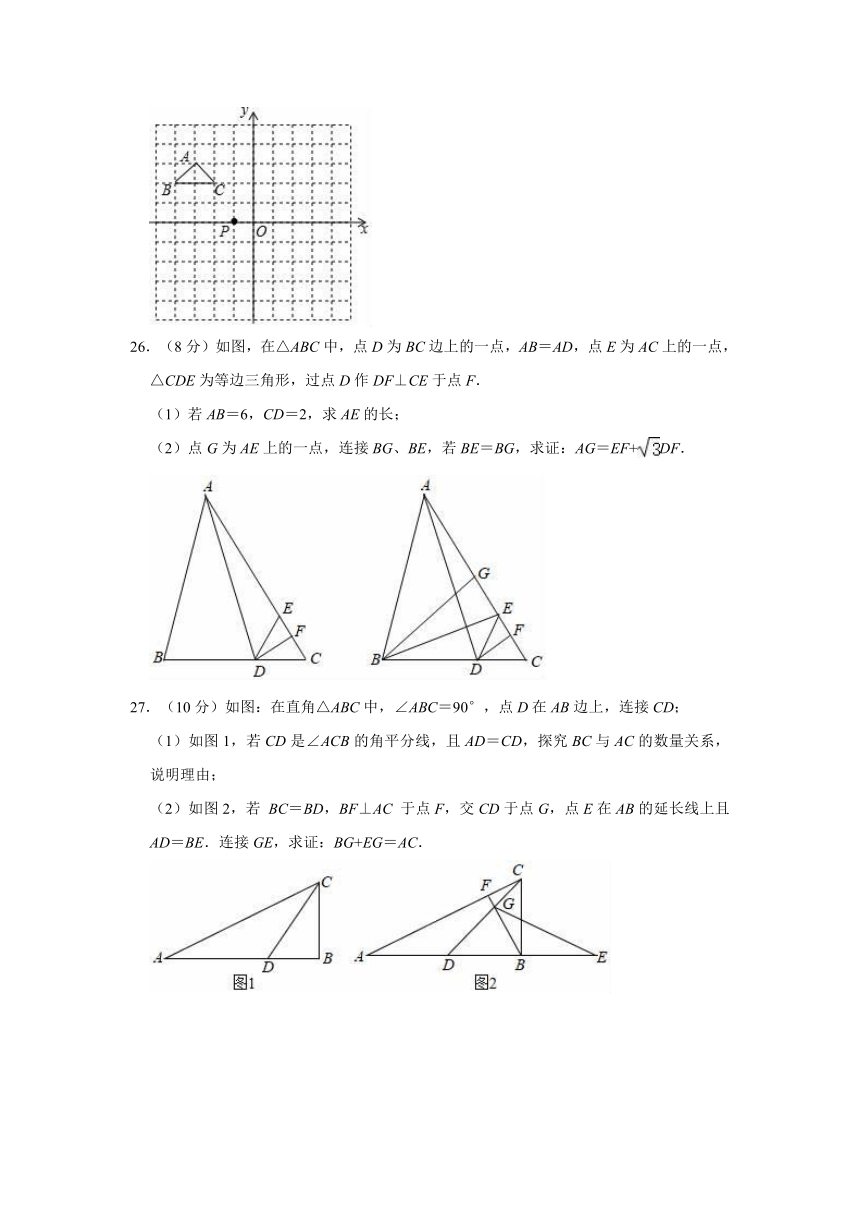
26.(8分)如图,在△ABC中,点D为BC边上的一点,AB=AD,点E为AC上的一点,△CDE为等边三角形,过点D作DF⊥CE于点F.
(1)若AB=6,CD=2,求AE的长;
(2)点G为AE上的一点,连接BG、BE,若BE=BG,求证:AG=EF+DF.
27.(10分)如图:在直角△ABC中,∠ABC=90°,点D在AB边上,连接CD;
(1)如图1,若CD是∠ACB的角平分线,且AD=CD,探究BC与AC的数量关系,说明理由;
(2)如图2,若
BC=BD,BF⊥AC
于点F,交CD于点G,点E在AB的延长线上且AD=BE.连接GE,求证:BG+EG=AC.
参考答案与试题解析
一.选择题(共6小题,满分12分,每小题2分)
1.解:﹣=﹣2,
无理数有,π,共有2个,
故选:A.
2.解:A、=5,
B、=5,
C、()2=5,
D、﹣=﹣5,
故选:D.
3.解:点P(3,1)关于x轴对称的点的坐标是(3,﹣1)
故选:B.
4.解:线段AD的长表示点A到直线BC距离的是图D,
故选:D.
5.解:A、∠B的内错角是∠1,故此选项符合题意;
B、∠B与∠2是同旁内角,故此选项不合题意;
C、∠B与∠3是同位角,故此选项不合题意;
D、∠B与∠4是不是内错角,故此选项不合题意;
故选:A.
6.解:A.AB=DE,BC=DC,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△DEC,故本选项符合题意;
B.AC=DC,AB=DE,BC=EC,符合全等三角形的判定定理SSS,能推出△ABC≌△DEC,故本选项不符合题意;
C.∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
即∠ACB=∠DCE,
∵∠B=∠E,AB=DE,
∴△ABC≌△DEC(AAS),故本选项不符合题意;
D.AB=DE,∠B=∠E,BC=EC,符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故本选项不符合题意;
故选:A.
二.填空题(共12小题,满分24分,每小题2分)
7.解:如果某数的一个平方根是﹣5,那么这个数是25,
故答案为:25
8.解:∵≈1.7,
∴﹣1<1,
∴<.
故答案为:<.
9.解:∵=1.732,而3×102=300
∴=10×1.732=17.32,
故答案为:17.32.
10.解:64===4×4=16.
故答案为:16.
11.解:设点Q运动的速度为每秒a个单位长度,则点M运动的速度为每秒a个单位长度,
由运动时间为2秒和4秒时,点M和点P的距离都是6个单位长度,可列方程,
2×a+6+4×2=4×a+4×4﹣6,
解得,a=6,
a=2,
即:点Q运动的速度为每秒6个单位长度,点M运动的速度为每秒2个单位长度,
此时,AB=2×2+6+4×2=18,
∴点Q所表示的数为﹣5+×6=22,
故答案为:22.
12.解:由作图可知,线段AB向右平移3个单位,再向下平移1个单位得到线段A′B′,
∵A(﹣1,0),B(0,2),
∴A′(2,﹣1),B′(3,1),
∴a=﹣1,b=3,
∴a+b=2,
故答案为:2.
13.解:因为点P在x轴下方,到x轴的距离是5,
所以点P的纵坐标是﹣5;
因为点P到y轴的距离是2,
所以点P的横坐标是2或﹣2,
所以点P的坐标为(2,﹣5)或(﹣2,﹣5).
故答案为:(2,﹣5)或(﹣2,﹣5).
14.解:∵BD、CE为△ABC的两条角平分线,
∴∠ABD=∠ABC,∠ACE=∠ACB,
∵∠1=∠ACE+∠A,∠2=∠ABD+∠A
∴∠1+∠2=∠ACE+∠A+∠ABD+∠A
=∠ACB+∠ACB+∠A+
=90°+
故答案为:∠1+∠2﹣∠A=90°.
15.解:∵等腰三角形的周长为20cm,
∴当腰长=6cm时,底边=20﹣6﹣6=8cm,即6+6>8,能构成三角形,
∴当底边=6cm时,腰长==7cm,即7+6>7,能构成三角形,
∴腰长是6cm或7cm,
故答案为:6或7.
16.解:∵O是∠A、∠B的平分线的交点,
∴∠BAO=∠MAO,∠ABO=∠NBO,
∵MN∥AB,
∴∠MOA=∠BAO,∠BON=∠ABO,
∴∠MOA=∠MAO,∠BON=∠NBO,
∴MA=MO,NO=NB,
∵MN=MO+NO,BC=8cm,AC=7cm,
∴MN=MA+NB,
∴CM+MN+NC=CM+MA+NB+NC=CA+CB=7+8=15cm,
即△CMN的周长为15cm,
故答案为:15cm.
17.解:∵AB=BD,AC=CE,
∴∠BAD=∠BDA,∠E=∠CAE,
设∠BAD=∠BDA=x,∠E=∠CAE=y,
∴∠ABC=∠BAD+∠BDA=2x,∠ACB=∠E+∠CAE=2y,
∵∠ABC+∠ACB+∠BAC=180°,
∴2x+2y+50°=180°,
∴x+y=65°,
∴∠DAE=∠DAB+∠CAE+∠BAC=65°+50°=115°.
故答案为:115°.
18.解:由折叠的性质可得:AD=BD,AE=BE=5,
设DE=x,则可AD=BD=,CD=8﹣,
在RT△ACD中,AC2+CD2=AD2,即36+(8﹣)2=25+x2,
解得:x=,即DE=.
故答案为:.
三.解答题(共9小题,满分64分)
19.解:原式=﹣+
=2﹣+
=.
20.解:(1)原式=2﹣+3=;
(2)原式=﹣3=3﹣6.
21.解:原式=+1﹣÷
=+1﹣4÷8
=+1﹣
=2.
22.解:(1)∵AB⊥OM,
∴∠BAO=90°,
∵∠AOB=60°,
∴∠ABO=90°﹣60°=30°,
∵90°=3×30°,
∴△AOB是“灵动三角形”.
故答案为:30,是.
(2)∵∠OAB=90°,∠BAC=70°,
∴∠OAC=20°,
∵∠AOC=60°=3×20°,
∴△AOC是“灵动三角形”.
故答案为:是.
(3:①∠ACB=3∠ABC时,∠CAB=60°,∠OAC=30°;
②当∠ABC=3∠CAB时,∠CAB=10°,∠OAC=80°.
③当∠ACB=3∠CAB时,∠CAB=37.5°,可得∠OAC=52.5°.
综上所述,满足条件的值为30°或52.5°或80°.
23.证明:∵∠A=∠EDF(已知),
∴AC∥DF(同位角相等,两直线平行),
∴∠C=∠CGF(两直线平行,内错角相等).
又∵∠C=∠F(已知),
∴∠CGF=∠F(等量代换),
∴BC∥EF(内错角相等,两直线平行).
24.解:∵AB∥CD,
∴∠B=∠C,
在△ABE和△DCF中,
,
∴△ABE≌△DCF,
∴AB=CD.
25.解:(1)如图,△A′B′C′为所作;
(2)如图,得△A″B″C″为所作;
(3)如图,P′点为所作;△A′B′C′与△A″B″C″成中心对称,对称中心P′为坐标(2,0).
26.解:(1)∵△CDE为等边三角形,DF⊥CE,
∴CF=EF=1,∠EDF=30°,
∴DF=EF=,
∴AF===,
∴AE=﹣1;
(2)如图,在AG上截取GN=EC,连接BN,
∵BE=BG,
∴∠BGE=∠BEG,
∴∠BGN=∠BEC,
∵△DEC是等边三角形,
∴DE=EC=DC,∠C=∠DEC=∠EDC=60°,
在△BGN和△BEC中,
,
∴△BGN≌△BEC(SAS),
∴BC=BN,∠C=∠BNG=60°,
∴∠NBC=∠C=60°,
∵∠ABD=∠ADB,
∴∠ABN+∠NBC=∠C+∠DAC,
∴∠ABN=∠DAC,
∵∠BNC=∠DEC=60°,
∴∠ANB=∠AED=120°,
在△ABN和△DAE中,
,
∴△ABN≌△DAE(AAS),
∴AN=DE,
∴AG=AN+NG=DE+EC=2EC,
∵△DEC是等边三角形,DF⊥CE,
∴EF=EC,DF=EF=EC,
∴EF+DF=EC+EC=2EC,
∴AG=EF+DF.
27.解:(1)BC=.
理由如下:
如图1,过点D作DM⊥AC于点M,
∵AD=CD,
∴M为AC的中点,
∴CM=AM=AC,
∵CD平分∠ACB,
∴DM=DB,
在Rt△CDM和Rt△CDB中,
,
∴Rt△CDM≌Rt△CDB(HL),
∴CM=CB,
∴BC=AC;
(2)证明:如图2,作DK⊥AB交BF的延长线于点K,
∵BF⊥AC,
∴∠AFK=90°,
∴∠A=∠K,
又∵∠BDK=∠ABC=90°,BC=BD,
∴Rt△CAB≌Rt△BKD(AAS),
∴BK=AC,DK=AB,
∵AD=BE,
∴AD+BD=BE+BD,
即AB=DE,
∴DK=DE,
又∵DB=BC,∠ABC=90°,
∴∠CDB=45°,
∴∠KDG=∠EDG=45°,
又∵DG=DG,
∴△DKG≌△DEG(SAS),
∴KG=EG,
∴AC=BK=KG+BG=EG+BG.
一.选择题(共6小题,满分12分,每小题2分)
1.下列各数,2,,3.14,π,,﹣,其中无理数共有( )
A.2个
B.3个
C.4个
D.5个
2.实数5不能写成的形式是( )
A.
B.
C.
D.
3.平面直角坐标系中,点P(3,1)关于x轴对称的点的坐标是( )
A.(3,1)
B.(3,﹣1)
C.(﹣3,1)
D.(﹣3,﹣1)
4.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.
B.
C.
D.
5.如图,∠B的内错角是( )
A.∠1
B.∠2
C.∠3
D.∠4
6.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=DC,∠A=∠D
B.BC=EC,AC=DC
C.∠B=∠E,∠BCE=∠ACD
D.BC=EC,∠B=∠E
二.填空题(共12小题,满分24分,每小题2分)
7.如果某数的一个平方根是﹣5,那么这个数是
.
8.比较大小:
.
9.设:=1.732,=5.477,则=
.
10.计算:=
.
11.已知:如图所示,A、B是数轴上的两个点,点A所表示的数为﹣5,动点P以每秒4个单位长度的速度从点B向左运动,同时,动点Q、M从点A向右运动,且点M的速度是点Q速度的,当运动时间为2秒和4秒时,点M和点P的距离都是6个单位长度,则当点P运动到点A时,动点Q所表示的数为
.
12.如图,点A、B分别在x轴和y轴上,OA=1,OB=2,若将线段AB平移至A'B',则a+b的值为
.
13.如果点P在x轴下方,到x轴的距离是5,到y轴的距离是2,那么点P的坐标为
.
14.如图,BD、CE为△ABC的两条角平分线,则图中∠1、∠2、∠A之间的数量关系为
.
15.已知△ABC是等腰三角形,它的周长为20cm,一条边长6cm,那么腰长是
cm.
16.如图:△ABC中,AB=6cm,BC=8cm,AC=7cm,O是∠A、∠B的平分线的交点,过点O作MN∥AB交AC、BC于点M、N则△CMN的周长为
.
17.如图,在△ABC中,D,E分别在边CB和BC的延长线上,BD=BA,CE=CA,若∠BAC=50°,则∠DAE=
.
18.如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,若将△ABC沿DE折叠,使点B与点A重合,则折痕DE的长是
cm.
三.解答题(共9小题,满分64分)
19.(6分)计算:(﹣)÷+.
20.(6分)化简
(1)
(2).
21.(6分)计算:.
22.(6分)在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为
°,△AOB
.(填“是”或“不是”)“灵动三角形”;
(2)若∠BAC=70°,则△AOC
(填“是”或“不是”)“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
23.(8分)如图,已知∠A=∠EDF,∠C=∠F.求证:BC∥EF.
24.(8分)如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.求证:AB=CD.
25.(6分)在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,点P的坐标为(﹣1,0),请按要求画图与作答.
(1)把△ABC绕点P旋转180°得△A′B′C′.
(2)把△ABC向右平移6个单位得△A″B″C″.
(3)△A′B′C′与△A″B″C″是否成中心对称,若是,找出对称中心P′,并写出其坐标.
26.(8分)如图,在△ABC中,点D为BC边上的一点,AB=AD,点E为AC上的一点,△CDE为等边三角形,过点D作DF⊥CE于点F.
(1)若AB=6,CD=2,求AE的长;
(2)点G为AE上的一点,连接BG、BE,若BE=BG,求证:AG=EF+DF.
27.(10分)如图:在直角△ABC中,∠ABC=90°,点D在AB边上,连接CD;
(1)如图1,若CD是∠ACB的角平分线,且AD=CD,探究BC与AC的数量关系,说明理由;
(2)如图2,若
BC=BD,BF⊥AC
于点F,交CD于点G,点E在AB的延长线上且AD=BE.连接GE,求证:BG+EG=AC.
参考答案与试题解析
一.选择题(共6小题,满分12分,每小题2分)
1.解:﹣=﹣2,
无理数有,π,共有2个,
故选:A.
2.解:A、=5,
B、=5,
C、()2=5,
D、﹣=﹣5,
故选:D.
3.解:点P(3,1)关于x轴对称的点的坐标是(3,﹣1)
故选:B.
4.解:线段AD的长表示点A到直线BC距离的是图D,
故选:D.
5.解:A、∠B的内错角是∠1,故此选项符合题意;
B、∠B与∠2是同旁内角,故此选项不合题意;
C、∠B与∠3是同位角,故此选项不合题意;
D、∠B与∠4是不是内错角,故此选项不合题意;
故选:A.
6.解:A.AB=DE,BC=DC,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△DEC,故本选项符合题意;
B.AC=DC,AB=DE,BC=EC,符合全等三角形的判定定理SSS,能推出△ABC≌△DEC,故本选项不符合题意;
C.∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
即∠ACB=∠DCE,
∵∠B=∠E,AB=DE,
∴△ABC≌△DEC(AAS),故本选项不符合题意;
D.AB=DE,∠B=∠E,BC=EC,符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故本选项不符合题意;
故选:A.
二.填空题(共12小题,满分24分,每小题2分)
7.解:如果某数的一个平方根是﹣5,那么这个数是25,
故答案为:25
8.解:∵≈1.7,
∴﹣1<1,
∴<.
故答案为:<.
9.解:∵=1.732,而3×102=300
∴=10×1.732=17.32,
故答案为:17.32.
10.解:64===4×4=16.
故答案为:16.
11.解:设点Q运动的速度为每秒a个单位长度,则点M运动的速度为每秒a个单位长度,
由运动时间为2秒和4秒时,点M和点P的距离都是6个单位长度,可列方程,
2×a+6+4×2=4×a+4×4﹣6,
解得,a=6,
a=2,
即:点Q运动的速度为每秒6个单位长度,点M运动的速度为每秒2个单位长度,
此时,AB=2×2+6+4×2=18,
∴点Q所表示的数为﹣5+×6=22,
故答案为:22.
12.解:由作图可知,线段AB向右平移3个单位,再向下平移1个单位得到线段A′B′,
∵A(﹣1,0),B(0,2),
∴A′(2,﹣1),B′(3,1),
∴a=﹣1,b=3,
∴a+b=2,
故答案为:2.
13.解:因为点P在x轴下方,到x轴的距离是5,
所以点P的纵坐标是﹣5;
因为点P到y轴的距离是2,
所以点P的横坐标是2或﹣2,
所以点P的坐标为(2,﹣5)或(﹣2,﹣5).
故答案为:(2,﹣5)或(﹣2,﹣5).
14.解:∵BD、CE为△ABC的两条角平分线,
∴∠ABD=∠ABC,∠ACE=∠ACB,
∵∠1=∠ACE+∠A,∠2=∠ABD+∠A
∴∠1+∠2=∠ACE+∠A+∠ABD+∠A
=∠ACB+∠ACB+∠A+
=90°+
故答案为:∠1+∠2﹣∠A=90°.
15.解:∵等腰三角形的周长为20cm,
∴当腰长=6cm时,底边=20﹣6﹣6=8cm,即6+6>8,能构成三角形,
∴当底边=6cm时,腰长==7cm,即7+6>7,能构成三角形,
∴腰长是6cm或7cm,
故答案为:6或7.
16.解:∵O是∠A、∠B的平分线的交点,
∴∠BAO=∠MAO,∠ABO=∠NBO,
∵MN∥AB,
∴∠MOA=∠BAO,∠BON=∠ABO,
∴∠MOA=∠MAO,∠BON=∠NBO,
∴MA=MO,NO=NB,
∵MN=MO+NO,BC=8cm,AC=7cm,
∴MN=MA+NB,
∴CM+MN+NC=CM+MA+NB+NC=CA+CB=7+8=15cm,
即△CMN的周长为15cm,
故答案为:15cm.
17.解:∵AB=BD,AC=CE,
∴∠BAD=∠BDA,∠E=∠CAE,
设∠BAD=∠BDA=x,∠E=∠CAE=y,
∴∠ABC=∠BAD+∠BDA=2x,∠ACB=∠E+∠CAE=2y,
∵∠ABC+∠ACB+∠BAC=180°,
∴2x+2y+50°=180°,
∴x+y=65°,
∴∠DAE=∠DAB+∠CAE+∠BAC=65°+50°=115°.
故答案为:115°.
18.解:由折叠的性质可得:AD=BD,AE=BE=5,
设DE=x,则可AD=BD=,CD=8﹣,
在RT△ACD中,AC2+CD2=AD2,即36+(8﹣)2=25+x2,
解得:x=,即DE=.
故答案为:.
三.解答题(共9小题,满分64分)
19.解:原式=﹣+
=2﹣+
=.
20.解:(1)原式=2﹣+3=;
(2)原式=﹣3=3﹣6.
21.解:原式=+1﹣÷
=+1﹣4÷8
=+1﹣
=2.
22.解:(1)∵AB⊥OM,
∴∠BAO=90°,
∵∠AOB=60°,
∴∠ABO=90°﹣60°=30°,
∵90°=3×30°,
∴△AOB是“灵动三角形”.
故答案为:30,是.
(2)∵∠OAB=90°,∠BAC=70°,
∴∠OAC=20°,
∵∠AOC=60°=3×20°,
∴△AOC是“灵动三角形”.
故答案为:是.
(3:①∠ACB=3∠ABC时,∠CAB=60°,∠OAC=30°;
②当∠ABC=3∠CAB时,∠CAB=10°,∠OAC=80°.
③当∠ACB=3∠CAB时,∠CAB=37.5°,可得∠OAC=52.5°.
综上所述,满足条件的值为30°或52.5°或80°.
23.证明:∵∠A=∠EDF(已知),
∴AC∥DF(同位角相等,两直线平行),
∴∠C=∠CGF(两直线平行,内错角相等).
又∵∠C=∠F(已知),
∴∠CGF=∠F(等量代换),
∴BC∥EF(内错角相等,两直线平行).
24.解:∵AB∥CD,
∴∠B=∠C,
在△ABE和△DCF中,
,
∴△ABE≌△DCF,
∴AB=CD.
25.解:(1)如图,△A′B′C′为所作;
(2)如图,得△A″B″C″为所作;
(3)如图,P′点为所作;△A′B′C′与△A″B″C″成中心对称,对称中心P′为坐标(2,0).
26.解:(1)∵△CDE为等边三角形,DF⊥CE,
∴CF=EF=1,∠EDF=30°,
∴DF=EF=,
∴AF===,
∴AE=﹣1;
(2)如图,在AG上截取GN=EC,连接BN,
∵BE=BG,
∴∠BGE=∠BEG,
∴∠BGN=∠BEC,
∵△DEC是等边三角形,
∴DE=EC=DC,∠C=∠DEC=∠EDC=60°,
在△BGN和△BEC中,
,
∴△BGN≌△BEC(SAS),
∴BC=BN,∠C=∠BNG=60°,
∴∠NBC=∠C=60°,
∵∠ABD=∠ADB,
∴∠ABN+∠NBC=∠C+∠DAC,
∴∠ABN=∠DAC,
∵∠BNC=∠DEC=60°,
∴∠ANB=∠AED=120°,
在△ABN和△DAE中,
,
∴△ABN≌△DAE(AAS),
∴AN=DE,
∴AG=AN+NG=DE+EC=2EC,
∵△DEC是等边三角形,DF⊥CE,
∴EF=EC,DF=EF=EC,
∴EF+DF=EC+EC=2EC,
∴AG=EF+DF.
27.解:(1)BC=.
理由如下:
如图1,过点D作DM⊥AC于点M,
∵AD=CD,
∴M为AC的中点,
∴CM=AM=AC,
∵CD平分∠ACB,
∴DM=DB,
在Rt△CDM和Rt△CDB中,
,
∴Rt△CDM≌Rt△CDB(HL),
∴CM=CB,
∴BC=AC;
(2)证明:如图2,作DK⊥AB交BF的延长线于点K,
∵BF⊥AC,
∴∠AFK=90°,
∴∠A=∠K,
又∵∠BDK=∠ABC=90°,BC=BD,
∴Rt△CAB≌Rt△BKD(AAS),
∴BK=AC,DK=AB,
∵AD=BE,
∴AD+BD=BE+BD,
即AB=DE,
∴DK=DE,
又∵DB=BC,∠ABC=90°,
∴∠CDB=45°,
∴∠KDG=∠EDG=45°,
又∵DG=DG,
∴△DKG≌△DEG(SAS),
∴KG=EG,
∴AC=BK=KG+BG=EG+BG.
同课章节目录
