_2020-2021学年人教版七年级数学下册 9.1.1 不等式及其解集 教学设计(表格式)
文档属性
| 名称 | _2020-2021学年人教版七年级数学下册 9.1.1 不等式及其解集 教学设计(表格式) |  | |
| 格式 | doc | ||
| 文件大小 | 40.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-22 13:18:05 | ||
图片预览

文档简介
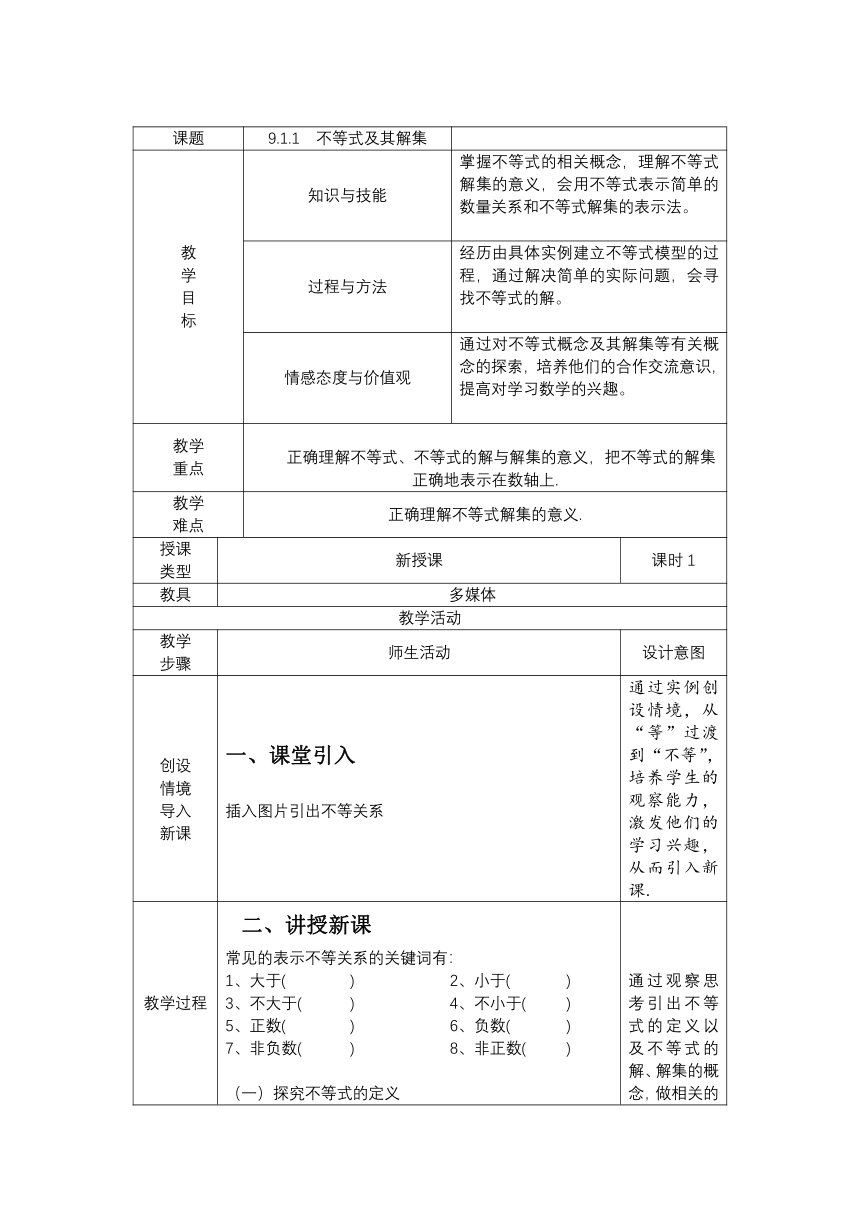
课题 9.1.1 不等式及其解集
教 学
目
标 知识与技能 掌握不等式的相关概念,理解不等式解集的意义,会用不等式表示简单的数量关系和不等式解集的表示法。
过程与方法 经历由具体实例建立不等式模型的过程,通过解决简单的实际问题,会寻找不等式的解。
情感态度与价值观 通过对不等式概念及其解集等有关概念的探索,培养他们的合作交流意识,提高对学习数学的兴趣。
教学 重点
正确理解不等式、不等式的解与解集的意义,把不等式的解集正确地表示在数轴上.
教学 难点 正确理解不等式解集的意义.
授课 类型 新授课 课时1
教具 多媒体
教学活动
教学 步骤 师生活动 设计意图
创设
情境
导入
新课 一、课堂引入
插入图片引出不等关系
通过实例创设情境,从“等”过渡到“不等”,培养学生的观察能力,激发他们的学习兴趣,从而引入新课.
教学过程 二、讲授新课
常见的表示不等关系的关键词有:
1、大于( ) 2、小于( )
3、不大于( ) 4、不小于( )
5、正数( ) 6、负数( )
7、非负数( ) 8、非正数( )
(一)探究不等式的定义
不等式的定义:用不等号连接的式子叫做不等式。
不等式中常见的不等号有五种:
“>”、“<”、 “≥”、“≤” 、“≠”
例1:下列哪些式子是不等式?哪些不是,为什么?
(1)、3<2 (2)、5>-2
(3)、m+3≠0 (4)、x+y
(5)、2x-5=0 (6)、3x+2y≥6
(7)、5x-1≤-x+3
请你按照题目的意思列出不等式
a是正数
b是负数
m与5的和小于7
n与2的差不大于-1
x的4倍大于8
(6)y的一半不小于3
(二)、不等式的解和解集以及解不等式的概念
例2:下列数中,哪些是不等式x+3>6的解?哪些不是?
-4;-2.5;0;1;2.5;3;3.2;4.8;8;12
一个含有未知数的不等式的所有的解的集合叫做不等式的解集。
例3:你能一眼看出下列不等式的解集吗?
(1)x+3>6; (2)2x<8;
(3)x-2 ≥ 0 (4)x-1 ≤ 2
求不等式解集的过程叫做解不等式
(三)、用数轴表示不等式的解集
不等式解集的表示方法.
(1)用式子表示;(2)用数轴表示.
例4:怎样表示不等式x<10 的解集?
练习:用数轴表示不等式的解集
通过观察思考引出不等式的定义以及不等式的解、解集的概念,做相关的练习加深印象,熟练知识点.
课堂小结
【课堂小结】
1.不等式的定义:用<,>,≠, ≥, ≤ 连接的式子叫做不等式。
2.能使不等式成立的未知数的值,叫做不等式的解.
3.一个不等式的所有解,组成这个不等式的解集.
4.求不等式解集的过程叫做解不等式.
5.不等式解集的表示方法.
(1)用式子表示;(2)用数轴表示 考查学生的认知度
课后作业 【课后作业】
必做题:
习题第120页2,3
选做题:
练习册第71页6,7 通过练习进一步巩固不等式的知识.
板书设计
【板书设计】
9.1.1不等式及其解集
1、不等式的概念
2、一元一次不等式的概念
3、不等式的解集
4、不等式的解集在数轴上的表示
5、巩固练习解
6、小结
7、作业
课件
相关问题
分析
简明清楚
重点突出,加深学生对重点知识的理解和掌握
教学反思
教 学
目
标 知识与技能 掌握不等式的相关概念,理解不等式解集的意义,会用不等式表示简单的数量关系和不等式解集的表示法。
过程与方法 经历由具体实例建立不等式模型的过程,通过解决简单的实际问题,会寻找不等式的解。
情感态度与价值观 通过对不等式概念及其解集等有关概念的探索,培养他们的合作交流意识,提高对学习数学的兴趣。
教学 重点
正确理解不等式、不等式的解与解集的意义,把不等式的解集正确地表示在数轴上.
教学 难点 正确理解不等式解集的意义.
授课 类型 新授课 课时1
教具 多媒体
教学活动
教学 步骤 师生活动 设计意图
创设
情境
导入
新课 一、课堂引入
插入图片引出不等关系
通过实例创设情境,从“等”过渡到“不等”,培养学生的观察能力,激发他们的学习兴趣,从而引入新课.
教学过程 二、讲授新课
常见的表示不等关系的关键词有:
1、大于( ) 2、小于( )
3、不大于( ) 4、不小于( )
5、正数( ) 6、负数( )
7、非负数( ) 8、非正数( )
(一)探究不等式的定义
不等式的定义:用不等号连接的式子叫做不等式。
不等式中常见的不等号有五种:
“>”、“<”、 “≥”、“≤” 、“≠”
例1:下列哪些式子是不等式?哪些不是,为什么?
(1)、3<2 (2)、5>-2
(3)、m+3≠0 (4)、x+y
(5)、2x-5=0 (6)、3x+2y≥6
(7)、5x-1≤-x+3
请你按照题目的意思列出不等式
a是正数
b是负数
m与5的和小于7
n与2的差不大于-1
x的4倍大于8
(6)y的一半不小于3
(二)、不等式的解和解集以及解不等式的概念
例2:下列数中,哪些是不等式x+3>6的解?哪些不是?
-4;-2.5;0;1;2.5;3;3.2;4.8;8;12
一个含有未知数的不等式的所有的解的集合叫做不等式的解集。
例3:你能一眼看出下列不等式的解集吗?
(1)x+3>6; (2)2x<8;
(3)x-2 ≥ 0 (4)x-1 ≤ 2
求不等式解集的过程叫做解不等式
(三)、用数轴表示不等式的解集
不等式解集的表示方法.
(1)用式子表示;(2)用数轴表示.
例4:怎样表示不等式x<10 的解集?
练习:用数轴表示不等式的解集
通过观察思考引出不等式的定义以及不等式的解、解集的概念,做相关的练习加深印象,熟练知识点.
课堂小结
【课堂小结】
1.不等式的定义:用<,>,≠, ≥, ≤ 连接的式子叫做不等式。
2.能使不等式成立的未知数的值,叫做不等式的解.
3.一个不等式的所有解,组成这个不等式的解集.
4.求不等式解集的过程叫做解不等式.
5.不等式解集的表示方法.
(1)用式子表示;(2)用数轴表示 考查学生的认知度
课后作业 【课后作业】
必做题:
习题第120页2,3
选做题:
练习册第71页6,7 通过练习进一步巩固不等式的知识.
板书设计
【板书设计】
9.1.1不等式及其解集
1、不等式的概念
2、一元一次不等式的概念
3、不等式的解集
4、不等式的解集在数轴上的表示
5、巩固练习解
6、小结
7、作业
课件
相关问题
分析
简明清楚
重点突出,加深学生对重点知识的理解和掌握
教学反思
