2020-2021学年七年级数学苏科版下册《第9章乘法公式与因式分解》期末复习能力提升训练1(Word版 附答案)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册《第9章乘法公式与因式分解》期末复习能力提升训练1(Word版 附答案) |  | |
| 格式 | doc | ||
| 文件大小 | 64.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-22 13:18:59 | ||
图片预览

文档简介
2021年度苏科版七年级数学下册《第9章乘法公式与因式分解》
期末复习能力提升训练1(附答案)
1.下列运算正确的是( )
A.(a﹣2)﹣3=a6 B.3a2?2a=6a2
C.a4÷a2=2 D.(a+1)2=a2+1
2.下列运算正确的是( )
A.(x2y)3=x6y B.3x2+4x2=7x4
C.(﹣x)9÷(﹣x)3=x6 D.﹣x(x2﹣x+1)=﹣x3﹣x2﹣x
3.如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3 B.3 C.0 D.1
4.下列从左到右的变形,错误的是( )
A.﹣m+n=﹣(m+n) B.﹣a﹣b=﹣(a+b)
C.(m﹣n)3=﹣(n﹣m)3 D.(y﹣x)2=(x﹣y)2
5.如图,矩形ABCD的周长是10cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为17cm2,那么矩形ABCD的面积是( )
A.3cm2 B.4cm2 C.5cm2 D.6cm2
6.已知多项式x2+4x+k2是一个完全平方式,则k的值为( )
A.2 B.4 C.2或﹣2 D.4或﹣4
7.在下列多项式的乘法中,可以用平方差公式计算的是( )
A.(2x+y)(2y﹣x) B.(x+1)(﹣x﹣1)
C.(3x﹣y)(3x+y) D.(x﹣y)(﹣x+y)
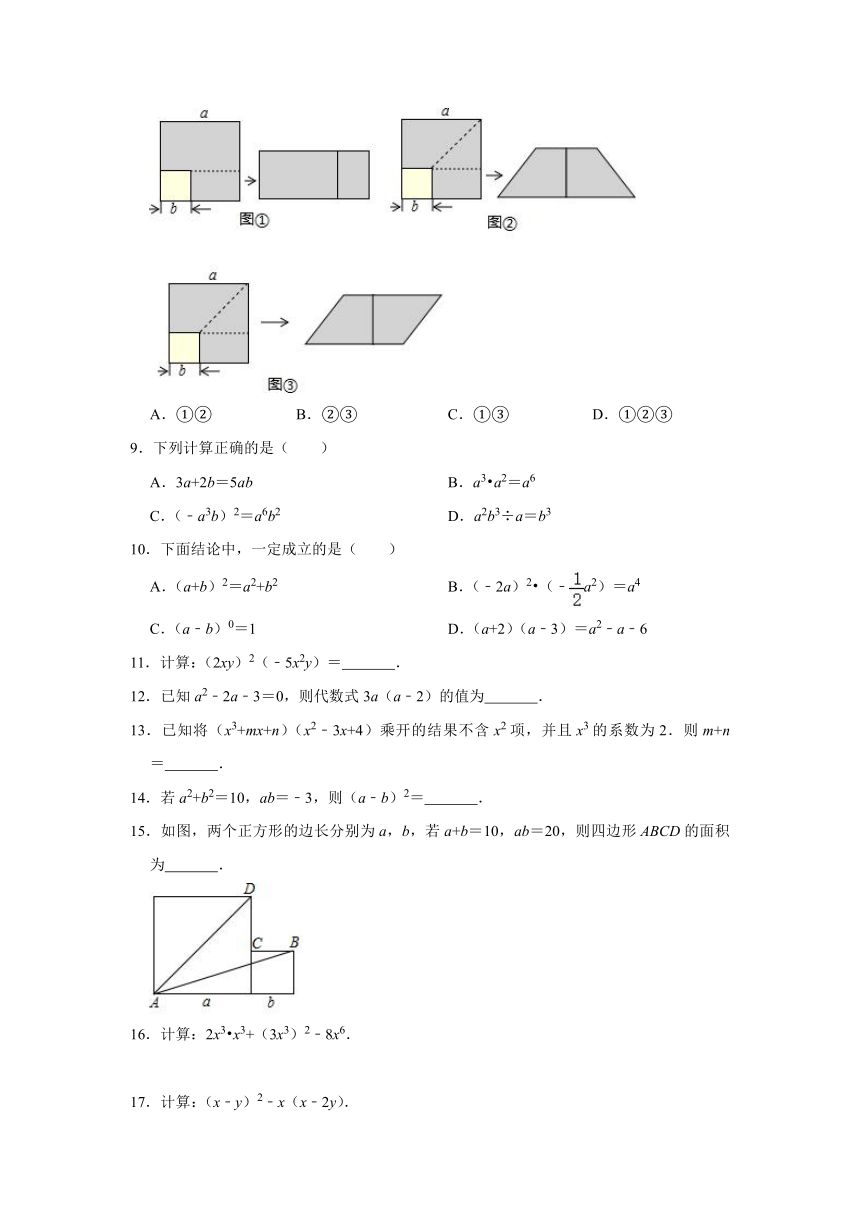
8.如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是( )
A.①② B.②③ C.①③ D.①②③
9.下列计算正确的是( )
A.3a+2b=5ab B.a3?a2=a6
C.(﹣a3b)2=a6b2 D.a2b3÷a=b3
10.下面结论中,一定成立的是( )
A.(a+b)2=a2+b2 B.(﹣2a)2?(﹣a2)=a4
C.(a﹣b)0=1 D.(a+2)(a﹣3)=a2﹣a﹣6
11.计算:(2xy)2(﹣5x2y)= .
12.已知a2﹣2a﹣3=0,则代数式3a(a﹣2)的值为 .
13.已知将(x3+mx+n)(x2﹣3x+4)乘开的结果不含x2项,并且x3的系数为2.则m+n= .
14.若a2+b2=10,ab=﹣3,则(a﹣b)2= .
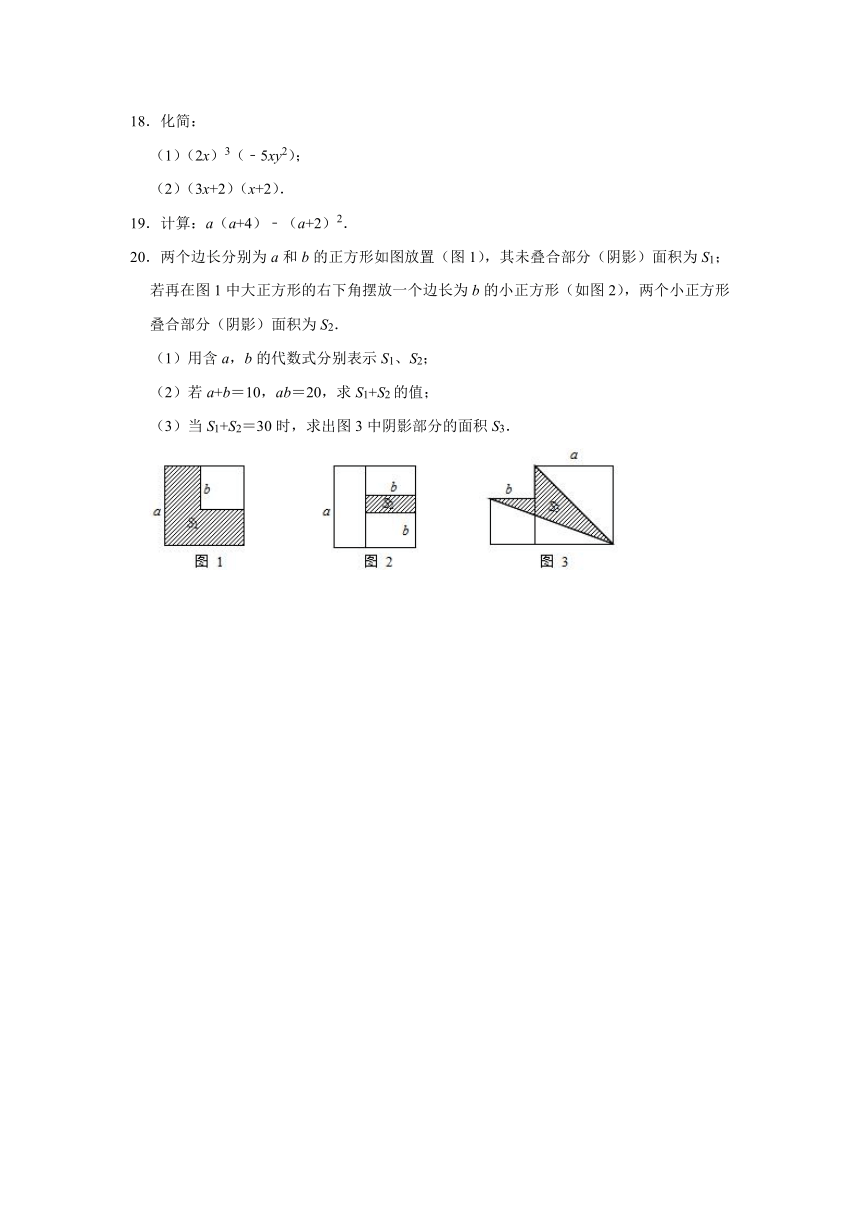
15.如图,两个正方形的边长分别为a,b,若a+b=10,ab=20,则四边形ABCD的面积为 .
16.计算:2x3?x3+(3x3)2﹣8x6.
17.计算:(x﹣y)2﹣x(x﹣2y).
18.化简:
(1)(2x)3(﹣5xy2);
(2)(3x+2)(x+2).
19.计算:a(a+4)﹣(a+2)2.
20.两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a,b的代数式分别表示S1、S2;
(2)若a+b=10,ab=20,求S1+S2的值;
(3)当S1+S2=30时,求出图3中阴影部分的面积S3.
参考答案
1.解:A.(a﹣2)﹣3=a6,故本选项正确;
B.3a2?2a=6a3,故本选项错误;
C.a4÷a2=a2,故本选项错误;
D.(a+1)2=a2+2a+1,故本选项错误;
故选:A.
2.解:A、(x2y)3=x6y3,本选项错误;
B、3x2+4x2=7x2,本选项错误;
C、(﹣x)9÷(﹣x)3=x6,本选项正确;
D、﹣x(x2﹣x+1)=﹣x3+x2﹣x,本选项错误;
故选:C.
3.解:∵(x+m)(x+3)=x2+3x+mx+3m=x2+(3+m)x+3m,
又∵(x+m)与(x+3)的乘积中不含x的一次项,
∴3+m=0,
解得m=﹣3.
故选:A.
4.解:A、﹣m+n=﹣(m﹣n),原变形错误,故本选项符合题意;
B、﹣a﹣b=﹣(a+b),原变形正确,故本选项不符合题意;
C、(m﹣n)3=(m﹣n)(n﹣m)2=﹣(n﹣m)(n﹣m)2=﹣(n﹣m)3,原变形正确,故本选项不符合题意;
D、(y﹣x)2=y2﹣2xy+x2=(x﹣y)2,原变形正确,故本选项不符合题意.
故选:A.
5.解:设AB=x,AD=y,
∵正方形ABEF和ADGH的面积之和为17cm2
∴x2+y2=17,
∵矩形ABCD的周长是10cm
∴2(x+y)=10,
∵(x+y)2=x2+2xy+y2,
∴25=17+2xy,
∴xy=4,
∴矩形ABCD的面积为:xy=4cm2,
故选:B.
6.解:∵多项式x2+4x+k2是一个完全平方式,
∴k=±2,
即k=2或﹣2.
故选:C.
7.解:A、(2x+y)(2y﹣x),不能用平方差公式进行计算,故本选项不符合题意;
B、(x+1)(﹣x﹣1),不能用平方差公式进行计算,故本选项不符合题意;
C、(3x﹣y)(3x+y),能用平方差公式进行计算,故本选项符合题意;
D、(x﹣y)(﹣x+y)不能用平方差公式进行计算,故本选项不符合题意;
故选:C.
8.解:在图①中,左边的图形阴影部分的面积=a2﹣b2,右边图形中阴影部分的面积=(a+b)(a﹣b),故可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式;
在图②中,阴影部分的面积相等,左边阴影部分的面积=a2﹣b2,右边阴影部分面积=(2b+2a)?(a﹣b)=(a+b)(a﹣b),可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式;
在图③中,阴影部分的面积相等,左边阴影部分的面积=a2﹣b2,右边阴影部分面积=(a+b)?(a﹣b),可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式.
故选:D.
9.解:A、3a与2b不是同类项,不能合并,原计算错误,故此选项不符合题意;
B、a3?a2=a5,原计算错误,故此选项不符合题意;
C、(﹣a3b)2=a6b2,原计算正确,故此选项符合题意;
D、a2b3÷a=ab3,原计算错误,故此选项不符合题意.
故选:C.
10.解:A、原式=a2+2ab+b2,
所以A选项错误;
B、原式=﹣a4,
所以B选项错误;
C、当a﹣b≠0时,原式=1,
所以C选项错误;
D选项一定成立.
故选:D.
11.解:原式=4x2y2?(﹣5x2y)=﹣20x4y3.故答案为:﹣20x4y3.
12.解:∵a2﹣2a﹣3=0,
∴a2﹣2a=3,
∴3a(a﹣2)=3(a2﹣2a)=3×3=9.
故答案为:9.
13.解:(x3+mx+n)(x2﹣3x+4)
=x5﹣3x4+4x3+mx3﹣3mx2+4mx+nx2﹣3nx+4n
=x5﹣3x4+(4+m)x3+(﹣3m+n)x2+4mx﹣3nx+4n,
∵结果不含x2项,并且x3的系数为2,
∴﹣3m+n=0,4+m=2,
∴m=﹣2,n=﹣6,
∴m+n=﹣2﹣6=﹣8,
故答案为:﹣8.
14.解:∵(a﹣b)2=a2﹣2ab+b2,a2+b2=10,ab=﹣3,
∴(a﹣b)2=10﹣2×(﹣3)=10+6=16.
故答案为:16.
15.解:根据题意可得,四边形ABCD的面积
=(a2+b2)﹣﹣b(a+b)=(a2+b2﹣ab)
=(a2+b2+2ab﹣3ab)=[(a+b)2﹣3ab];
代入a+b=10,ab=20,可得:
四边形ABCD的面积=(10×10﹣20×3)÷2=20.
故答案为:20.
16.解:2x3?x3+(3x3)2﹣8x6=2x6+9x6﹣8x6=3x6.
17.解:(x﹣y)2﹣x(x﹣2y)=x2﹣2xy+y2﹣x2+2xy=y2.
18.解:(1)原式=8x3?(﹣5xy2)=﹣8x3?5xy2=﹣40x4y2;
(2)原式=3x2+6x+2x+4=3x2+8x+4.
19.解:a(a+4)﹣(a+2)2=a2+4a﹣a2﹣4a﹣4=﹣4.
20.解:(1)由图可得,S1=a2﹣b2,
S2=a2﹣a(a﹣b)﹣b(a﹣b)﹣b(a﹣b)=2b2﹣ab;
(2)S1+S2=a2﹣b2+2b2﹣ab=a2+b2﹣ab,
∵a+b=10,ab=20,
∴S1+S2=a2+b2﹣ab=(a+b)2﹣3ab=100﹣3×20=40;
(3)由图可得,S3=a2+b2﹣b(a+b)﹣a2=(a2+b2﹣ab),
∵S1+S2=a2+b2﹣ab=30,
∴S3=×30=15
期末复习能力提升训练1(附答案)
1.下列运算正确的是( )
A.(a﹣2)﹣3=a6 B.3a2?2a=6a2
C.a4÷a2=2 D.(a+1)2=a2+1
2.下列运算正确的是( )
A.(x2y)3=x6y B.3x2+4x2=7x4
C.(﹣x)9÷(﹣x)3=x6 D.﹣x(x2﹣x+1)=﹣x3﹣x2﹣x
3.如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3 B.3 C.0 D.1
4.下列从左到右的变形,错误的是( )
A.﹣m+n=﹣(m+n) B.﹣a﹣b=﹣(a+b)
C.(m﹣n)3=﹣(n﹣m)3 D.(y﹣x)2=(x﹣y)2
5.如图,矩形ABCD的周长是10cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为17cm2,那么矩形ABCD的面积是( )
A.3cm2 B.4cm2 C.5cm2 D.6cm2
6.已知多项式x2+4x+k2是一个完全平方式,则k的值为( )
A.2 B.4 C.2或﹣2 D.4或﹣4
7.在下列多项式的乘法中,可以用平方差公式计算的是( )
A.(2x+y)(2y﹣x) B.(x+1)(﹣x﹣1)
C.(3x﹣y)(3x+y) D.(x﹣y)(﹣x+y)
8.如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是( )
A.①② B.②③ C.①③ D.①②③
9.下列计算正确的是( )
A.3a+2b=5ab B.a3?a2=a6
C.(﹣a3b)2=a6b2 D.a2b3÷a=b3
10.下面结论中,一定成立的是( )
A.(a+b)2=a2+b2 B.(﹣2a)2?(﹣a2)=a4
C.(a﹣b)0=1 D.(a+2)(a﹣3)=a2﹣a﹣6
11.计算:(2xy)2(﹣5x2y)= .
12.已知a2﹣2a﹣3=0,则代数式3a(a﹣2)的值为 .
13.已知将(x3+mx+n)(x2﹣3x+4)乘开的结果不含x2项,并且x3的系数为2.则m+n= .
14.若a2+b2=10,ab=﹣3,则(a﹣b)2= .
15.如图,两个正方形的边长分别为a,b,若a+b=10,ab=20,则四边形ABCD的面积为 .
16.计算:2x3?x3+(3x3)2﹣8x6.
17.计算:(x﹣y)2﹣x(x﹣2y).
18.化简:
(1)(2x)3(﹣5xy2);
(2)(3x+2)(x+2).
19.计算:a(a+4)﹣(a+2)2.
20.两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a,b的代数式分别表示S1、S2;
(2)若a+b=10,ab=20,求S1+S2的值;
(3)当S1+S2=30时,求出图3中阴影部分的面积S3.
参考答案
1.解:A.(a﹣2)﹣3=a6,故本选项正确;
B.3a2?2a=6a3,故本选项错误;
C.a4÷a2=a2,故本选项错误;
D.(a+1)2=a2+2a+1,故本选项错误;
故选:A.
2.解:A、(x2y)3=x6y3,本选项错误;
B、3x2+4x2=7x2,本选项错误;
C、(﹣x)9÷(﹣x)3=x6,本选项正确;
D、﹣x(x2﹣x+1)=﹣x3+x2﹣x,本选项错误;
故选:C.
3.解:∵(x+m)(x+3)=x2+3x+mx+3m=x2+(3+m)x+3m,
又∵(x+m)与(x+3)的乘积中不含x的一次项,
∴3+m=0,
解得m=﹣3.
故选:A.
4.解:A、﹣m+n=﹣(m﹣n),原变形错误,故本选项符合题意;
B、﹣a﹣b=﹣(a+b),原变形正确,故本选项不符合题意;
C、(m﹣n)3=(m﹣n)(n﹣m)2=﹣(n﹣m)(n﹣m)2=﹣(n﹣m)3,原变形正确,故本选项不符合题意;
D、(y﹣x)2=y2﹣2xy+x2=(x﹣y)2,原变形正确,故本选项不符合题意.
故选:A.
5.解:设AB=x,AD=y,
∵正方形ABEF和ADGH的面积之和为17cm2
∴x2+y2=17,
∵矩形ABCD的周长是10cm
∴2(x+y)=10,
∵(x+y)2=x2+2xy+y2,
∴25=17+2xy,
∴xy=4,
∴矩形ABCD的面积为:xy=4cm2,
故选:B.
6.解:∵多项式x2+4x+k2是一个完全平方式,
∴k=±2,
即k=2或﹣2.
故选:C.
7.解:A、(2x+y)(2y﹣x),不能用平方差公式进行计算,故本选项不符合题意;
B、(x+1)(﹣x﹣1),不能用平方差公式进行计算,故本选项不符合题意;
C、(3x﹣y)(3x+y),能用平方差公式进行计算,故本选项符合题意;
D、(x﹣y)(﹣x+y)不能用平方差公式进行计算,故本选项不符合题意;
故选:C.
8.解:在图①中,左边的图形阴影部分的面积=a2﹣b2,右边图形中阴影部分的面积=(a+b)(a﹣b),故可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式;
在图②中,阴影部分的面积相等,左边阴影部分的面积=a2﹣b2,右边阴影部分面积=(2b+2a)?(a﹣b)=(a+b)(a﹣b),可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式;
在图③中,阴影部分的面积相等,左边阴影部分的面积=a2﹣b2,右边阴影部分面积=(a+b)?(a﹣b),可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式.
故选:D.
9.解:A、3a与2b不是同类项,不能合并,原计算错误,故此选项不符合题意;
B、a3?a2=a5,原计算错误,故此选项不符合题意;
C、(﹣a3b)2=a6b2,原计算正确,故此选项符合题意;
D、a2b3÷a=ab3,原计算错误,故此选项不符合题意.
故选:C.
10.解:A、原式=a2+2ab+b2,
所以A选项错误;
B、原式=﹣a4,
所以B选项错误;
C、当a﹣b≠0时,原式=1,
所以C选项错误;
D选项一定成立.
故选:D.
11.解:原式=4x2y2?(﹣5x2y)=﹣20x4y3.故答案为:﹣20x4y3.
12.解:∵a2﹣2a﹣3=0,
∴a2﹣2a=3,
∴3a(a﹣2)=3(a2﹣2a)=3×3=9.
故答案为:9.
13.解:(x3+mx+n)(x2﹣3x+4)
=x5﹣3x4+4x3+mx3﹣3mx2+4mx+nx2﹣3nx+4n
=x5﹣3x4+(4+m)x3+(﹣3m+n)x2+4mx﹣3nx+4n,
∵结果不含x2项,并且x3的系数为2,
∴﹣3m+n=0,4+m=2,
∴m=﹣2,n=﹣6,
∴m+n=﹣2﹣6=﹣8,
故答案为:﹣8.
14.解:∵(a﹣b)2=a2﹣2ab+b2,a2+b2=10,ab=﹣3,
∴(a﹣b)2=10﹣2×(﹣3)=10+6=16.
故答案为:16.
15.解:根据题意可得,四边形ABCD的面积
=(a2+b2)﹣﹣b(a+b)=(a2+b2﹣ab)
=(a2+b2+2ab﹣3ab)=[(a+b)2﹣3ab];
代入a+b=10,ab=20,可得:
四边形ABCD的面积=(10×10﹣20×3)÷2=20.
故答案为:20.
16.解:2x3?x3+(3x3)2﹣8x6=2x6+9x6﹣8x6=3x6.
17.解:(x﹣y)2﹣x(x﹣2y)=x2﹣2xy+y2﹣x2+2xy=y2.
18.解:(1)原式=8x3?(﹣5xy2)=﹣8x3?5xy2=﹣40x4y2;
(2)原式=3x2+6x+2x+4=3x2+8x+4.
19.解:a(a+4)﹣(a+2)2=a2+4a﹣a2﹣4a﹣4=﹣4.
20.解:(1)由图可得,S1=a2﹣b2,
S2=a2﹣a(a﹣b)﹣b(a﹣b)﹣b(a﹣b)=2b2﹣ab;
(2)S1+S2=a2﹣b2+2b2﹣ab=a2+b2﹣ab,
∵a+b=10,ab=20,
∴S1+S2=a2+b2﹣ab=(a+b)2﹣3ab=100﹣3×20=40;
(3)由图可得,S3=a2+b2﹣b(a+b)﹣a2=(a2+b2﹣ab),
∵S1+S2=a2+b2﹣ab=30,
∴S3=×30=15
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
