第四章 三角形 单元练习卷2020-2021学年北师大版七年级数学下册(Word版 含解析)
文档属性
| 名称 | 第四章 三角形 单元练习卷2020-2021学年北师大版七年级数学下册(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 180.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-21 10:43:09 | ||
图片预览


文档简介
第4章 三角形
一.选择题
1.一个钝角三角形的三条角平分线所在的直线一定交于一点,这交点一定在( )
A.三角形内部 B.三角形的一边上
C.三角形外部 D.三角形的某个顶点上
2.下列各组线段中,能组成三角形的是( )
A.4,5,6 B.6,8,15 C.5,7,12 D.3,9,13
3.锐角三角形中,最大角α的取值范围是( )
A.60°≤α<90° B.60°<α<180° C.60°<α<90° D.0°<α<90°
4.下列判断正确的是( )
A.有两边和其中一边的对角对应相等的两个三角形全等
B.有两边对应相等,且有一角为30°的两个等腰三角形全等
C.有一角和一边对应相等的两个直角三角形全等
D.有两角和一边对应相等的两个三角形全等
5.已知等腰三角形的一个角为75°,则其顶角为( )
A.30° B.75° C.105° D.30°或75°
6.已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( )
A.4对 B.3对 C.2对 D.1对
二.填空题
7.如果在△ABC中,两边a=7cm,b=3cm,则c的取值范围是 .
8.四条线段的长分别为5cm,6cm,8cm,13cm,以其中任意三条线段为边可以构成 个三角形.
9.一个等腰三角形的两边长分别是3cm和7cm,则它的周长是 cm.
10.在Rt△ABC中,锐角∠A的平分线与锐角∠B的平分线相交于点D,则∠ADB= .
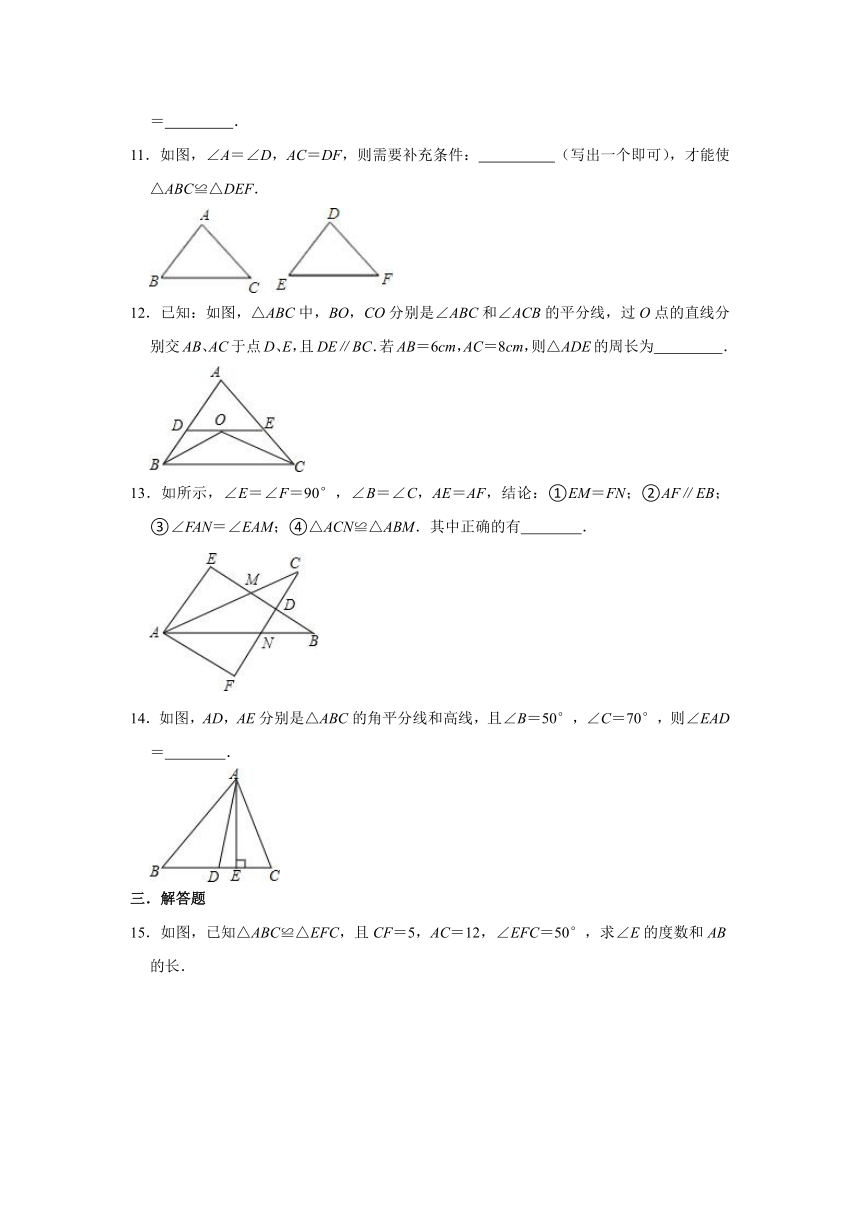
11.如图,∠A=∠D,AC=DF,则需要补充条件: (写出一个即可),才能使△ABC≌△DEF.
12.已知:如图,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6cm,AC=8cm,则△ADE的周长为 .
13.如所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF∥EB;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有 .
14.如图,AD,AE分别是△ABC的角平分线和高线,且∠B=50°,∠C=70°,则∠EAD= .
三.解答题
15.如图,已知△ABC≌△EFC,且CF=5,AC=12,∠EFC=50°,求∠E的度数和AB的长.
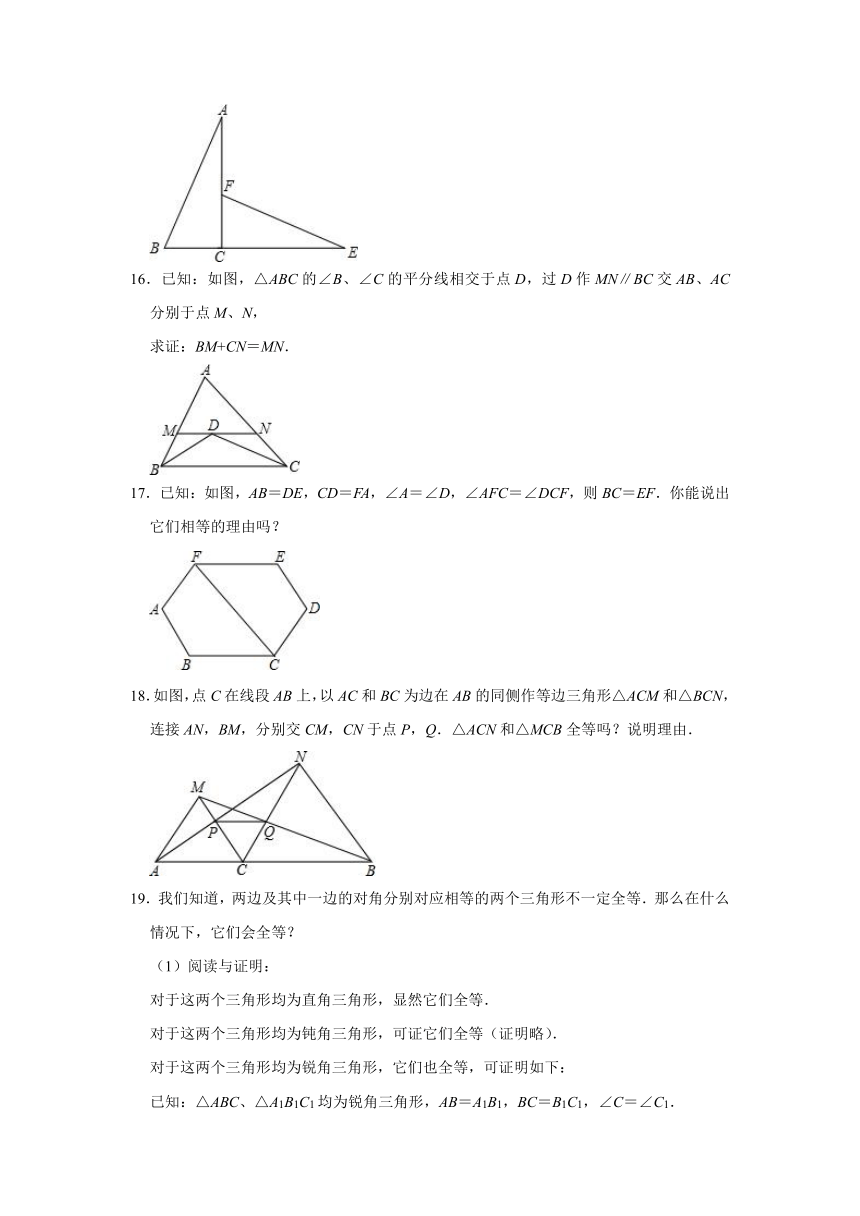
16.已知:如图,△ABC的∠B、∠C的平分线相交于点D,过D作MN∥BC交AB、AC分别于点M、N,
求证:BM+CN=MN.
17.已知:如图,AB=DE,CD=FA,∠A=∠D,∠AFC=∠DCF,则BC=EF.你能说出它们相等的理由吗?
18.如图,点C在线段AB上,以AC和BC为边在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM,分别交CM,CN于点P,Q.△ACN和△MCB全等吗?说明理由.
19.我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等?
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
求证:△ABC≌△A1B1C1.
(请你将下列证明过程补充完整.)
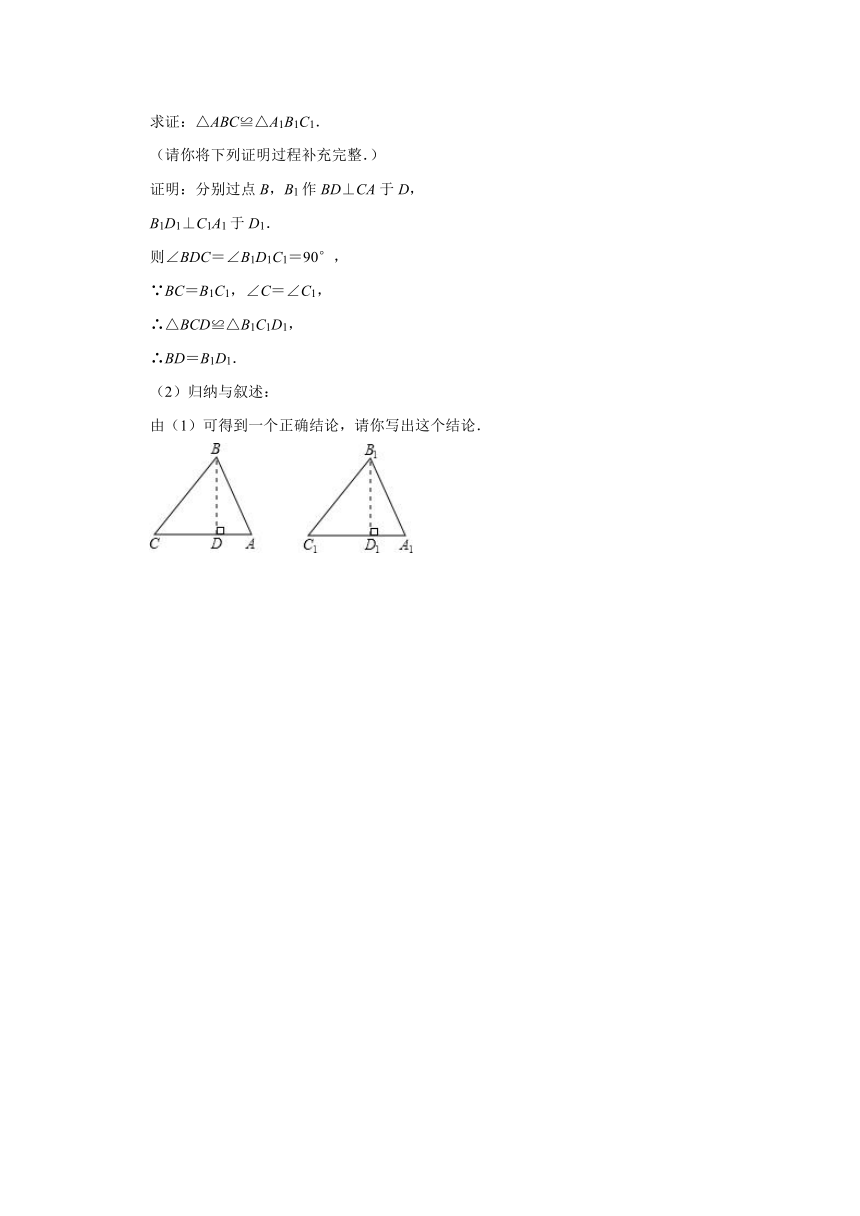
证明:分别过点B,B1作BD⊥CA于D,
B1D1⊥C1A1于D1.
则∠BDC=∠B1D1C1=90°,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,
∴BD=B1D1.
(2)归纳与叙述:
由(1)可得到一个正确结论,请你写出这个结论.
第4章 三角形
参考答案与试题解析
一.选择题
1.一个钝角三角形的三条角平分线所在的直线一定交于一点,这交点一定在( )
A.三角形内部 B.三角形的一边上
C.三角形外部 D.三角形的某个顶点上
【分析】根据三角形的高的性质即可判断.
【解答】解:一个钝角三角形的三条角平分线所在的直线一定交于一点,这交点一定在三角形的内部.
故选:A.
2.下列各组线段中,能组成三角形的是( )
A.4,5,6 B.6,8,15 C.5,7,12 D.3,9,13
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
【解答】解:A、4+5>6,5﹣4<6,能够组成三角形;
B、6+8<15,不能构成三角形;
C、5+7=12,不能构成三角形;
D、3+9<13,不能构成三角形.
故选:A.
3.锐角三角形中,最大角α的取值范围是( )
A.60°≤α<90° B.60°<α<180° C.60°<α<90° D.0°<α<90°
【分析】根据三角形的内角和是180°可知.
【解答】解:三角形中最大的角不能小于60°,如果小于60°,则三角形的内角和将小于180°,
又该三角形是锐角三角形,则最大角必须小于90°,故最大角的取值范围是60°≤α<90°.
故选:A.
4.下列判断正确的是( )
A.有两边和其中一边的对角对应相等的两个三角形全等
B.有两边对应相等,且有一角为30°的两个等腰三角形全等
C.有一角和一边对应相等的两个直角三角形全等
D.有两角和一边对应相等的两个三角形全等
【分析】判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL,对比选项进行分析.
【解答】解:A、只有两个三角形同为锐角三角形或者钝角三角形或者直角三角形时,才能成立;
B、30°角没有对应关系,不能成立;
C、如果这个角是直角,此时就不成立了;
D、符合全等三角形的判断方法:AAS或者ASA.
故选:D.
5.已知等腰三角形的一个角为75°,则其顶角为( )
A.30° B.75° C.105° D.30°或75°
【分析】因为等腰三角形的一个角为75°,没有明确说明是底角还是顶角,所以要分两种情况进行分析.
【解答】解:当75°角为底角时,顶角为180°﹣75°×2=30°;
75°角为顶角时,其底角==52.5°,
所以其顶角为30°或75°.
故选:D.
6.已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( )
A.4对 B.3对 C.2对 D.1对
【分析】解此题的关键是三角形全等的判定定理的准确应用.三角形全等的判定定理有:SSS,SAS,ASA,AAS.做题时要从已知入手由易到难,不重不漏.
【解答】解:∵CD⊥AB,BE⊥AC,
∴∠ADO=∠AEO=90°;
∵∠1=∠2,AO=AO,
∴△ADO≌△AEO(AAS).
∴AD=AE,
∵∠DAC=∠EAB,∠ADO=∠AEO,
∴△ADC≌△AEB(ASA).
∴AB=AC,
∵∠1=∠2,AO=AO,
∴△AOB≌△AOC(SAS).
∴∠B=∠C,
∵AD=AE,AB=AC,
∴DB=EC;
∵∠BOD=∠COE,
∴△BOD≌△COE(AAS).
故选:A.
二.填空题
7.如果在△ABC中,两边a=7cm,b=3cm,则c的取值范围是 4cm<c<10cm .
【分析】根据三角形的三边关系即可确定C的范围,即可求解.
【解答】解:C的范围是:(7﹣3)cm<c<(7+3)cm,
即4cm<c<10cm,
故答案为:4cm<c<10cm.
8.四条线段的长分别为5cm,6cm,8cm,13cm,以其中任意三条线段为边可以构成 2 个三角形.
【分析】首先每三条组合得到所有的情况,再进一步根据三角形的三边关系进行分析.
【解答】解:首先发现每三条可以组合为5、6、8;5、6、13;5、8、13;6、8、13;
再根据三角形的三边关系,可知能构成三角形的为:5、6、8和6、8、13.
因此可构成2个三角形.
故答案为:2.
9.一个等腰三角形的两边长分别是3cm和7cm,则它的周长是 17 cm.
【分析】等腰三角形两边的长为3cm和7cm,具体哪条是底边,哪条是腰没有明确说明,因此要分两种情况讨论.
【解答】解:①当腰是3cm,底边是7cm时:不满足三角形的三边关系,因此舍去.
②当底边是3cm,腰长是7cm时,能构成三角形,则其周长=3+7+7=17cm.
故答案为:17.
10.在Rt△ABC中,锐角∠A的平分线与锐角∠B的平分线相交于点D,则∠ADB= 135° .
【分析】根据三角形内角和定理求出∠CAB+∠CBA,再根据角平分线的定义求出∠DAB+∠DBA,然后利用三角形内角和定理列式进行计算即可得解.
【解答】解:在Rt△ABC中,∠CAB+∠CBA=180°﹣90°=90°,
∵锐角∠A的平分线与锐角∠B的平分线相交于点D,
∴∠DAB+∠DBA=(∠CAB+∠CBA)=×90°=45°,
在△ABD中,∠ADB=180°﹣(∠DAB+∠DBA)=180°﹣45°=135°.
故答案为:135°.
11.如图,∠A=∠D,AC=DF,则需要补充条件: AB=DE (写出一个即可),才能使△ABC≌△DEF.
【分析】要证明三角形全等,一定找出全等的三个条件,本题知道两个,只需添加一条边或一对角分别对应相等,结合图答案可得.
【解答】解:∵∠A=∠D,AC=DF,
若△ABC≌△DEF,
要添加AB=DE.
故填AB=DE.
12.已知:如图,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6cm,AC=8cm,则△ADE的周长为 14cm .
【分析】两直线平行,内错角相等,以及根据角平分线性质,可得△OBD、△EOC均为等腰三角形,由此把△AEF的周长转化为AC+AB.
【解答】解:∵DE∥BC
∴∠DOB=∠OBC,
又∵BO是∠ABC的角平分线,
∴∠DBO=∠OBC,
∴∠DBO=∠DOB,
∴BD=OD,
同理:OE=EC,
∴△ADE的周长=AD+OD+OE+AE=AD+BD+AE+EC=AB+AC=14cm.
故答案是:14cm.
13.如所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF∥EB;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有 ①③④ .
【分析】由∠E=∠F=90°,∠B=∠C,AE=AF,利用“AAS”得到△ABE与△ACF全等,根据全等三角形的对应边相等且对应角相等即可得到∠EAB与∠FAC相等,AE与AF相等,AB与AC相等,然后在等式∠EAB=∠FAC两边都减去∠MAN,得到∠EAM与∠FAN相等,然后再由∠E=∠F=90°,AE=AF,∠EAM=∠FAN,利用“ASA”得到△AEM与△AFN全等,利用全等三角形的对应边相等,对应角相等得到选项①和③正确;然后再∠C=∠B,AC=AB,∠CAN=∠BAM,利用“ASA”得到△ACN与△ABM全等,故选项④正确;若选项②正确,得到∠F与∠BDN相等,且都为90°,而∠BDN不一定为90°,故②错误.
【解答】解:在△ABE和△ACF中,
∠E=∠F=90°,AE=AF,∠B=∠C,
∴△ABE≌△ACF,
∴∠EAB=∠FAC,AE=AF,AB=AC,
∴∠EAB﹣∠MAN=∠FAC﹣∠NAM,即∠EAM=∠FAN,
在△AEM和△AFN中,
∠E=∠F=90°,AE=AF,∠EAM=∠FAN,
∴△AEM≌△AFN,
∴EM=FN,∠FAN=∠EAM,故选项①和③正确;
在△ACN和△ABM中,
∠C=∠B,AC=AB,∠CAN=∠BAM(公共角),
∴△ACN≌△ABM,故选项④正确;
若AF∥EB,∠F=∠BDN=90°,而∠BDN不一定为90°,故②错误,
则正确的选项有:①③④.
故答案为:①③④
14.如图,AD,AE分别是△ABC的角平分线和高线,且∠B=50°,∠C=70°,则∠EAD= 10° .
【分析】根据三角形的内角和等于180°求出∠BAC,再根据角平分线的定义求出∠BAD,根据直角三角形两锐角互余求出∠BAE,然后根据∠EAD=∠BAE﹣∠BAD代入数据进行计算即可得解.
【解答】解:∵∠B=50°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣70°=60°,
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=×60°=30°,
∵AE是△ABC的高线,
∴∠BAE=90°﹣∠B=90°﹣50°=40°,
∴∠EAD=∠BAE﹣∠BAD=40°﹣30°=10°.
故答案为:10°.
三.解答题
15.如图,已知△ABC≌△EFC,且CF=5,AC=12,∠EFC=50°,求∠E的度数和AB的长.
【分析】根据全等三角形性质求出AB=EF,AC=CE=12,∠ACB=∠ECF,求出∠ECF,根据勾股定理求出AB,根据三角形内角和定理求出∠E即可.
【解答】解:∵△ABC≌△EFC,
∴AB=EF,AC=CE=12,∠ACB=∠ECF,
∵∠ACB+∠ECF=180°,
∴∠ECF=90°,
∴∠E=180°﹣∠CFE﹣∠ECF=180°﹣50°﹣90°=40°,
由勾股定理得:AB=EF===13.
答:∠E的度数是40°,AB的长是13.
16.已知:如图,△ABC的∠B、∠C的平分线相交于点D,过D作MN∥BC交AB、AC分别于点M、N,
求证:BM+CN=MN.
【分析】根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据两直线平行,内错角相等可得∠6=∠2,∠3=∠5,然后求出∠1=∠6,∠4=∠5,根据等角对等边的性质可得BM=DM,CN=DN,然后列式求解即可得证.
【解答】证明:∵BD、CF平分∠ABC、∠ACB,
∴∠1=∠2,∠3=∠4,
∵MN∥BC,
∴∠6=∠2,∠3=∠5,
∴∠1=∠6,∠4=∠5,
∴BM=DM,CN=DN,
∴BM+CN=DM+DN,
即BM+CN=MN.
17.已知:如图,AB=DE,CD=FA,∠A=∠D,∠AFC=∠DCF,则BC=EF.你能说出它们相等的理由吗?
【分析】首先连接CE、BF,然后根据条件可证明△ABF≌△DEC,再根据全等三角形的性质可得∠3=∠4,BF=EC,然后证明△BCF≌△EFC可得BC=EF.
【解答】解:连接CE、BF,如图.
在△ABF和△DEC中,
∴△ABF≌△DEC(SAS).
∴∠3=∠4,BF=EC.
∵∠AFC=∠DCF,
∴∠AFC﹣∠3=∠DCF﹣∠4.
即∠1=∠2.
在△BCF和△EFC中,
∴△BCF≌△EFC(SAS).
∴BC=EF.
18.如图,点C在线段AB上,以AC和BC为边在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM,分别交CM,CN于点P,Q.△ACN和△MCB全等吗?说明理由.
【分析】根据等边三角形的性质得到∠ACM=∠BCN=60°,CA=CM,CN=CB,可得到∠MCN=60°,则∠ACN=∠BCM=120°,然后根据“SAS”可证明△ACN≌△MCB.
【解答】解:△ACN和△MCB全等;
理由:∵△ACM和△BCN都是等边三角形,
∴∠ACM=∠BCN=60°,CA=CM,CN=CB,
∴∠MCN=60°,
∴∠ACN=∠BCM=120°,
∵在△ACN和△MCB中,
,
∴△ACN≌△MCB(SAS).
19.我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等?
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
求证:△ABC≌△A1B1C1.
(请你将下列证明过程补充完整.)
证明:分别过点B,B1作BD⊥CA于D,
B1D1⊥C1A1于D1.
则∠BDC=∠B1D1C1=90°,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,
∴BD=B1D1.
(2)归纳与叙述:
由(1)可得到一个正确结论,请你写出这个结论.
【分析】本题考查的是全等三角形的判定,首先易证得△ADB≌△A1D1B1然后易证出△ABC≌△A1B1C1.
【解答】证明:(1)证明:分别过点B,B1作BD⊥CA于D,
B1D1⊥C1A1于D1.
则∠BDC=∠B1D1C1=90°,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,
∴BD=B1D1.
补充:∵AB=A1B1,∠ADB=∠A1D1B1=90°.
∴△ADB≌△A1D1B1(HL),
∴∠A=∠A1,
又∵∠C=∠C1,BC=B1C1,
在△ABC与△A1B1C1中,
∵,
∴△ABC≌△A1B1C1(AAS);
(2)解:若两三角形(△ABC、△A1B1C1)均为锐角三角形或均为直角三角形,则它们全等(AB=A1B1,BC=B1C1,∠C=∠C1,则△ABC≌△A1B1C1).
一.选择题
1.一个钝角三角形的三条角平分线所在的直线一定交于一点,这交点一定在( )
A.三角形内部 B.三角形的一边上
C.三角形外部 D.三角形的某个顶点上
2.下列各组线段中,能组成三角形的是( )
A.4,5,6 B.6,8,15 C.5,7,12 D.3,9,13
3.锐角三角形中,最大角α的取值范围是( )
A.60°≤α<90° B.60°<α<180° C.60°<α<90° D.0°<α<90°
4.下列判断正确的是( )
A.有两边和其中一边的对角对应相等的两个三角形全等
B.有两边对应相等,且有一角为30°的两个等腰三角形全等
C.有一角和一边对应相等的两个直角三角形全等
D.有两角和一边对应相等的两个三角形全等
5.已知等腰三角形的一个角为75°,则其顶角为( )
A.30° B.75° C.105° D.30°或75°
6.已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( )
A.4对 B.3对 C.2对 D.1对
二.填空题
7.如果在△ABC中,两边a=7cm,b=3cm,则c的取值范围是 .
8.四条线段的长分别为5cm,6cm,8cm,13cm,以其中任意三条线段为边可以构成 个三角形.
9.一个等腰三角形的两边长分别是3cm和7cm,则它的周长是 cm.
10.在Rt△ABC中,锐角∠A的平分线与锐角∠B的平分线相交于点D,则∠ADB= .
11.如图,∠A=∠D,AC=DF,则需要补充条件: (写出一个即可),才能使△ABC≌△DEF.
12.已知:如图,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6cm,AC=8cm,则△ADE的周长为 .
13.如所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF∥EB;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有 .
14.如图,AD,AE分别是△ABC的角平分线和高线,且∠B=50°,∠C=70°,则∠EAD= .
三.解答题
15.如图,已知△ABC≌△EFC,且CF=5,AC=12,∠EFC=50°,求∠E的度数和AB的长.
16.已知:如图,△ABC的∠B、∠C的平分线相交于点D,过D作MN∥BC交AB、AC分别于点M、N,
求证:BM+CN=MN.
17.已知:如图,AB=DE,CD=FA,∠A=∠D,∠AFC=∠DCF,则BC=EF.你能说出它们相等的理由吗?
18.如图,点C在线段AB上,以AC和BC为边在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM,分别交CM,CN于点P,Q.△ACN和△MCB全等吗?说明理由.
19.我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等?
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
求证:△ABC≌△A1B1C1.
(请你将下列证明过程补充完整.)
证明:分别过点B,B1作BD⊥CA于D,
B1D1⊥C1A1于D1.
则∠BDC=∠B1D1C1=90°,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,
∴BD=B1D1.
(2)归纳与叙述:
由(1)可得到一个正确结论,请你写出这个结论.
第4章 三角形
参考答案与试题解析
一.选择题
1.一个钝角三角形的三条角平分线所在的直线一定交于一点,这交点一定在( )
A.三角形内部 B.三角形的一边上
C.三角形外部 D.三角形的某个顶点上
【分析】根据三角形的高的性质即可判断.
【解答】解:一个钝角三角形的三条角平分线所在的直线一定交于一点,这交点一定在三角形的内部.
故选:A.
2.下列各组线段中,能组成三角形的是( )
A.4,5,6 B.6,8,15 C.5,7,12 D.3,9,13
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
【解答】解:A、4+5>6,5﹣4<6,能够组成三角形;
B、6+8<15,不能构成三角形;
C、5+7=12,不能构成三角形;
D、3+9<13,不能构成三角形.
故选:A.
3.锐角三角形中,最大角α的取值范围是( )
A.60°≤α<90° B.60°<α<180° C.60°<α<90° D.0°<α<90°
【分析】根据三角形的内角和是180°可知.
【解答】解:三角形中最大的角不能小于60°,如果小于60°,则三角形的内角和将小于180°,
又该三角形是锐角三角形,则最大角必须小于90°,故最大角的取值范围是60°≤α<90°.
故选:A.
4.下列判断正确的是( )
A.有两边和其中一边的对角对应相等的两个三角形全等
B.有两边对应相等,且有一角为30°的两个等腰三角形全等
C.有一角和一边对应相等的两个直角三角形全等
D.有两角和一边对应相等的两个三角形全等
【分析】判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL,对比选项进行分析.
【解答】解:A、只有两个三角形同为锐角三角形或者钝角三角形或者直角三角形时,才能成立;
B、30°角没有对应关系,不能成立;
C、如果这个角是直角,此时就不成立了;
D、符合全等三角形的判断方法:AAS或者ASA.
故选:D.
5.已知等腰三角形的一个角为75°,则其顶角为( )
A.30° B.75° C.105° D.30°或75°
【分析】因为等腰三角形的一个角为75°,没有明确说明是底角还是顶角,所以要分两种情况进行分析.
【解答】解:当75°角为底角时,顶角为180°﹣75°×2=30°;
75°角为顶角时,其底角==52.5°,
所以其顶角为30°或75°.
故选:D.
6.已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( )
A.4对 B.3对 C.2对 D.1对
【分析】解此题的关键是三角形全等的判定定理的准确应用.三角形全等的判定定理有:SSS,SAS,ASA,AAS.做题时要从已知入手由易到难,不重不漏.
【解答】解:∵CD⊥AB,BE⊥AC,
∴∠ADO=∠AEO=90°;
∵∠1=∠2,AO=AO,
∴△ADO≌△AEO(AAS).
∴AD=AE,
∵∠DAC=∠EAB,∠ADO=∠AEO,
∴△ADC≌△AEB(ASA).
∴AB=AC,
∵∠1=∠2,AO=AO,
∴△AOB≌△AOC(SAS).
∴∠B=∠C,
∵AD=AE,AB=AC,
∴DB=EC;
∵∠BOD=∠COE,
∴△BOD≌△COE(AAS).
故选:A.
二.填空题
7.如果在△ABC中,两边a=7cm,b=3cm,则c的取值范围是 4cm<c<10cm .
【分析】根据三角形的三边关系即可确定C的范围,即可求解.
【解答】解:C的范围是:(7﹣3)cm<c<(7+3)cm,
即4cm<c<10cm,
故答案为:4cm<c<10cm.
8.四条线段的长分别为5cm,6cm,8cm,13cm,以其中任意三条线段为边可以构成 2 个三角形.
【分析】首先每三条组合得到所有的情况,再进一步根据三角形的三边关系进行分析.
【解答】解:首先发现每三条可以组合为5、6、8;5、6、13;5、8、13;6、8、13;
再根据三角形的三边关系,可知能构成三角形的为:5、6、8和6、8、13.
因此可构成2个三角形.
故答案为:2.
9.一个等腰三角形的两边长分别是3cm和7cm,则它的周长是 17 cm.
【分析】等腰三角形两边的长为3cm和7cm,具体哪条是底边,哪条是腰没有明确说明,因此要分两种情况讨论.
【解答】解:①当腰是3cm,底边是7cm时:不满足三角形的三边关系,因此舍去.
②当底边是3cm,腰长是7cm时,能构成三角形,则其周长=3+7+7=17cm.
故答案为:17.
10.在Rt△ABC中,锐角∠A的平分线与锐角∠B的平分线相交于点D,则∠ADB= 135° .
【分析】根据三角形内角和定理求出∠CAB+∠CBA,再根据角平分线的定义求出∠DAB+∠DBA,然后利用三角形内角和定理列式进行计算即可得解.
【解答】解:在Rt△ABC中,∠CAB+∠CBA=180°﹣90°=90°,
∵锐角∠A的平分线与锐角∠B的平分线相交于点D,
∴∠DAB+∠DBA=(∠CAB+∠CBA)=×90°=45°,
在△ABD中,∠ADB=180°﹣(∠DAB+∠DBA)=180°﹣45°=135°.
故答案为:135°.
11.如图,∠A=∠D,AC=DF,则需要补充条件: AB=DE (写出一个即可),才能使△ABC≌△DEF.
【分析】要证明三角形全等,一定找出全等的三个条件,本题知道两个,只需添加一条边或一对角分别对应相等,结合图答案可得.
【解答】解:∵∠A=∠D,AC=DF,
若△ABC≌△DEF,
要添加AB=DE.
故填AB=DE.
12.已知:如图,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6cm,AC=8cm,则△ADE的周长为 14cm .
【分析】两直线平行,内错角相等,以及根据角平分线性质,可得△OBD、△EOC均为等腰三角形,由此把△AEF的周长转化为AC+AB.
【解答】解:∵DE∥BC
∴∠DOB=∠OBC,
又∵BO是∠ABC的角平分线,
∴∠DBO=∠OBC,
∴∠DBO=∠DOB,
∴BD=OD,
同理:OE=EC,
∴△ADE的周长=AD+OD+OE+AE=AD+BD+AE+EC=AB+AC=14cm.
故答案是:14cm.
13.如所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF∥EB;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有 ①③④ .
【分析】由∠E=∠F=90°,∠B=∠C,AE=AF,利用“AAS”得到△ABE与△ACF全等,根据全等三角形的对应边相等且对应角相等即可得到∠EAB与∠FAC相等,AE与AF相等,AB与AC相等,然后在等式∠EAB=∠FAC两边都减去∠MAN,得到∠EAM与∠FAN相等,然后再由∠E=∠F=90°,AE=AF,∠EAM=∠FAN,利用“ASA”得到△AEM与△AFN全等,利用全等三角形的对应边相等,对应角相等得到选项①和③正确;然后再∠C=∠B,AC=AB,∠CAN=∠BAM,利用“ASA”得到△ACN与△ABM全等,故选项④正确;若选项②正确,得到∠F与∠BDN相等,且都为90°,而∠BDN不一定为90°,故②错误.
【解答】解:在△ABE和△ACF中,
∠E=∠F=90°,AE=AF,∠B=∠C,
∴△ABE≌△ACF,
∴∠EAB=∠FAC,AE=AF,AB=AC,
∴∠EAB﹣∠MAN=∠FAC﹣∠NAM,即∠EAM=∠FAN,
在△AEM和△AFN中,
∠E=∠F=90°,AE=AF,∠EAM=∠FAN,
∴△AEM≌△AFN,
∴EM=FN,∠FAN=∠EAM,故选项①和③正确;
在△ACN和△ABM中,
∠C=∠B,AC=AB,∠CAN=∠BAM(公共角),
∴△ACN≌△ABM,故选项④正确;
若AF∥EB,∠F=∠BDN=90°,而∠BDN不一定为90°,故②错误,
则正确的选项有:①③④.
故答案为:①③④
14.如图,AD,AE分别是△ABC的角平分线和高线,且∠B=50°,∠C=70°,则∠EAD= 10° .
【分析】根据三角形的内角和等于180°求出∠BAC,再根据角平分线的定义求出∠BAD,根据直角三角形两锐角互余求出∠BAE,然后根据∠EAD=∠BAE﹣∠BAD代入数据进行计算即可得解.
【解答】解:∵∠B=50°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣70°=60°,
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=×60°=30°,
∵AE是△ABC的高线,
∴∠BAE=90°﹣∠B=90°﹣50°=40°,
∴∠EAD=∠BAE﹣∠BAD=40°﹣30°=10°.
故答案为:10°.
三.解答题
15.如图,已知△ABC≌△EFC,且CF=5,AC=12,∠EFC=50°,求∠E的度数和AB的长.
【分析】根据全等三角形性质求出AB=EF,AC=CE=12,∠ACB=∠ECF,求出∠ECF,根据勾股定理求出AB,根据三角形内角和定理求出∠E即可.
【解答】解:∵△ABC≌△EFC,
∴AB=EF,AC=CE=12,∠ACB=∠ECF,
∵∠ACB+∠ECF=180°,
∴∠ECF=90°,
∴∠E=180°﹣∠CFE﹣∠ECF=180°﹣50°﹣90°=40°,
由勾股定理得:AB=EF===13.
答:∠E的度数是40°,AB的长是13.
16.已知:如图,△ABC的∠B、∠C的平分线相交于点D,过D作MN∥BC交AB、AC分别于点M、N,
求证:BM+CN=MN.
【分析】根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据两直线平行,内错角相等可得∠6=∠2,∠3=∠5,然后求出∠1=∠6,∠4=∠5,根据等角对等边的性质可得BM=DM,CN=DN,然后列式求解即可得证.
【解答】证明:∵BD、CF平分∠ABC、∠ACB,
∴∠1=∠2,∠3=∠4,
∵MN∥BC,
∴∠6=∠2,∠3=∠5,
∴∠1=∠6,∠4=∠5,
∴BM=DM,CN=DN,
∴BM+CN=DM+DN,
即BM+CN=MN.
17.已知:如图,AB=DE,CD=FA,∠A=∠D,∠AFC=∠DCF,则BC=EF.你能说出它们相等的理由吗?
【分析】首先连接CE、BF,然后根据条件可证明△ABF≌△DEC,再根据全等三角形的性质可得∠3=∠4,BF=EC,然后证明△BCF≌△EFC可得BC=EF.
【解答】解:连接CE、BF,如图.
在△ABF和△DEC中,
∴△ABF≌△DEC(SAS).
∴∠3=∠4,BF=EC.
∵∠AFC=∠DCF,
∴∠AFC﹣∠3=∠DCF﹣∠4.
即∠1=∠2.
在△BCF和△EFC中,
∴△BCF≌△EFC(SAS).
∴BC=EF.
18.如图,点C在线段AB上,以AC和BC为边在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM,分别交CM,CN于点P,Q.△ACN和△MCB全等吗?说明理由.
【分析】根据等边三角形的性质得到∠ACM=∠BCN=60°,CA=CM,CN=CB,可得到∠MCN=60°,则∠ACN=∠BCM=120°,然后根据“SAS”可证明△ACN≌△MCB.
【解答】解:△ACN和△MCB全等;
理由:∵△ACM和△BCN都是等边三角形,
∴∠ACM=∠BCN=60°,CA=CM,CN=CB,
∴∠MCN=60°,
∴∠ACN=∠BCM=120°,
∵在△ACN和△MCB中,
,
∴△ACN≌△MCB(SAS).
19.我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等?
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
求证:△ABC≌△A1B1C1.
(请你将下列证明过程补充完整.)
证明:分别过点B,B1作BD⊥CA于D,
B1D1⊥C1A1于D1.
则∠BDC=∠B1D1C1=90°,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,
∴BD=B1D1.
(2)归纳与叙述:
由(1)可得到一个正确结论,请你写出这个结论.
【分析】本题考查的是全等三角形的判定,首先易证得△ADB≌△A1D1B1然后易证出△ABC≌△A1B1C1.
【解答】证明:(1)证明:分别过点B,B1作BD⊥CA于D,
B1D1⊥C1A1于D1.
则∠BDC=∠B1D1C1=90°,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,
∴BD=B1D1.
补充:∵AB=A1B1,∠ADB=∠A1D1B1=90°.
∴△ADB≌△A1D1B1(HL),
∴∠A=∠A1,
又∵∠C=∠C1,BC=B1C1,
在△ABC与△A1B1C1中,
∵,
∴△ABC≌△A1B1C1(AAS);
(2)解:若两三角形(△ABC、△A1B1C1)均为锐角三角形或均为直角三角形,则它们全等(AB=A1B1,BC=B1C1,∠C=∠C1,则△ABC≌△A1B1C1).
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
