小学数学北师大版六年级下册总复习图形与几何2-5 立体图形的表面积和体积 (32张PPT)课件
文档属性
| 名称 | 小学数学北师大版六年级下册总复习图形与几何2-5 立体图形的表面积和体积 (32张PPT)课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 929.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-21 09:48:36 | ||
图片预览









文档简介
六年级数学·下 新课标[北师]
总 复 习
2 图形与几何
随堂练习
课堂小结
作业设计
考点讲解
第5课时 立体图形的表面积和体积
考 点 讲 解
物体表面全部图形的面积之和就是物体的表面积。
①长方体:
S=(ab+ah+bh)×2
②正方体:
S=6a2
③圆柱:
S=2πrh+2πr2
立体图形的表面积
例1
做出下面这个化妆品盒至少需要多少平方厘米纸板?
5×5×6=150(平方厘米)
答:做出这个化妆品盒至少需要150平方厘米纸板。
一个游泳池从里面量长是80米,宽是60米,深是2.5米,在它的内壁四周和底部涂抹水泥,如果每平方米需要水泥6千克,那么一共需要水泥多少千克?
(80×2.5×2+60×2.5×2+80×60)×6
=(400+300+4800)×6
=5500×6
=33000(千克)
答:一共需要水泥33000千克。
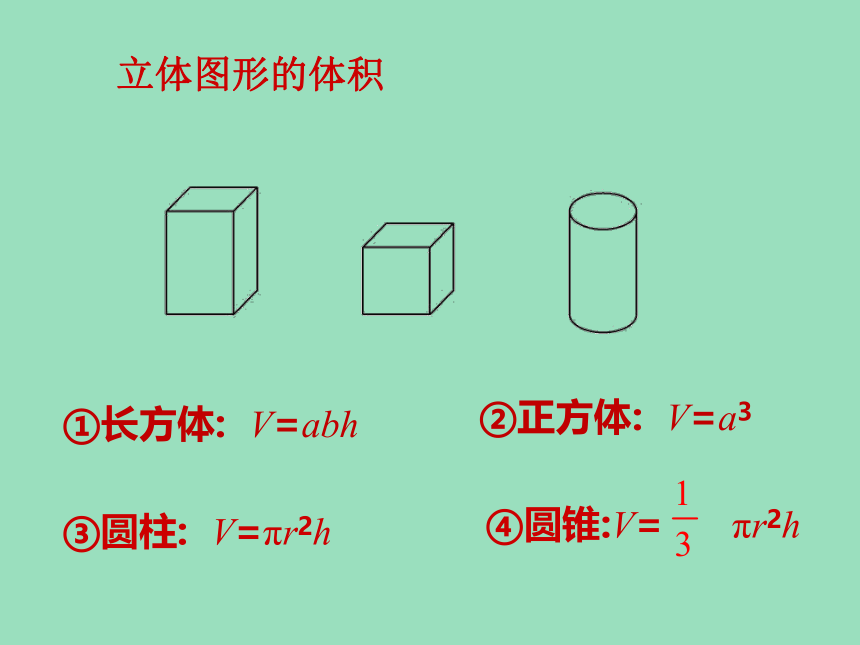
①长方体: V=abh
②正方体: V=a3
③圆柱: V=πr2h
④圆锥:V= πr2h
立体图形的体积
例2
把一个底面半径是2分米,高是12分米的圆柱形钢材重新熔铸成一个底面半径是4分米的圆锥,它的高是多少?
解法一
3.14×22×12×3÷(3.14×42)
=452.16÷50.24
=9(分米)
答:圆锥的高为9分米。
解法二
解:设圆锥的高为x分米。
答:圆锥的高为9分米。
把一个底面直径是4厘米,高是9厘米的圆锥形铁块完全沉浸在一个装满水的底面周长是25.12厘米的圆柱形容器中,当铁块从中取出后,容器中的水面下降了几厘米?
答:容器中的水面下降了0.75厘米。
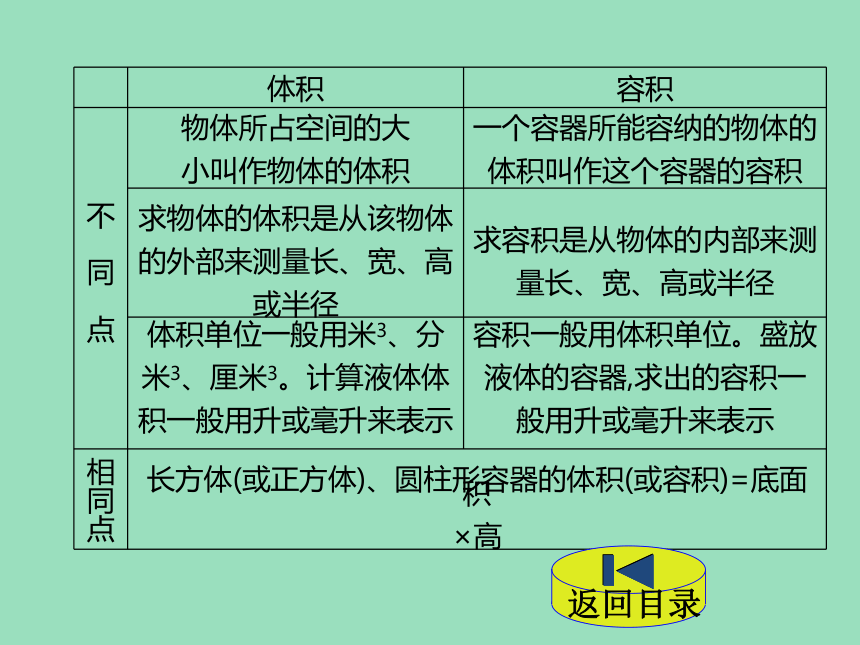
体积
容积
不
同
点
物体所占空间的大
小叫作物体的体积
一个容器所能容纳的物体的
体积叫作这个容器的容积
求物体的体积是从该物体
的外部来测量长、宽、高
或半径
求容积是从物体的内部来测
量长、宽、高或半径
体积单位一般用米3、分
米3、厘米3。计算液体体
积一般用升或毫升来表示
容积一般用体积单位。盛放
液体的容器,求出的容积一
般用升或毫升来表示
相
同
点
长方体(或正方体)、圆柱形容器的体积(或容积)=底面积
×高
返回目录
随堂练习
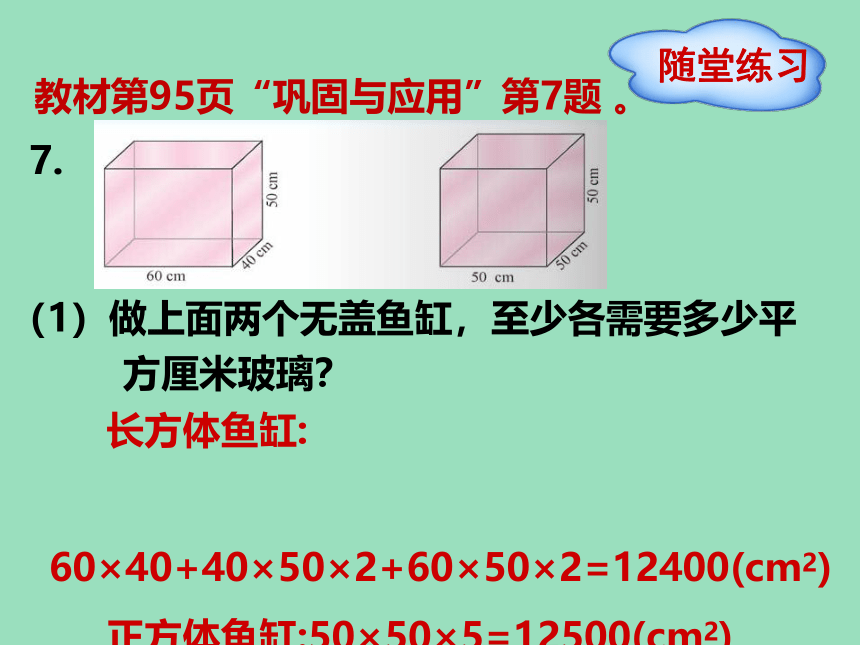
7.
教材第95页“巩固与应用”第7题 。
(1)做上面两个无盖鱼缸,至少各需要多少平
方厘米玻璃?
长方体鱼缸:
60×40+40×50×2+60×50×2=12400(cm2)
正方体鱼缸:50×50×5=12500(cm2)
返回目录
(2)哪个鱼缸盛水多?先猜一猜,再计算多了
多少升?
长方体鱼缸:60×40×50=120000(毫升)
120000毫升=120升
正方体鱼缸:50×50×50=125000(毫升)
125000毫升=125升
125-120=5(升)
答:正方体鱼缸盛水多,多5升。
课堂小结
谈谈你的收获吧!
返回目录
1.立体图形表面积的计算公式。
2.立体图形体积的计算公式。
作业设计
作业1
作业2
相信自己!
返回目录
作业1
11.用3个同样的小长方体,拼成一个大长方体,
可能有几种情况?它们的表面积各是多少?
教材第95页“巩固与应用”第11题 。
返回作业设计
长
宽
高
表面积
可能有3种情况,即每一种不同的面各重叠一次,情况如下:
3 cm
2 cm
3 cm
42 cm?
6 cm
1 cm
3 cm
54 cm?
9 cm
1 cm
2 cm
58 cm?
作业2
一、想一想,填一填
1.把两个棱长是3 cm的正方体拼成一个长方体,这
个长方体的表面积是( ),体积是( )。
2.一根圆柱形钢材的体积是882立方厘米,底面积
是42平方厘米,它的高是( )厘米。
3.把一根长是3米,底面半径是8厘米的圆柱形木
料锯成两段(平行于底面锯),表面积增加
( )平方厘米。
90 cm?
54 cm?
21
401.92
4.把一个圆柱体的侧面沿高线展开,得到一个正
方形,这个圆柱体的底面半径是0.6分米,它的高
是( )分米。
5.一个圆柱和一个圆锥等底等高,它们的体积之
和是124立方厘米,那么圆锥的体积是( )立
方厘米。
6.将某圆柱体的底面半径扩大到原来的2倍,高不
变,则体积扩大到原来的( )倍。
3.768
31
4
7.把12立方分米的水倒入一个长3分米、宽2分米、
高4分米的长方体玻璃缸内,水面距缸口有( )
分米。
8.一个正方体的棱长总和是60厘米,那么它的表
面积是( )平方厘米,体积是( )立方厘米。
2
150
125
9.把一根长48厘米的铁丝做成一个长方体的框架
(接头处不计)。已知长、宽、高的比为3∶2∶1,
则这个长方体最大一个面的面积是( )平方
厘米。
24
10.一个圆柱的侧面展开图是正方形,已知它的底
面周长是31.4厘米,则它的高是( )厘米。
31.4
二、我是聪明的小法官
1.两个圆柱的侧面积相等,它们的底面周长也一
定相等。 ( )
2.正方体、长方体、圆柱体都可以用它们各自
的底面积乘高求得体积。( )
3.圆柱体的底面半径扩大到原来的2倍,高也扩大
到原来的2倍,则侧面积扩大到原来的4倍。( )
×
√
√
4.把一段圆柱形的钢材削成一个最大的圆锥体,
削去部分的体积是原体积的 。 ( )
5.一个长方体的长、宽、高依次是a米、b米、h
米,如果高增加3米,那么新的长方体的体积比
原来的体积增加了3abh立方米。 ( )
×
×
三、选一选
1.一个正方体的棱长扩大到原来的3倍,那么它的
体积就扩大到原来的( )。
A.3倍 B.9倍 C.6倍 D.27倍
D
2.把一个圆柱形木料加工成一个和它等底等高
的圆锥体,则体积比原来减少了( )。
B
3.求一个圆柱形铁皮油桶能装多少油,就是计算
该油桶的( )。
A.侧面积
B.表面积
C.容积
C
四、求下列图形的表面积和体积(单位:厘米)
1.
8
3
4
表面积:(8×3+8×4+4×3)×2=136(平方厘米)
体积:8×3×4=96(立方厘米)
四、求下列图形的表面积和体积(单位:厘米)
2.
6
12
表面积:3.14×(6÷2)2×2+3.14×6×12=282.6(cm?)
体积:3.14×(6÷2)2×12=339.12(立方厘米)
五、解决问题
1.一个圆柱形水池,从内侧量底面直径是20米,深2米。
(1)在它的内侧面和底面抹水泥,抹水泥部分的面
积是多少?
20÷2=10(米)
3.14×102+3.14×20×2=439.6(平方米)
答:抹水泥部分的面积是439.6平方米。
1.一个圆柱形水池,从内侧量底面直径是20米,深2米。
(2)池内最多容水多少吨?(每立方米水约重1吨)
3.14×102×2×1=628(吨)
答:池内最多容水628吨。
2.一个圆锥形的沙堆,占地面积为15平方米,高2
米。把这堆沙铺在宽8米的路上,平均厚5厘米,
能铺路多少米?
答:能铺路25米。
3.从一个长方体上截下一个体积是18立方分米
的小长方体后,还剩下一个棱长是3分米的正方
体,则原来这个长方体的表面积是多少平方分米?
18÷(3×3)+3=5(分米)
5×3×4+3×3×2=78(平方分米)
答:原来这个长方体的表面积是78平方分米。
4.一个圆锥形容器,从内侧量圆锥底面半径是2分
米,高是5分米。明明用这个容器装满水,倒入一
个圆柱形水槽里,倒了9次才把水槽装满,求这个
水槽的容积有多大。
答:这个水槽的容积是188.4立方分米。
5.一个圆柱形铁皮水桶装满水,倒出20%后还剩24
升,桶的底面积是10平方分米,求桶高是多少。
24÷(1-20%)÷10=3(分米)
答:桶高是3分米。
返回作业设计
总 复 习
2 图形与几何
随堂练习
课堂小结
作业设计
考点讲解
第5课时 立体图形的表面积和体积
考 点 讲 解
物体表面全部图形的面积之和就是物体的表面积。
①长方体:
S=(ab+ah+bh)×2
②正方体:
S=6a2
③圆柱:
S=2πrh+2πr2
立体图形的表面积
例1
做出下面这个化妆品盒至少需要多少平方厘米纸板?
5×5×6=150(平方厘米)
答:做出这个化妆品盒至少需要150平方厘米纸板。
一个游泳池从里面量长是80米,宽是60米,深是2.5米,在它的内壁四周和底部涂抹水泥,如果每平方米需要水泥6千克,那么一共需要水泥多少千克?
(80×2.5×2+60×2.5×2+80×60)×6
=(400+300+4800)×6
=5500×6
=33000(千克)
答:一共需要水泥33000千克。
①长方体: V=abh
②正方体: V=a3
③圆柱: V=πr2h
④圆锥:V= πr2h
立体图形的体积
例2
把一个底面半径是2分米,高是12分米的圆柱形钢材重新熔铸成一个底面半径是4分米的圆锥,它的高是多少?
解法一
3.14×22×12×3÷(3.14×42)
=452.16÷50.24
=9(分米)
答:圆锥的高为9分米。
解法二
解:设圆锥的高为x分米。
答:圆锥的高为9分米。
把一个底面直径是4厘米,高是9厘米的圆锥形铁块完全沉浸在一个装满水的底面周长是25.12厘米的圆柱形容器中,当铁块从中取出后,容器中的水面下降了几厘米?
答:容器中的水面下降了0.75厘米。
体积
容积
不
同
点
物体所占空间的大
小叫作物体的体积
一个容器所能容纳的物体的
体积叫作这个容器的容积
求物体的体积是从该物体
的外部来测量长、宽、高
或半径
求容积是从物体的内部来测
量长、宽、高或半径
体积单位一般用米3、分
米3、厘米3。计算液体体
积一般用升或毫升来表示
容积一般用体积单位。盛放
液体的容器,求出的容积一
般用升或毫升来表示
相
同
点
长方体(或正方体)、圆柱形容器的体积(或容积)=底面积
×高
返回目录
随堂练习
7.
教材第95页“巩固与应用”第7题 。
(1)做上面两个无盖鱼缸,至少各需要多少平
方厘米玻璃?
长方体鱼缸:
60×40+40×50×2+60×50×2=12400(cm2)
正方体鱼缸:50×50×5=12500(cm2)
返回目录
(2)哪个鱼缸盛水多?先猜一猜,再计算多了
多少升?
长方体鱼缸:60×40×50=120000(毫升)
120000毫升=120升
正方体鱼缸:50×50×50=125000(毫升)
125000毫升=125升
125-120=5(升)
答:正方体鱼缸盛水多,多5升。
课堂小结
谈谈你的收获吧!
返回目录
1.立体图形表面积的计算公式。
2.立体图形体积的计算公式。
作业设计
作业1
作业2
相信自己!
返回目录
作业1
11.用3个同样的小长方体,拼成一个大长方体,
可能有几种情况?它们的表面积各是多少?
教材第95页“巩固与应用”第11题 。
返回作业设计
长
宽
高
表面积
可能有3种情况,即每一种不同的面各重叠一次,情况如下:
3 cm
2 cm
3 cm
42 cm?
6 cm
1 cm
3 cm
54 cm?
9 cm
1 cm
2 cm
58 cm?
作业2
一、想一想,填一填
1.把两个棱长是3 cm的正方体拼成一个长方体,这
个长方体的表面积是( ),体积是( )。
2.一根圆柱形钢材的体积是882立方厘米,底面积
是42平方厘米,它的高是( )厘米。
3.把一根长是3米,底面半径是8厘米的圆柱形木
料锯成两段(平行于底面锯),表面积增加
( )平方厘米。
90 cm?
54 cm?
21
401.92
4.把一个圆柱体的侧面沿高线展开,得到一个正
方形,这个圆柱体的底面半径是0.6分米,它的高
是( )分米。
5.一个圆柱和一个圆锥等底等高,它们的体积之
和是124立方厘米,那么圆锥的体积是( )立
方厘米。
6.将某圆柱体的底面半径扩大到原来的2倍,高不
变,则体积扩大到原来的( )倍。
3.768
31
4
7.把12立方分米的水倒入一个长3分米、宽2分米、
高4分米的长方体玻璃缸内,水面距缸口有( )
分米。
8.一个正方体的棱长总和是60厘米,那么它的表
面积是( )平方厘米,体积是( )立方厘米。
2
150
125
9.把一根长48厘米的铁丝做成一个长方体的框架
(接头处不计)。已知长、宽、高的比为3∶2∶1,
则这个长方体最大一个面的面积是( )平方
厘米。
24
10.一个圆柱的侧面展开图是正方形,已知它的底
面周长是31.4厘米,则它的高是( )厘米。
31.4
二、我是聪明的小法官
1.两个圆柱的侧面积相等,它们的底面周长也一
定相等。 ( )
2.正方体、长方体、圆柱体都可以用它们各自
的底面积乘高求得体积。( )
3.圆柱体的底面半径扩大到原来的2倍,高也扩大
到原来的2倍,则侧面积扩大到原来的4倍。( )
×
√
√
4.把一段圆柱形的钢材削成一个最大的圆锥体,
削去部分的体积是原体积的 。 ( )
5.一个长方体的长、宽、高依次是a米、b米、h
米,如果高增加3米,那么新的长方体的体积比
原来的体积增加了3abh立方米。 ( )
×
×
三、选一选
1.一个正方体的棱长扩大到原来的3倍,那么它的
体积就扩大到原来的( )。
A.3倍 B.9倍 C.6倍 D.27倍
D
2.把一个圆柱形木料加工成一个和它等底等高
的圆锥体,则体积比原来减少了( )。
B
3.求一个圆柱形铁皮油桶能装多少油,就是计算
该油桶的( )。
A.侧面积
B.表面积
C.容积
C
四、求下列图形的表面积和体积(单位:厘米)
1.
8
3
4
表面积:(8×3+8×4+4×3)×2=136(平方厘米)
体积:8×3×4=96(立方厘米)
四、求下列图形的表面积和体积(单位:厘米)
2.
6
12
表面积:3.14×(6÷2)2×2+3.14×6×12=282.6(cm?)
体积:3.14×(6÷2)2×12=339.12(立方厘米)
五、解决问题
1.一个圆柱形水池,从内侧量底面直径是20米,深2米。
(1)在它的内侧面和底面抹水泥,抹水泥部分的面
积是多少?
20÷2=10(米)
3.14×102+3.14×20×2=439.6(平方米)
答:抹水泥部分的面积是439.6平方米。
1.一个圆柱形水池,从内侧量底面直径是20米,深2米。
(2)池内最多容水多少吨?(每立方米水约重1吨)
3.14×102×2×1=628(吨)
答:池内最多容水628吨。
2.一个圆锥形的沙堆,占地面积为15平方米,高2
米。把这堆沙铺在宽8米的路上,平均厚5厘米,
能铺路多少米?
答:能铺路25米。
3.从一个长方体上截下一个体积是18立方分米
的小长方体后,还剩下一个棱长是3分米的正方
体,则原来这个长方体的表面积是多少平方分米?
18÷(3×3)+3=5(分米)
5×3×4+3×3×2=78(平方分米)
答:原来这个长方体的表面积是78平方分米。
4.一个圆锥形容器,从内侧量圆锥底面半径是2分
米,高是5分米。明明用这个容器装满水,倒入一
个圆柱形水槽里,倒了9次才把水槽装满,求这个
水槽的容积有多大。
答:这个水槽的容积是188.4立方分米。
5.一个圆柱形铁皮水桶装满水,倒出20%后还剩24
升,桶的底面积是10平方分米,求桶高是多少。
24÷(1-20%)÷10=3(分米)
答:桶高是3分米。
返回作业设计
