小学数学北师大版六年级下册总复习图形与几何2-2 平面图形 (30张PPT)课件
文档属性
| 名称 | 小学数学北师大版六年级下册总复习图形与几何2-2 平面图形 (30张PPT)课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-21 09:49:48 | ||
图片预览






文档简介
六年级数学·下 新课标[北师]
总 复 习
2 图形与几何
随堂练习
课堂小结
作业设计
考点讲解
第2课时 平面图形
考 点 讲 解
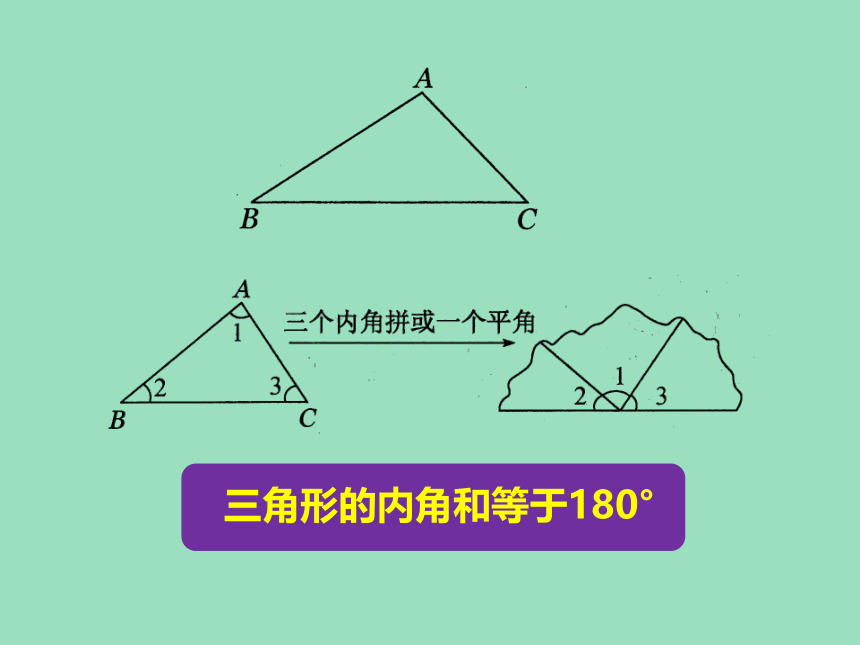
三角形的内角和等于180°
每组线段能不能围成一个三角形?
(1)5 cm,4 cm,3 cm
(2)3 cm,3 cm,6 cm
(3)3 cm,2 cm,7 cm
(1)组的三条线段能围成一个三角形,而(2)(3)组均不能围成三角形。
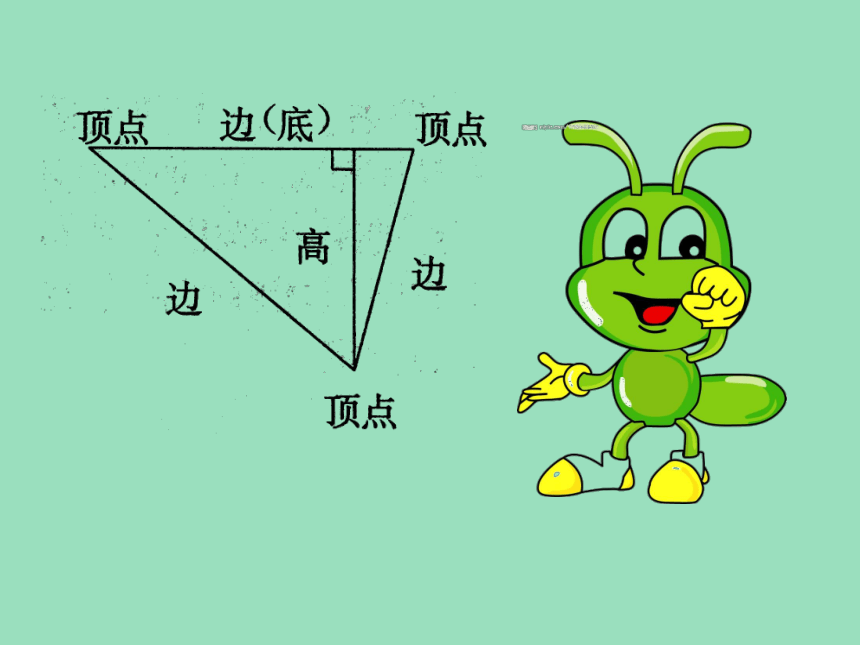
三角形的含义及各部分的名称:
(1)含义:由三条线段首尾顺次相接围成的图形叫
作三角形。
(2)各部分名称:围成三角形的每条线段叫作三角
形的边,两条线段的交点叫作三角形的顶点,从
三角形的一个顶点到它的对边作一条垂线,顶
点和垂足之间的线段叫作三角形的高,这条边
叫作三角形的底。
例1
有三组线段,能围成三角形的是哪一组?
第一组线段长:3厘米、5厘米、8厘米。
第二组线段长:7厘米、2厘米、8厘米。
第三组线段长:4厘米、6厘米、17厘米。
能围成三角形的是第二组线段。
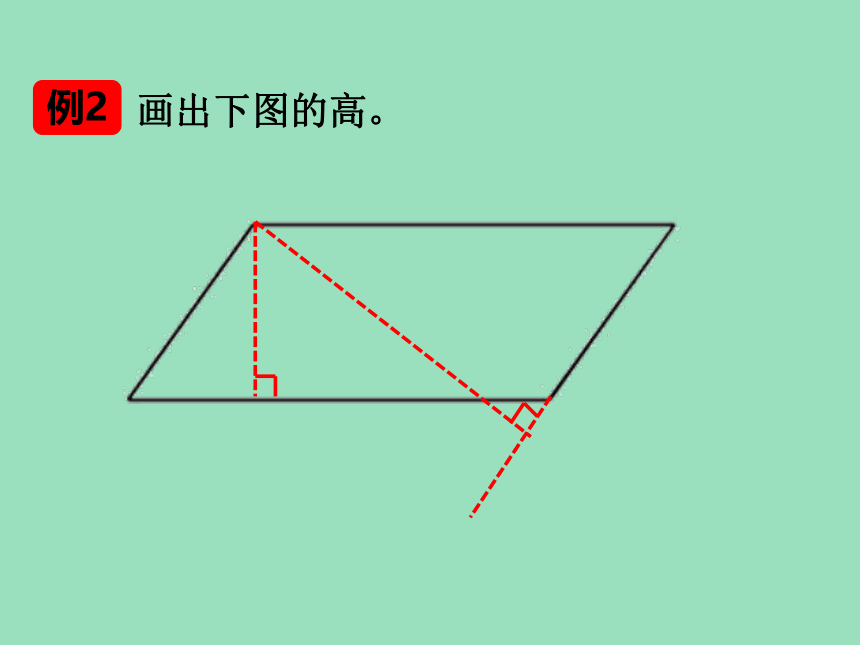
例2
画出下图的高。
(1)圆的有关定义:圆是一种封闭的曲线图形,圆
中心的一点叫作圆心,圆心到圆上任意一点
的线段叫作半径,通过圆心并且两端都在圆
上的线段叫作直径。
(2)在同圆或等圆中,直径等于半径的2倍。
(3)圆是轴对称图形,圆的直径所在的直线是它
的对称轴,圆有无数条对称轴。
例3
判断:圆的直径是半径的2倍。 ( )
×
返回目录
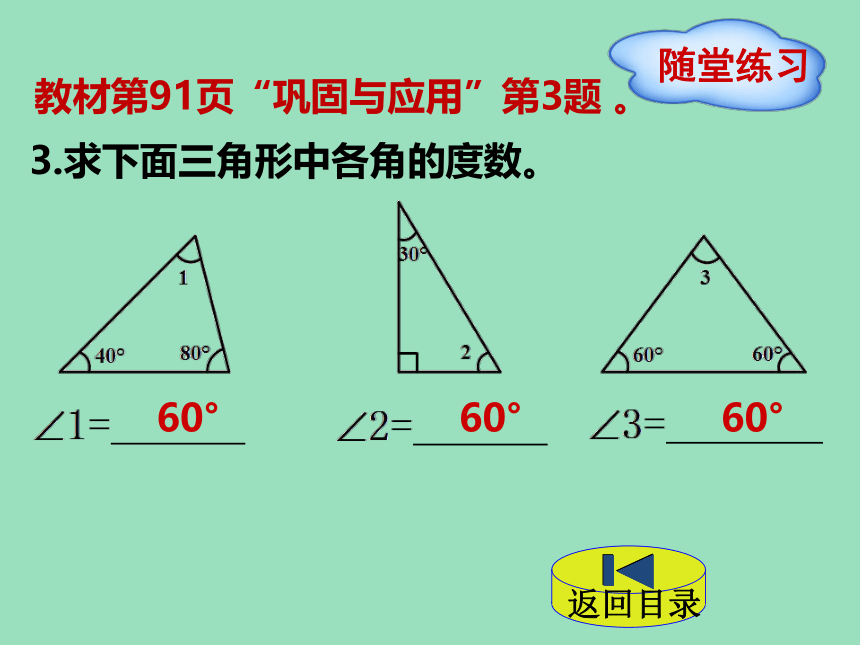
随堂练习
3.求下面三角形中各角的度数。
教材第91页“巩固与应用”第3题 。
60°
60°
60°
返回目录
课堂小结
谈谈你的收获吧!
返回目录
1.三角形的内角和。
2.三角形三条边之间的关系。
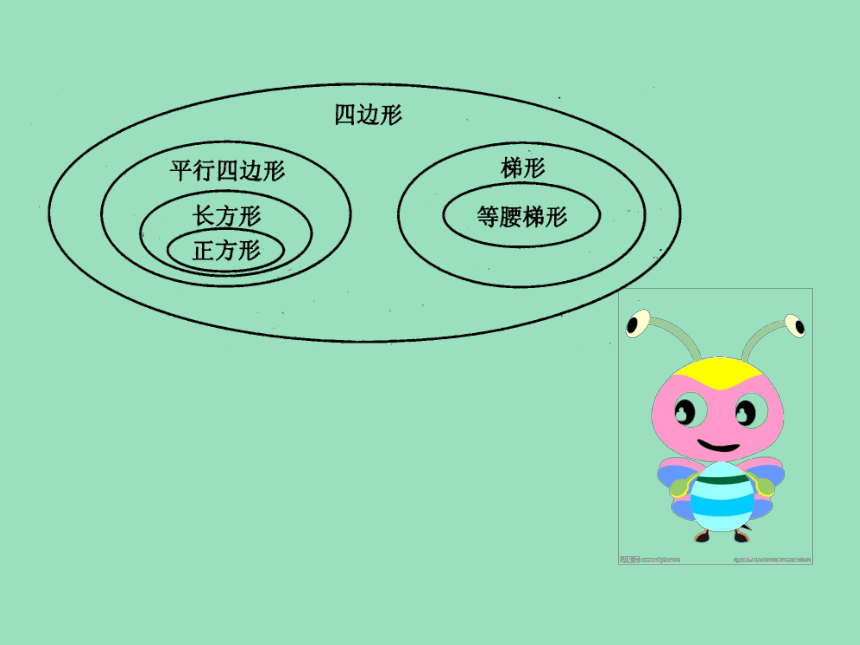
3. 四边形的知识。
4.圆的对称性。
作业设计
作业1
作业2
天天向上!
返回目录
作业1
4.在能围成三角形的一组线段下面画“√”。
(单位:cm)
教材第91页“巩固与应用”第4题 。
√
返回作业设计
作业2
一、想一想,填一填
1.一个等腰三角形的底角是60度,它的顶角是
( )度,它是一个( )三角形。
2.等腰梯形有( )条对称轴,长方形有( )条
对称轴,正方形有( )条对称轴。
3.圆心决定圆的( ),半径决定圆的( )。
60
等边
1
2
4
位置
大小
4.用圆规画一个直径是7厘米的圆,圆规两脚间
的距离应是( )厘米。
5.有一个三角形,若三个内角的度数之比是
2∶3∶4,则这个三角形是( )三角形;若三
个内角的度数之比是1∶2∶3,则这个三角形
是( )三角形。
6.三角形的内角和是( )度,等边三角形的
三个内角都是( )度。
3.5
锐角
直角
180
60
7.已知等腰三角形的顶角为70°,它的一个底角
是( ),这个三角形是( )三角形。
8.( )一组对边( )的四边形叫作梯形。
9.在同一个圆里,所有的半径都( ),所有的
( )也都相等,直径等于半径的( ),半
径等于直径的( )。
55°
只有
平行
相等
直径
锐角
2倍
一半
10.一个圆有( )条半径,( )条直径。
无数
无数
11.从一个长9 cm,宽6 cm的长方形纸上剪下一个
最大的圆,这个圆的直径是( )cm。
12.一个平行四边形的底是10 cm,底边上的高是
5 cm,和它等底等高的三角形的面积是
( )cm2。
6
25
二、我是聪明的小法官
1.有一组对边平行的四边形叫作平行四边形。
( )
×
2.一组对边相等,一组对边平行的四边形一定是
平行四边形。 ( )
×
3.平行四边形有两条对称轴。 ( )
×
4.等腰梯形、等腰三角形(非等边三角形)都只有
1条对称轴。 ( )
√
5.在一个三角形中,最少有两个内角是锐角。
( )
√
6.在下图中,阴影部分的面积甲比乙大。( )
甲
乙
×
7.等边三角形必定是锐角三角形。 ( )
√
8.底角是45°的等腰三角形,顶角是直角。( )
√
三、选一选
1.如果一个三角形最小的一个内角大于45°,那
么这个三角形一定是( )。
A.直角三角形 B.钝角三角形 C.锐角三角形
C
2.( )具有不易变形的特性。
A.三角形 B.长方形
C.平行四边形
A
3.下面各类图形中,( )有两条对称轴。
A.长方形 B.梯形
C.等边三角形
A
4.在一个等腰三角形中,已知两条边分别长10厘米
和5厘米,这个等腰三角形的周长是( )厘米。
A.20 B.25
C.20或25
B
5.如右图所示的等腰三角形的顶角是50°,则底
角是( )。
A.50° B.100°
C.65° D.130°
C
50°
四、画一画
1.画一个直径是1.6厘米的圆,再画出它的两条互
相垂直的对称轴。
2.在下图中画出三角形的任意一条高。
A
B
C
3.画一个长4厘米、宽2厘米的长方形。
4 cm
2 cm
五、解决问题
1.如图所示的是一个直角三角形,求出∠1和∠2
的度数。
1
2
3
140°
因为∠2+140°=180°,所以∠2=180°-140°=40°。
因为∠1+∠2+∠3=180°,所以
∠1=180°-90°-40°=50°。
2.如图所示,已知∠1=30°,∠2=18°,∠5=90°,
求∠3,∠4的度数。
1
2
3
4
5
因为∠1+∠5+∠3=180°,
∠1=30°,∠5=90°,
所以∠3=180°-30°-90°=60°。
因为∠4+∠1+∠5+∠2=180°,
∠1=30°,∠5=90°,∠2=18°,所以∠4=180°-∠1-∠2-∠5
=180°-30°-18°-90°
=42°
返回作业设计
总 复 习
2 图形与几何
随堂练习
课堂小结
作业设计
考点讲解
第2课时 平面图形
考 点 讲 解
三角形的内角和等于180°
每组线段能不能围成一个三角形?
(1)5 cm,4 cm,3 cm
(2)3 cm,3 cm,6 cm
(3)3 cm,2 cm,7 cm
(1)组的三条线段能围成一个三角形,而(2)(3)组均不能围成三角形。
三角形的含义及各部分的名称:
(1)含义:由三条线段首尾顺次相接围成的图形叫
作三角形。
(2)各部分名称:围成三角形的每条线段叫作三角
形的边,两条线段的交点叫作三角形的顶点,从
三角形的一个顶点到它的对边作一条垂线,顶
点和垂足之间的线段叫作三角形的高,这条边
叫作三角形的底。
例1
有三组线段,能围成三角形的是哪一组?
第一组线段长:3厘米、5厘米、8厘米。
第二组线段长:7厘米、2厘米、8厘米。
第三组线段长:4厘米、6厘米、17厘米。
能围成三角形的是第二组线段。
例2
画出下图的高。
(1)圆的有关定义:圆是一种封闭的曲线图形,圆
中心的一点叫作圆心,圆心到圆上任意一点
的线段叫作半径,通过圆心并且两端都在圆
上的线段叫作直径。
(2)在同圆或等圆中,直径等于半径的2倍。
(3)圆是轴对称图形,圆的直径所在的直线是它
的对称轴,圆有无数条对称轴。
例3
判断:圆的直径是半径的2倍。 ( )
×
返回目录
随堂练习
3.求下面三角形中各角的度数。
教材第91页“巩固与应用”第3题 。
60°
60°
60°
返回目录
课堂小结
谈谈你的收获吧!
返回目录
1.三角形的内角和。
2.三角形三条边之间的关系。
3. 四边形的知识。
4.圆的对称性。
作业设计
作业1
作业2
天天向上!
返回目录
作业1
4.在能围成三角形的一组线段下面画“√”。
(单位:cm)
教材第91页“巩固与应用”第4题 。
√
返回作业设计
作业2
一、想一想,填一填
1.一个等腰三角形的底角是60度,它的顶角是
( )度,它是一个( )三角形。
2.等腰梯形有( )条对称轴,长方形有( )条
对称轴,正方形有( )条对称轴。
3.圆心决定圆的( ),半径决定圆的( )。
60
等边
1
2
4
位置
大小
4.用圆规画一个直径是7厘米的圆,圆规两脚间
的距离应是( )厘米。
5.有一个三角形,若三个内角的度数之比是
2∶3∶4,则这个三角形是( )三角形;若三
个内角的度数之比是1∶2∶3,则这个三角形
是( )三角形。
6.三角形的内角和是( )度,等边三角形的
三个内角都是( )度。
3.5
锐角
直角
180
60
7.已知等腰三角形的顶角为70°,它的一个底角
是( ),这个三角形是( )三角形。
8.( )一组对边( )的四边形叫作梯形。
9.在同一个圆里,所有的半径都( ),所有的
( )也都相等,直径等于半径的( ),半
径等于直径的( )。
55°
只有
平行
相等
直径
锐角
2倍
一半
10.一个圆有( )条半径,( )条直径。
无数
无数
11.从一个长9 cm,宽6 cm的长方形纸上剪下一个
最大的圆,这个圆的直径是( )cm。
12.一个平行四边形的底是10 cm,底边上的高是
5 cm,和它等底等高的三角形的面积是
( )cm2。
6
25
二、我是聪明的小法官
1.有一组对边平行的四边形叫作平行四边形。
( )
×
2.一组对边相等,一组对边平行的四边形一定是
平行四边形。 ( )
×
3.平行四边形有两条对称轴。 ( )
×
4.等腰梯形、等腰三角形(非等边三角形)都只有
1条对称轴。 ( )
√
5.在一个三角形中,最少有两个内角是锐角。
( )
√
6.在下图中,阴影部分的面积甲比乙大。( )
甲
乙
×
7.等边三角形必定是锐角三角形。 ( )
√
8.底角是45°的等腰三角形,顶角是直角。( )
√
三、选一选
1.如果一个三角形最小的一个内角大于45°,那
么这个三角形一定是( )。
A.直角三角形 B.钝角三角形 C.锐角三角形
C
2.( )具有不易变形的特性。
A.三角形 B.长方形
C.平行四边形
A
3.下面各类图形中,( )有两条对称轴。
A.长方形 B.梯形
C.等边三角形
A
4.在一个等腰三角形中,已知两条边分别长10厘米
和5厘米,这个等腰三角形的周长是( )厘米。
A.20 B.25
C.20或25
B
5.如右图所示的等腰三角形的顶角是50°,则底
角是( )。
A.50° B.100°
C.65° D.130°
C
50°
四、画一画
1.画一个直径是1.6厘米的圆,再画出它的两条互
相垂直的对称轴。
2.在下图中画出三角形的任意一条高。
A
B
C
3.画一个长4厘米、宽2厘米的长方形。
4 cm
2 cm
五、解决问题
1.如图所示的是一个直角三角形,求出∠1和∠2
的度数。
1
2
3
140°
因为∠2+140°=180°,所以∠2=180°-140°=40°。
因为∠1+∠2+∠3=180°,所以
∠1=180°-90°-40°=50°。
2.如图所示,已知∠1=30°,∠2=18°,∠5=90°,
求∠3,∠4的度数。
1
2
3
4
5
因为∠1+∠5+∠3=180°,
∠1=30°,∠5=90°,
所以∠3=180°-30°-90°=60°。
因为∠4+∠1+∠5+∠2=180°,
∠1=30°,∠5=90°,∠2=18°,所以∠4=180°-∠1-∠2-∠5
=180°-30°-18°-90°
=42°
返回作业设计
