小学数学北师大版六年级下 正比例与反比例 课件(42张ppt)
文档属性
| 名称 | 小学数学北师大版六年级下 正比例与反比例 课件(42张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-21 10:29:26 | ||
图片预览









文档简介
六年级数学·下 新课标[北师]
总 复 习
1 数与代数
随堂练习
课堂小结
作业设计
考点讲解
第9课时 正比例与反比例
考 点 讲 解
两个数相除又叫作两个数的比。
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
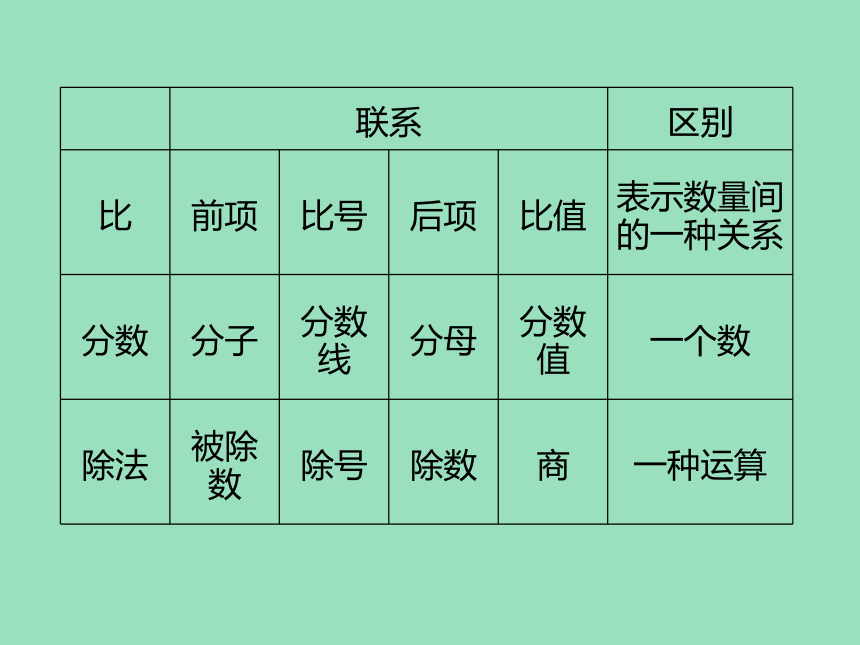
2.填一填,并说一说比、分数、除法之间的联系。
3
5
3
5
a
a
b
b
联系
区别
比
前项
比号
后项
比值
表示数量间
的一种关系
分数
分子
分数
线
分母
分数
值
一个数
除法
被除
数
除号
除数
商
一种运算
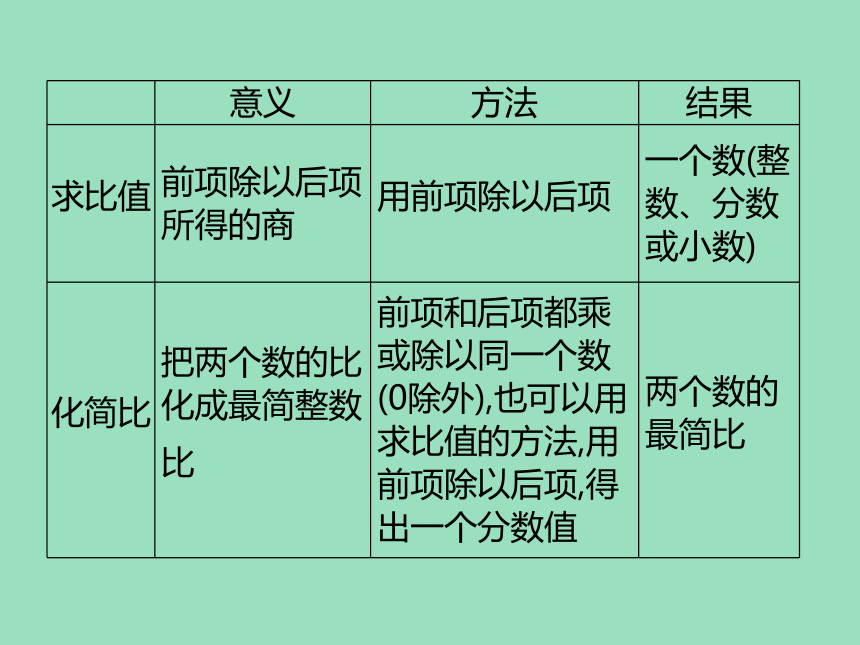
意义
方法
结果
求比值
前项除以后项
所得的商
用前项除以后项
一个数(整
数、分数
或小数)
化简比
把两个数的比
化成最简整数
比
前项和后项都乘
或除以同一个数
(0除外),也可以用
求比值的方法,用
前项除以后项,得
出一个分数值
两个数的
最简比
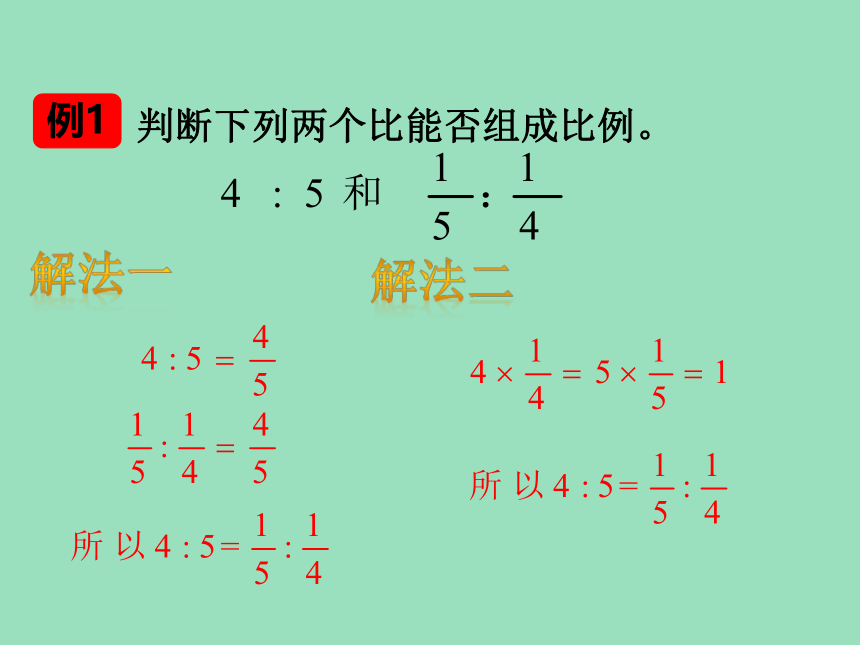
例1
判断下列两个比能否组成比例。
解法一
解法二
练习
在比例里,若两个内项互为倒数,其中一个外项是3,则另一个外项是几?
例2
填空。
4
12
75
练习
3
15
10
例3
某货场有750吨货物,分给两个运输队运到另一个货场。甲队有载重6吨的汽车6辆,乙队有载重8吨的汽车3辆,按两个队的运输能力分配,只运一次,甲、乙两队各应运货多少吨?
解法一
(6×6)∶(8×3)=36∶24=3∶2
3+2=5
答:甲队应运货物450吨,乙队应运货物300吨。
解法二
(6×6)∶(8×3)=3∶2
甲队:750÷(3+2)×3=450(吨)
乙队:750÷(3+2)×2=300(吨)
答:甲队应运货物450吨,乙队应运货物300吨。
解法三
解:设甲队应运货物x吨。
x∶(750-x)=(6×6)∶(8×3)
x∶(750-x)=3∶2
5x=2250
x=450
750-450=300(吨)
答:甲队应运货物450吨,乙队应运货物300吨。
3.(1)说说图中的比例尺
1:6000表示什么意思。
图中的1 cm是实际距离的6000 cm,即60 m。
(2)240 m长的马路在图上应画多长?
240 m=24000 cm
答:在图上应画4 cm。
例4
在比例尺是1∶8000000的地图上,量得济南与青岛的距离约是4厘米,济南到青岛的实际距离大约是多少千米?
解:设实际距离大约是x厘米。
32000000厘米=320千米
答:济南到青岛的实际距离大约是320千米。
练习
篮球场长28 m,宽15 m,把它画在比例尺是 的图纸上,面积是多少?
解:设长应画x m,宽应画y m。
0.056 m=5.6 cm
0.03 m=3 cm
5.6×3=16.8(cm2)
答:面积是16.8 cm2。
5.一辆汽车在高速路上行驶,速度保持在100千
米/时。说一说汽车行驶的路程随时间变化的
情况,并用多种方式表示这两个量之间的关系。
(1)可以列表。
时间/时
1
2
3
4
5
…
路程/km
100
…
200
300
400
500
(2)可以画图。
(3)可以用式子表示。
如果用t表示汽车行驶的时间,s表示汽车行驶的路程,那么 。
s=100t
(4)判断路程与时间是否成正比例,说说你是
怎么想的。
成正比例,因为路程与时间是相关联的量,它们的比值一定。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,那么这两种量就是成正比例的量,它们的关系叫作正比例关系。
y
x
=k
(一定)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,那么这两种量就叫作成反比例的量,它们的关系叫作反比例关系。
xy=k(一定)
判断正、反比例的方法:
一找、二看、三判断。即:(1)找变量:分析数量关系,确定哪两种量是相关联的量。(2)看定量:分析这两种相关联的量,它们之间的关系是商一定,还是积一定。(3)判断:如果商一定,就成正比例;如果积一定,就成反比例;如果商和积都不是定量,就不成正比例,也不成反比例。
例5
判断下面每题中的两种量是否成比例,成什么比例?
(1)圆的周长和半径。
(2)圆的面积和半径。
(3)长方形的周长一定,长和宽。
(4)长方形的面积一定,长和宽。
圆的周长和半径成比例,成正比例。
圆的面积和半径不成比例。
长方形的周长一定,长和宽不成比例。
长方形的面积一定,长和宽成比例,成反比例。
例6
买笔记本的数量和总钱数的关系如下表:
数量/本
0
1
2
3
4
5
6
7
…
总钱数/元
0
1.5
3
…
(1)将表格补充完整,根据
表中的数据,在图中描
点再顺次连接并延长。
4.5
6
7.5
9
10.5
(2)哪个量没变?数量和总钱数之间成什么比例?
单价不变,数量和总钱数之间成正比例。
(3)从图中可以看出,如果买9本笔记本,需要多少
元钱?
单价=1.5÷1=1.5(元)
1.5×9=13.5(元)
返回目录
随堂练习
1.填一填。
教材第84页“巩固与应用”第1题 。
(1)两个正方形的边长比是1:3,周长比是
( ),面积比是( )。
(2)9元可以买2 kg鸡蛋,总价与数量的比是
( ),比值是( )。
(3)汽车3时行150 km,路程与时间的比是
( ),比值是( )。
1:3
1:9
9:2
4.5
150:3
50
2.化简。
教材第84页“巩固与应用”第2题 。
5.判断下面每题中的两个量是否成正比例或反比例。
教材第84页“巩固与应用”第5题 。
返回目录
(1)一捆100 m长的电线,用去的长度与剩下的长度。
(2)三角形的面积一定,它的底和高。
(3)一个数与它的倒数。
既不成正比例,也不成反比例
反比例
反比例
课堂小结
谈谈你的收获吧!
返回目录
1.比、比例的意义。
2.正比例、反比例的意义。
3. 解决生活中的实际问题。
作业设计
作业1
作业2
要细心哟!
返回目录
作业1
6.下面表格中的两个量是否成正比例或反比例?
为什么?
教材第84页“巩固与应用”第6题 。
(1)输液时,一小瓶葡萄糖均匀滴落,每分滴
数与所需时间的关系如下。
反比例
(2)妙想的身高与体重的关系如下。
不成比例
(3)体积一定,圆柱体的底面积与高的关系如下。
反比例
返回作业设计
7.磁悬浮列车匀速行驶时,路程与时间的关系如下。
教材第84页“巩固与应用”第7题 。
(1)图中的点A表示时间为1
分时,磁悬浮列车驶过
的路程为7km。请你试着
描出其他各点。
(2)连接各点,它们在一条
直线上吗?
(3)列车运行2.5分时,行驶
的路程是多少?
在一条直线上。
列车运行2.5分时,行驶的路程为17.5 km。
作业2
一、想一想,填一填
1.圆的周长和半径成( )比例。
2.车轮的直径一定,车轮所行驶的路程和车轮转
动的圈数成( )比例。
正
正
(a≠0)中,( )一定时,( )和( )
成反比例;x一定时,y和a成( )比例。
y
a
x
正
4.出油率一定,黄豆的质量和所出的油的质量成
( )比例。
正
5.圆柱体的底面半径一定,它的高和体积成( )
比例。
正
6.运送货物总量一定,已运的货物和剩下的货物
( )正比例或反比例。
不成
7.正方形的边长和面积( )正比例或反比例。
不成
8.工作时间一定,工作效率和工作总量成( )
比例。
正
9.0.5∶ 的比值是( ),化简比是( )。
4
4:1
10.8∶x=4∶2,x=( )。
4
二、选一选
1.如果 x= y(x,y非零),那么x和y( )。
A.成正比例 B.成反比例
C.以上都不对
A
2.当a一定且不为0时,表示y和x成反比例的式子
是( )。
D
3.下列说法不正确的是( )。
A.梯形的面积一定,上、下底的和与高成反比例
B.长方形的周长一定,它的长和宽不成正比例或
反比例
C.订阅《求知报》的份数和总钱数成正比例(每
份《求知报》的钱数一定)
D.因为圆的周长C=πd,所以π与d成反比例
E.实际距离一定,图上距离和比例尺成正比例
D
三、观察下面两个表,完成问题
路程/千米
时间/小时
30
1
60
2
90
3
120
4
150
5
180
6
速度/(千米/时)
时间/小时
120
1
60
2
40
3
30
4
24
5
20
6
1.根据两表中给出的数据,分别在下面两图中
找出各点,并顺次连接各点。
0
1
2
3
4
5
6
时间
/小时
30
60
90
120
150
180
路程/千米
0
1
2
3
4
5
6
时间
/小时
20
40
60
80
100
120
速度/(千米/时)
①
②
2.在图①中找一找,行驶100千米,大约需要
( )小时。
3.3
3.在图②中找一找,如果想要2.5小时走完全程,
那么大约每小时行驶( )千米。
48
4.图①中的两种量成什么比例?图②中的两种
量呢?
图①:正比例
图②:反比例
5.在两个图中,你发现了什么?
从图①可看出,各点在一条直线上,路程随着时间的增加而增加,路程越长,需要的时间越长;
从图②可看出,各点在一条曲线上,速度随着时间的增加而减小。
返回作业设计
总 复 习
1 数与代数
随堂练习
课堂小结
作业设计
考点讲解
第9课时 正比例与反比例
考 点 讲 解
两个数相除又叫作两个数的比。
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
2.填一填,并说一说比、分数、除法之间的联系。
3
5
3
5
a
a
b
b
联系
区别
比
前项
比号
后项
比值
表示数量间
的一种关系
分数
分子
分数
线
分母
分数
值
一个数
除法
被除
数
除号
除数
商
一种运算
意义
方法
结果
求比值
前项除以后项
所得的商
用前项除以后项
一个数(整
数、分数
或小数)
化简比
把两个数的比
化成最简整数
比
前项和后项都乘
或除以同一个数
(0除外),也可以用
求比值的方法,用
前项除以后项,得
出一个分数值
两个数的
最简比
例1
判断下列两个比能否组成比例。
解法一
解法二
练习
在比例里,若两个内项互为倒数,其中一个外项是3,则另一个外项是几?
例2
填空。
4
12
75
练习
3
15
10
例3
某货场有750吨货物,分给两个运输队运到另一个货场。甲队有载重6吨的汽车6辆,乙队有载重8吨的汽车3辆,按两个队的运输能力分配,只运一次,甲、乙两队各应运货多少吨?
解法一
(6×6)∶(8×3)=36∶24=3∶2
3+2=5
答:甲队应运货物450吨,乙队应运货物300吨。
解法二
(6×6)∶(8×3)=3∶2
甲队:750÷(3+2)×3=450(吨)
乙队:750÷(3+2)×2=300(吨)
答:甲队应运货物450吨,乙队应运货物300吨。
解法三
解:设甲队应运货物x吨。
x∶(750-x)=(6×6)∶(8×3)
x∶(750-x)=3∶2
5x=2250
x=450
750-450=300(吨)
答:甲队应运货物450吨,乙队应运货物300吨。
3.(1)说说图中的比例尺
1:6000表示什么意思。
图中的1 cm是实际距离的6000 cm,即60 m。
(2)240 m长的马路在图上应画多长?
240 m=24000 cm
答:在图上应画4 cm。
例4
在比例尺是1∶8000000的地图上,量得济南与青岛的距离约是4厘米,济南到青岛的实际距离大约是多少千米?
解:设实际距离大约是x厘米。
32000000厘米=320千米
答:济南到青岛的实际距离大约是320千米。
练习
篮球场长28 m,宽15 m,把它画在比例尺是 的图纸上,面积是多少?
解:设长应画x m,宽应画y m。
0.056 m=5.6 cm
0.03 m=3 cm
5.6×3=16.8(cm2)
答:面积是16.8 cm2。
5.一辆汽车在高速路上行驶,速度保持在100千
米/时。说一说汽车行驶的路程随时间变化的
情况,并用多种方式表示这两个量之间的关系。
(1)可以列表。
时间/时
1
2
3
4
5
…
路程/km
100
…
200
300
400
500
(2)可以画图。
(3)可以用式子表示。
如果用t表示汽车行驶的时间,s表示汽车行驶的路程,那么 。
s=100t
(4)判断路程与时间是否成正比例,说说你是
怎么想的。
成正比例,因为路程与时间是相关联的量,它们的比值一定。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,那么这两种量就是成正比例的量,它们的关系叫作正比例关系。
y
x
=k
(一定)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,那么这两种量就叫作成反比例的量,它们的关系叫作反比例关系。
xy=k(一定)
判断正、反比例的方法:
一找、二看、三判断。即:(1)找变量:分析数量关系,确定哪两种量是相关联的量。(2)看定量:分析这两种相关联的量,它们之间的关系是商一定,还是积一定。(3)判断:如果商一定,就成正比例;如果积一定,就成反比例;如果商和积都不是定量,就不成正比例,也不成反比例。
例5
判断下面每题中的两种量是否成比例,成什么比例?
(1)圆的周长和半径。
(2)圆的面积和半径。
(3)长方形的周长一定,长和宽。
(4)长方形的面积一定,长和宽。
圆的周长和半径成比例,成正比例。
圆的面积和半径不成比例。
长方形的周长一定,长和宽不成比例。
长方形的面积一定,长和宽成比例,成反比例。
例6
买笔记本的数量和总钱数的关系如下表:
数量/本
0
1
2
3
4
5
6
7
…
总钱数/元
0
1.5
3
…
(1)将表格补充完整,根据
表中的数据,在图中描
点再顺次连接并延长。
4.5
6
7.5
9
10.5
(2)哪个量没变?数量和总钱数之间成什么比例?
单价不变,数量和总钱数之间成正比例。
(3)从图中可以看出,如果买9本笔记本,需要多少
元钱?
单价=1.5÷1=1.5(元)
1.5×9=13.5(元)
返回目录
随堂练习
1.填一填。
教材第84页“巩固与应用”第1题 。
(1)两个正方形的边长比是1:3,周长比是
( ),面积比是( )。
(2)9元可以买2 kg鸡蛋,总价与数量的比是
( ),比值是( )。
(3)汽车3时行150 km,路程与时间的比是
( ),比值是( )。
1:3
1:9
9:2
4.5
150:3
50
2.化简。
教材第84页“巩固与应用”第2题 。
5.判断下面每题中的两个量是否成正比例或反比例。
教材第84页“巩固与应用”第5题 。
返回目录
(1)一捆100 m长的电线,用去的长度与剩下的长度。
(2)三角形的面积一定,它的底和高。
(3)一个数与它的倒数。
既不成正比例,也不成反比例
反比例
反比例
课堂小结
谈谈你的收获吧!
返回目录
1.比、比例的意义。
2.正比例、反比例的意义。
3. 解决生活中的实际问题。
作业设计
作业1
作业2
要细心哟!
返回目录
作业1
6.下面表格中的两个量是否成正比例或反比例?
为什么?
教材第84页“巩固与应用”第6题 。
(1)输液时,一小瓶葡萄糖均匀滴落,每分滴
数与所需时间的关系如下。
反比例
(2)妙想的身高与体重的关系如下。
不成比例
(3)体积一定,圆柱体的底面积与高的关系如下。
反比例
返回作业设计
7.磁悬浮列车匀速行驶时,路程与时间的关系如下。
教材第84页“巩固与应用”第7题 。
(1)图中的点A表示时间为1
分时,磁悬浮列车驶过
的路程为7km。请你试着
描出其他各点。
(2)连接各点,它们在一条
直线上吗?
(3)列车运行2.5分时,行驶
的路程是多少?
在一条直线上。
列车运行2.5分时,行驶的路程为17.5 km。
作业2
一、想一想,填一填
1.圆的周长和半径成( )比例。
2.车轮的直径一定,车轮所行驶的路程和车轮转
动的圈数成( )比例。
正
正
(a≠0)中,( )一定时,( )和( )
成反比例;x一定时,y和a成( )比例。
y
a
x
正
4.出油率一定,黄豆的质量和所出的油的质量成
( )比例。
正
5.圆柱体的底面半径一定,它的高和体积成( )
比例。
正
6.运送货物总量一定,已运的货物和剩下的货物
( )正比例或反比例。
不成
7.正方形的边长和面积( )正比例或反比例。
不成
8.工作时间一定,工作效率和工作总量成( )
比例。
正
9.0.5∶ 的比值是( ),化简比是( )。
4
4:1
10.8∶x=4∶2,x=( )。
4
二、选一选
1.如果 x= y(x,y非零),那么x和y( )。
A.成正比例 B.成反比例
C.以上都不对
A
2.当a一定且不为0时,表示y和x成反比例的式子
是( )。
D
3.下列说法不正确的是( )。
A.梯形的面积一定,上、下底的和与高成反比例
B.长方形的周长一定,它的长和宽不成正比例或
反比例
C.订阅《求知报》的份数和总钱数成正比例(每
份《求知报》的钱数一定)
D.因为圆的周长C=πd,所以π与d成反比例
E.实际距离一定,图上距离和比例尺成正比例
D
三、观察下面两个表,完成问题
路程/千米
时间/小时
30
1
60
2
90
3
120
4
150
5
180
6
速度/(千米/时)
时间/小时
120
1
60
2
40
3
30
4
24
5
20
6
1.根据两表中给出的数据,分别在下面两图中
找出各点,并顺次连接各点。
0
1
2
3
4
5
6
时间
/小时
30
60
90
120
150
180
路程/千米
0
1
2
3
4
5
6
时间
/小时
20
40
60
80
100
120
速度/(千米/时)
①
②
2.在图①中找一找,行驶100千米,大约需要
( )小时。
3.3
3.在图②中找一找,如果想要2.5小时走完全程,
那么大约每小时行驶( )千米。
48
4.图①中的两种量成什么比例?图②中的两种
量呢?
图①:正比例
图②:反比例
5.在两个图中,你发现了什么?
从图①可看出,各点在一条直线上,路程随着时间的增加而增加,路程越长,需要的时间越长;
从图②可看出,各点在一条曲线上,速度随着时间的增加而减小。
返回作业设计
