北师大版 六年级数学下册3-1 圆柱体积的计算方法 课件(23页PPT)
文档属性
| 名称 | 北师大版 六年级数学下册3-1 圆柱体积的计算方法 课件(23页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-21 00:00:00 | ||
图片预览





文档简介
第1单元 圆柱与圆锥
六年级数学·下 新课标[北师]
3 圆柱的体积
学习新知
随堂练习
作业设计
复习准备
第1课时 圆柱体积的计算方法
复 习 准 备
1.用字母表示下面的公式。
返回目录
S圆= ,V长方体= ,V正方体= 。?
πr2
abh
a?
2.求正方体和长方体的体积,可以用一个统一
的计算公式来表示,这个计算公式是什么?
V=Sh
学 习 新 知
长方体体积=长×宽×高
正方体体积=边长?
长(正)方体的体积=底面积×高
老朋友
新朋友
一个圆柱体所占空间的大小叫作圆柱的体积。
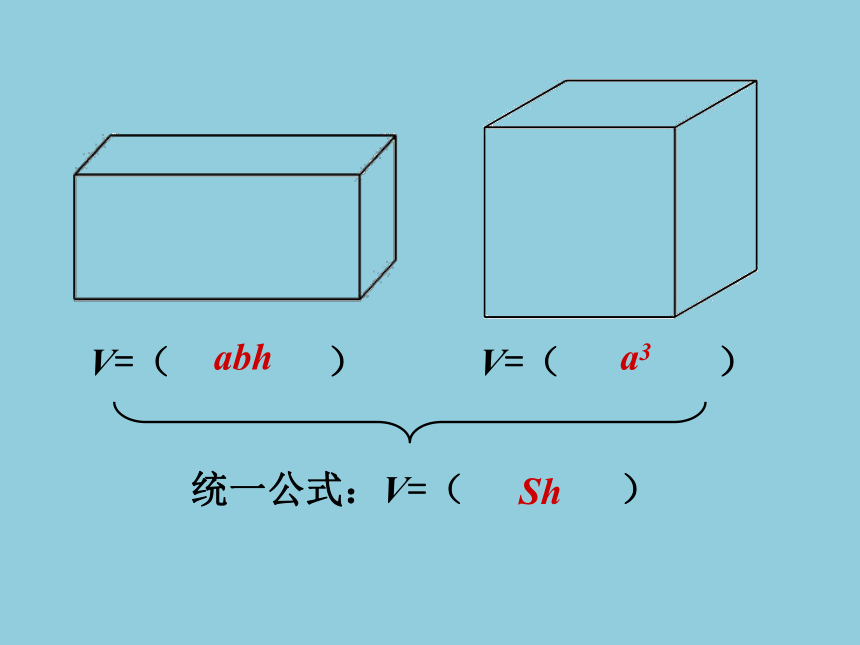
V=( )
V=( )
统一公式:V=( )
abh
a3
Sh
从叠硬币来看,用“底面积×高”能计算出圆柱的体积。
问题
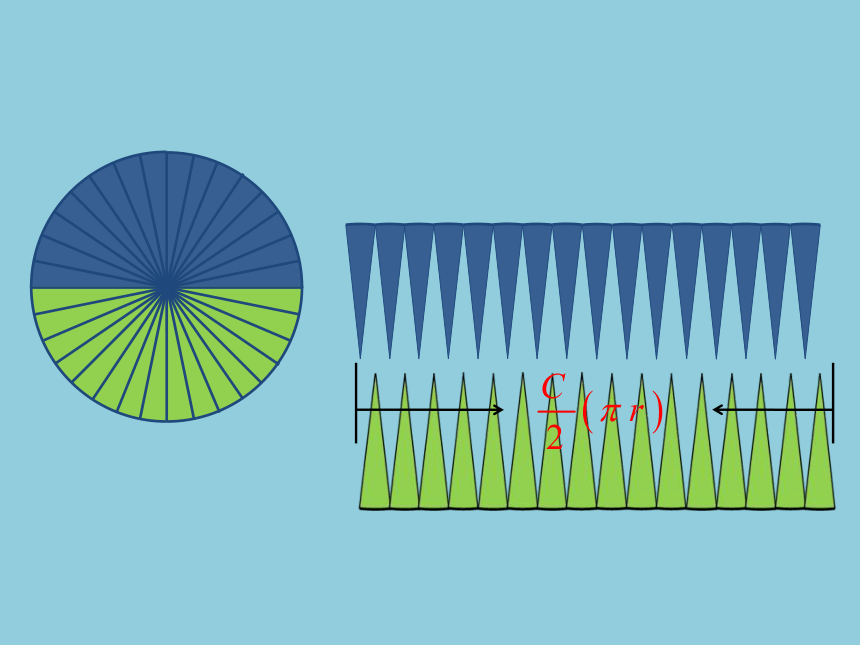
a.你准备把圆柱体转化成什么立体图形?
b.你是怎样转化成这个立体图形的?
c.转化以后的立体图形和圆柱体之间有什么
关系?
底面积相等
圆柱的高于长方体的高相等
圆柱的体积= 底面积 × 高
V
S
h
V=Sh
笑笑了解到一根柱子的底面半径0.4m,高为5m。你能算出它的体积吗?
从水杯里面量,水杯的底面直径是6cm,高是16cm,这个水杯能装多少毫升水?
3.14×0.42×5
=0.5024×5
=2.512(m3)
柱子的体积:
杯子的容积:
3.14×(6÷2)2×16
=28.26×16
=452.16(cm3)
452.16 cm3=452.16 mL
返回目录
随堂练习
教材第9页“练一练”第1题。
1.分别计算下列各图形的体积,再说说这几个
图形体积计算方法之间的联系。
4×3×8
=96(cm3)
6×6×6
=216(cm3)
3.14×(5÷2)2×8
=157(cm3)
教材第9页“练一练”第2题。
2.计算下面各圆柱的体积。
60×4=240(cm3)
3.14×12×5=15.7(cm3)
3.14×(6÷2)2×10=282.6(dm3)
返回目录
作业设计
作业1
作业2
我能行!
返回目录
作业1
教材第9页“练一练”第3题 。
3.这个杯子能否装下3000mL的牛奶?
3.14×(14÷2)2×20=3077.2(cm3)
3077.2 cm3=3077.2 mL
3077.2>3000
答:能装下3000 mL的牛奶。
返回作业设计
基础巩固
提升培优
思维创新
作业2
返回作业设计
基础巩固
1.(基础题)想一想,填一填。
(1)7.8米3=( )分米3
3升56毫升=( )毫升=( )立方厘米
7800
(2)一个圆柱形水杯(水杯厚度忽略不计),它的底面
积是10 cm2,高是12 cm,则这个水杯可以装水
( )升。
0.12
3056
3056
(3)一个圆柱的体积是62.8立方厘米,底面半径是
2厘米,则高是( )厘米。
5
基础巩固
2.(易错题)我是聪明的小法官。
(1)正方体、长方体和圆柱的体积都等于底面积
乘高。 ( )
√
(2)底面直径是4厘米的圆柱,其体积和侧面积一
样大。 ( )
×
(3)一个圆柱的高扩大到原来的2倍,底面半径缩小
到原来的 ,体积不变。 ( )
×
返回作业2
3.(重点题)把一块长31.4厘米,宽20厘米,高4
厘米的长方体钢坯锻造成底面积是50.24平方
厘米的圆柱形钢材,这根钢材长多少厘米?
提升培优
31.4×20×4÷50.24=50(厘米)
答:这根钢材长50厘米。
4.(难点题)两个底面积相等的圆柱体,其中一
个高为4.5 dm,体积为81 dm3;另一个高为3 dm,
求它的体积。
提升培优
81÷4.5×3=54(dm3)
答:它的体积是54 dm?。
返回作业2
5.(探究题)把一个棱长为6分米的正方体木块
削成一个最大的圆柱,这个圆柱的体积是多少
立方分米?
3.14×(6÷2)2×6=169.56(立方分米)
答:这个圆柱的体积是169.56立方分米。
思维创新
6.(创新题)一个圆柱,如果把它的高截短3厘
米,它的表面积减少94.2平方厘米,那么它的
体积减小多少立方厘米?
思维创新
返回作业2
3.14×(94.2÷3÷3.14÷2)2×3=235.5(立方厘米)
答:它的体积减少235.5立方厘米。
六年级数学·下 新课标[北师]
3 圆柱的体积
学习新知
随堂练习
作业设计
复习准备
第1课时 圆柱体积的计算方法
复 习 准 备
1.用字母表示下面的公式。
返回目录
S圆= ,V长方体= ,V正方体= 。?
πr2
abh
a?
2.求正方体和长方体的体积,可以用一个统一
的计算公式来表示,这个计算公式是什么?
V=Sh
学 习 新 知
长方体体积=长×宽×高
正方体体积=边长?
长(正)方体的体积=底面积×高
老朋友
新朋友
一个圆柱体所占空间的大小叫作圆柱的体积。
V=( )
V=( )
统一公式:V=( )
abh
a3
Sh
从叠硬币来看,用“底面积×高”能计算出圆柱的体积。
问题
a.你准备把圆柱体转化成什么立体图形?
b.你是怎样转化成这个立体图形的?
c.转化以后的立体图形和圆柱体之间有什么
关系?
底面积相等
圆柱的高于长方体的高相等
圆柱的体积= 底面积 × 高
V
S
h
V=Sh
笑笑了解到一根柱子的底面半径0.4m,高为5m。你能算出它的体积吗?
从水杯里面量,水杯的底面直径是6cm,高是16cm,这个水杯能装多少毫升水?
3.14×0.42×5
=0.5024×5
=2.512(m3)
柱子的体积:
杯子的容积:
3.14×(6÷2)2×16
=28.26×16
=452.16(cm3)
452.16 cm3=452.16 mL
返回目录
随堂练习
教材第9页“练一练”第1题。
1.分别计算下列各图形的体积,再说说这几个
图形体积计算方法之间的联系。
4×3×8
=96(cm3)
6×6×6
=216(cm3)
3.14×(5÷2)2×8
=157(cm3)
教材第9页“练一练”第2题。
2.计算下面各圆柱的体积。
60×4=240(cm3)
3.14×12×5=15.7(cm3)
3.14×(6÷2)2×10=282.6(dm3)
返回目录
作业设计
作业1
作业2
我能行!
返回目录
作业1
教材第9页“练一练”第3题 。
3.这个杯子能否装下3000mL的牛奶?
3.14×(14÷2)2×20=3077.2(cm3)
3077.2 cm3=3077.2 mL
3077.2>3000
答:能装下3000 mL的牛奶。
返回作业设计
基础巩固
提升培优
思维创新
作业2
返回作业设计
基础巩固
1.(基础题)想一想,填一填。
(1)7.8米3=( )分米3
3升56毫升=( )毫升=( )立方厘米
7800
(2)一个圆柱形水杯(水杯厚度忽略不计),它的底面
积是10 cm2,高是12 cm,则这个水杯可以装水
( )升。
0.12
3056
3056
(3)一个圆柱的体积是62.8立方厘米,底面半径是
2厘米,则高是( )厘米。
5
基础巩固
2.(易错题)我是聪明的小法官。
(1)正方体、长方体和圆柱的体积都等于底面积
乘高。 ( )
√
(2)底面直径是4厘米的圆柱,其体积和侧面积一
样大。 ( )
×
(3)一个圆柱的高扩大到原来的2倍,底面半径缩小
到原来的 ,体积不变。 ( )
×
返回作业2
3.(重点题)把一块长31.4厘米,宽20厘米,高4
厘米的长方体钢坯锻造成底面积是50.24平方
厘米的圆柱形钢材,这根钢材长多少厘米?
提升培优
31.4×20×4÷50.24=50(厘米)
答:这根钢材长50厘米。
4.(难点题)两个底面积相等的圆柱体,其中一
个高为4.5 dm,体积为81 dm3;另一个高为3 dm,
求它的体积。
提升培优
81÷4.5×3=54(dm3)
答:它的体积是54 dm?。
返回作业2
5.(探究题)把一个棱长为6分米的正方体木块
削成一个最大的圆柱,这个圆柱的体积是多少
立方分米?
3.14×(6÷2)2×6=169.56(立方分米)
答:这个圆柱的体积是169.56立方分米。
思维创新
6.(创新题)一个圆柱,如果把它的高截短3厘
米,它的表面积减少94.2平方厘米,那么它的
体积减小多少立方厘米?
思维创新
返回作业2
3.14×(94.2÷3÷3.14÷2)2×3=235.5(立方厘米)
答:它的体积减少235.5立方厘米。
