2020-2021学年人教版八年级下册数学第18章平行四边形(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学第18章平行四边形(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 248.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-23 00:00:00 | ||
图片预览



文档简介
第18章
《平行四边形》单元测试
一.选择题(每题3分,共30分)
1.平行四边形和矩形都具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.每条对角线平分一组对角
2.如图,菱形ABCD的周长为16,若∠BAD=60°,E是AB的中点,则点E的坐标为(
)
A.(1,1)
B.
C.
D.
3.如图,在菱形中,对角线AC、BD的长分别为8cm、6cm,则这个菱形的周长为(
)
A.10cm
B.14cm
C.20cm
D.28cm
4.不能判定四边形ABCD为平行四边形的题设是( )
A.AB=CD,AB∥CD
B.∠A=∠C,∠B=∠D
C.AB=AD,BC=CD
D.AB=CD,AD=BC
5.如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为(
)
A.
B.4
C.5
D.
6.如图,在△ABC中,点D,E,F分别是BC,AB,
AC的中点,则下列四个判断中不一定正确的是(
)
A.四边形AEDF一定是平行四边形
B.若∠A=90°,则四边形AEDF是矩形
C.若AD平分∠A,则四边形AEDF是正方形
D.若AD⊥BC,则四边形AEDF是菱形
7.如图所示,直线a∥b,A是直线a上的一个定点,线段BC在直线b上移动,那么在移动过程中△ABC的面积(
)
A.变大
B.变小
C.不变
D.无法确定
8.
(2020·深圳)如图,矩形纸片ABCD中,AB=6,BC=12.将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:
①EF⊥BG;②GE=GF;③△GDK和△GKH的面积相等;④当点F与点C重合时,∠DEF=75°.其中正确的结论共有( )
A.1个
B.2个
C.3个
D.4个
9.如图,中,分别是的中点,点在上,且,当时,的长是(
?
???)
A.9
B.10.5
C.12
D.18
10.下列说法中错误的是(
)
A.四个角相等的四边形是矩形
B.四条边相等的四边形是正方形
C.对角线相等的菱形是正方形
D.对角线垂直的矩形是正方形
二.填空题(每题4分,共20分)
11.
如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE.如果∠ADB=30°,则∠E=________度.
12.
(2020·四川甘孜州)如图,有一张长方形纸片ABCD,AB=8cm,BC=10cm,点E为CD上一点,将纸片沿AE折叠,BC的对应边B'C'恰好经过点D,则线段DE的长为__________cm.
13.四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE=,则CE的长为______.
14.如图,正方形ABCD的边长为1,点P为边BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为__,最小值为__.
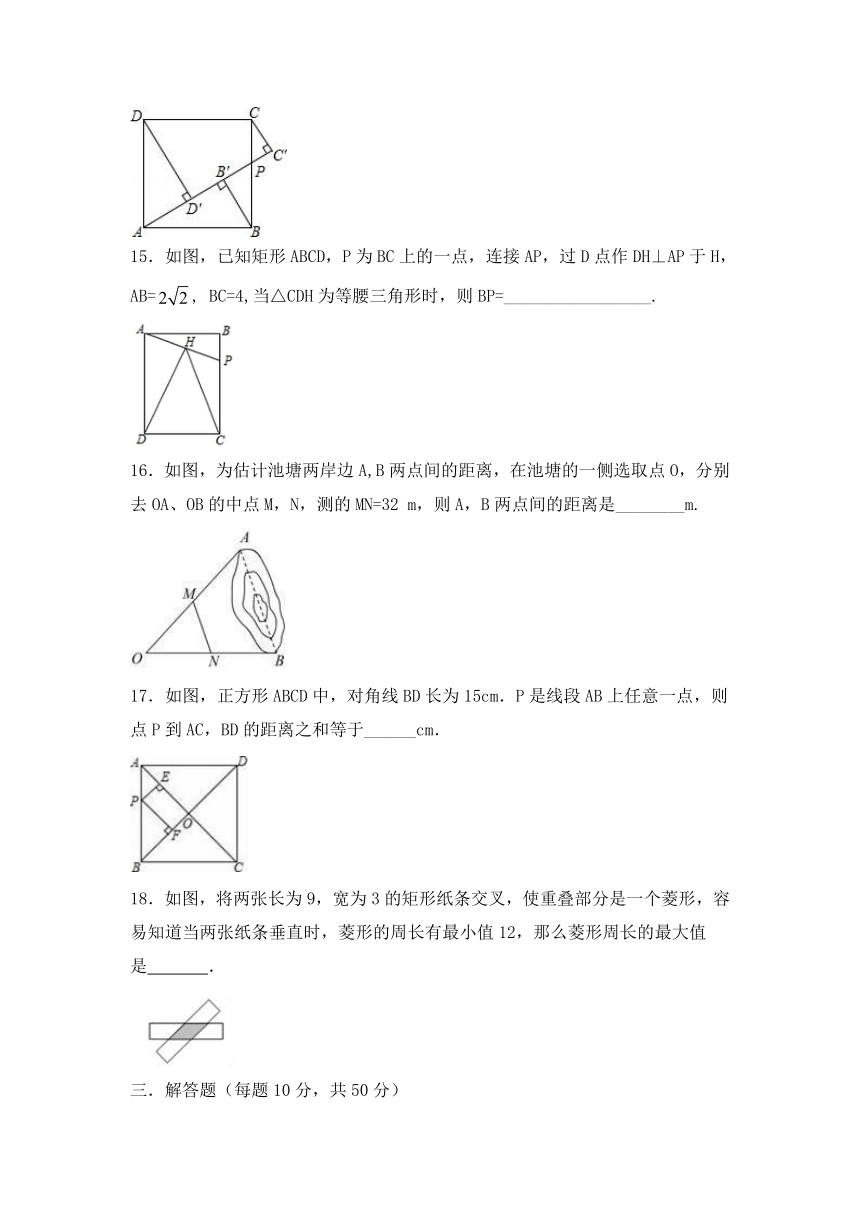
15.如图,已知矩形ABCD,P为BC上的一点,连接AP,过D点作DH⊥AP于H,AB=,
BC=4,当△CDH为等腰三角形时,则BP=_________________.
16.如图,为估计池塘两岸边A,B两点间的距离,在池塘的一侧选取点O,分别去OA、OB的中点M,N,测的MN=32
m,则A,B两点间的距离是________m.
17.如图,正方形ABCD中,对角线BD长为15cm.P是线段AB上任意一点,则点P到AC,BD的距离之和等于______cm.
18.如图,将两张长为9,宽为3的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值12,那么菱形周长的最大值是
.
三.解答题(每题10分,共50分)
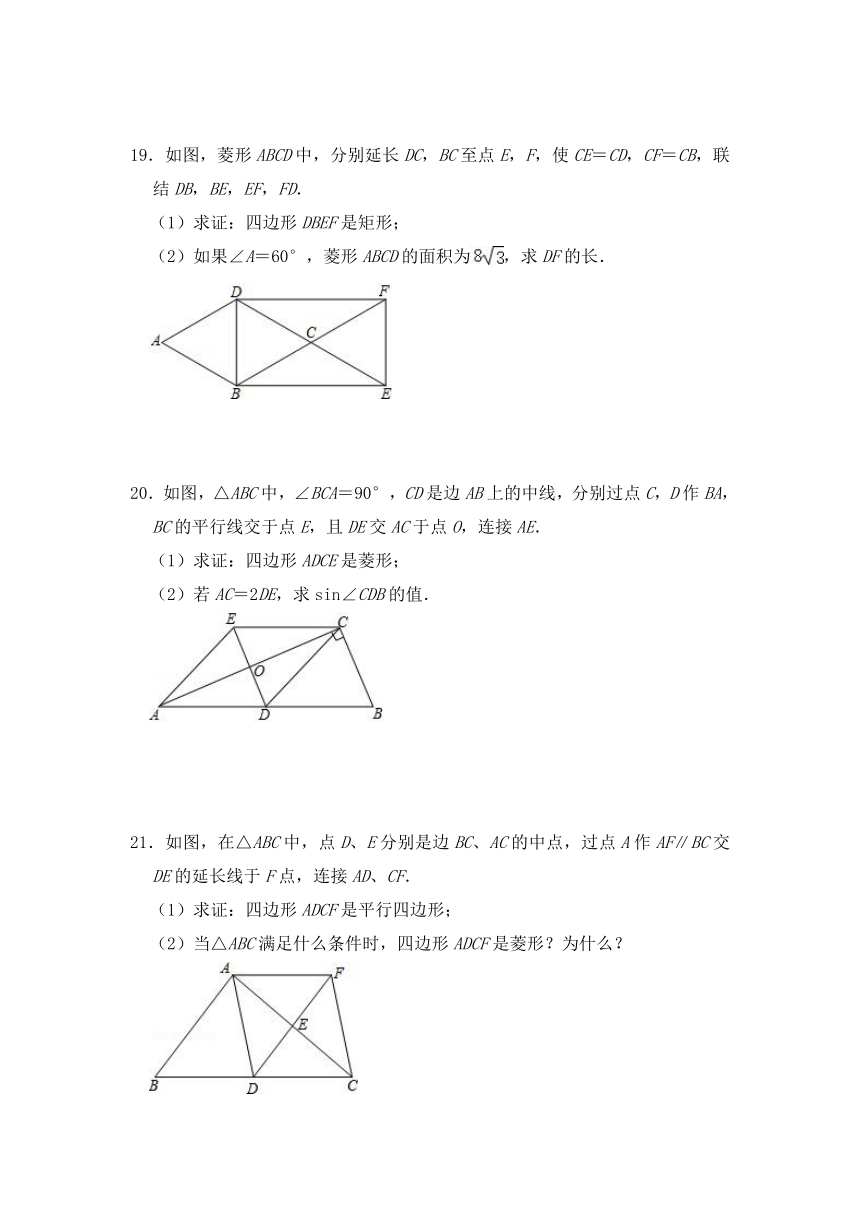
19.如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.
(1)求证:四边形DBEF是矩形;
(2)如果∠A=60°,菱形ABCD的面积为,求DF的长.
20.如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
21.如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是菱形?为什么?
22.如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?
23.如图,E是?ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
参考答案
一.选择题
1.A
2.B
3.C
4.
C.
5.D
6.C.
7.C.
8.C
9.
C.10.B
二.填空题(共5小题)
11.15
12.5
13.或
14.2
15.、或2
16.64.
17.7.5.
18.20.
三.解答题(共5小题)
19.(1)证明:∵CE=CD,CF=CB,
∴四边形DBEF是平行四边形.
∵四边形ABCD是菱形,
∴CD=CB.
∴CE=CF,
∴BF=DE,
∴四边形DBEF是矩形.
(2)设DB为2a,
∵∠A=60°,菱形ABCD的面积为,
∴可得,
解得:a=2,
∴DB=4,
∵∠DBC=60°,
∴DF=.
20.(1)证明:∵DE∥BC,CE∥AB,
∴四边形DBCE是平行四边形.
∴CE=BD,
又∵CD是边AB上的中线,
∴BD=AD,
∴CE=DA,
又∵CE∥DA,
∴四边形ADCE是平行四边形.
∵∠BCA=90°,CD是斜边AB上的中线,
∴AD=CD,
∴四边形ADCE是菱形;
(2)解:过点C作CF⊥AB于点F,
由(1)可知,BC=DE,
设BC=x,则AC=2x,
在Rt△ABC中,AB==x.
∵AB?CF=AC?BC,
∴CF==x.
∵CD=AB=x,
∴sin∠CDB==.
21.(1)证明:∵点D、E分别是边BC、AC的中点,
∴DE∥AB,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∴AF=BD,则AF=DC,
∵AF∥BC,
∴四边形ADCF是平行四边形;
(2)当△ABC是直角三角形时,四边形ADCF是菱形,
理由:∵点D是边BC的中点,△ABC是直角三角形,
∴AD=DC,
∴平行四边形ADCF是菱形.
22.解:(1)由作图知:PQ为线段AC的垂直平分线,
∴AE=CE,AD=CD,
∵CF∥AB,
∴∠EAC=∠FCA,∠CFD=∠AED,
在△AED与△CFD中,
,
∴△AED≌△CFD;
(2)∵△AED≌△CFD,
∴AE=CF,
∵EF为线段AC的垂直平分线,
∴EC=EA,FC=FA,
∴EC=EA=FC=FA,
∴四边形AECF为菱形.
(3)∵AD=3,AE=5,
∴根据勾股定理得:ED=4,
∴EF=8,AC=6,
∴S菱形AECF=8×6÷2=24,
∴菱形AECF的面积是24
23.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAE=∠F,∠D=∠ECF,
∵E是?ABCD的边CD的中点,
∴DE=CE,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS);
(2)解:∵△ADE≌△FCE,
∴AE=EF=3,
∵AB∥CD,
∴∠AED=∠BAF=90°,
在?ABCD中,AD=BC=5,
∴DE===4,
∴CD=2DE=8.
《平行四边形》单元测试
一.选择题(每题3分,共30分)
1.平行四边形和矩形都具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.每条对角线平分一组对角
2.如图,菱形ABCD的周长为16,若∠BAD=60°,E是AB的中点,则点E的坐标为(
)
A.(1,1)
B.
C.
D.
3.如图,在菱形中,对角线AC、BD的长分别为8cm、6cm,则这个菱形的周长为(
)
A.10cm
B.14cm
C.20cm
D.28cm
4.不能判定四边形ABCD为平行四边形的题设是( )
A.AB=CD,AB∥CD
B.∠A=∠C,∠B=∠D
C.AB=AD,BC=CD
D.AB=CD,AD=BC
5.如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为(
)
A.
B.4
C.5
D.
6.如图,在△ABC中,点D,E,F分别是BC,AB,
AC的中点,则下列四个判断中不一定正确的是(
)
A.四边形AEDF一定是平行四边形
B.若∠A=90°,则四边形AEDF是矩形
C.若AD平分∠A,则四边形AEDF是正方形
D.若AD⊥BC,则四边形AEDF是菱形
7.如图所示,直线a∥b,A是直线a上的一个定点,线段BC在直线b上移动,那么在移动过程中△ABC的面积(
)
A.变大
B.变小
C.不变
D.无法确定
8.
(2020·深圳)如图,矩形纸片ABCD中,AB=6,BC=12.将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:
①EF⊥BG;②GE=GF;③△GDK和△GKH的面积相等;④当点F与点C重合时,∠DEF=75°.其中正确的结论共有( )
A.1个
B.2个
C.3个
D.4个
9.如图,中,分别是的中点,点在上,且,当时,的长是(
?
???)
A.9
B.10.5
C.12
D.18
10.下列说法中错误的是(
)
A.四个角相等的四边形是矩形
B.四条边相等的四边形是正方形
C.对角线相等的菱形是正方形
D.对角线垂直的矩形是正方形
二.填空题(每题4分,共20分)
11.
如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE.如果∠ADB=30°,则∠E=________度.
12.
(2020·四川甘孜州)如图,有一张长方形纸片ABCD,AB=8cm,BC=10cm,点E为CD上一点,将纸片沿AE折叠,BC的对应边B'C'恰好经过点D,则线段DE的长为__________cm.
13.四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE=,则CE的长为______.
14.如图,正方形ABCD的边长为1,点P为边BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为__,最小值为__.
15.如图,已知矩形ABCD,P为BC上的一点,连接AP,过D点作DH⊥AP于H,AB=,
BC=4,当△CDH为等腰三角形时,则BP=_________________.
16.如图,为估计池塘两岸边A,B两点间的距离,在池塘的一侧选取点O,分别去OA、OB的中点M,N,测的MN=32
m,则A,B两点间的距离是________m.
17.如图,正方形ABCD中,对角线BD长为15cm.P是线段AB上任意一点,则点P到AC,BD的距离之和等于______cm.
18.如图,将两张长为9,宽为3的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值12,那么菱形周长的最大值是
.
三.解答题(每题10分,共50分)
19.如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.
(1)求证:四边形DBEF是矩形;
(2)如果∠A=60°,菱形ABCD的面积为,求DF的长.
20.如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
21.如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是菱形?为什么?
22.如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?
23.如图,E是?ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
参考答案
一.选择题
1.A
2.B
3.C
4.
C.
5.D
6.C.
7.C.
8.C
9.
C.10.B
二.填空题(共5小题)
11.15
12.5
13.或
14.2
15.、或2
16.64.
17.7.5.
18.20.
三.解答题(共5小题)
19.(1)证明:∵CE=CD,CF=CB,
∴四边形DBEF是平行四边形.
∵四边形ABCD是菱形,
∴CD=CB.
∴CE=CF,
∴BF=DE,
∴四边形DBEF是矩形.
(2)设DB为2a,
∵∠A=60°,菱形ABCD的面积为,
∴可得,
解得:a=2,
∴DB=4,
∵∠DBC=60°,
∴DF=.
20.(1)证明:∵DE∥BC,CE∥AB,
∴四边形DBCE是平行四边形.
∴CE=BD,
又∵CD是边AB上的中线,
∴BD=AD,
∴CE=DA,
又∵CE∥DA,
∴四边形ADCE是平行四边形.
∵∠BCA=90°,CD是斜边AB上的中线,
∴AD=CD,
∴四边形ADCE是菱形;
(2)解:过点C作CF⊥AB于点F,
由(1)可知,BC=DE,
设BC=x,则AC=2x,
在Rt△ABC中,AB==x.
∵AB?CF=AC?BC,
∴CF==x.
∵CD=AB=x,
∴sin∠CDB==.
21.(1)证明:∵点D、E分别是边BC、AC的中点,
∴DE∥AB,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∴AF=BD,则AF=DC,
∵AF∥BC,
∴四边形ADCF是平行四边形;
(2)当△ABC是直角三角形时,四边形ADCF是菱形,
理由:∵点D是边BC的中点,△ABC是直角三角形,
∴AD=DC,
∴平行四边形ADCF是菱形.
22.解:(1)由作图知:PQ为线段AC的垂直平分线,
∴AE=CE,AD=CD,
∵CF∥AB,
∴∠EAC=∠FCA,∠CFD=∠AED,
在△AED与△CFD中,
,
∴△AED≌△CFD;
(2)∵△AED≌△CFD,
∴AE=CF,
∵EF为线段AC的垂直平分线,
∴EC=EA,FC=FA,
∴EC=EA=FC=FA,
∴四边形AECF为菱形.
(3)∵AD=3,AE=5,
∴根据勾股定理得:ED=4,
∴EF=8,AC=6,
∴S菱形AECF=8×6÷2=24,
∴菱形AECF的面积是24
23.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAE=∠F,∠D=∠ECF,
∵E是?ABCD的边CD的中点,
∴DE=CE,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS);
(2)解:∵△ADE≌△FCE,
∴AE=EF=3,
∵AB∥CD,
∴∠AED=∠BAF=90°,
在?ABCD中,AD=BC=5,
∴DE===4,
∴CD=2DE=8.
