27.4正多边形和圆 同步课时训练(含答案)
文档属性
| 名称 | 27.4正多边形和圆 同步课时训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 481.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-21 16:14:34 | ||
图片预览



文档简介
27.4正多边形和圆课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.正六边形的边心距为false,这个正六边形的面积为( )
A.12 B.false C.false D.false
2.已知⊙O的半径是2,一个正方形内接于⊙O,则这个正方形的边长是( )
A.2false B.2 C.false D.4
3.如图,△ABC中,内切圆I和边BC,AC,AB分别相切于点D,E,F,若false,则∠EDF的度数是( )
A.false B.false C.false D.false
4.如图,正五边形false内接于false,点false为false上一点(点false与点false,点false不重合),连接false,false,false,垂足为false,则false等于( )
A.72° B.54° C.36° D.64°
5.如图,螺母的外围可以看作是正六边形ABCDEF,己知这个正六边形的半径是2,则它的周长是( )
A.6false B.12false C.12 D.24
6.如图,在false中,false,false,false,⊙O是false的内切圆,则⊙O的半径为( )
A.1 B.false C.2 D.false
7.如图,点false和false分别是false的内心和外心,若false,则false( )
A.false B.false C.false D.false
8.已知四边形ABCD,下列命题:①若false,则四边形ABCD一定存在外接圆;②若四边形ABCD内存在一点到四个顶点的距离相等,则false;③若四边形ABCD内存在一点到四条边的距离相等,则false,其中,真命题的个数为( )
A.0 B.1 C.2 D.3
9.如图,点I为false的内心,false,false,false,将false平移使其顶点与I重合,则图中阴影部分的周长为( )
A.6 B.4 C.3 D.6.5
10.⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )
A.1∶false B.false∶false C.3∶2 D.1∶2
二、填空题
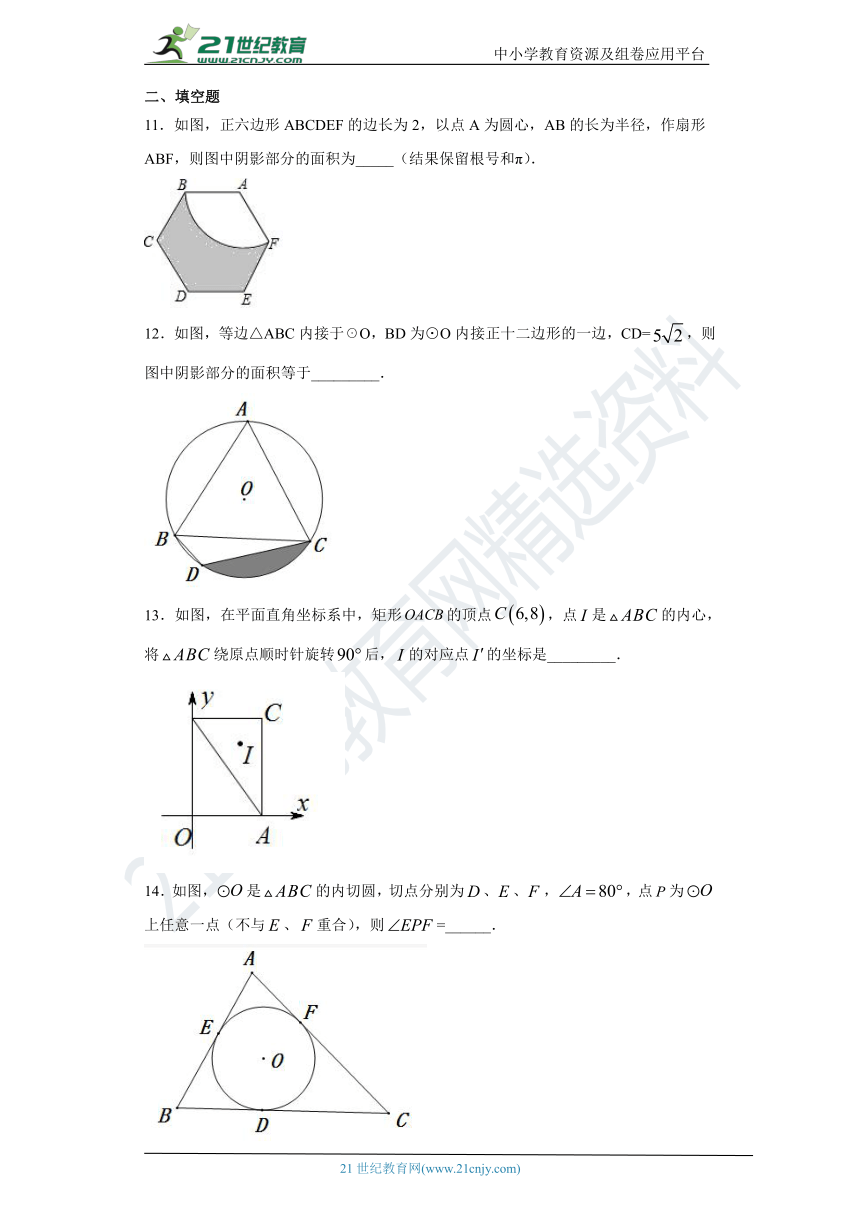
11.如图,正六边形ABCDEF的边长为2,以点A为圆心,AB的长为半径,作扇形ABF,则图中阴影部分的面积为_____(结果保留根号和π).
12.如图,等边△ABC内接于☉O,BD为⊙O内接正十二边形的一边,CD=false,则图中阴影部分的面积等于_________.
13.如图,在平面直角坐标系中,矩形false的顶点false,点false是false的内心,将false绕原点顺时针旋转false后,false的对应点false的坐标是_________.
14.如图,false是false的内切圆,切点分别为false、false、false,false,点false为false上任意一点(不与false、false重合),则false=______.
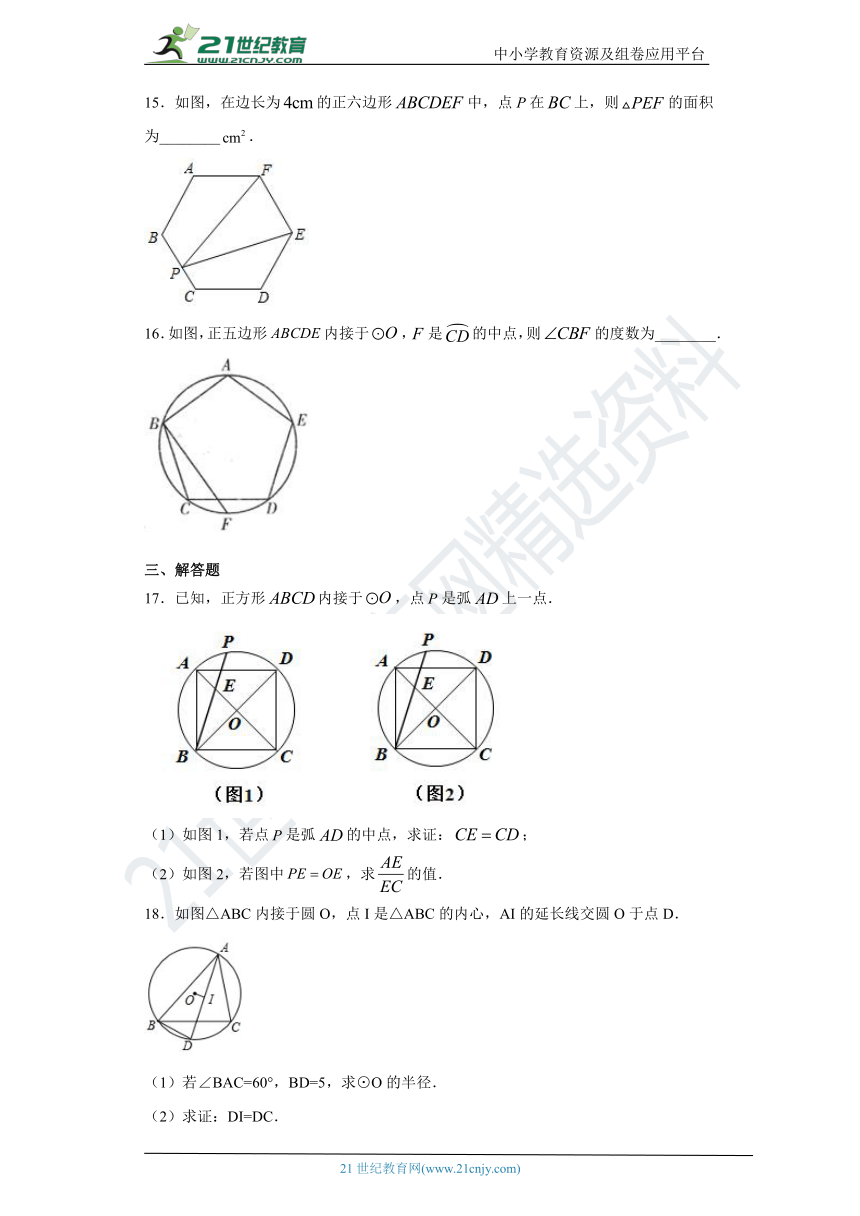
15.如图,在边长为false的正六边形false中,点P在false上,则false的面积为________false.
16.如图,正五边形false内接于false,false是false的中点,则false的度数为________.
三、解答题
17.已知,正方形false内接于false,点false是弧false上一点.
(1)如图1,若点false是弧false的中点,求证:false;
(2)如图2,若图中false,求false的值.
18.如图△ABC内接于圆O,点I是△ABC的内心,AI的延长线交圆O于点D.
false
(1)若∠BAC=60°,BD=5,求⊙O的半径.
(2)求证:DI=DC.
19.如图,已知,在以AB为弦的弓形劣弧上取一点M(不包括A,B两点),以M为圆心作圆M和AB相切,分别过A,B作⊙M的切线,两条切线相交于点C.求证:∠ACB为定值.
20.如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与false轴交于A、B两点(点A在点B的左侧),与false轴交于点C.抛物线的对称轴与false轴交于点E,点P在对称轴上.
(1)求抛物线的解析式;
(2)直线CM与false轴交于点D,若false,求点P的坐标;
(3)请探索:是否存在这样的点P,使false?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
1.B
2.A
3.D
4.B
5.C
6.A
7.D
8.D
9.A
10.B
11.6false﹣falseπ
12.false
13.false
14.50°或130°
15.false
16.false
17.(1)见解析;(2)false
【详解】
解:(1)∵四边形ABCD是正方形,
false.
∵false是弧false的中点,
∴false,
false,
false,
false,
false,
false.
(2)如图,连接DP,DE,
∵正方形false内接于false,
∴BD是false的直径,
∴false.
∵AC,BD是正方形ABCD的对角线,
∴AC垂直平分BD,false,
false,
false.
∵false,
∴点E在false的平分线上,
false,
false.
在false中,false,
false,
∴false,
false,
∴false.
18.(1)5;(2)见解析
【详解】
(1)解:连结OB,OD,
∵点I是△ABC的内心,∠BAC=60°
∴∠BAD=∠CAD=30°
∴∠BOD=60°
∵OB=OD
∴△BOD是等边三角形
∴OB=BD=5
(2)证明:连结BI,CD,
∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠ABI=∠CBI,∠BAD=∠CAD=∠CBD,
∵∠BID=∠ABI+∠BAD,
又∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴ID=BD,
∵∠BAD=∠CAD
∴CD=BD,
∴DB=DC=DI;
∴DI=DC.
19.见解析.
【详解】
证明:连接AM,BM,
由题意得:M是内心,
∴AM平分∠CAB,BM平分∠ABC,
∴∠CAM=∠BAM,∠CBM=∠ABM,
∴∠AMB=180°﹣∠BAM﹣∠ABM,
∴∠BAM+∠ABM=180°﹣∠AMB,
△ABC中,∠C=180°﹣(∠CAB+∠ACB)=180°﹣2∠BAM﹣2∠ABM=180°﹣2(180°﹣∠AMB)=2∠AMB﹣180°,
∵false所在圆是个定圆,弦AB和半径都是定值,
∴∠AMB为定值,
∴∠ACB为定值2∠AMB﹣180°.
20.(1)y=-x2+2x+3;(2)P(1,2)或(1,-2);(3)P(1,false+1)或(1,-false-1).
【详解】
解:(1)设抛物线为y=a(x-1)2+4.
∵抛物线过点(2,3)
∴3=a(2-1)2+4,解得a=-1
∴抛物线的解析式为y=-(x-1)2+4,即y=-x2+2x+3;
(2)如图1,令y=0,则-(x-1)2+4=0,解得x=-1或x=3,
∴A(-1,0),B(3,0),
令x=0,可得y=3
∴C(0,3),
∵M(1,4)
∴运用待定系数法可得:直线CM的解析式为y=x+3
令y=0,则x+3=0,x=-3,
∴D(-3,0)
∵∠DEM=∠AEP=90°,∠DMB=∠APE.
∴△DEM∽△AEP,
∴false
∵A(-1,0),E(1,0),D(-3,0),M(1,4).
∴DE=4,ME=4,AE=2.
∴false,即PE=2
∴P(1,2)或(1,-2);
(3)存在,P的坐标为(1,false+1)或(1,-false-1),理由如下:
如图2,①当点P在x轴上方时,连接BP,
∵PE是抛物线的对称轴,
∴∠APE=∠BPE,∠APB=2∠APE
∵∠ANB=2∠APE
∴∠ANB=∠APB
∴点A,B,N,P四点共圆,
设圆心F的坐标为(1,n),即PF=AF=NF,
∵A(-1,0),N(2,3)
∴false
∴n2+4=1+(3-n)2,解得n=1
∴F(1,1),即PF=AF=false
∴PE=false+1,P(1,false+1);
②当点P在x轴下方时,由对称知,P(1,-false-1);
综上,点P的坐标为P(1,false+1)或(1,-false-1).
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.正六边形的边心距为false,这个正六边形的面积为( )
A.12 B.false C.false D.false
2.已知⊙O的半径是2,一个正方形内接于⊙O,则这个正方形的边长是( )
A.2false B.2 C.false D.4
3.如图,△ABC中,内切圆I和边BC,AC,AB分别相切于点D,E,F,若false,则∠EDF的度数是( )
A.false B.false C.false D.false
4.如图,正五边形false内接于false,点false为false上一点(点false与点false,点false不重合),连接false,false,false,垂足为false,则false等于( )
A.72° B.54° C.36° D.64°
5.如图,螺母的外围可以看作是正六边形ABCDEF,己知这个正六边形的半径是2,则它的周长是( )
A.6false B.12false C.12 D.24
6.如图,在false中,false,false,false,⊙O是false的内切圆,则⊙O的半径为( )
A.1 B.false C.2 D.false
7.如图,点false和false分别是false的内心和外心,若false,则false( )
A.false B.false C.false D.false
8.已知四边形ABCD,下列命题:①若false,则四边形ABCD一定存在外接圆;②若四边形ABCD内存在一点到四个顶点的距离相等,则false;③若四边形ABCD内存在一点到四条边的距离相等,则false,其中,真命题的个数为( )
A.0 B.1 C.2 D.3
9.如图,点I为false的内心,false,false,false,将false平移使其顶点与I重合,则图中阴影部分的周长为( )
A.6 B.4 C.3 D.6.5
10.⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )
A.1∶false B.false∶false C.3∶2 D.1∶2
二、填空题
11.如图,正六边形ABCDEF的边长为2,以点A为圆心,AB的长为半径,作扇形ABF,则图中阴影部分的面积为_____(结果保留根号和π).
12.如图,等边△ABC内接于☉O,BD为⊙O内接正十二边形的一边,CD=false,则图中阴影部分的面积等于_________.
13.如图,在平面直角坐标系中,矩形false的顶点false,点false是false的内心,将false绕原点顺时针旋转false后,false的对应点false的坐标是_________.
14.如图,false是false的内切圆,切点分别为false、false、false,false,点false为false上任意一点(不与false、false重合),则false=______.
15.如图,在边长为false的正六边形false中,点P在false上,则false的面积为________false.
16.如图,正五边形false内接于false,false是false的中点,则false的度数为________.
三、解答题
17.已知,正方形false内接于false,点false是弧false上一点.
(1)如图1,若点false是弧false的中点,求证:false;
(2)如图2,若图中false,求false的值.
18.如图△ABC内接于圆O,点I是△ABC的内心,AI的延长线交圆O于点D.
false
(1)若∠BAC=60°,BD=5,求⊙O的半径.
(2)求证:DI=DC.
19.如图,已知,在以AB为弦的弓形劣弧上取一点M(不包括A,B两点),以M为圆心作圆M和AB相切,分别过A,B作⊙M的切线,两条切线相交于点C.求证:∠ACB为定值.
20.如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与false轴交于A、B两点(点A在点B的左侧),与false轴交于点C.抛物线的对称轴与false轴交于点E,点P在对称轴上.
(1)求抛物线的解析式;
(2)直线CM与false轴交于点D,若false,求点P的坐标;
(3)请探索:是否存在这样的点P,使false?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
1.B
2.A
3.D
4.B
5.C
6.A
7.D
8.D
9.A
10.B
11.6false﹣falseπ
12.false
13.false
14.50°或130°
15.false
16.false
17.(1)见解析;(2)false
【详解】
解:(1)∵四边形ABCD是正方形,
false.
∵false是弧false的中点,
∴false,
false,
false,
false,
false,
false.
(2)如图,连接DP,DE,
∵正方形false内接于false,
∴BD是false的直径,
∴false.
∵AC,BD是正方形ABCD的对角线,
∴AC垂直平分BD,false,
false,
false.
∵false,
∴点E在false的平分线上,
false,
false.
在false中,false,
false,
∴false,
false,
∴false.
18.(1)5;(2)见解析
【详解】
(1)解:连结OB,OD,
∵点I是△ABC的内心,∠BAC=60°
∴∠BAD=∠CAD=30°
∴∠BOD=60°
∵OB=OD
∴△BOD是等边三角形
∴OB=BD=5
(2)证明:连结BI,CD,
∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠ABI=∠CBI,∠BAD=∠CAD=∠CBD,
∵∠BID=∠ABI+∠BAD,
又∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴ID=BD,
∵∠BAD=∠CAD
∴CD=BD,
∴DB=DC=DI;
∴DI=DC.
19.见解析.
【详解】
证明:连接AM,BM,
由题意得:M是内心,
∴AM平分∠CAB,BM平分∠ABC,
∴∠CAM=∠BAM,∠CBM=∠ABM,
∴∠AMB=180°﹣∠BAM﹣∠ABM,
∴∠BAM+∠ABM=180°﹣∠AMB,
△ABC中,∠C=180°﹣(∠CAB+∠ACB)=180°﹣2∠BAM﹣2∠ABM=180°﹣2(180°﹣∠AMB)=2∠AMB﹣180°,
∵false所在圆是个定圆,弦AB和半径都是定值,
∴∠AMB为定值,
∴∠ACB为定值2∠AMB﹣180°.
20.(1)y=-x2+2x+3;(2)P(1,2)或(1,-2);(3)P(1,false+1)或(1,-false-1).
【详解】
解:(1)设抛物线为y=a(x-1)2+4.
∵抛物线过点(2,3)
∴3=a(2-1)2+4,解得a=-1
∴抛物线的解析式为y=-(x-1)2+4,即y=-x2+2x+3;
(2)如图1,令y=0,则-(x-1)2+4=0,解得x=-1或x=3,
∴A(-1,0),B(3,0),
令x=0,可得y=3
∴C(0,3),
∵M(1,4)
∴运用待定系数法可得:直线CM的解析式为y=x+3
令y=0,则x+3=0,x=-3,
∴D(-3,0)
∵∠DEM=∠AEP=90°,∠DMB=∠APE.
∴△DEM∽△AEP,
∴false
∵A(-1,0),E(1,0),D(-3,0),M(1,4).
∴DE=4,ME=4,AE=2.
∴false,即PE=2
∴P(1,2)或(1,-2);
(3)存在,P的坐标为(1,false+1)或(1,-false-1),理由如下:
如图2,①当点P在x轴上方时,连接BP,
∵PE是抛物线的对称轴,
∴∠APE=∠BPE,∠APB=2∠APE
∵∠ANB=2∠APE
∴∠ANB=∠APB
∴点A,B,N,P四点共圆,
设圆心F的坐标为(1,n),即PF=AF=NF,
∵A(-1,0),N(2,3)
∴false
∴n2+4=1+(3-n)2,解得n=1
∴F(1,1),即PF=AF=false
∴PE=false+1,P(1,false+1);
②当点P在x轴下方时,由对称知,P(1,-false-1);
综上,点P的坐标为P(1,false+1)或(1,-false-1).
