第三章 全等三角形
图片预览




文档简介
岳纸学校教学学案44
年级: 班级: 姓名:
课 题 3.1旋转 课型 新授课
学习知识点 性质1 对应点到旋转中心的距离相等性质2 对应点与旋转中心的连线所成的角彼此相等,且等于旋转角性质3 旋转不改变图形的形状和大小
学习重点 旋转图形的性质
学习难点 旋转图形的画法
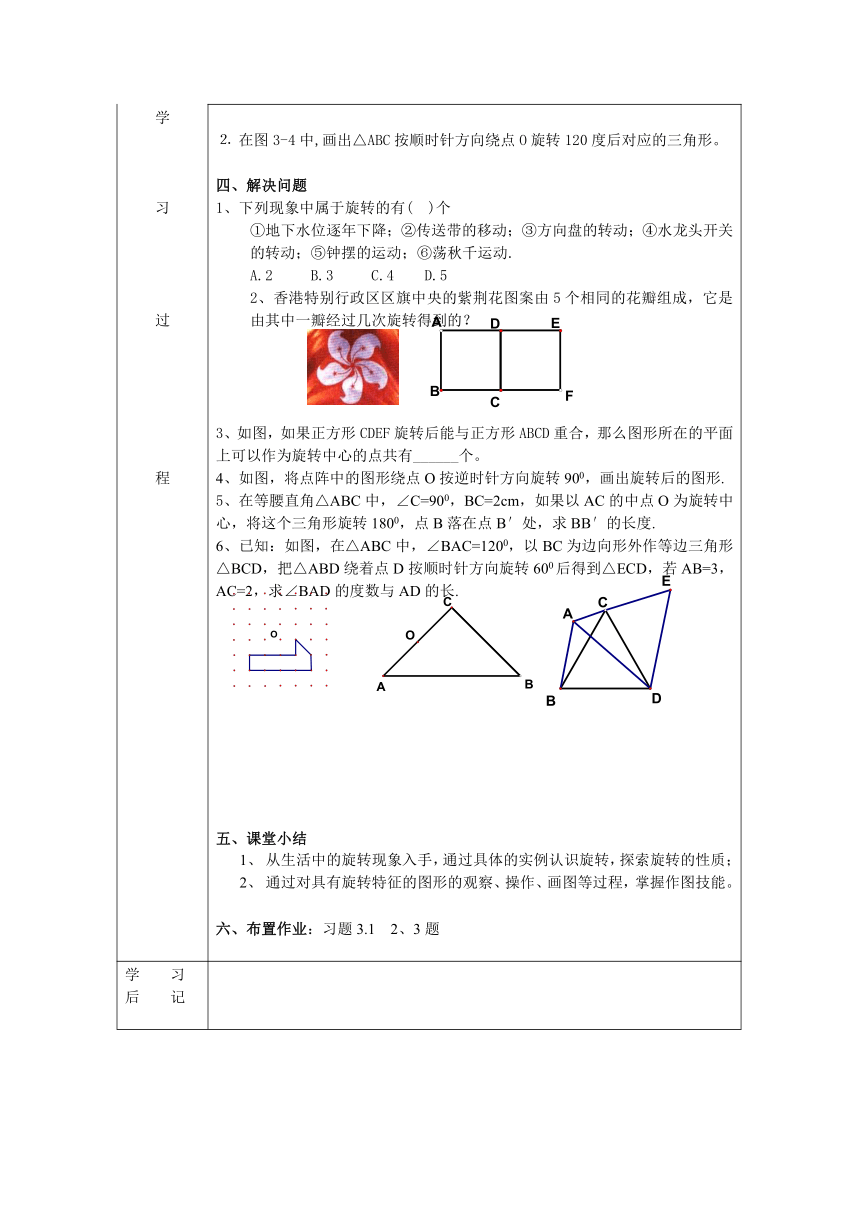
学 习 过 程学 习 过 程 一、课前预习与导学 (1)在平面内,将一个图形绕一个__ _旋转_ _角度,这样的图形运动称为图形的旋转。这个定点为_____。图形绕旋转中心沿着某个方向转过的角成______.(2)旋转前后的图形_____(对应线段__,对应角_____)。(3)对应点到旋转中心的距离________。(4)每一对对应点与旋转中心的连线所成的角彼此_。(5)如图,画出⊿ABC绕点A逆时针旋转90°后的图形。二、新课1、手工制作:制作一个小风车. 2、欣赏日常生活中部分物体的旋转现象. 提出问题:⑴上述情境中的旋转现象有什么共同的特征? ⑵生活还有类似的例子吗? 3、图形的旋转在平面内,将一个图形绕一个 旋转一定的 ,这样的图形运动叫做 。这个定点叫 。旋转的角度称为 。操作活动(1)将一块三角尺ABC绕点C按逆时针方向旋转到DCB的位置 问题: 度量∠ACD与∠BCE的度数,线段AC与DC、BC与EC的长度。你发现了什么?(2)将△ABC绕点O按顺时针方向旋转到△A/ B/C/的位置。 问题:度量∠AO A/、∠BO B/、∠CO C/的度数,线段AO与A/O、BO与B/O、CO与C/O的长度。你发现了什么?三、练一练:⒈ 已知线段AB和点O,按下面的方法画出线段AB绕点O按逆时针方向旋转100°后的图形:⒉ 在图3-4中,画出△ABC按顺时针方向绕点O旋转120度后对应的三角形。四、解决问题1、下列现象中属于旋转的有( )个①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.A.2 B.3 C.4 D.5 2、香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?3、如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个。 4、如图,将点阵中的图形绕点O按逆时针方向旋转900,画出旋转后的图形.5、在等腰直角△ABC中,∠C=900,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转1800,点B落在点B′处,求BB′的长度. 6、已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.五、课堂小结从生活中的旋转现象入手,通过具体的实例认识旋转,探索旋转的性质;通过对具有旋转特征的图形的观察、操作、画图等过程,掌握作图技能。六、布置作业:习题3.1 2、3题
学 习后 记
岳纸学校教学学案45
年级: 班级: 姓名:
课 题 3.2图案设计 课型 新授课
学习知识点 1.利用平移、轴对称和旋转的这些图形变换中的一种或组合进行图案设计,设计出称心如意的图案.2.通过复习平移、轴对称、旋转的知识,然后利用这些知识让学生 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )开动脑筋,敝开胸怀大胆联想,设计出一幅幅美丽的图案.
学习重点 设计图形
学习难点 如何利用平移、轴对称、旋转等图形变换中的一种或它们的组合得出图案
学 习 过 程学 习 过 程 学习过程-、(学生 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )活动)请同学们独立完成下面的各题. 1.如图,已知线段CD是线段AB平移后的图形,D是B点的对称点,作出线段AB,并回答,AB与CD有什么位置关系. 2.如图,已知线段CD,作出线段CD关于对称轴L的对称线段C′D′,并说明CD与对称线段C′D′之间有什么关系 3.如图,已知线段CD,作出线段CD关于D点旋转90°的旋转后的图形,并说明这两条线段之间有什么关系
点评:1.AB与CD平行且相等;
2.过D点作DE⊥L,垂足为E并延长,使ED′=ED,同理作出C′点,连结C′D′,则CD′就是所求的.CD的延长线与C′D′的延长线相交于一点,这一点在L上并且CD=C′D′.
3.以D点为旋转中心,旋转后CD⊥C′D′,垂足为D,并且CD=C′D. 二、探索新知
请用以上所讲的平移、轴对称、旋转等图形变换中的一种或组合完成下面的图案设计.
例1.(学生活动)学生 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )亲自动手操作题.
按下面的步骤,请每一位同学完成一个别致的图案.
(1)准备一张正三角形纸片(课前准备)(如图a)
(2)把纸片任意撕成两部分(如图b,如图c)
(3)将撕好的如图b沿正三角形的一边作轴对称,得到新的图形.
(4)并将(3)得到的图形以正三角形的一个顶点作为旋转中心旋转,得到如图(d)(如图c)保持不动)
(5)把如图(d)平移到如图(c)的右边,得到如图(e)
(6)对如图(e)进行适当的修饰,使得到一个别致美丽的如图(f)的图案.
老师 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )必要时可以给予一定的指导.
三、巩固练习
教材P78 活动1.
四、应用拓展
例2.(学生 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )活动)请利用线段、三角形、矩形、菱形、圆作为基本图形,绘制一幅反映你身边面貌的图案,并在班级里交流展示.
老师点评:老师 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )点到为止,让学生 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )自由联想,老师 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )也可在黑板上设计一、二图案.
五、归纳小结
本节课应掌握:
利用平移、轴对称和旋转的图形变换中的一种或组合设计图案.
六、布置作业
1.教材P78 活动2 P80 综合运用4、5、6、7.
2.选用作业设计.
作业设计
一、选择题
1.在图所示的4个图案中既包含图形的旋转,还有图形轴对称是( )
2.将三角形绕直线L旋转一周,可以得到如图所示的立体图形的是( )
二、填空题
1.基本图案在轴对称、平移、旋转变化的过程中,图形的______和______都保持不变.
2.如上右图,是由________关系得到的图形.
三、综合提高题
1.(1)图案设计人员在进行图设计时,常常用一个模具板来设计一幅幅美丽漂亮的图案,你能说出用同一模具板设计出的两个图案之间是什么关系吗
(2)现利用同一模具板经过平移、旋转、轴对称设计一个图案,并说明你所表达的意义.
学习后记
岳纸学校教学学案46
年级: 班级: 姓名:
课 题 全等三角形及其性质 课型 新授课
学习知识点 1.知道什么是全等形、全等三角形;2.能熟练找出全等三角形的对应元素,能用符号正确地表示两个三角形全等;3.掌握全等三角形的性质.
学习重点 全等三角形的概念、性质。
学习难点 对应边和对应角的确定
学 习 过 程学 习 过 程 一、全等形、全等三角形的概念阅读课本P2内容,回答课本思考问题,并完成下面填空:1.能够完全重合的两个图形叫做 .全等图形的特征:全等图形的 和 都相同.2.能够完全重合的两个三角形叫做 .二、全等三角形的对应元素及表示阅读课本P3第一个思考及下面两段内容,完成下面填空:1. 平移 翻折 旋转 启示:一个图形经过平移、翻折、旋转后, 变化了,但 、 都没有改变,所以平移、翻折、旋转前后的图形 ,这也是我们通过运动的方法寻全等的一种策略.2.全等三角形的对应元素(1)对应顶点(三个)---重合的顶点 (2)对应边(三条)--- 重合的边 (3)对应角(三个)--- 重合的角请同学们写出上图甲、乙、丙的对应顶点、对应边、对应角图甲: 对应边是: 对应顶点是: 对应角是: 图乙:对应边是: 对应顶点是: 对应角是: 图丙:对应顶点是: 对应边是: 对应角是: 寻找对应元素的规律(1)有公共边的,公共边是对应边;(2)有公共角的,公共角是对应角;(3)有对顶角的,对顶角是对应角;(4)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;(5)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角。3.“全等”用“≌”表示,读作“全等于”如图甲记作:△ABC≌△DEF 读作:△ABC全等于△DEF如图乙记作: 读作: 如图丙记作: 读作: 注意:两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.三、全等三角形的性质阅读课本P3第二个思考及下面内容,完成下面填空:全等三角形的性质:全等三角形的 相等, 相等.练习1.如图1,△OCA≌△OBD,C和B,A和D是对应顶点,说出这两个三角形中相等的边和角. 2.如图2,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.课堂小结本节课你有哪些收获?巩固练习1.下面是两个全等的三角形,按下列图形的位置摆放,指出它们的对应顶点、对应边、对应角.(1) (2) (3)2.如图,△ABE≌△ACD,AB与AC,AD与AE是对应边,已知:∠A=43°,∠B=30°,求∠ADC的大小.课堂检测1.全等用符号 表示,读作: .
2.若△BCE≌△CBF,则∠CBE= , ∠BEC= ,BE= , CE= .
3.判断题
1)全等三角形的对应边相等,对应角相等.( )
2)全等三角形的周长相等,面积也相等. ( )
3)面积相等的三角形是全等三角形. ( )
4)周长相等的三角形是全等三角形. ( )4.如图:△ABC≌△DBF,找出图中的对应边,对应角.答:∠B的对应角是 ,∠C的对应角是 , ∠BAC的对应角是 ; AB的对应边是 ,AC的对应边是 ,BC的对应边是 .课后作业:课本P4习题第1、2题
学习后记
岳纸学校教学学案47
年级: 班级: 姓名:
课 题 全等三角形的识别(一)(SAS) 课型 新授课
学习知识点 会运用“边角边”公理证明三角形全等的简单问题
学习重点 会运用“边角边”公理证明三角形全等的简单问题
学习难点 分清用两边一角证明三角形相似和全等的不同。
把你画的三角形与其他同学画的三角形进行比较,所有的三角形都全等吗?
例2 △ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD.
做一做 如图24.2.7,已知两条线段和一个角,以这两条线段为边,以这个角为其中一条边的对角,画一个三角形.
图24.2.7
把你画的三角形与其他同学画的三角形进行比较,所有的三角形一定都会全等吗?练 习根据题目条件,判断下面的三角形是否全等?
(3) (4)2.点M是等腰梯形ABCD底边AB的中点,△AMD和△BMC全等吗?试说明你的理由?
学习后记
岳纸学校教学学案48、49
年级: 班级: 姓名:
课 题 全等三角形的识别应用 课型 练习课
学习知识点 会运用“边角边”公理证明三角形全等的简单问题
学习重点 会运用“边角边”公理证明三角形全等的简单问题
学习难点 分清用两边一角证明三角形相似和全等的不同。
学 习 过 程学 习 过 程 综合练习:填空: 如图11-2,AB=AD,AC=AE,则可得△ABC≌____其理由是______ 2、如图(1):OA=OD,OB=OC,求证:△ABO≌△DCO 证明: OA=OD OB=OC( ) ____=_____( ) △ABO≌△DCO( )3、如图(2):已知AB=DC,∠ABC=∠DCB,求证:AC=BD 证明:AB=DC,∠ABC=∠DCB ( ) BC=________( ) △BCD≌_______,( )AC=________( ) 如图(1) 如图(2)选择:1、在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么△ABC中与这个角对应的角是( )A ∠A B ∠B C ∠C D ∠B或∠D2、具有下列条件的两个等腰三角形,不能判定它们全等的是( )A 顶角、一腰对应相等 B 底边、一腰对就相等C 两腰对应相等 D 一腰、一底角、一底边对应相等3、△ABC和△A′B′C′边角条件如图:那么这两个三角形( ) A全等 B不全等 C不一定全等 D相似 证明:1、如图,已知∠1=∠2,AO=BO,那么△AOP≌△BOP,为什么?2、已知:AD=BC,∠ADC=∠BCD.求证: ∠BDC=∠ACD.3、如图,AE=DB,BC=EF,BC∥EF,说明△ABC和△DEF全等的理由.4、如图:点M是等腰梯形ABCD底边AB上的中点,则MD与MC的大小有何关系,试说明理由。 5、已知点A、B、C、D在同一条直线上,AB=CD, ∠D=∠ECA,试问:AE与BF的大小关系,并说明理由。6、如图:在△ABC中,AB=AC, ∠BAC=90°,在AB上取点P,边CA的延长线上取点Q,使AP=AQ,边CP与BQ交于点S,求证:△CAP≌△BAQ 7、如图,AB=AD,AC=AE,∠BAE=∠DAC, △ABC与△ADE全等吗?并说明理由。
学习后记
岳纸学校教学学案50、51
年级: 班级: 姓名:
课 题 全等三角形的识别(三)(ASA及AAS) 课型 新授课
学习知识点 会运用“角边角”公理及其推论证明三角形全等的简单问题
学习重点 能灵活运用“角边角”公理及其推论证明三角形全等的简单问题
学习难点
把你画的三角形与其他同学画的进行比较,所有的三角形都全等吗?
由此得到另一个识别全等三角形的简便方法:
例3 如图所示,∠ABC=∠DCB,∠ACB=∠DBC,试说明△ABC≌△DCB.
由此得到另一个识别全等三角形的简便方法:
如果两个三角形的_______及其____分别对应_____,那么这两个三角形全等.简记为(A.A.S.).小结: 如果知道两个三角形的两个角及一条边分别对应相等,这时应该有两种不同的情况: 一种情况是两个角及两角的____(ASA); 另一种情况是两个角及其中一角的___(AAS),两种情况都可以证明三角形全等。如图24.2.8所示.
图24.2.8
学习后记
岳纸学校教学学案52
年级: 班级: 姓名:
课 题 三角形全等的判定(SSS) 课型 新授课
学习知识点 1.理解三边对应相等的两个三角形全等的内容.2.会运用“边边边”条件证明两个三角形全等.3. 会作一个角等于已知角.
学习重点 三边对应相等的两个三角形全等的内容
学习难点 运用“边边边”条件证明两个三角形全等
学 习 过 程学 习 过 程 一、课前准备1. 叫做全等三角形2.全等三角形的 和 相等3.将△ABC沿直线BC平移,得到△DEF,说出你得到的结论,说明理由?如果AB=5, ∠A=55°, ∠B=45°,那么DE= ,∠F= .二、自主探究自主探究三角形全等的条件:阅读课本P6探究2之前,回答下面问题:通过探究(1)只给一个条件对应相等的两个三角形一定全等吗?①只给一条边时 ②只给一个角时; (2)如果给出两个条件画三角形,你能说出有哪几种可能的情况?①给出两个角时;②给出两条边时;③给出一条边和一个角时;(3)由上面的几种情景,两个三角形满足一个或两个条件时,它们一定全等吗?(4)如果两个三角形有三个条件对应相等,这两个三角形全等吗?我们也可以分情况讨论,有哪几种情况? ①我们先来探究两个三角形三个角相等的情况:②画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?③上面的探究反映了什么规律?阅读课本P6-7探究2至例1前,回答下面问题: 的两个三角形全等,简写为“ ”或“ ”.三、例题学习阅读课本P7例1,学习“边边边”证明两个三角形全等的格式.巩固练习1. 如图,AB=AD,BC=CD,求证:(1)△ABC≌△ADC(2)∠B=∠D 证明: (1)在△ABC和△ADC中 (公共边) ∴△ABC≌△ADC( )(2)∵△ABC≌△ADC ∴∠B=∠D( )2.如图,已知AC=FE、BC=DE,点A、D、B、F在一条直线上,AD=FB.要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?证明:四、作一个角等于已知角阅读课本P7最后一段至P8,回答书中问题.课堂小结本节课你有哪些收获?课堂检测如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 证明:课后作业:课本P15习题第1、2题
学 习后 记
岳纸学校教学学案53.54
年级: 班级: 姓名:
课 题 练 习 课型 新授课
学习知识点 对SAS、ASA、AAS、SSS四种判定的应用。
学习重点 对SAS、ASA、AAS、SSS判定的使用。
学习难点 如何适当运用SAS、ASA、AAS、SSS。
学 习 过 程学 习 过 程 填空: 1、如图:D是△ABC的边AB上一点,DE交AC于点E,交CF于点 F,DE=FE,FC∥AB, 求证:AE=CE 证明: FC∥AB( ) ∴∠_____=∠_____,∠_____=∠_____, 又 DE=FE( )∴△AED≌____( )∴AE=CE( ) 2、如图:点B、F、C、E在同一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AB=DE 证明: FB=CE( ) FB+___=CE+__( ) 即:____=____ AB∥ED,AC∥FD ∠ABC=∠_______,∠ACB=∠_______ △ABD≌________,( )AB=DE,( )3、如图:AB=CD,AD=BC,EF过BD的中点O,求证:△OBF≌△ODE 证明:AB=CD,AD=BC( )_________=__________( ) △ABD≌________,( )∠CBD=_______ EF过BD的中点O( )______=__________ 又∠FOB=∠_____( )△OBF≌_______( ) 选择1、下列说法中,正确的是( )A所有的等腰三角形全等B有两边对应相等的两个等腰三角形全等 C有一边对应相等的两个等腰三角形全等D腰和顶角对应相等的两个等腰三角形全等2在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°,∠A′=44°,且AC=A′C′,那么这两个三角形( )A 一定不全等 B 一定全等 C 不一定全等 D 以上都不对3、如图:点E在△ABC外部,点D在BC边上,DE 交AC于F,若∠1=∠2=∠3,AC=AE,则( ) A △ABD≌△AFD B △AFE≌△ADC C △AFE≌△DFC D △ABC≌△ADE 4、在△ABC和△DEF中,条件(1)AB=DE,(2)BC=EF,(3)AC=DF,(4) ∠A=∠D,(5) ∠B=∠E,(6) ∠C=∠F,则下列各组条件中,不能保证△ABC≌△DEF的是( )A(1) (2) (3) B (1) (2) (5) C (1) (3) (5) D(2) (5) (6) 三、证明与计算:根据题目条件,判别下面的两个三角形是否全等,并说明理由. 2、△ABC是等腰三角形,AD、BE分别是∠A、∠B的角平分线,△ABD和△BAE全等吗?试说明理由.3、如图,AB=DE,AC∥DF,BC∥EF,△ABC与△DEF全等吗?说明理由.4、如图,∠1=∠2,∠B=∠D,△ABC和△ADC全等吗?试说明理由。 5、已知: 如图,∠C=∠D,CE=DE.求证: ∠DAB=∠ABC.6、已知: 如图,∠BDA=∠CEA,AE=AD.求证: AB=AC.7、已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC, ∠B=∠C,求证:BD=CE
学习后记
岳纸学校教学学案55
年级: 班级: 姓名:
课 题 直角三角形全等的判定 课型 新授课
学习知识点 1、探索直角三角形全等条件的过程,2、掌握直角三角形全等的条件,并能运用其解决一些实际问题。
学习重点 运用直角三角形全等的条件解决一些实际问题。
学习难点 熟练运用直角三角形全等的条件解决一些实际问题。
学 习 过 程学 习 过 程 Ⅰ.提出问题,复习旧知1、判定两个三角形全等的方法: 、 、 、 ,2、如图,Rt△ABC中,直角边是 、 ,斜边是 3、如图,AB⊥BE于C,DE⊥BE于E,(1)若∠A=∠D,AB=DE,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)(2)若∠A=∠D,BC=EF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)(3)若AB=DE,BC=EF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)(4)若AB=DE,BC=EF,AC=DF则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)Ⅱ.导入新课(一)探索练习:(动手操作):已知线段a ,c (a学习后记
岳纸学校教学学案56
年级: 班级: 姓名:
课 题 角平分线的性质
学习知识点 (1)掌握角平分线的性质定理;(2)能够运用性质定理证明两条线段相等;(3)角平分线的性质定理及它的应用。
学习重点 角平分线的性质定理及它的应用。
学习难点 角平分线的性质定理及它的应用。
学 习 过 程学 习 过 程 一、复习:1、判断两个三角形全等的方法:(1)三边分别相等的两个三角形全等。(2)有两边级其夹角对应相等的两个三角形全等。(3)有两角及其夹边对应相等的两个三角形全等。(4)有两个角及其中一角的对边对应相等的两个三角形全等。(5)有一条直角边和斜边对应相等的两个直角三角形全等。2、练习:根据题目的结论,添加相应的条件。(1)如上图,AB=DE,AC=DF,______=_______,那么根据(SSS)可得(2)如上图,AB=DE,AC=DF,______=_______,那么根据(SAS)可得 (3)如上图,AB=DE,______=______,______=_______,那么根据(ASA)可得(4)如上图,AB=DE,______=______,_______=_______,那么根据(AAS)可得(5)如右图,,_____=_____,_______=_______,那么根据(HL)可得 三、“角平分线上的点到这个角两边的距离相等”小光已经做出了一些步骤,请你帮他补充完整:解: 如右图:已知:__________________,___________________求证:______=_______证明: 归纳:从上面的我们可知道“角平分线上的点到这个角两边的距离相等”这是一个_________(填“真”或“假”)命题。练习:根据上面定理完成书本P 思考。四:把前面的定理反过来可得:“角的内部到角两边的距离相等的点在角的平分线上”已知:如右图,,;并且_______=_______求证:_____是的平分线证明:归纳:从上面的我们可知道“角的内部到角两边的距离相等的点在角的平分线上”这是一个_________(填“真”或“假”)命题。五、练习:A组:1、请你利用尺规作图,画出的平分线B组:请你利用尺规作图在内部找一个点,使这个点到三边距离相等
学 习后 记
岳纸学校教学学案57.58
年级: 班级: 姓名:
课 题 综合练习 课型 习题课
学习知识点 如何判定两直角三角形全等。
学习重点 两直角三角形全等判定的方法。
学习难点 如何使用HL判定定理。
学 习 过 程学 习 过 程 一、填空:两条直角边对应相等的两个直角三角形______,理由是________有一条边和一个锐角对应相等的两个直角三角形_____,理由是______3、如图(1):BA⊥AC,CD∥AB,AB=CE,BC=DE,则△CDE≌______, 理由是_____,且有∠ACB=________,∠ABC=_______,由此可知BC与DE互相__________ 4、如图:AD、A′D′分别是锐角△ABC和△A′B′C′中BC,B′C′边上的高,且AB=A′B′,AD=A′D′,若 使△ABC≌△A′B′C′,需补充条件是______(只需填写一个你认为适当的条件) 二、选择:1、两个直角三角形全等的条件是( )A一锐角对应相等B两锐角对应相等C一条边对应相等D两条边对应相等2、判断下列命题:(1)在Rt△ABC中,两锐角互余(2)有两个锐角不互余的三角形不是直角三角形(3)一条直角边对应相等的两个直角三角形全等(4)有两个锐角对应相等的两个直角三角形全等,其中正确的有( )A 1个 B 2个 C 3个 D 4个3、下列说法正确的有( )(1)两条直角边对应相等的两个直角三角形全等(2)一条边和一个锐角对应相等的两个直角三角形全等(3)两条边对应相等的两个直角三角形全等(4)两个锐角对应相等的两个直角三角形全等。A 1个 B 2个 C 3个 D 4个4、在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠B′,AB=A′B′,那么下列结论中正确的是( )A AC=A′C′ B BC=B′C′ C AC=B′C′D ∠A=∠A′5、下列叙述的图形中,是全等三角形的只有( A 两个含60°角的直角三角形 B 腰对应相等的两个等腰三角形C 有一边相等的两个等边三角形 D 面积相等的两个直角三角形6、如图:△ABC中,∠C=90°,AC=BC,AD平分∠CAB, 交BC于D点,DE⊥AB于点E,且AB=60cm,则△BED的 周长为( ) A 100cm B 80cm C 60cm D 40cm 证明:1、如图:CE⊥AB,DF⊥AB,垂足分别为EF,AC∥DB,且AC=BD,求证:CE=DF2、如图:△ABC是等腰三角形,AB=AC,AD是高,求证(1)BD=DC(2)∠BAD=∠CAD 3、如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,DE=BF,求证(1)AE=CF(2)AB∥CD 4、如图,△ABC中,AD是它的角平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足为E、F,求证:EB=FC 5、如图:在Rt△ABC和Rt△A′B′C′中,∠ACB=∠A′C′B′=90°,CDAB,C′D′A′B′,且CD=C′D′,BC=B′C′,求证:Rt△ABC≌Rt△A′B′C′
学习后记
岳纸学校教学学案59
年级: 班级: 姓名:
课 题 勾股定理(一) 课型 新授课
学习知识点 1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证勾股定理。2.培养在实际生活中发现问题总结规律的意识和能力。
学习重点 勾股定理的内容及证明
学习难点 勾股定理的证明
学 习 过 程学 习 过 程 [课前准备]1、如右图,直角△ABC的主要性质是:∠ACB=90°,(用几何语言表示)⑴两锐角之间的关系: ;⑵若D为斜边中点,则斜边中线与斜边的关系: ;⑶若∠B=30°,则∠B的对边和斜边的关系: 。[新课讲解]今天我们来研究几何上最完美,最丰富的定理。同学们说是什么定理?(板书课题3.6 )什么叫 呢? 。能用数学语言翻译出来吗?学生画图,表达:探究:勾股定理的证明先来看这个图:猜一下我会问什么问题?哪个同学看出来了? (1)赵爽-勾股圆方图 (2)第二证明(3)第三个证明 (4)第四个证明(5)第五个证明[勾股定理的应用]1、已知在Rt△ABC中,∠C=90°,a、b是直角边、c是斜边,由勾股定理可得a,b,c之间的关系为 ,变形可得⑴a2= =(c+b) , a= ,⑵b2= =(c+a) , b= ,⑶c2= ,c= 。总结:在直角三角形中,已知任两边,利用勾股定理可求出 ,对于非直角三角形,常通过作垂线构造出 ,再利用勾股定理解决相关问题。2、求出下列直角三角形中未知边的长度. [达标测试]1、求下图中字母所代表的数值。直角三角形的斜边x长为 ,正方形A面积为 2、如图:所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为7cm,则正方形A,B,C,D的面积之和为 cm2。3、右图阴影部分是一个正方形,求此正方形的面积. [课堂小结]1、勾股定理的具体内容是: 。2、直角三角形中,已知两边求第三边的方法。[拓展提高]如图所示,一棵大树在一次强烈台风中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
岳纸学校教学学案60
年级: 班级: 姓名:
课 题 勾股定理(二) 课型 新授课
学习知识点 1.会用勾股定理进行简单的计算。2.树立数形结合的思想、分类讨论思想。
学习重点 勾股定理的简单计算
学习难点 勾股定理的灵活运用
学 习 过 程学 习 过 程 课堂引入复习勾股定理的文字叙述;勾股定理的符号语言及变形。学习勾股定理重在应用。例题解析1在Rt△ABC,∠C=90°⑴已知a=b=5,求c。⑵已知a=1,c=2, 求b。⑶已知c=17,b=8, 求a。⑷已知a:b=1:2,c=5, 求a。⑸已知b=15,∠A=30°,求a,c。2已知直角三角形的两边长分别为5和12,求第三边。3已知:等边△ABC的边长是6cm。⑴求等边△ABC的高。 ⑵求S△ABC。课堂练习1.填空题⑴在Rt△ABC,∠C=90°,a=8,b=15,则c= 。⑵在Rt△ABC,∠B=90°,a=3,b=4,则c= 。⑶在Rt△ABC,∠C=90°,c=10,a:b=3:4,则a= ,b= 。⑷一个直角三角形的三边为三个连续偶数,则它的三边长分别为 。⑸已知直角三角形的两边长分别为3cm和5cm,,则第三边长为 。⑹已知等边三角形的边长为2cm,则它的高为 ,面积为 。2.已知:如右图,在△ABC中,∠C=60°,AB=,AC=4,AD是BC边上的高,求BC的长。 3.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。拓展提高1.填空题在Rt△ABC,∠C=90°,⑴如果a=7,c=25,则b= 。⑵如果∠A=30°,a=4,则b= 。⑶如果∠A=45°,a=3,则c= 。⑷如果c=10,a-b=2,则b= 。⑸如果a、b、c是连续整数,则a+b+c= 。⑹如果b=8,a:c=3:5,则c= 。2.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC, AB⊥AC,∠B=60°,CD=1cm,求BC的长。3.如(题8图)所示,在Rt△ABC中,∠C=90°,D是BC边上一点,且BD=AD=10,∠ADC=60°,求△ABC面积.
学习后记
岳纸学校教学学案61
年级: 班级: 姓名:
课 题 勾股定理(三) 课型 新授课
学习知识点 1.会用勾股定理解决简单的实际问题。2.树立数形结合的思想。
学习重点 勾股定理的应用
学习难点 实际问题向数学问题的转化
学 习 过 程学 习 过 程 课堂引入勾股定理在实际的生产生活当中有着广泛的应用。勾股定理的发现和使用解决了许多生活中的问题,今天我们就来运用勾股定理解决一些问题,你可以吗?试一试。习题解析如图,△ABC中,∠B=90°,AC=12cm,BC=4cm,D在AC上,且AD=8cm,E在AB上,且△AED的面积是△ABC面积的,求AE和DE的长.课堂练习1.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。2.如图,山坡上两株树木之间的坡面距离是4米,则这两株树之间的垂直距离是 米,水平距离是 米。2题图 3题图 4题图3.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是 。4.如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路一公里造价为300万元,隧道总长为2公里,隧道造价为500万元,AC=80公里,BC=60公里,则改建后可省工程费用是多少?拓展提高1.如图,欲测量松花江的宽度,沿江岸取B、C两点,在江对岸取一点A,使AC垂直江岸,测得BC=50米,∠B=60°,则江面的宽度为 。2.有一个边长为1米正方形的洞口,想用一个圆形盖去盖住这个洞口,则圆形盖半径至少为 米。3.一根32厘米的绳子被折成如图所示的形状钉在P、Q两点,PQ=16厘米,且RP⊥PQ,则RQ= 厘米。4.如下右图,钢索斜拉大桥为等腰三角形,支柱高24米,∠B=∠C=30°,E、F分别为BD、CD中点,试求B、C两点之间的距离,钢索AB和AE的长度。(精确到1米)5.已知,如7图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC上任意一点,求证: BD2+CD2=2AD2.
学习后记
岳纸学校教学学案62
年级: 班级: 姓名:
课 题 勾股定理(四) 课型 新授课
学习知识点 1.会用勾股定理解决较综合的问题。2.树立数形结合的思想。
学习重点 勾股定理的综合应用
学习难点 勾股定理的综合应用
学 习 过 程学 习 过 程 课堂引入复习勾股定理的内容。本节课探究勾股定理的综合应用。习题解析1.在Rt△ABC中,∠C=90°,CD⊥BC于D,∠A=60°,CD=,求线段AB的长。2已知:如右图,△ABC中,AC=4,∠B=45°,∠A=60°,根据题设可知什么?小结:可见解一般三角形的问题常常通过作高转化为直角三角形的问题。3已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。变式训练:在数轴上画出表示的点。课堂练习1.△ABC中,AB=AC=25cm,高AD=20cm,则BC= ,S△ABC= 。2.△ABC中,若∠A=2∠B=3∠C,AC=cm,则∠A= 度,∠B= 度,∠C= 度,BC= ,S△ABC= 。3.△ABC中,∠C=90°,AB=4,BC=,CD⊥AB于D,则AC= ,CD= ,BD= ,AD= ,S△ABC= 。4.已知:如图,△ABC中,AB=26,BC=25,AC=17,求S△ABC。拓展提高1.在Rt△ABC中,∠C=90°,CD⊥BC于D,∠A=60°,CD=,AB= 。2.在Rt△ABC中,∠C=90°,S△ABC=30,c=13,且a<b,则a= ,b= 。3.已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=,求(1)AB的长;(2)S△ABC。4.在数轴上画出表示-的点。5.在△ABC中,∠C=90°,∠A=∠B,则BC:AC:AB是多少 6.如图,在四边形ABCD中,∠BAD=90°,AD=4,AB=3,BC=12,求正方形DCEF的面积.
学习后记
岳纸学校教学学案63
年级: 班级: 姓名:
课 题 勾股定理的逆定理(一) 课型 新授课
学习知识点 1.体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。2.探究勾股定理的逆定理的证明方法。3.理解原命题、逆命题、逆定理的概念及关系。
学习重点 掌握勾股定理的逆定理及证明
学习难点 勾股定理的逆定理的证明
学 习 过 程学 习 过 程 课堂引入⑴怎样判定一个三角形是等腰三角形?⑵怎样判定一个三角形是直角三角形?和等腰三角形的判定进行对比,从勾股定理的逆命题进行猜想。习题解析1说出下列命题的逆命题,这些命题的逆命题成立吗?⑴同旁内角互补,两条直线平行。⑵如果两个实数的平方相等,那么两个实数平方相等。⑶线段垂直平分线上的点到线段两端点的距离相等。⑷直角三角形中30°角所对的直角边等于斜边的一半。2证明:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。3已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,a=n2-1,b=2n,c=n2+1(n>1)求证:∠C=90°。课堂练习1.下列四条线段不能组成直角三角形的是( )A.a=8,b=15,c=17B.a=9,b=12,c=15C.a=,b=,c=D.a:b:c=2:3:42.已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,分别为下列长度,判断该三角形是否是直角三角形?并指出那一个角是直角? ⑴a=,b=,c=; ⑵a=5,b=7,c=9;⑶a=2,b=,c=; ⑷a=5,b=,c=1。拓展提高1.填空题。⑴任何一个命题都有 ,但任何一个定理未必都有 。⑵“两直线平行,内错角相等。”的逆定理是 。⑶在△ABC中,若a2=b2-c2,则△ABC是 三角形, 是直角;若a2<b2-c2,则∠B是 。⑷若在△ABC中,a=m2-n2,b=2mn,c= m2+n2,则△ABC是 三角形。2.若三角形的三边是 ⑴1、、2; ⑵; ⑶32,42,52 ⑷9,40,41;能围成直角三角形的有哪些 3.已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,分别为下列长度,判断该三角形是否是直角三角形?并指出那一个角是直角?⑴a=9,b=41,c=40; ⑵a=15,b=16,c=6;⑶a=2,b=,c=4; ⑷a=5k,b=12k,c=13k(k>0)。4.(m+n)2-1,2(m+n),(m+n)2+1;则构成的是直角三角形的有( )A.2个 B.3个 C.4个 D.5个5.正方形ABCD,E是BC中点,F在AB上,且.求证:.
学习后记
岳纸学校教学学案64
年级: 班级: 姓名:
课 题 勾股定理的逆定理(二) 课型 新授课
学习知识点 1.灵活应用勾股定理及逆定理解决实际问题。2.进一步加深性质定理与判定定理之间关系的认识。
学习重点 灵活应用勾股定理及逆定理解决实际问题
学习难点 灵活应用勾股定理及逆定理解决实际问题
学 习 过 程学 习 过 程 习题解析1.一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,请你试判断这个三角形的形状。2.小强在操场上向东走80m后,又走了60m,再走100m回到原地。小强在操场上向东走了80m后,又走60m的方向是 。3.如图,在操场上竖直立着一根长为2米的测影竿,早晨测得它的影长为4米,中午测得它的影长为1米,则A、B、C三点能否构成直角三角形?为什么?4. 如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截。已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西40°,问:甲巡逻艇的航向?课堂练习1.一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为 ,此三角形的形状为 。2.如图,一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和地面是否垂直,为什么? ⑵3.如图⑵,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量。小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°。4.如图,四边形ABCD中,F为DC的中点,E为BC上一点,且.你能说明∠AFE是直角吗?拓展提高5.若一个三角形的周长12cm,一边长为3cm,其他两边之差为cm,判断这个三角形的形状 6.如图,△ABC的三边分别为 AC=5,BC=12,AB=13,将△ABC沿AD折叠,使AC落在AB上,求DC的长.7. 已知△ABC的三条边长分别为a、b、c,且满足关系:(a+b)2 + c2 = 3ab + c(a+b),试判断△ABC的形状,并说明理由
学习后记
岳纸学校教学学案65
年级: 班级: 姓名:
课 题 勾股定理的逆定理(三) 课型 新授课
学习知识点 1.应用勾股定理的逆定理判断一个三角形是否是直角三角形。 2.灵活应用勾股定理及逆定理解综合题。3.进一步加深性质定理与判定定理之间关系的认识。
学习重点 利用勾股定理及逆定理解综合题
学习难点 利用勾股定理及逆定理解综合题
学 习 过 程学 习 过 程 课堂引入勾股定理和它的逆定理是黄金搭档,经常综合应用来解决一些难度较大的题目。例题解析:1已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c。试判断△ABC的形状。2已知:如图,四边形ABCD,AD∥BC,AB=4,BC=6,CD=5,AD=3。求:四边形ABCD的面积。3已知:在△ABC中,CD是AB边上的高,且CD2=AD·BD。求证:△ABC是直角三角形。 课堂练习:1.若△ABC的三边a、b、c,满足(a-b)(a2+b2-c2)=0,则△ABC是( )A.等腰三角形; B.直角三角形;C.等腰三角形或直角三角形; D.等腰直角三角形。2.若△ABC的三边a、b、c,满足a:b:c=1:1:,试判断△ABC的形状。3.已知:如图,四边形ABCD,AB=1,BC=,CD=,AD=3,且AB⊥BC。求:四边形ABCD的面积。4.已知:在△ABC中,∠ACB=90°,CD⊥AB于D,且CD2=AD·BD。求证:△ABC中是直角三角形。拓展提高:1.若△ABC的三边a、b、c满足a2+b2+c2+50=6a+8b+10c,求△ABC的面积。2.在△ABC中,AB=13cm,AC=24cm,中线BD=5cm。求证:△ABC是等腰三角形。3.已知:如图,∠1=∠2,AD=AE,D为BC上一点,且BD=DC,AC2=AE2+CE2。求证:AB2=AE2+CE2。4.已知△ABC的三边为a、b、c,且a+b=4,ab=1,c=,试判定△ABC的形状。
学习后记
岳纸学校教学学案66、67
年级: 班级: 姓名:
课 题 勾股定理同步练习 课型 习题课
学习知识点 勾股定理及其逆定理的使用。
学习重点 灵活使用勾股定理。
学习难点 逆定理的使用。
学 习 过 程学 习 过 程 第1题. “数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是”,这种说明问题的方式体现的数学思想方法叫做( )A.代入法 B.换元法 C.数形结合 D.分类讨论答案:C第2题. 中,,则 .答案:,第3题. 等腰直角三角形三边之比为( )A. B. C. D.答案:A第4题. 中,三个角,则( )A. B. C. D.答案:C第5题. 等腰直角三角形斜边长为,则斜边上的高为( )A. B. C. D.答案:A第6题. 一个三角形的三边长分别为,,,则这个三角形最大边上的高为( )A. B. C. D.答案:B第7题. 在中,,,,则边上中线的长为( )A. B. C. D.答案:A第8题. 一个等腰直角三角形的面积为,求它的斜边长.答案:第9题. 已知等腰三角形腰长为,底边长为,求底边上的高.答案:第10题. 直角三角形两直角边的长分别为和,则斜边上的高为 ,斜边被高分成两部分的长分别是 .答案:;,第11题. 等腰的腰长为,底边长为,则它的高为 ,面积为 .答案:,第12题. 在中,,,,则 , .答案:,第13题. 如图,边长为的正方形中,为边上一点,于,于,那么 .答案:第14题. 中,,,高,则 .答案:或第15题. 直角三角形的三边长为连续自然数,则它的面积为( )A. B. C. D.答案:A第16题. 如图所示的是房屋人字架的设计图,横梁长为,过屋顶的立柱长为,斜梁,试求斜梁的长.(精确到)答案:第17题. 已知直角三角形的两条直角边,,则斜边 .答案:第18题. 在中,.(1)已知,,则 .(2)已知,,则 .答案:(1)(2)
学习后记
岳纸学校教学学案68
年级: 班级: 姓名:
课 题 习题 课型 练习课
学习知识点 勾股定理及其逆定理的使用。
学习重点 灵活使用勾股定理。
学习难点 逆定理的使用。
B.△ABC是直角三角形,且斜边长为2m
C.△ABC是直角三角形,但斜边长需由n的大小确定 D.由△ABC不是直角三角形 6.已知a,b,c为△ABC三边,且满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状. 7.阅读下列解题过程中:已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判定△ABC的形状. 解:∵a2c2-b2c2=a4-b4 ① ∴c2(a2-b2)=(a2+b2)(a2-b2)② ∴c2=a2+b2 ③ ∴△ABC是直角三角形. 问:上述解题过程,从哪一步开始出现错误?请写出该步的序号:_______,错误的原因为________;本题正确的结论是________. 答案:1.B 2.D 3.C 4.D 解析:注意有两种 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )情况(i)32+42=52, (ii)32+72=42. 5.A 6.解:由已知得(a2-10a+25)+(b2-24b+144)+(c2-26c+169)=0, (a-5)2+(b-12)2+(c-13)2=0, 由于(a-5)2≥0,(b-12)2≥0,(c-13)2≥0. 所以a-5=0,得a=5; b-12=0,得b=12; c-13=0,得c=13. 又因为132=52+122. 即a2+b2=c2, 所以△ABC是直角三角形. 7.③ a2-b2可以为零 △ABC为直角三角形或等腰三角形
学习后记
岳纸学校教学学案69
年级: 班级: 姓名:
课 题 作三角形 已知三边作三角形 课型 新授课
学习知识点 了解尺规作图的含义及其历史背景;会画一个角等于已知角。会画一个角等于已知角;作角平分线;给定边角条件下,求作三角形;
学习重点 尺规作给定边角条件下的三角形
学习难点 作一个角等于已知角、作角平分线与作线段的垂直平分线的作法分析过程。
学 习 过 程学 习 过 程 预习过程:1、如图,使用直尺作图,看图填空. ① ② ③ ④ 过点____和_______作直线AB (2)连结线段___________;(3)以点_______为端点,过点_______作射线___________;(4)延长线段__________到_________,使得BC=2AB.2、如图,使用圆规作图,看图填空:在射线AM上__________线段________=___________.以点______为圆心,以线段______为半径作弧交_________于点___________.以点______为圆心,以任意长为半径作弧,分别交∠AOB两边,交_________于点___________, 交________于点__________.做一做已知线段,如何用直尺(没有刻度)和圆规作使得(三边符合三角形的条件) a b c作法:动脑筋:已知:∠ 如何作一个角:∠AOB,使∠AOB=∠作法:例:试一试:作,使得斜边为,一直角边为()练习:1.如何作出∠AOB的角平分线呢?2.教材第106页第2小题。展示过程:略。反馈练习:1.已知线段AB,用直尺和圆规作线段AB的垂直平分线。2.如图,已知和线段CD,用尺规法求作一点P,使点P到的两边距离相等,且PC=PD。
学习后记
岳纸学校教学学案70
年级: 班级: 姓名:
已知两边及其夹角作三角形 课型 新授课
学习知识点 给出两边及其夹角的条件下,能够利用尺规作三角形。培养学生实际动手能力和合作、自主探究的能力。
学习重点 根据题目的条件作三角形
学习难点 探索作图过程。
学 习 过 程学 习 过 程 [做一做]:已知三角形的两边及其夹角,求作这个三角形.已知:线段a,b及∠α求作:ΔABC,使得BC= a,AB=c,∠ABC=∠α。作法与过程:[动脑筋]你能用尺规作一个等腰三角形,使它的底边长为a,底边上的高为b吗?选一选1、利用尺规不能唯一作出的三角形是( )A、已知三边 B、已知两边及夹角 C、已知两角及夹边 D、已知两边及其中一边的对角2、利用尺规不可作的直角三角形是 ( )A、已知斜边及一条直角边 B、已知两条直角边 C.已知两锐角 D.已知一锐角及一直角边3、以下列线段为边能作三角形的是 ( )A、2厘米、3厘米、5厘米 B、4厘米、4厘米、9厘米C、1厘米、2厘米、 3厘米 D、2厘米、3厘米、4厘米练习:教材第107页练习1、2题。展示过程:略反馈练习:已知:M为∠AOB边上的一点,如图所示,过M作直线CD,使得CD//OA。
学习后记
B
N
B
O
B′
A′
M
O
A
3㎝
3㎝
3cm
45
45
45
300
700
800
300
800
700
A
B
C
D
B
C
D
A
A
B
8
15
C
B
10
C
A
6
81
144
x
225
400
A
A
B
C
D
7cm
F
E
12cm
13cm
A
E
F
BB
C
D
A
D
C
B
G
E
F
O
A
B
D
C
年级: 班级: 姓名:
课 题 3.1旋转 课型 新授课
学习知识点 性质1 对应点到旋转中心的距离相等性质2 对应点与旋转中心的连线所成的角彼此相等,且等于旋转角性质3 旋转不改变图形的形状和大小
学习重点 旋转图形的性质
学习难点 旋转图形的画法
学 习 过 程学 习 过 程 一、课前预习与导学 (1)在平面内,将一个图形绕一个__ _旋转_ _角度,这样的图形运动称为图形的旋转。这个定点为_____。图形绕旋转中心沿着某个方向转过的角成______.(2)旋转前后的图形_____(对应线段__,对应角_____)。(3)对应点到旋转中心的距离________。(4)每一对对应点与旋转中心的连线所成的角彼此_。(5)如图,画出⊿ABC绕点A逆时针旋转90°后的图形。二、新课1、手工制作:制作一个小风车. 2、欣赏日常生活中部分物体的旋转现象. 提出问题:⑴上述情境中的旋转现象有什么共同的特征? ⑵生活还有类似的例子吗? 3、图形的旋转在平面内,将一个图形绕一个 旋转一定的 ,这样的图形运动叫做 。这个定点叫 。旋转的角度称为 。操作活动(1)将一块三角尺ABC绕点C按逆时针方向旋转到DCB的位置 问题: 度量∠ACD与∠BCE的度数,线段AC与DC、BC与EC的长度。你发现了什么?(2)将△ABC绕点O按顺时针方向旋转到△A/ B/C/的位置。 问题:度量∠AO A/、∠BO B/、∠CO C/的度数,线段AO与A/O、BO与B/O、CO与C/O的长度。你发现了什么?三、练一练:⒈ 已知线段AB和点O,按下面的方法画出线段AB绕点O按逆时针方向旋转100°后的图形:⒉ 在图3-4中,画出△ABC按顺时针方向绕点O旋转120度后对应的三角形。四、解决问题1、下列现象中属于旋转的有( )个①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.A.2 B.3 C.4 D.5 2、香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?3、如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个。 4、如图,将点阵中的图形绕点O按逆时针方向旋转900,画出旋转后的图形.5、在等腰直角△ABC中,∠C=900,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转1800,点B落在点B′处,求BB′的长度. 6、已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.五、课堂小结从生活中的旋转现象入手,通过具体的实例认识旋转,探索旋转的性质;通过对具有旋转特征的图形的观察、操作、画图等过程,掌握作图技能。六、布置作业:习题3.1 2、3题
学 习后 记
岳纸学校教学学案45
年级: 班级: 姓名:
课 题 3.2图案设计 课型 新授课
学习知识点 1.利用平移、轴对称和旋转的这些图形变换中的一种或组合进行图案设计,设计出称心如意的图案.2.通过复习平移、轴对称、旋转的知识,然后利用这些知识让学生 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )开动脑筋,敝开胸怀大胆联想,设计出一幅幅美丽的图案.
学习重点 设计图形
学习难点 如何利用平移、轴对称、旋转等图形变换中的一种或它们的组合得出图案
学 习 过 程学 习 过 程 学习过程-、(学生 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )活动)请同学们独立完成下面的各题. 1.如图,已知线段CD是线段AB平移后的图形,D是B点的对称点,作出线段AB,并回答,AB与CD有什么位置关系. 2.如图,已知线段CD,作出线段CD关于对称轴L的对称线段C′D′,并说明CD与对称线段C′D′之间有什么关系 3.如图,已知线段CD,作出线段CD关于D点旋转90°的旋转后的图形,并说明这两条线段之间有什么关系
点评:1.AB与CD平行且相等;
2.过D点作DE⊥L,垂足为E并延长,使ED′=ED,同理作出C′点,连结C′D′,则CD′就是所求的.CD的延长线与C′D′的延长线相交于一点,这一点在L上并且CD=C′D′.
3.以D点为旋转中心,旋转后CD⊥C′D′,垂足为D,并且CD=C′D. 二、探索新知
请用以上所讲的平移、轴对称、旋转等图形变换中的一种或组合完成下面的图案设计.
例1.(学生活动)学生 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )亲自动手操作题.
按下面的步骤,请每一位同学完成一个别致的图案.
(1)准备一张正三角形纸片(课前准备)(如图a)
(2)把纸片任意撕成两部分(如图b,如图c)
(3)将撕好的如图b沿正三角形的一边作轴对称,得到新的图形.
(4)并将(3)得到的图形以正三角形的一个顶点作为旋转中心旋转,得到如图(d)(如图c)保持不动)
(5)把如图(d)平移到如图(c)的右边,得到如图(e)
(6)对如图(e)进行适当的修饰,使得到一个别致美丽的如图(f)的图案.
老师 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )必要时可以给予一定的指导.
三、巩固练习
教材P78 活动1.
四、应用拓展
例2.(学生 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )活动)请利用线段、三角形、矩形、菱形、圆作为基本图形,绘制一幅反映你身边面貌的图案,并在班级里交流展示.
老师点评:老师 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )点到为止,让学生 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )自由联想,老师 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )也可在黑板上设计一、二图案.
五、归纳小结
本节课应掌握:
利用平移、轴对称和旋转的图形变换中的一种或组合设计图案.
六、布置作业
1.教材P78 活动2 P80 综合运用4、5、6、7.
2.选用作业设计.
作业设计
一、选择题
1.在图所示的4个图案中既包含图形的旋转,还有图形轴对称是( )
2.将三角形绕直线L旋转一周,可以得到如图所示的立体图形的是( )
二、填空题
1.基本图案在轴对称、平移、旋转变化的过程中,图形的______和______都保持不变.
2.如上右图,是由________关系得到的图形.
三、综合提高题
1.(1)图案设计人员在进行图设计时,常常用一个模具板来设计一幅幅美丽漂亮的图案,你能说出用同一模具板设计出的两个图案之间是什么关系吗
(2)现利用同一模具板经过平移、旋转、轴对称设计一个图案,并说明你所表达的意义.
学习后记
岳纸学校教学学案46
年级: 班级: 姓名:
课 题 全等三角形及其性质 课型 新授课
学习知识点 1.知道什么是全等形、全等三角形;2.能熟练找出全等三角形的对应元素,能用符号正确地表示两个三角形全等;3.掌握全等三角形的性质.
学习重点 全等三角形的概念、性质。
学习难点 对应边和对应角的确定
学 习 过 程学 习 过 程 一、全等形、全等三角形的概念阅读课本P2内容,回答课本思考问题,并完成下面填空:1.能够完全重合的两个图形叫做 .全等图形的特征:全等图形的 和 都相同.2.能够完全重合的两个三角形叫做 .二、全等三角形的对应元素及表示阅读课本P3第一个思考及下面两段内容,完成下面填空:1. 平移 翻折 旋转 启示:一个图形经过平移、翻折、旋转后, 变化了,但 、 都没有改变,所以平移、翻折、旋转前后的图形 ,这也是我们通过运动的方法寻全等的一种策略.2.全等三角形的对应元素(1)对应顶点(三个)---重合的顶点 (2)对应边(三条)--- 重合的边 (3)对应角(三个)--- 重合的角请同学们写出上图甲、乙、丙的对应顶点、对应边、对应角图甲: 对应边是: 对应顶点是: 对应角是: 图乙:对应边是: 对应顶点是: 对应角是: 图丙:对应顶点是: 对应边是: 对应角是: 寻找对应元素的规律(1)有公共边的,公共边是对应边;(2)有公共角的,公共角是对应角;(3)有对顶角的,对顶角是对应角;(4)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;(5)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角。3.“全等”用“≌”表示,读作“全等于”如图甲记作:△ABC≌△DEF 读作:△ABC全等于△DEF如图乙记作: 读作: 如图丙记作: 读作: 注意:两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.三、全等三角形的性质阅读课本P3第二个思考及下面内容,完成下面填空:全等三角形的性质:全等三角形的 相等, 相等.练习1.如图1,△OCA≌△OBD,C和B,A和D是对应顶点,说出这两个三角形中相等的边和角. 2.如图2,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.课堂小结本节课你有哪些收获?巩固练习1.下面是两个全等的三角形,按下列图形的位置摆放,指出它们的对应顶点、对应边、对应角.(1) (2) (3)2.如图,△ABE≌△ACD,AB与AC,AD与AE是对应边,已知:∠A=43°,∠B=30°,求∠ADC的大小.课堂检测1.全等用符号 表示,读作: .
2.若△BCE≌△CBF,则∠CBE= , ∠BEC= ,BE= , CE= .
3.判断题
1)全等三角形的对应边相等,对应角相等.( )
2)全等三角形的周长相等,面积也相等. ( )
3)面积相等的三角形是全等三角形. ( )
4)周长相等的三角形是全等三角形. ( )4.如图:△ABC≌△DBF,找出图中的对应边,对应角.答:∠B的对应角是 ,∠C的对应角是 , ∠BAC的对应角是 ; AB的对应边是 ,AC的对应边是 ,BC的对应边是 .课后作业:课本P4习题第1、2题
学习后记
岳纸学校教学学案47
年级: 班级: 姓名:
课 题 全等三角形的识别(一)(SAS) 课型 新授课
学习知识点 会运用“边角边”公理证明三角形全等的简单问题
学习重点 会运用“边角边”公理证明三角形全等的简单问题
学习难点 分清用两边一角证明三角形相似和全等的不同。
把你画的三角形与其他同学画的三角形进行比较,所有的三角形都全等吗?
例2 △ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD.
做一做 如图24.2.7,已知两条线段和一个角,以这两条线段为边,以这个角为其中一条边的对角,画一个三角形.
图24.2.7
把你画的三角形与其他同学画的三角形进行比较,所有的三角形一定都会全等吗?练 习根据题目条件,判断下面的三角形是否全等?
(3) (4)2.点M是等腰梯形ABCD底边AB的中点,△AMD和△BMC全等吗?试说明你的理由?
学习后记
岳纸学校教学学案48、49
年级: 班级: 姓名:
课 题 全等三角形的识别应用 课型 练习课
学习知识点 会运用“边角边”公理证明三角形全等的简单问题
学习重点 会运用“边角边”公理证明三角形全等的简单问题
学习难点 分清用两边一角证明三角形相似和全等的不同。
学 习 过 程学 习 过 程 综合练习:填空: 如图11-2,AB=AD,AC=AE,则可得△ABC≌____其理由是______ 2、如图(1):OA=OD,OB=OC,求证:△ABO≌△DCO 证明: OA=OD OB=OC( ) ____=_____( ) △ABO≌△DCO( )3、如图(2):已知AB=DC,∠ABC=∠DCB,求证:AC=BD 证明:AB=DC,∠ABC=∠DCB ( ) BC=________( ) △BCD≌_______,( )AC=________( ) 如图(1) 如图(2)选择:1、在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么△ABC中与这个角对应的角是( )A ∠A B ∠B C ∠C D ∠B或∠D2、具有下列条件的两个等腰三角形,不能判定它们全等的是( )A 顶角、一腰对应相等 B 底边、一腰对就相等C 两腰对应相等 D 一腰、一底角、一底边对应相等3、△ABC和△A′B′C′边角条件如图:那么这两个三角形( ) A全等 B不全等 C不一定全等 D相似 证明:1、如图,已知∠1=∠2,AO=BO,那么△AOP≌△BOP,为什么?2、已知:AD=BC,∠ADC=∠BCD.求证: ∠BDC=∠ACD.3、如图,AE=DB,BC=EF,BC∥EF,说明△ABC和△DEF全等的理由.4、如图:点M是等腰梯形ABCD底边AB上的中点,则MD与MC的大小有何关系,试说明理由。 5、已知点A、B、C、D在同一条直线上,AB=CD, ∠D=∠ECA,试问:AE与BF的大小关系,并说明理由。6、如图:在△ABC中,AB=AC, ∠BAC=90°,在AB上取点P,边CA的延长线上取点Q,使AP=AQ,边CP与BQ交于点S,求证:△CAP≌△BAQ 7、如图,AB=AD,AC=AE,∠BAE=∠DAC, △ABC与△ADE全等吗?并说明理由。
学习后记
岳纸学校教学学案50、51
年级: 班级: 姓名:
课 题 全等三角形的识别(三)(ASA及AAS) 课型 新授课
学习知识点 会运用“角边角”公理及其推论证明三角形全等的简单问题
学习重点 能灵活运用“角边角”公理及其推论证明三角形全等的简单问题
学习难点
把你画的三角形与其他同学画的进行比较,所有的三角形都全等吗?
由此得到另一个识别全等三角形的简便方法:
例3 如图所示,∠ABC=∠DCB,∠ACB=∠DBC,试说明△ABC≌△DCB.
由此得到另一个识别全等三角形的简便方法:
如果两个三角形的_______及其____分别对应_____,那么这两个三角形全等.简记为(A.A.S.).小结: 如果知道两个三角形的两个角及一条边分别对应相等,这时应该有两种不同的情况: 一种情况是两个角及两角的____(ASA); 另一种情况是两个角及其中一角的___(AAS),两种情况都可以证明三角形全等。如图24.2.8所示.
图24.2.8
学习后记
岳纸学校教学学案52
年级: 班级: 姓名:
课 题 三角形全等的判定(SSS) 课型 新授课
学习知识点 1.理解三边对应相等的两个三角形全等的内容.2.会运用“边边边”条件证明两个三角形全等.3. 会作一个角等于已知角.
学习重点 三边对应相等的两个三角形全等的内容
学习难点 运用“边边边”条件证明两个三角形全等
学 习 过 程学 习 过 程 一、课前准备1. 叫做全等三角形2.全等三角形的 和 相等3.将△ABC沿直线BC平移,得到△DEF,说出你得到的结论,说明理由?如果AB=5, ∠A=55°, ∠B=45°,那么DE= ,∠F= .二、自主探究自主探究三角形全等的条件:阅读课本P6探究2之前,回答下面问题:通过探究(1)只给一个条件对应相等的两个三角形一定全等吗?①只给一条边时 ②只给一个角时; (2)如果给出两个条件画三角形,你能说出有哪几种可能的情况?①给出两个角时;②给出两条边时;③给出一条边和一个角时;(3)由上面的几种情景,两个三角形满足一个或两个条件时,它们一定全等吗?(4)如果两个三角形有三个条件对应相等,这两个三角形全等吗?我们也可以分情况讨论,有哪几种情况? ①我们先来探究两个三角形三个角相等的情况:②画出一个三角形,使它的三边长分别为3cm、 4cm、6cm ,把你画的三角形与小组内画的进行比较,它们一定全等吗?③上面的探究反映了什么规律?阅读课本P6-7探究2至例1前,回答下面问题: 的两个三角形全等,简写为“ ”或“ ”.三、例题学习阅读课本P7例1,学习“边边边”证明两个三角形全等的格式.巩固练习1. 如图,AB=AD,BC=CD,求证:(1)△ABC≌△ADC(2)∠B=∠D 证明: (1)在△ABC和△ADC中 (公共边) ∴△ABC≌△ADC( )(2)∵△ABC≌△ADC ∴∠B=∠D( )2.如图,已知AC=FE、BC=DE,点A、D、B、F在一条直线上,AD=FB.要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?证明:四、作一个角等于已知角阅读课本P7最后一段至P8,回答书中问题.课堂小结本节课你有哪些收获?课堂检测如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 证明:课后作业:课本P15习题第1、2题
学 习后 记
岳纸学校教学学案53.54
年级: 班级: 姓名:
课 题 练 习 课型 新授课
学习知识点 对SAS、ASA、AAS、SSS四种判定的应用。
学习重点 对SAS、ASA、AAS、SSS判定的使用。
学习难点 如何适当运用SAS、ASA、AAS、SSS。
学 习 过 程学 习 过 程 填空: 1、如图:D是△ABC的边AB上一点,DE交AC于点E,交CF于点 F,DE=FE,FC∥AB, 求证:AE=CE 证明: FC∥AB( ) ∴∠_____=∠_____,∠_____=∠_____, 又 DE=FE( )∴△AED≌____( )∴AE=CE( ) 2、如图:点B、F、C、E在同一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AB=DE 证明: FB=CE( ) FB+___=CE+__( ) 即:____=____ AB∥ED,AC∥FD ∠ABC=∠_______,∠ACB=∠_______ △ABD≌________,( )AB=DE,( )3、如图:AB=CD,AD=BC,EF过BD的中点O,求证:△OBF≌△ODE 证明:AB=CD,AD=BC( )_________=__________( ) △ABD≌________,( )∠CBD=_______ EF过BD的中点O( )______=__________ 又∠FOB=∠_____( )△OBF≌_______( ) 选择1、下列说法中,正确的是( )A所有的等腰三角形全等B有两边对应相等的两个等腰三角形全等 C有一边对应相等的两个等腰三角形全等D腰和顶角对应相等的两个等腰三角形全等2在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°,∠A′=44°,且AC=A′C′,那么这两个三角形( )A 一定不全等 B 一定全等 C 不一定全等 D 以上都不对3、如图:点E在△ABC外部,点D在BC边上,DE 交AC于F,若∠1=∠2=∠3,AC=AE,则( ) A △ABD≌△AFD B △AFE≌△ADC C △AFE≌△DFC D △ABC≌△ADE 4、在△ABC和△DEF中,条件(1)AB=DE,(2)BC=EF,(3)AC=DF,(4) ∠A=∠D,(5) ∠B=∠E,(6) ∠C=∠F,则下列各组条件中,不能保证△ABC≌△DEF的是( )A(1) (2) (3) B (1) (2) (5) C (1) (3) (5) D(2) (5) (6) 三、证明与计算:根据题目条件,判别下面的两个三角形是否全等,并说明理由. 2、△ABC是等腰三角形,AD、BE分别是∠A、∠B的角平分线,△ABD和△BAE全等吗?试说明理由.3、如图,AB=DE,AC∥DF,BC∥EF,△ABC与△DEF全等吗?说明理由.4、如图,∠1=∠2,∠B=∠D,△ABC和△ADC全等吗?试说明理由。 5、已知: 如图,∠C=∠D,CE=DE.求证: ∠DAB=∠ABC.6、已知: 如图,∠BDA=∠CEA,AE=AD.求证: AB=AC.7、已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC, ∠B=∠C,求证:BD=CE
学习后记
岳纸学校教学学案55
年级: 班级: 姓名:
课 题 直角三角形全等的判定 课型 新授课
学习知识点 1、探索直角三角形全等条件的过程,2、掌握直角三角形全等的条件,并能运用其解决一些实际问题。
学习重点 运用直角三角形全等的条件解决一些实际问题。
学习难点 熟练运用直角三角形全等的条件解决一些实际问题。
学 习 过 程学 习 过 程 Ⅰ.提出问题,复习旧知1、判定两个三角形全等的方法: 、 、 、 ,2、如图,Rt△ABC中,直角边是 、 ,斜边是 3、如图,AB⊥BE于C,DE⊥BE于E,(1)若∠A=∠D,AB=DE,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)(2)若∠A=∠D,BC=EF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)(3)若AB=DE,BC=EF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)(4)若AB=DE,BC=EF,AC=DF则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)Ⅱ.导入新课(一)探索练习:(动手操作):已知线段a ,c (a
岳纸学校教学学案56
年级: 班级: 姓名:
课 题 角平分线的性质
学习知识点 (1)掌握角平分线的性质定理;(2)能够运用性质定理证明两条线段相等;(3)角平分线的性质定理及它的应用。
学习重点 角平分线的性质定理及它的应用。
学习难点 角平分线的性质定理及它的应用。
学 习 过 程学 习 过 程 一、复习:1、判断两个三角形全等的方法:(1)三边分别相等的两个三角形全等。(2)有两边级其夹角对应相等的两个三角形全等。(3)有两角及其夹边对应相等的两个三角形全等。(4)有两个角及其中一角的对边对应相等的两个三角形全等。(5)有一条直角边和斜边对应相等的两个直角三角形全等。2、练习:根据题目的结论,添加相应的条件。(1)如上图,AB=DE,AC=DF,______=_______,那么根据(SSS)可得(2)如上图,AB=DE,AC=DF,______=_______,那么根据(SAS)可得 (3)如上图,AB=DE,______=______,______=_______,那么根据(ASA)可得(4)如上图,AB=DE,______=______,_______=_______,那么根据(AAS)可得(5)如右图,,_____=_____,_______=_______,那么根据(HL)可得 三、“角平分线上的点到这个角两边的距离相等”小光已经做出了一些步骤,请你帮他补充完整:解: 如右图:已知:__________________,___________________求证:______=_______证明: 归纳:从上面的我们可知道“角平分线上的点到这个角两边的距离相等”这是一个_________(填“真”或“假”)命题。练习:根据上面定理完成书本P 思考。四:把前面的定理反过来可得:“角的内部到角两边的距离相等的点在角的平分线上”已知:如右图,,;并且_______=_______求证:_____是的平分线证明:归纳:从上面的我们可知道“角的内部到角两边的距离相等的点在角的平分线上”这是一个_________(填“真”或“假”)命题。五、练习:A组:1、请你利用尺规作图,画出的平分线B组:请你利用尺规作图在内部找一个点,使这个点到三边距离相等
学 习后 记
岳纸学校教学学案57.58
年级: 班级: 姓名:
课 题 综合练习 课型 习题课
学习知识点 如何判定两直角三角形全等。
学习重点 两直角三角形全等判定的方法。
学习难点 如何使用HL判定定理。
学 习 过 程学 习 过 程 一、填空:两条直角边对应相等的两个直角三角形______,理由是________有一条边和一个锐角对应相等的两个直角三角形_____,理由是______3、如图(1):BA⊥AC,CD∥AB,AB=CE,BC=DE,则△CDE≌______, 理由是_____,且有∠ACB=________,∠ABC=_______,由此可知BC与DE互相__________ 4、如图:AD、A′D′分别是锐角△ABC和△A′B′C′中BC,B′C′边上的高,且AB=A′B′,AD=A′D′,若 使△ABC≌△A′B′C′,需补充条件是______(只需填写一个你认为适当的条件) 二、选择:1、两个直角三角形全等的条件是( )A一锐角对应相等B两锐角对应相等C一条边对应相等D两条边对应相等2、判断下列命题:(1)在Rt△ABC中,两锐角互余(2)有两个锐角不互余的三角形不是直角三角形(3)一条直角边对应相等的两个直角三角形全等(4)有两个锐角对应相等的两个直角三角形全等,其中正确的有( )A 1个 B 2个 C 3个 D 4个3、下列说法正确的有( )(1)两条直角边对应相等的两个直角三角形全等(2)一条边和一个锐角对应相等的两个直角三角形全等(3)两条边对应相等的两个直角三角形全等(4)两个锐角对应相等的两个直角三角形全等。A 1个 B 2个 C 3个 D 4个4、在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠B′,AB=A′B′,那么下列结论中正确的是( )A AC=A′C′ B BC=B′C′ C AC=B′C′D ∠A=∠A′5、下列叙述的图形中,是全等三角形的只有( A 两个含60°角的直角三角形 B 腰对应相等的两个等腰三角形C 有一边相等的两个等边三角形 D 面积相等的两个直角三角形6、如图:△ABC中,∠C=90°,AC=BC,AD平分∠CAB, 交BC于D点,DE⊥AB于点E,且AB=60cm,则△BED的 周长为( ) A 100cm B 80cm C 60cm D 40cm 证明:1、如图:CE⊥AB,DF⊥AB,垂足分别为EF,AC∥DB,且AC=BD,求证:CE=DF2、如图:△ABC是等腰三角形,AB=AC,AD是高,求证(1)BD=DC(2)∠BAD=∠CAD 3、如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,DE=BF,求证(1)AE=CF(2)AB∥CD 4、如图,△ABC中,AD是它的角平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足为E、F,求证:EB=FC 5、如图:在Rt△ABC和Rt△A′B′C′中,∠ACB=∠A′C′B′=90°,CDAB,C′D′A′B′,且CD=C′D′,BC=B′C′,求证:Rt△ABC≌Rt△A′B′C′
学习后记
岳纸学校教学学案59
年级: 班级: 姓名:
课 题 勾股定理(一) 课型 新授课
学习知识点 1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证勾股定理。2.培养在实际生活中发现问题总结规律的意识和能力。
学习重点 勾股定理的内容及证明
学习难点 勾股定理的证明
学 习 过 程学 习 过 程 [课前准备]1、如右图,直角△ABC的主要性质是:∠ACB=90°,(用几何语言表示)⑴两锐角之间的关系: ;⑵若D为斜边中点,则斜边中线与斜边的关系: ;⑶若∠B=30°,则∠B的对边和斜边的关系: 。[新课讲解]今天我们来研究几何上最完美,最丰富的定理。同学们说是什么定理?(板书课题3.6 )什么叫 呢? 。能用数学语言翻译出来吗?学生画图,表达:探究:勾股定理的证明先来看这个图:猜一下我会问什么问题?哪个同学看出来了? (1)赵爽-勾股圆方图 (2)第二证明(3)第三个证明 (4)第四个证明(5)第五个证明[勾股定理的应用]1、已知在Rt△ABC中,∠C=90°,a、b是直角边、c是斜边,由勾股定理可得a,b,c之间的关系为 ,变形可得⑴a2= =(c+b) , a= ,⑵b2= =(c+a) , b= ,⑶c2= ,c= 。总结:在直角三角形中,已知任两边,利用勾股定理可求出 ,对于非直角三角形,常通过作垂线构造出 ,再利用勾股定理解决相关问题。2、求出下列直角三角形中未知边的长度. [达标测试]1、求下图中字母所代表的数值。直角三角形的斜边x长为 ,正方形A面积为 2、如图:所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为7cm,则正方形A,B,C,D的面积之和为 cm2。3、右图阴影部分是一个正方形,求此正方形的面积. [课堂小结]1、勾股定理的具体内容是: 。2、直角三角形中,已知两边求第三边的方法。[拓展提高]如图所示,一棵大树在一次强烈台风中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
岳纸学校教学学案60
年级: 班级: 姓名:
课 题 勾股定理(二) 课型 新授课
学习知识点 1.会用勾股定理进行简单的计算。2.树立数形结合的思想、分类讨论思想。
学习重点 勾股定理的简单计算
学习难点 勾股定理的灵活运用
学 习 过 程学 习 过 程 课堂引入复习勾股定理的文字叙述;勾股定理的符号语言及变形。学习勾股定理重在应用。例题解析1在Rt△ABC,∠C=90°⑴已知a=b=5,求c。⑵已知a=1,c=2, 求b。⑶已知c=17,b=8, 求a。⑷已知a:b=1:2,c=5, 求a。⑸已知b=15,∠A=30°,求a,c。2已知直角三角形的两边长分别为5和12,求第三边。3已知:等边△ABC的边长是6cm。⑴求等边△ABC的高。 ⑵求S△ABC。课堂练习1.填空题⑴在Rt△ABC,∠C=90°,a=8,b=15,则c= 。⑵在Rt△ABC,∠B=90°,a=3,b=4,则c= 。⑶在Rt△ABC,∠C=90°,c=10,a:b=3:4,则a= ,b= 。⑷一个直角三角形的三边为三个连续偶数,则它的三边长分别为 。⑸已知直角三角形的两边长分别为3cm和5cm,,则第三边长为 。⑹已知等边三角形的边长为2cm,则它的高为 ,面积为 。2.已知:如右图,在△ABC中,∠C=60°,AB=,AC=4,AD是BC边上的高,求BC的长。 3.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。拓展提高1.填空题在Rt△ABC,∠C=90°,⑴如果a=7,c=25,则b= 。⑵如果∠A=30°,a=4,则b= 。⑶如果∠A=45°,a=3,则c= 。⑷如果c=10,a-b=2,则b= 。⑸如果a、b、c是连续整数,则a+b+c= 。⑹如果b=8,a:c=3:5,则c= 。2.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC, AB⊥AC,∠B=60°,CD=1cm,求BC的长。3.如(题8图)所示,在Rt△ABC中,∠C=90°,D是BC边上一点,且BD=AD=10,∠ADC=60°,求△ABC面积.
学习后记
岳纸学校教学学案61
年级: 班级: 姓名:
课 题 勾股定理(三) 课型 新授课
学习知识点 1.会用勾股定理解决简单的实际问题。2.树立数形结合的思想。
学习重点 勾股定理的应用
学习难点 实际问题向数学问题的转化
学 习 过 程学 习 过 程 课堂引入勾股定理在实际的生产生活当中有着广泛的应用。勾股定理的发现和使用解决了许多生活中的问题,今天我们就来运用勾股定理解决一些问题,你可以吗?试一试。习题解析如图,△ABC中,∠B=90°,AC=12cm,BC=4cm,D在AC上,且AD=8cm,E在AB上,且△AED的面积是△ABC面积的,求AE和DE的长.课堂练习1.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米。2.如图,山坡上两株树木之间的坡面距离是4米,则这两株树之间的垂直距离是 米,水平距离是 米。2题图 3题图 4题图3.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是 。4.如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路一公里造价为300万元,隧道总长为2公里,隧道造价为500万元,AC=80公里,BC=60公里,则改建后可省工程费用是多少?拓展提高1.如图,欲测量松花江的宽度,沿江岸取B、C两点,在江对岸取一点A,使AC垂直江岸,测得BC=50米,∠B=60°,则江面的宽度为 。2.有一个边长为1米正方形的洞口,想用一个圆形盖去盖住这个洞口,则圆形盖半径至少为 米。3.一根32厘米的绳子被折成如图所示的形状钉在P、Q两点,PQ=16厘米,且RP⊥PQ,则RQ= 厘米。4.如下右图,钢索斜拉大桥为等腰三角形,支柱高24米,∠B=∠C=30°,E、F分别为BD、CD中点,试求B、C两点之间的距离,钢索AB和AE的长度。(精确到1米)5.已知,如7图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC上任意一点,求证: BD2+CD2=2AD2.
学习后记
岳纸学校教学学案62
年级: 班级: 姓名:
课 题 勾股定理(四) 课型 新授课
学习知识点 1.会用勾股定理解决较综合的问题。2.树立数形结合的思想。
学习重点 勾股定理的综合应用
学习难点 勾股定理的综合应用
学 习 过 程学 习 过 程 课堂引入复习勾股定理的内容。本节课探究勾股定理的综合应用。习题解析1.在Rt△ABC中,∠C=90°,CD⊥BC于D,∠A=60°,CD=,求线段AB的长。2已知:如右图,△ABC中,AC=4,∠B=45°,∠A=60°,根据题设可知什么?小结:可见解一般三角形的问题常常通过作高转化为直角三角形的问题。3已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。变式训练:在数轴上画出表示的点。课堂练习1.△ABC中,AB=AC=25cm,高AD=20cm,则BC= ,S△ABC= 。2.△ABC中,若∠A=2∠B=3∠C,AC=cm,则∠A= 度,∠B= 度,∠C= 度,BC= ,S△ABC= 。3.△ABC中,∠C=90°,AB=4,BC=,CD⊥AB于D,则AC= ,CD= ,BD= ,AD= ,S△ABC= 。4.已知:如图,△ABC中,AB=26,BC=25,AC=17,求S△ABC。拓展提高1.在Rt△ABC中,∠C=90°,CD⊥BC于D,∠A=60°,CD=,AB= 。2.在Rt△ABC中,∠C=90°,S△ABC=30,c=13,且a<b,则a= ,b= 。3.已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=,求(1)AB的长;(2)S△ABC。4.在数轴上画出表示-的点。5.在△ABC中,∠C=90°,∠A=∠B,则BC:AC:AB是多少 6.如图,在四边形ABCD中,∠BAD=90°,AD=4,AB=3,BC=12,求正方形DCEF的面积.
学习后记
岳纸学校教学学案63
年级: 班级: 姓名:
课 题 勾股定理的逆定理(一) 课型 新授课
学习知识点 1.体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。2.探究勾股定理的逆定理的证明方法。3.理解原命题、逆命题、逆定理的概念及关系。
学习重点 掌握勾股定理的逆定理及证明
学习难点 勾股定理的逆定理的证明
学 习 过 程学 习 过 程 课堂引入⑴怎样判定一个三角形是等腰三角形?⑵怎样判定一个三角形是直角三角形?和等腰三角形的判定进行对比,从勾股定理的逆命题进行猜想。习题解析1说出下列命题的逆命题,这些命题的逆命题成立吗?⑴同旁内角互补,两条直线平行。⑵如果两个实数的平方相等,那么两个实数平方相等。⑶线段垂直平分线上的点到线段两端点的距离相等。⑷直角三角形中30°角所对的直角边等于斜边的一半。2证明:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。3已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,a=n2-1,b=2n,c=n2+1(n>1)求证:∠C=90°。课堂练习1.下列四条线段不能组成直角三角形的是( )A.a=8,b=15,c=17B.a=9,b=12,c=15C.a=,b=,c=D.a:b:c=2:3:42.已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,分别为下列长度,判断该三角形是否是直角三角形?并指出那一个角是直角? ⑴a=,b=,c=; ⑵a=5,b=7,c=9;⑶a=2,b=,c=; ⑷a=5,b=,c=1。拓展提高1.填空题。⑴任何一个命题都有 ,但任何一个定理未必都有 。⑵“两直线平行,内错角相等。”的逆定理是 。⑶在△ABC中,若a2=b2-c2,则△ABC是 三角形, 是直角;若a2<b2-c2,则∠B是 。⑷若在△ABC中,a=m2-n2,b=2mn,c= m2+n2,则△ABC是 三角形。2.若三角形的三边是 ⑴1、、2; ⑵; ⑶32,42,52 ⑷9,40,41;能围成直角三角形的有哪些 3.已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,分别为下列长度,判断该三角形是否是直角三角形?并指出那一个角是直角?⑴a=9,b=41,c=40; ⑵a=15,b=16,c=6;⑶a=2,b=,c=4; ⑷a=5k,b=12k,c=13k(k>0)。4.(m+n)2-1,2(m+n),(m+n)2+1;则构成的是直角三角形的有( )A.2个 B.3个 C.4个 D.5个5.正方形ABCD,E是BC中点,F在AB上,且.求证:.
学习后记
岳纸学校教学学案64
年级: 班级: 姓名:
课 题 勾股定理的逆定理(二) 课型 新授课
学习知识点 1.灵活应用勾股定理及逆定理解决实际问题。2.进一步加深性质定理与判定定理之间关系的认识。
学习重点 灵活应用勾股定理及逆定理解决实际问题
学习难点 灵活应用勾股定理及逆定理解决实际问题
学 习 过 程学 习 过 程 习题解析1.一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,请你试判断这个三角形的形状。2.小强在操场上向东走80m后,又走了60m,再走100m回到原地。小强在操场上向东走了80m后,又走60m的方向是 。3.如图,在操场上竖直立着一根长为2米的测影竿,早晨测得它的影长为4米,中午测得它的影长为1米,则A、B、C三点能否构成直角三角形?为什么?4. 如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截。已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西40°,问:甲巡逻艇的航向?课堂练习1.一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为 ,此三角形的形状为 。2.如图,一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和地面是否垂直,为什么? ⑵3.如图⑵,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量。小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°。4.如图,四边形ABCD中,F为DC的中点,E为BC上一点,且.你能说明∠AFE是直角吗?拓展提高5.若一个三角形的周长12cm,一边长为3cm,其他两边之差为cm,判断这个三角形的形状 6.如图,△ABC的三边分别为 AC=5,BC=12,AB=13,将△ABC沿AD折叠,使AC落在AB上,求DC的长.7. 已知△ABC的三条边长分别为a、b、c,且满足关系:(a+b)2 + c2 = 3ab + c(a+b),试判断△ABC的形状,并说明理由
学习后记
岳纸学校教学学案65
年级: 班级: 姓名:
课 题 勾股定理的逆定理(三) 课型 新授课
学习知识点 1.应用勾股定理的逆定理判断一个三角形是否是直角三角形。 2.灵活应用勾股定理及逆定理解综合题。3.进一步加深性质定理与判定定理之间关系的认识。
学习重点 利用勾股定理及逆定理解综合题
学习难点 利用勾股定理及逆定理解综合题
学 习 过 程学 习 过 程 课堂引入勾股定理和它的逆定理是黄金搭档,经常综合应用来解决一些难度较大的题目。例题解析:1已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c。试判断△ABC的形状。2已知:如图,四边形ABCD,AD∥BC,AB=4,BC=6,CD=5,AD=3。求:四边形ABCD的面积。3已知:在△ABC中,CD是AB边上的高,且CD2=AD·BD。求证:△ABC是直角三角形。 课堂练习:1.若△ABC的三边a、b、c,满足(a-b)(a2+b2-c2)=0,则△ABC是( )A.等腰三角形; B.直角三角形;C.等腰三角形或直角三角形; D.等腰直角三角形。2.若△ABC的三边a、b、c,满足a:b:c=1:1:,试判断△ABC的形状。3.已知:如图,四边形ABCD,AB=1,BC=,CD=,AD=3,且AB⊥BC。求:四边形ABCD的面积。4.已知:在△ABC中,∠ACB=90°,CD⊥AB于D,且CD2=AD·BD。求证:△ABC中是直角三角形。拓展提高:1.若△ABC的三边a、b、c满足a2+b2+c2+50=6a+8b+10c,求△ABC的面积。2.在△ABC中,AB=13cm,AC=24cm,中线BD=5cm。求证:△ABC是等腰三角形。3.已知:如图,∠1=∠2,AD=AE,D为BC上一点,且BD=DC,AC2=AE2+CE2。求证:AB2=AE2+CE2。4.已知△ABC的三边为a、b、c,且a+b=4,ab=1,c=,试判定△ABC的形状。
学习后记
岳纸学校教学学案66、67
年级: 班级: 姓名:
课 题 勾股定理同步练习 课型 习题课
学习知识点 勾股定理及其逆定理的使用。
学习重点 灵活使用勾股定理。
学习难点 逆定理的使用。
学 习 过 程学 习 过 程 第1题. “数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是”,这种说明问题的方式体现的数学思想方法叫做( )A.代入法 B.换元法 C.数形结合 D.分类讨论答案:C第2题. 中,,则 .答案:,第3题. 等腰直角三角形三边之比为( )A. B. C. D.答案:A第4题. 中,三个角,则( )A. B. C. D.答案:C第5题. 等腰直角三角形斜边长为,则斜边上的高为( )A. B. C. D.答案:A第6题. 一个三角形的三边长分别为,,,则这个三角形最大边上的高为( )A. B. C. D.答案:B第7题. 在中,,,,则边上中线的长为( )A. B. C. D.答案:A第8题. 一个等腰直角三角形的面积为,求它的斜边长.答案:第9题. 已知等腰三角形腰长为,底边长为,求底边上的高.答案:第10题. 直角三角形两直角边的长分别为和,则斜边上的高为 ,斜边被高分成两部分的长分别是 .答案:;,第11题. 等腰的腰长为,底边长为,则它的高为 ,面积为 .答案:,第12题. 在中,,,,则 , .答案:,第13题. 如图,边长为的正方形中,为边上一点,于,于,那么 .答案:第14题. 中,,,高,则 .答案:或第15题. 直角三角形的三边长为连续自然数,则它的面积为( )A. B. C. D.答案:A第16题. 如图所示的是房屋人字架的设计图,横梁长为,过屋顶的立柱长为,斜梁,试求斜梁的长.(精确到)答案:第17题. 已知直角三角形的两条直角边,,则斜边 .答案:第18题. 在中,.(1)已知,,则 .(2)已知,,则 .答案:(1)(2)
学习后记
岳纸学校教学学案68
年级: 班级: 姓名:
课 题 习题 课型 练习课
学习知识点 勾股定理及其逆定理的使用。
学习重点 灵活使用勾股定理。
学习难点 逆定理的使用。
B.△ABC是直角三角形,且斜边长为2m
C.△ABC是直角三角形,但斜边长需由n的大小确定 D.由△ABC不是直角三角形 6.已知a,b,c为△ABC三边,且满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状. 7.阅读下列解题过程中:已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判定△ABC的形状. 解:∵a2c2-b2c2=a4-b4 ① ∴c2(a2-b2)=(a2+b2)(a2-b2)② ∴c2=a2+b2 ③ ∴△ABC是直角三角形. 问:上述解题过程,从哪一步开始出现错误?请写出该步的序号:_______,错误的原因为________;本题正确的结论是________. 答案:1.B 2.D 3.C 4.D 解析:注意有两种 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )情况(i)32+42=52, (ii)32+72=42. 5.A 6.解:由已知得(a2-10a+25)+(b2-24b+144)+(c2-26c+169)=0, (a-5)2+(b-12)2+(c-13)2=0, 由于(a-5)2≥0,(b-12)2≥0,(c-13)2≥0. 所以a-5=0,得a=5; b-12=0,得b=12; c-13=0,得c=13. 又因为132=52+122. 即a2+b2=c2, 所以△ABC是直角三角形. 7.③ a2-b2可以为零 △ABC为直角三角形或等腰三角形
学习后记
岳纸学校教学学案69
年级: 班级: 姓名:
课 题 作三角形 已知三边作三角形 课型 新授课
学习知识点 了解尺规作图的含义及其历史背景;会画一个角等于已知角。会画一个角等于已知角;作角平分线;给定边角条件下,求作三角形;
学习重点 尺规作给定边角条件下的三角形
学习难点 作一个角等于已知角、作角平分线与作线段的垂直平分线的作法分析过程。
学 习 过 程学 习 过 程 预习过程:1、如图,使用直尺作图,看图填空. ① ② ③ ④ 过点____和_______作直线AB (2)连结线段___________;(3)以点_______为端点,过点_______作射线___________;(4)延长线段__________到_________,使得BC=2AB.2、如图,使用圆规作图,看图填空:在射线AM上__________线段________=___________.以点______为圆心,以线段______为半径作弧交_________于点___________.以点______为圆心,以任意长为半径作弧,分别交∠AOB两边,交_________于点___________, 交________于点__________.做一做已知线段,如何用直尺(没有刻度)和圆规作使得(三边符合三角形的条件) a b c作法:动脑筋:已知:∠ 如何作一个角:∠AOB,使∠AOB=∠作法:例:试一试:作,使得斜边为,一直角边为()练习:1.如何作出∠AOB的角平分线呢?2.教材第106页第2小题。展示过程:略。反馈练习:1.已知线段AB,用直尺和圆规作线段AB的垂直平分线。2.如图,已知和线段CD,用尺规法求作一点P,使点P到的两边距离相等,且PC=PD。
学习后记
岳纸学校教学学案70
年级: 班级: 姓名:
已知两边及其夹角作三角形 课型 新授课
学习知识点 给出两边及其夹角的条件下,能够利用尺规作三角形。培养学生实际动手能力和合作、自主探究的能力。
学习重点 根据题目的条件作三角形
学习难点 探索作图过程。
学 习 过 程学 习 过 程 [做一做]:已知三角形的两边及其夹角,求作这个三角形.已知:线段a,b及∠α求作:ΔABC,使得BC= a,AB=c,∠ABC=∠α。作法与过程:[动脑筋]你能用尺规作一个等腰三角形,使它的底边长为a,底边上的高为b吗?选一选1、利用尺规不能唯一作出的三角形是( )A、已知三边 B、已知两边及夹角 C、已知两角及夹边 D、已知两边及其中一边的对角2、利用尺规不可作的直角三角形是 ( )A、已知斜边及一条直角边 B、已知两条直角边 C.已知两锐角 D.已知一锐角及一直角边3、以下列线段为边能作三角形的是 ( )A、2厘米、3厘米、5厘米 B、4厘米、4厘米、9厘米C、1厘米、2厘米、 3厘米 D、2厘米、3厘米、4厘米练习:教材第107页练习1、2题。展示过程:略反馈练习:已知:M为∠AOB边上的一点,如图所示,过M作直线CD,使得CD//OA。
学习后记
B
N
B
O
B′
A′
M
O
A
3㎝
3㎝
3cm
45
45
45
300
700
800
300
800
700
A
B
C
D
B
C
D
A
A
B
8
15
C
B
10
C
A
6
81
144
x
225
400
A
A
B
C
D
7cm
F
E
12cm
13cm
A
E
F
BB
C
D
A
D
C
B
G
E
F
O
A
B
D
C
同课章节目录
