4.1.3认识三角形(3) 课件(共19张PPT)
文档属性
| 名称 | 4.1.3认识三角形(3) 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 711.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-22 10:59:39 | ||
图片预览






文档简介
4.1.3认识三角形(3)
第四章 三角形
2021年春北师大版七年级数学下册
学习目标
1.了解三角形的角平分线、中线的概念并掌握其性质,会用工具准确画出三角形的角平分线、中线;(重点)
2. 学会用数学知识解决实际问题的能力,发展应 用和自主探究意识,并培养学生的动手实践能力与 合作精神;(难点)
三角形的三个边有什么关系?
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边.
A
B
C
a
b
c
即 a+b>c
a-b<c
因此 a-b<c<a+b
新课导入
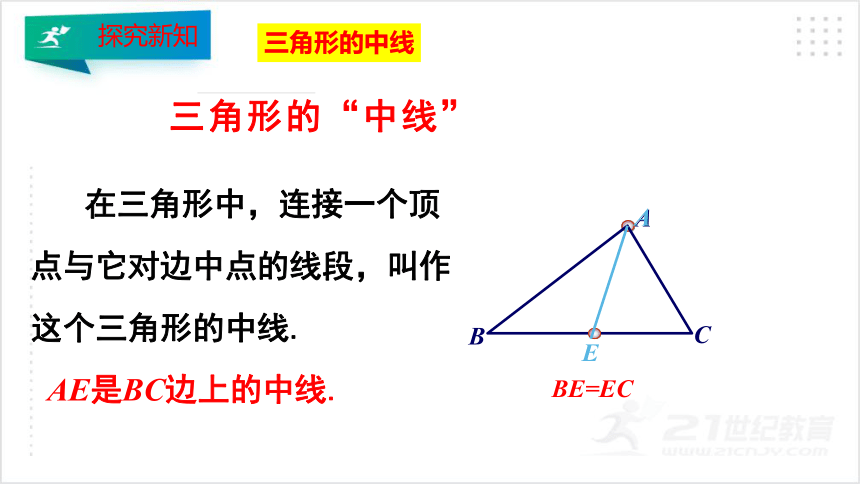
在三角形中,连接一个顶点与它对边中点的线段,叫作这个三角形的中线.
AE是BC边上的中线.
三角形的“中线”
B
A
C
A
BE=EC
E
三角形的中线
探究新知
(1)在纸上画出一个锐角三角形,确定它的中线.
你有什么方法?它有多少条中线?它们有怎样的位置关系?
议一议
三条中线,
交于一点
探究新知
(2)钝角三角形和直角三角形的中线又是怎样的?
折一折,画一画,并与同伴交流.
三角形的三条中线交于一点,这个交点就是三角形的重心.
要点归纳
探究新知
三角形的角平分线
思考
在一张薄纸上任意画一个三角形,你能设法画出它的一个内角的平分线吗?你能通过折纸的方法得到它吗?
探究新知
B
A
C
用量角器画最简便,用圆规也能.
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A的平分线.
A
B
C
A
D
探究新知
三角形的角平分线的定义:
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
1
2
A
B
C
D
注意:“三角形的角平分线”是一条线段.
∠1=∠2
探究新知
每人准备锐角三角形、钝角三角形和直角三角
形纸片各一个.
(1) 你能分别画出这三个三角形的三条角平分线吗?
(2) 你能用折纸的办法得到它们吗?
(3) 在每个三角形中,这三条角平分线之间有怎样的
位置关系 ?
做一做
探究新知
三角形的三条角平分线交于同一点.
三角形角平分线的性质
探究新知
1、AD是ΔABC的角平分线(如图),
那么∠BAC= ∠BAD;
2、AE是ΔABC的中线(如图),
那么那么BC= BE。
A
D
C
B
A
B
C
E
2
2
课堂练习
2. 在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
7cm
课堂练习
解:∵AD是△ABC的角平分线,∠BAC=68°,
∴∠DAC=∠BAD=34°.
在△ABD中,
∠B+∠ADB+∠BAD=180°,
∴∠ADB=180°-∠B-∠BAD
=180°-36°-34°=110°.
3.如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,求∠ADB的度数.
A
B
D
C
课堂练习
4.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC
的周长为25cm,求ΔADC的周长.
A
D
B
C
解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)=25-5=20cm.
课堂练习
5.如图,AE是 △ABC的角平分线.已知∠B=45°,
∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:∵AE是△ABC的角平分线,
∵ ∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,∴∠BAE=37.5°.
∵∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE= ∠BAC.
课堂练习
三角形中几条重要线段
角平分线:平分内角且与三角形对边相交的线段.
中线:连接三角形的顶点与对边中点的线段.
课堂小结
https://www.21cnjy.com/help/help_extract.php
第四章 三角形
2021年春北师大版七年级数学下册
学习目标
1.了解三角形的角平分线、中线的概念并掌握其性质,会用工具准确画出三角形的角平分线、中线;(重点)
2. 学会用数学知识解决实际问题的能力,发展应 用和自主探究意识,并培养学生的动手实践能力与 合作精神;(难点)
三角形的三个边有什么关系?
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边.
A
B
C
a
b
c
即 a+b>c
a-b<c
因此 a-b<c<a+b
新课导入
在三角形中,连接一个顶点与它对边中点的线段,叫作这个三角形的中线.
AE是BC边上的中线.
三角形的“中线”
B
A
C
A
BE=EC
E
三角形的中线
探究新知
(1)在纸上画出一个锐角三角形,确定它的中线.
你有什么方法?它有多少条中线?它们有怎样的位置关系?
议一议
三条中线,
交于一点
探究新知
(2)钝角三角形和直角三角形的中线又是怎样的?
折一折,画一画,并与同伴交流.
三角形的三条中线交于一点,这个交点就是三角形的重心.
要点归纳
探究新知
三角形的角平分线
思考
在一张薄纸上任意画一个三角形,你能设法画出它的一个内角的平分线吗?你能通过折纸的方法得到它吗?
探究新知
B
A
C
用量角器画最简便,用圆规也能.
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A的平分线.
A
B
C
A
D
探究新知
三角形的角平分线的定义:
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
1
2
A
B
C
D
注意:“三角形的角平分线”是一条线段.
∠1=∠2
探究新知
每人准备锐角三角形、钝角三角形和直角三角
形纸片各一个.
(1) 你能分别画出这三个三角形的三条角平分线吗?
(2) 你能用折纸的办法得到它们吗?
(3) 在每个三角形中,这三条角平分线之间有怎样的
位置关系 ?
做一做
探究新知
三角形的三条角平分线交于同一点.
三角形角平分线的性质
探究新知
1、AD是ΔABC的角平分线(如图),
那么∠BAC= ∠BAD;
2、AE是ΔABC的中线(如图),
那么那么BC= BE。
A
D
C
B
A
B
C
E
2
2
课堂练习
2. 在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
7cm
课堂练习
解:∵AD是△ABC的角平分线,∠BAC=68°,
∴∠DAC=∠BAD=34°.
在△ABD中,
∠B+∠ADB+∠BAD=180°,
∴∠ADB=180°-∠B-∠BAD
=180°-36°-34°=110°.
3.如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,求∠ADB的度数.
A
B
D
C
课堂练习
4.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC
的周长为25cm,求ΔADC的周长.
A
D
B
C
解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)=25-5=20cm.
课堂练习
5.如图,AE是 △ABC的角平分线.已知∠B=45°,
∠C=60°,求∠BAE和∠AEB的度数.
A
B
C
E
解:∵AE是△ABC的角平分线,
∵ ∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,∴∠BAE=37.5°.
∵∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE= ∠BAC.
课堂练习
三角形中几条重要线段
角平分线:平分内角且与三角形对边相交的线段.
中线:连接三角形的顶点与对边中点的线段.
课堂小结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
