1.3.1函数的单调性与导数

(共26张PPT)
4、对数函数的导数:
5、指数函数的导数:
3、三角函数 ：
1、常函数：(C)/ 0, (c为常数)；
2、幂函数 ： (xn)/ nxn 1
一、复习回顾：基本初等函数的导数公式
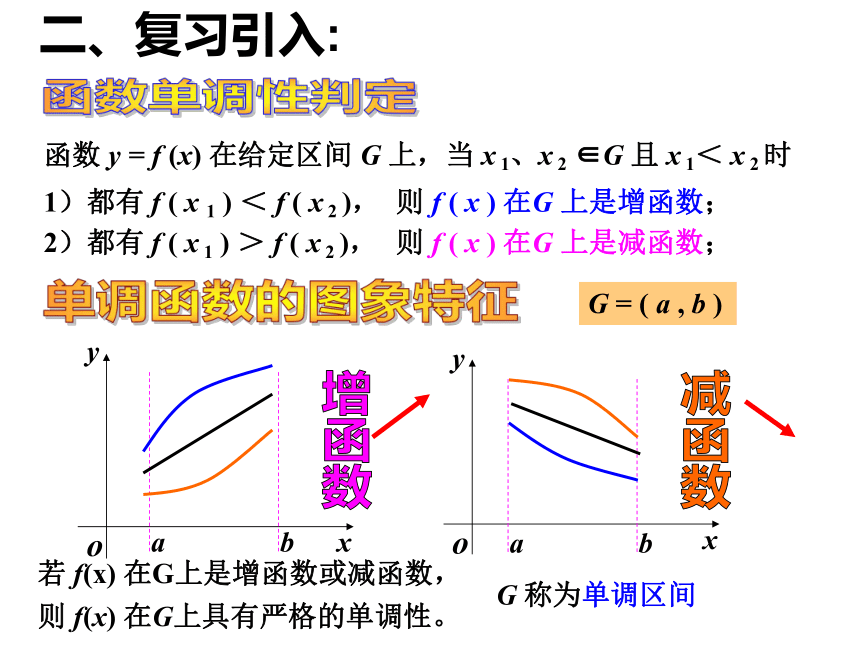
函数 y = f (x) 在给定区间 G 上，当 x 1、x 2 ∈G 且 x 1＜ x 2 时
y
x
o
a
b
y
x
o
a
b
1）都有 f ( x 1 ) ＜ f ( x 2 )，
则 f ( x ) 在G 上是增函数；
2）都有 f ( x 1 ) ＞ f ( x 2 )，
则 f ( x ) 在G 上是减函数；
若 f(x) 在G上是增函数或减函数，
则 f(x) 在G上具有严格的单调性。
G 称为单调区间
G = ( a , b )
二、复习引入:
o
y
x
y
o
x
1
o
y
x
1
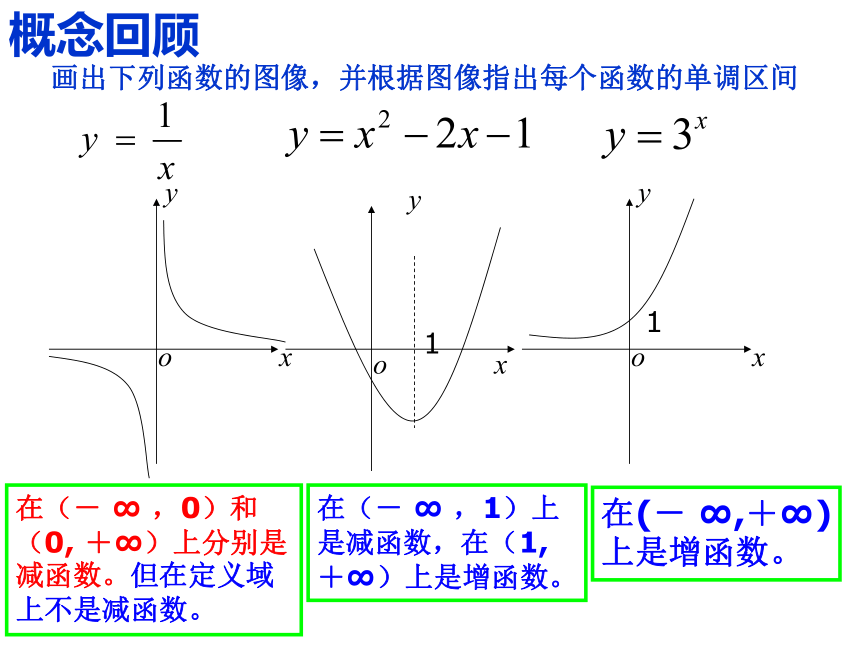
在（－ ∞ ，0）和（0, ＋∞）上分别是减函数。但在定义域上不是减函数。
在（－ ∞ ，1）上是减函数，在（1, ＋∞）上是增函数。
在(－ ∞,＋∞)上是增函数。
概念回顾
画出下列函数的图像，并根据图像指出每个函数的单调区间
(1)函数的单调性也叫函数的增减性；
(2)函数的单调性是对某个区间而言的，它是个局部概
念。这个区间是定义域的子集。
(3)单调区间：针对自变量x而言的。
若函数在此区间上是增函数，则为单调递增区间；
若函数在此区间上是减函数，则为单调递减区间。
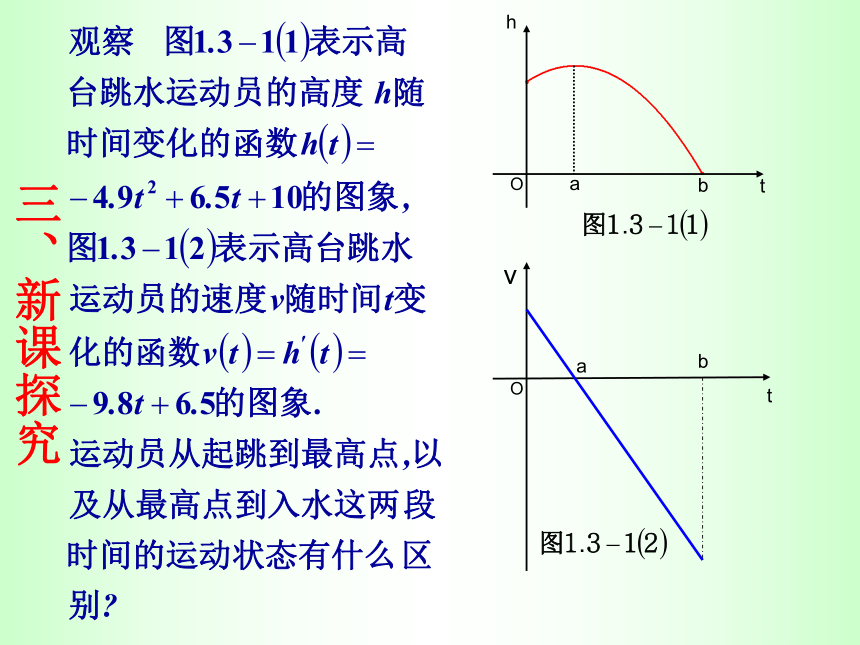
以前,我们用定义来判断函数的单调性.在假设x1三、新课探究
如果函数在某个区间上恒有f‘(x)=0，那么函数在这个区间上是常数函数。
-cosx-1
单调递减
6x2+6x-24
1、求可导函数f(x)单调区间的步骤：
(1)求f’(x)；
(2)解不等式f’(x)>0(或f’(x)<0)；
(3)确认并指出递增区间(或递减区间).
2、证明可导函数f(x)在(a,b)内的单调性的方法：
(1)求f’(x);
(2)确认f’(x)在(a,b)内的符号;
(3)作出结论.
总结提炼
注意：在最后写单调区间时，不等式的解的各段连续区间用“和”或“，”隔开，千万不能用“U”.
练习
判断下列函数的单调性, 并求出单调区间:
练习
2.函数 的图象如图所示, 试画出导函数图像的大致形状.
3.讨论二次函数 的单调区间.
解:
由 , 得 , 即函数 的递增区间是 ; 相应地, 函数的递减区间是
由 , 得 , 即函数 的递增区间是 ; 相应地, 函数的递减区间是
练习
4.求证: 函数 在 内是减函数.
解:
由 , 解得 , 所以函数 的递减区间是 , 即函数 在 内是减函数.
练习