4.1.2 认识三角形(2)课件(共21张PPT)
文档属性
| 名称 | 4.1.2 认识三角形(2)课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 745.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-22 18:54:09 | ||
图片预览




文档简介
4.1.2认识三角形(2)
第四章 三角形
2021年春北师大版七年级数学下册
学习目标
1.掌握三角形按边分类的方法,能够判定三角形
是否为特殊三角形;(重点)
2.探索并掌握三角形三边之间的关系,运用三角形
三边关系解决有关问题.(难点)
1、顶点:
用一个大写字母:表示如A、B、C
2、边:
边AB(c),边BC(a),边AC(b)
3、角(内角):相邻两边 的夹角∠A,∠B,∠C
5、对角:
对边:
∠C的对边是BA
BC边的对角是∠A
三角形的相关概念
A
B
C
a
b
c
4、表示:三角形:△ABC(无顺序)直角三角形:Rt?ABC
6.三角形三个内角的和等于180度.
∠A+∠B+∠C=180°
直角三角形的两个锐角互余
当∠C=90°时, ∠A+∠B=90°
新课导入
三角形按角的大小关系,可分为:
直角三角形
锐角三角形
钝角三角形
三角形
三角形若按边来分类,可分为哪几类?
新课导入
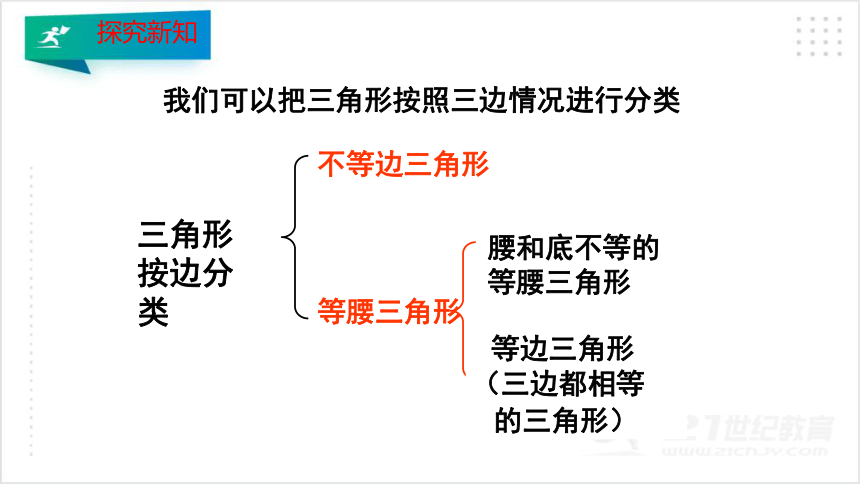
三角形按边分类
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
你能找出下列三角形各自的特点吗?
三边均不相等
有两条边相等
三条边均相等
探究新知
三条边各不相等的三角形叫作不等边三角形 ;
有两条边相等的三角形叫作等腰三角形;
三条边都相等的三角形叫作等边三角形.
等边三角形和等腰三角形之间有什么关系?
总结归纳
三角形按边分类
不等边三角形
等腰三角形
我们可以把三角形按照三边情况进行分类
腰和底不等的等腰三角形
等边三角形(三边都相等
的三角形)
探究新知
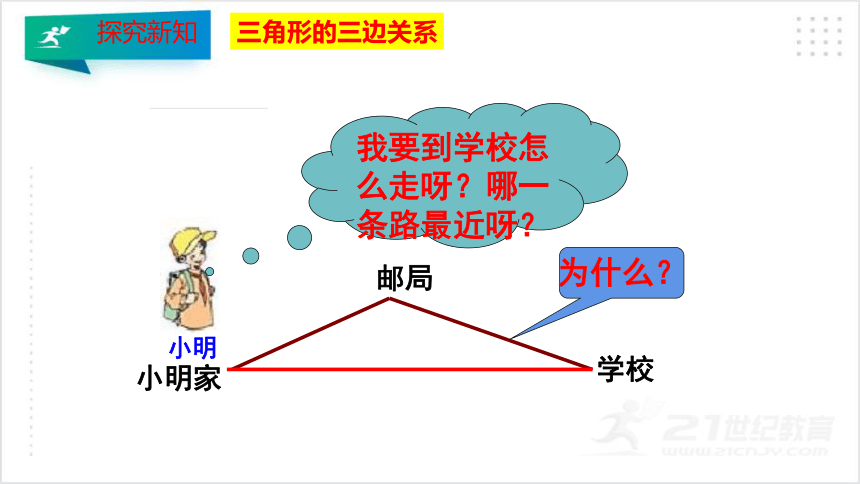
三角形的三边关系
小明
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
小明家
探究新知
A
B
C
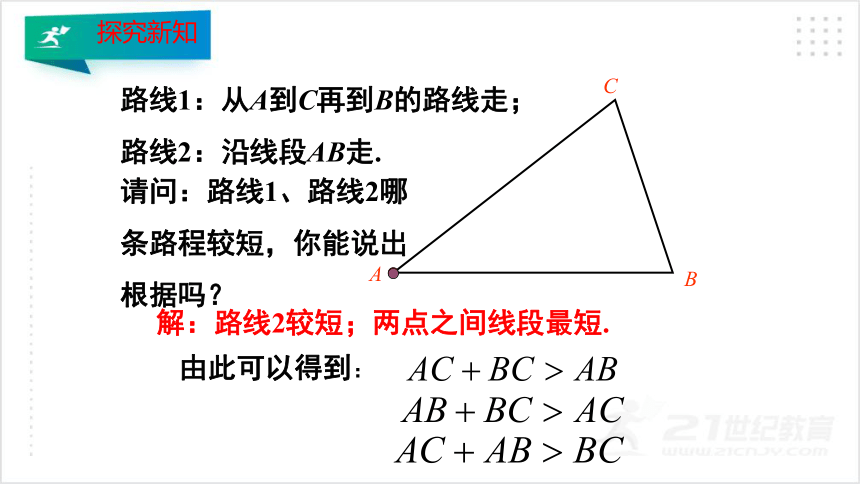
路线1:从A到C再到B的路线走;
路线2:沿线段AB走.
请问:路线1、路线2哪条路程较短,你能说出根据吗?
解:路线2较短;两点之间线段最短.
由此可以得到:
探究新知
归纳总结
三角形两边的和大于第三边.
三角形两边的差小于第三边.
议一议
1.在同一个三角形中,任意两边之和与第三边有什么
大小关系?
2.在同一个三角形中,任意两边之差与第三边有什么
大小关系?
3.三角形三边有怎样的不等关系?
通过动手实验同学们可以得到哪些结论?理由是什么?
例1 有两根长度分别为5cm和8cm的木棒,用长度
为2cm的木棒与它们能摆成三角形吗?为什么?长
度为13cm的木棒呢?
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
归纳
例题讲解
1.下面每组数分别是三根小棒的长度,用它们能摆成三角形吗?
1. 3cm 5cm 4cm ( )
2. 8cm 7cm 15cm ( )
3. 5cm 5cm 11cm ( )
╳
╳
√
课堂练习
(2)等边三角形是特殊的等腰三角形.( )
(1)一个钝角三角形一定不是等腰三角形.( )
(3)等腰三角形的腰和底一定不相等.( )
(5)直角三角形一定不是等腰三角形.( )
2.判断:
√
×
×
(4)等边三角形是锐角三角形.( )
×
√
课堂练习
3. 下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗?实际摆一摆,验证你的结论。
(1)3cm, 4cm, 5cm ; (2)8cm, 7cm, 15cm
(3) 13cm, 12cm, 20cm; (4)5cm, 5cm, 11cm
4.现有长度分别为1cm,2cm,3cm,4cm,5cm的五条线段,从其中选三条线段为边可以构成 个的不同的三角形。
(1)(3)
3
课堂练习
6.如果等腰三角形的一边长是4cm,另一边长是9cm,
则这个等腰三角形的周长为________.
5.如果等腰三角形的一边长是5cm,另一边长是8cm,
则这个等腰三角形的周长为______________.
22cm
18cm或21cm
课堂练习
7.小颖要制作一个三角形木架,现有两根长度为 8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
∵x为偶数,∴小颖有5种选法.
第三根木棒的长度可以是4cm,6cm,8cm,10cm,12cm.
解:设第三根木棒长为xcm,有8-5<x<8+5,
即3<x<13.
课堂练习
8.已知等腰三角形的周长为18cm,如果一边长
等于4cm,求另两边的长?
解:若底边长为4cm,设腰长为x cm,
则2x+4=18,解得x=7.
若一条腰长为4cm,设底边长为x cm,
则2×4+x=18,解得x=10.
因为4+4<10,所以4cm为腰不能构成三角形.
所以三角形另外两个边长都是7cm.
课堂练习
9. 在△ABC中,a=4,b=2,若第三边c的 长是偶数,求c的长?
解: ∵a-b< c< a+b
∴2 又∵第三边c的长是偶数
∴c=4
课堂练习
三角形中边的关系
三角形按边分类
不等边三角形
等腰三角形(包括等边三角形)
三角形的三边关系
任意两边之和大于第三边
任意两边之差小于第三边
课堂小结
https://www.21cnjy.com/help/help_extract.php
第四章 三角形
2021年春北师大版七年级数学下册
学习目标
1.掌握三角形按边分类的方法,能够判定三角形
是否为特殊三角形;(重点)
2.探索并掌握三角形三边之间的关系,运用三角形
三边关系解决有关问题.(难点)
1、顶点:
用一个大写字母:表示如A、B、C
2、边:
边AB(c),边BC(a),边AC(b)
3、角(内角):相邻两边 的夹角∠A,∠B,∠C
5、对角:
对边:
∠C的对边是BA
BC边的对角是∠A
三角形的相关概念
A
B
C
a
b
c
4、表示:三角形:△ABC(无顺序)直角三角形:Rt?ABC
6.三角形三个内角的和等于180度.
∠A+∠B+∠C=180°
直角三角形的两个锐角互余
当∠C=90°时, ∠A+∠B=90°
新课导入
三角形按角的大小关系,可分为:
直角三角形
锐角三角形
钝角三角形
三角形
三角形若按边来分类,可分为哪几类?
新课导入
三角形按边分类
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
你能找出下列三角形各自的特点吗?
三边均不相等
有两条边相等
三条边均相等
探究新知
三条边各不相等的三角形叫作不等边三角形 ;
有两条边相等的三角形叫作等腰三角形;
三条边都相等的三角形叫作等边三角形.
等边三角形和等腰三角形之间有什么关系?
总结归纳
三角形按边分类
不等边三角形
等腰三角形
我们可以把三角形按照三边情况进行分类
腰和底不等的等腰三角形
等边三角形(三边都相等
的三角形)
探究新知
三角形的三边关系
小明
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
小明家
探究新知
A
B
C
路线1:从A到C再到B的路线走;
路线2:沿线段AB走.
请问:路线1、路线2哪条路程较短,你能说出根据吗?
解:路线2较短;两点之间线段最短.
由此可以得到:
探究新知
归纳总结
三角形两边的和大于第三边.
三角形两边的差小于第三边.
议一议
1.在同一个三角形中,任意两边之和与第三边有什么
大小关系?
2.在同一个三角形中,任意两边之差与第三边有什么
大小关系?
3.三角形三边有怎样的不等关系?
通过动手实验同学们可以得到哪些结论?理由是什么?
例1 有两根长度分别为5cm和8cm的木棒,用长度
为2cm的木棒与它们能摆成三角形吗?为什么?长
度为13cm的木棒呢?
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
归纳
例题讲解
1.下面每组数分别是三根小棒的长度,用它们能摆成三角形吗?
1. 3cm 5cm 4cm ( )
2. 8cm 7cm 15cm ( )
3. 5cm 5cm 11cm ( )
╳
╳
√
课堂练习
(2)等边三角形是特殊的等腰三角形.( )
(1)一个钝角三角形一定不是等腰三角形.( )
(3)等腰三角形的腰和底一定不相等.( )
(5)直角三角形一定不是等腰三角形.( )
2.判断:
√
×
×
(4)等边三角形是锐角三角形.( )
×
√
课堂练习
3. 下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗?实际摆一摆,验证你的结论。
(1)3cm, 4cm, 5cm ; (2)8cm, 7cm, 15cm
(3) 13cm, 12cm, 20cm; (4)5cm, 5cm, 11cm
4.现有长度分别为1cm,2cm,3cm,4cm,5cm的五条线段,从其中选三条线段为边可以构成 个的不同的三角形。
(1)(3)
3
课堂练习
6.如果等腰三角形的一边长是4cm,另一边长是9cm,
则这个等腰三角形的周长为________.
5.如果等腰三角形的一边长是5cm,另一边长是8cm,
则这个等腰三角形的周长为______________.
22cm
18cm或21cm
课堂练习
7.小颖要制作一个三角形木架,现有两根长度为 8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
∵x为偶数,∴小颖有5种选法.
第三根木棒的长度可以是4cm,6cm,8cm,10cm,12cm.
解:设第三根木棒长为xcm,有8-5<x<8+5,
即3<x<13.
课堂练习
8.已知等腰三角形的周长为18cm,如果一边长
等于4cm,求另两边的长?
解:若底边长为4cm,设腰长为x cm,
则2x+4=18,解得x=7.
若一条腰长为4cm,设底边长为x cm,
则2×4+x=18,解得x=10.
因为4+4<10,所以4cm为腰不能构成三角形.
所以三角形另外两个边长都是7cm.
课堂练习
9. 在△ABC中,a=4,b=2,若第三边c的 长是偶数,求c的长?
解: ∵a-b< c< a+b
∴2
∴c=4
课堂练习
三角形中边的关系
三角形按边分类
不等边三角形
等腰三角形(包括等边三角形)
三角形的三边关系
任意两边之和大于第三边
任意两边之差小于第三边
课堂小结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
