2.3.2 平行线的性质 课件(共24张PPT)
文档属性
| 名称 | 2.3.2 平行线的性质 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-22 00:00:00 | ||
图片预览







文档简介
第3节 平行线的性质
(第2课时)
第二章 相交线与平行线
2021年春北师大版七年级数学下册
1 复习巩固判定直线平行和平行线性质的相关知识.(重点)
2 学会书写表达几何推理论证过程.(难点)
学习目标
平行线的性质1:
两条平行直线被第三条直线所截, 同位角相等.
性质2:两条平行直线被第三条直线所截,内错角相等.
性质3: 两条平行直线被第三条直线所截,同旁内角互补.
新课导入
平行线性质的应用
根据图,回答下列问题:
(1)若∠1=∠2,则可以判定哪两条直线平行?根据是什么?
解:∠1与∠2是内错角,若∠1=∠2,则根据 “内错角相等,两直线平行”,可得BF//CE.
A
B
C
D
F
M
E
3
2
1
探究新知
(2)若∠2=∠M,则可以判定哪两条直线平行?根据是什么?
∠2与∠M 是同位角,若∠2=∠M,则根据 “同位角相等,两直线平行”,可得AM//BF.
A
B
C
D
F
M
E
3
2
1
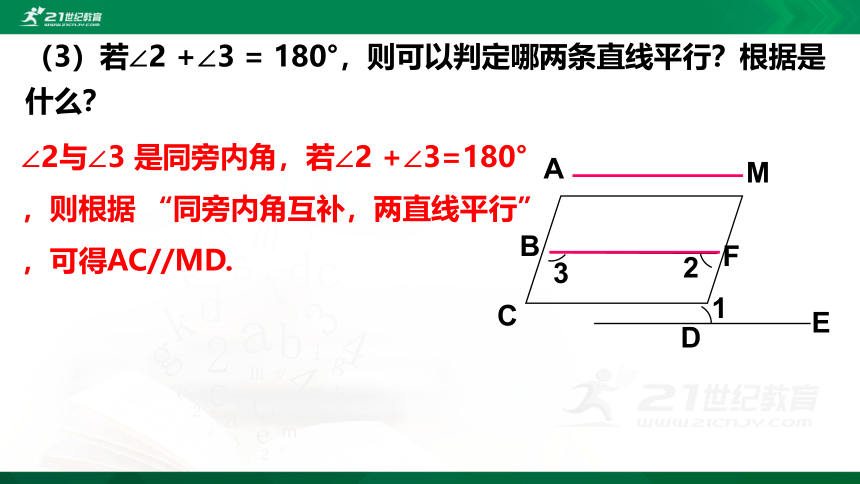
(3)若∠2 +∠3 = 180°,则可以判定哪两条直线平行?根据是什么?
∠2与∠3 是同旁内角,若∠2 +∠3=180°,则根据 “同旁内角互补,两直线平行”,可得AC//MD.
A
B
C
D
F
M
E
3
2
1
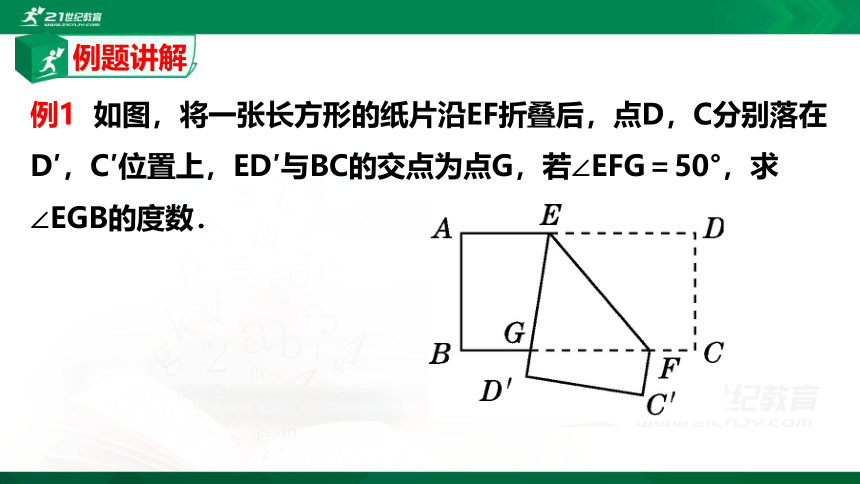
例1 如图,将一张长方形的纸片沿EF折叠后,点D,C分别落在D′,C′位置上,ED′与BC的交点为点G,若∠EFG=50°,求∠EGB的度数.
例题讲解
解:因为四边形ABCD是长方形(已知),
所以∠A=∠B=90°(长方形的定义).
所以∠A+∠B=180°.
所以AD∥BC(同旁内角互补,两直线平行).
所以∠DEF=∠EFG(两直线平行,内错角相等).
因为∠EFG=50°(已知),
所以∠DEF=50°(等量代换).
因为∠DEF=∠D′EF(折叠的性质),
所以∠D′EF=50°(等量代换).
所以∠AEG=180°-∠DEF-∠D′EF=80°(平角的定义).
又因为AD∥BC,
所以∠AEG+∠EGB=180°(两直线平行,同旁内角互补),
即∠EGB=180°-∠AEG=180°-80°=100°.
平行线判定的应用
1 平行线的判定方法:
(1)两条直线被另一条直线截得的同位角相等;
(2)两条直线同平行于第三条直线;
(3)在同一平面内,两条直线同垂直于第三条直线.
2 判定两直线平行的方法:
(1)利用平行线的定义判定;
(2)利用“同位角相等,两直线平行”判定;
(3)利用“第三直线”(平行或垂直)判定.
探究新知
例2 如图, AB∥CD,如果 ∠1 =∠2,那么 EF 与 AB 平行吗?说说你的理由.
例题讲解
解:因为 ∠1 = ∠2,
根据“内错角相等,两直线平行” ,
所以 EF∥CD.
又因为 AB∥CD,
根据“平行于同一条直线的两条直线平行” ,
所以 EF∥AB.
平行线性质和判定的综合应用
例3 如图,已知直线 a∥b,直线 c∥d,∠1=107°,求∠2,∠3 的度数.
2
1
3
a
b
c
d
解:因为a∥b,
根据“两直线平行,内错角相等”,
所以 ∠2 = ∠1 = 107° .
因为 c∥d,
根据“两直线平行,同旁内角互补”,
所以 ∠1 + ∠3 = 180° ,
所以 ∠3 = 180°-∠1 = 180°-107° = 73° .
探究新知
平行线的三个特征:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的三个判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
归纳小结
想一想
两条直线被第三条直线所截,如果同位角相等,那么内错角相等吗?同旁内角互补吗?
m
n
l
3
4
2
1
1 如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于( )
A.35°
B.40°
C.45°
D.50°
课堂练习
2 如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )
A.70°
B.60°
C.55°
D.50°
3 如图,若∠A+∠ABC=180°,则下列结论正确的是( )
A.∠1=∠2
B.∠2=∠3
C.∠1=∠3
D.∠2=∠4
4 如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是( )
A.80°
B.85°
C.95°
D.100°
5 如图所示,a//b,∠1=∠2,∠3=40°,则∠4 等于( )
A. 40° B. 50° C. 60° D. 70°
a
b
1
2
3
4
6 如图,已知∠1=105°, ∠2=75°你能判断a∥b吗?
1 同位角相等,两直线平行.
2 内错角相等,两直线平行.
3 同旁内角互补,两直线平行.
4 两直线平行, 同位角相等.
5 两直线平行, 内错角相等.
6 两直线平行, 同旁内角互补.
课堂小结
谢谢聆听
(第2课时)
第二章 相交线与平行线
2021年春北师大版七年级数学下册
1 复习巩固判定直线平行和平行线性质的相关知识.(重点)
2 学会书写表达几何推理论证过程.(难点)
学习目标
平行线的性质1:
两条平行直线被第三条直线所截, 同位角相等.
性质2:两条平行直线被第三条直线所截,内错角相等.
性质3: 两条平行直线被第三条直线所截,同旁内角互补.
新课导入
平行线性质的应用
根据图,回答下列问题:
(1)若∠1=∠2,则可以判定哪两条直线平行?根据是什么?
解:∠1与∠2是内错角,若∠1=∠2,则根据 “内错角相等,两直线平行”,可得BF//CE.
A
B
C
D
F
M
E
3
2
1
探究新知
(2)若∠2=∠M,则可以判定哪两条直线平行?根据是什么?
∠2与∠M 是同位角,若∠2=∠M,则根据 “同位角相等,两直线平行”,可得AM//BF.
A
B
C
D
F
M
E
3
2
1
(3)若∠2 +∠3 = 180°,则可以判定哪两条直线平行?根据是什么?
∠2与∠3 是同旁内角,若∠2 +∠3=180°,则根据 “同旁内角互补,两直线平行”,可得AC//MD.
A
B
C
D
F
M
E
3
2
1
例1 如图,将一张长方形的纸片沿EF折叠后,点D,C分别落在D′,C′位置上,ED′与BC的交点为点G,若∠EFG=50°,求∠EGB的度数.
例题讲解
解:因为四边形ABCD是长方形(已知),
所以∠A=∠B=90°(长方形的定义).
所以∠A+∠B=180°.
所以AD∥BC(同旁内角互补,两直线平行).
所以∠DEF=∠EFG(两直线平行,内错角相等).
因为∠EFG=50°(已知),
所以∠DEF=50°(等量代换).
因为∠DEF=∠D′EF(折叠的性质),
所以∠D′EF=50°(等量代换).
所以∠AEG=180°-∠DEF-∠D′EF=80°(平角的定义).
又因为AD∥BC,
所以∠AEG+∠EGB=180°(两直线平行,同旁内角互补),
即∠EGB=180°-∠AEG=180°-80°=100°.
平行线判定的应用
1 平行线的判定方法:
(1)两条直线被另一条直线截得的同位角相等;
(2)两条直线同平行于第三条直线;
(3)在同一平面内,两条直线同垂直于第三条直线.
2 判定两直线平行的方法:
(1)利用平行线的定义判定;
(2)利用“同位角相等,两直线平行”判定;
(3)利用“第三直线”(平行或垂直)判定.
探究新知
例2 如图, AB∥CD,如果 ∠1 =∠2,那么 EF 与 AB 平行吗?说说你的理由.
例题讲解
解:因为 ∠1 = ∠2,
根据“内错角相等,两直线平行” ,
所以 EF∥CD.
又因为 AB∥CD,
根据“平行于同一条直线的两条直线平行” ,
所以 EF∥AB.
平行线性质和判定的综合应用
例3 如图,已知直线 a∥b,直线 c∥d,∠1=107°,求∠2,∠3 的度数.
2
1
3
a
b
c
d
解:因为a∥b,
根据“两直线平行,内错角相等”,
所以 ∠2 = ∠1 = 107° .
因为 c∥d,
根据“两直线平行,同旁内角互补”,
所以 ∠1 + ∠3 = 180° ,
所以 ∠3 = 180°-∠1 = 180°-107° = 73° .
探究新知
平行线的三个特征:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的三个判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
归纳小结
想一想
两条直线被第三条直线所截,如果同位角相等,那么内错角相等吗?同旁内角互补吗?
m
n
l
3
4
2
1
1 如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于( )
A.35°
B.40°
C.45°
D.50°
课堂练习
2 如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )
A.70°
B.60°
C.55°
D.50°
3 如图,若∠A+∠ABC=180°,则下列结论正确的是( )
A.∠1=∠2
B.∠2=∠3
C.∠1=∠3
D.∠2=∠4
4 如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是( )
A.80°
B.85°
C.95°
D.100°
5 如图所示,a//b,∠1=∠2,∠3=40°,则∠4 等于( )
A. 40° B. 50° C. 60° D. 70°
a
b
1
2
3
4
6 如图,已知∠1=105°, ∠2=75°你能判断a∥b吗?
1 同位角相等,两直线平行.
2 内错角相等,两直线平行.
3 同旁内角互补,两直线平行.
4 两直线平行, 同位角相等.
5 两直线平行, 内错角相等.
6 两直线平行, 同旁内角互补.
课堂小结
谢谢聆听
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
