2020-2021学年人教五四版八年级下册数学期末练习试题(word含解析)
文档属性
| 名称 | 2020-2021学年人教五四版八年级下册数学期末练习试题(word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 315.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-22 12:42:34 | ||
图片预览


文档简介
2020-2021学年人教五四版八年级下册数学期末练习试题
一.选择题(共10小题,满分30分,每小题3分)
1.下列方程中,是一元二次方程的是( )
A.ax2+bx+c=0
B.x2+=1
C.x2﹣1=0
D.2x+3y﹣5=0
2.下列各组数中,能构成直角三角形的是( )
A.4,5,6
B.1,1,
C.6,8,11
D.5,12,23
3.已知点(﹣3,y1)、(﹣1,3)、(2,y2)在一次函数y=kx+5的图象上,则y1,y2,3的大小关系正确( )
A.3<y2<y1
B.y1<3<y2
C.y2<y1<3
D.y2<3<y1
4.已知平行四边形ABCD中,∠B=4∠A,则∠C=( )
A.18°
B.36°
C.72°
D.144°
5.对于函数y=﹣2x+2,下列结论:①当x>1时,y<0;②它的图象经过第一、二、三象限;③它的图象必经过点(﹣2,2);④y的值随x的增大而增大,其中正确结论的个数是( )
A.1
B.2
C.3
D.4
6.如图是一次函数y1=kx+b与y2=x+a的图象,则不等式kx﹣x<a﹣b的解集是( )
A.x<3
B.x>3
C.x<a+b
D.x>a﹣b
7.以三角形三边中点和三角形三个顶点能画出平行四边形有( )个
A.1
B.2
C.3
D.4
8.下列命题是真命题的个数为( )
①两条直线被第三条直线所截,内错角相等.
②三角形的内角和是180°.
③在同一平面内,平行于同一条直线的两条直线平行.
④相等的角是对顶角.
⑤两点之间,线段最短.
A.2
B.3
C.4
D.5
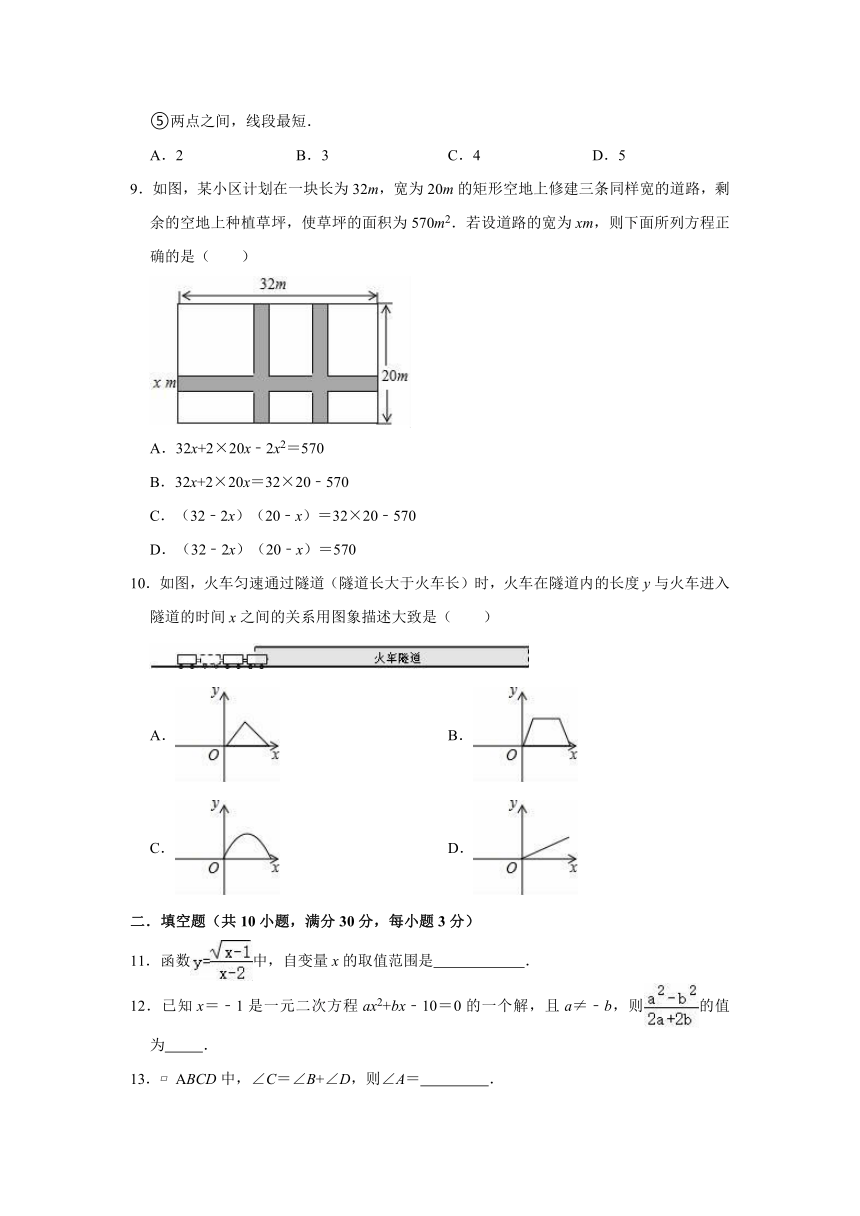
9.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是( )
A.32x+2×20x﹣2x2=570
B.32x+2×20x=32×20﹣570
C.(32﹣2x)(20﹣x)=32×20﹣570
D.(32﹣2x)(20﹣x)=570
10.如图,火车匀速通过隧道(隧道长大于火车长)时,火车在隧道内的长度y与火车进入隧道的时间x之间的关系用图象描述大致是( )
A.
B.
C.
D.
二.填空题(共10小题,满分30分,每小题3分)
11.函数中,自变量x的取值范围是
.
12.已知x=﹣1是一元二次方程ax2+bx﹣10=0的一个解,且a≠﹣b,则的值为
.
13.?ABCD中,∠C=∠B+∠D,则∠A=
.
14.已知正比例函数经过点P(a,3a)(其中a为常数,a≠0),则该正比例函数解析式为
.
15.如图,已知菱形ABCD的对角线AC、BD交于点O,OC=2cm,∠ABO=30°,则菱形
ABCD的面积是
.
16.已知直线y=kx+4,该直线与两坐标轴围成的三角形面积为8,那么k的值是
.
17.已知一等腰三角形的一边长为5,另一边长为方程x2﹣8x+12=0的根,该等腰三角形的周长为
.
18.如图,在等腰直角△ABC中,AB=AC,点D在边BC上,∠ADB=60°,将△ADC沿AD翻折后点C落在点C′,则AB与BC′的比值为
.
19.如图,在矩形ABCD中,AD=6,AB=4,∠BAD的平分线交BC于点E,则DE=
.
20.如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是
.
三.解答题(共7小题,满分60分)
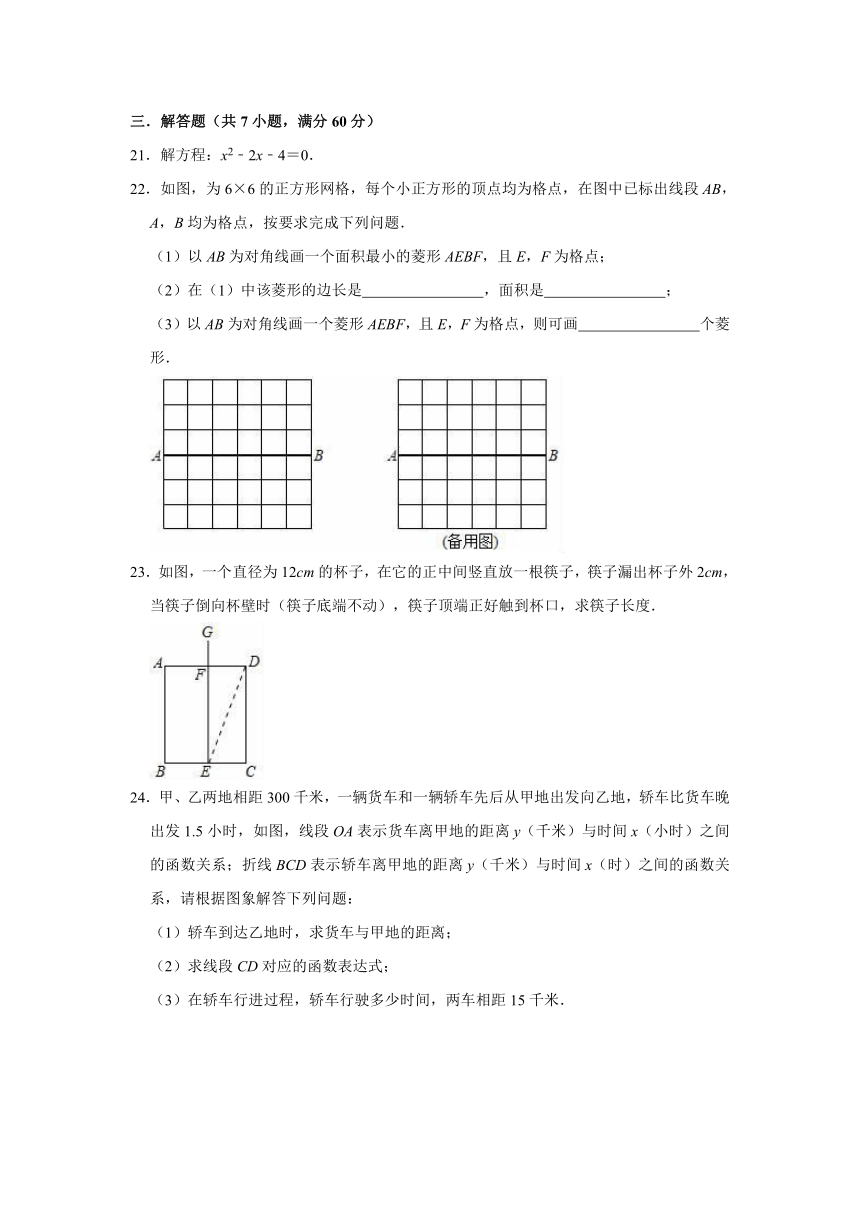
21.解方程:x2﹣2x﹣4=0.
22.如图,为6×6的正方形网格,每个小正方形的顶点均为格点,在图中已标出线段AB,A,B均为格点,按要求完成下列问题.
(1)以AB为对角线画一个面积最小的菱形AEBF,且E,F为格点;
(2)在(1)中该菱形的边长是
,面积是
;
(3)以AB为对角线画一个菱形AEBF,且E,F为格点,则可画
个菱形.
23.如图,一个直径为12cm的杯子,在它的正中间竖直放一根筷子,筷子漏出杯子外2cm,当筷子倒向杯壁时(筷子底端不动),筷子顶端正好触到杯口,求筷子长度.
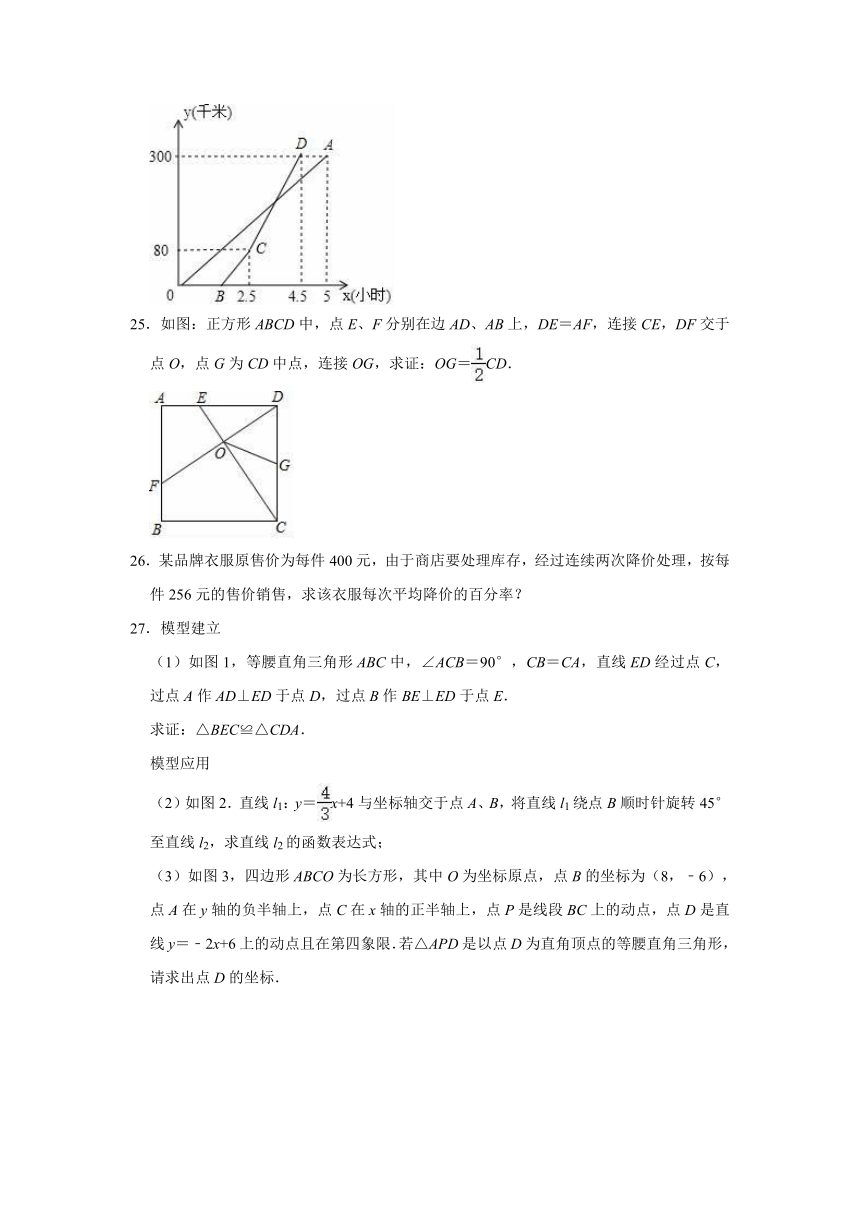
24.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
25.如图:正方形ABCD中,点E、F分别在边AD、AB上,DE=AF,连接CE,DF交于点O,点G为CD中点,连接OG,求证:OG=CD.
26.某品牌衣服原售价为每件400元,由于商店要处理库存,经过连续两次降价处理,按每件256元的售价销售,求该衣服每次平均降价的百分率?
27.模型建立
(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E.
求证:△BEC≌△CDA.
模型应用
(2)如图2.直线l1:y=x+4与坐标轴交于点A、B,将直线l1绕点B顺时针旋转45°至直线l2,求直线l2的函数表达式;
(3)如图3,四边形ABCO为长方形,其中O为坐标原点,点B的坐标为(8,﹣6),点A在y轴的负半轴上,点C在x轴的正半轴上,点P是线段BC上的动点,点D是直线y=﹣2x+6上的动点且在第四象限.若△APD是以点D为直角顶点的等腰直角三角形,请求出点D的坐标.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、当a=0时,该方程不是一元二次方程,故此选项不符合题意;
B、它是分式方程,故此选项不符合题意;
C、该方程符合一元二次方程的定义,故此选项符合题意;
D、含有两个未知数,不是一元二次方程,故此选项不符合题意.
故选:C.
2.解:A、∵42+52≠62,∴不能构成直角三角形,故A错误;
B、∵12+12=,∴能构成直角三角形,故B正确;
C、∵62+82≠112,∴不能构成直角三角形,故C错误;
D、∵52+122≠232,∴不能构成直角三角形,故D错误.
故选:B.
3.解:∵(﹣1,3)在一次函数y=kx+5的图象上,
∴3=﹣k+5,
解得:k=2,
∴函数解析式为y=2x+5,
∵点(﹣3,y1)、(2,y2)在一次函数y=2x+5的图象上,
∴y1=﹣6+5=﹣1,
y2=2×2+5=9,
∵﹣1<3<9,
∴y1<3<y2,
故选:B.
4.解:
∵四边形ABCD是平行四边形,
∴∠C=∠A,BC∥AD,
∴∠A+∠B=180°,
∵∠B=4∠A,
∴∠A=36°,
∴∠C=∠A=36°,
故选:B.
5.解:因为函数y=﹣2x+2,
所以①当x>1时,y<0,正确;②它的图象经过第二、一、四象限,错误;③它的图象必经过点(﹣2,﹣2),错误;④y的值随x的增大而减小,错误;
故选:A.
6.解:结合图象,当x>3时,y1<y2,即kx+b<x+a,
所以不等式kx﹣x<a﹣b的解集为x>3.
故选:B.
7.解:如图所示,
∵点E、F、G分别是△ABC的边AB、边BC、边CA的中点,
∴AE=BE=GF=AB,AG=CG=EF=AC,BF=CF=EG=BC,GF∥AB,EG∥BC,EF∥AC,
∴四边形AEFG、BEGF、CFEG都是平行四边形.
故选:C.
8.解:①两条平行线被第三条直线所截,内错角相等,原命题是假命题.
②三角形的内角和是180°,是真命题.
③在同一平面内,平行于同一条直线的两条直线平行,是真命题.
④相等的角不一定是对顶角,原命题是假命题.
⑤两点之间,线段最短,是真命题;
故选:B.
9.解:设道路的宽为xm,则草坪的长为(32﹣2x)m,宽为(20﹣x)m,
根据题意得:(32﹣2x)(20﹣x)=570.
故选:D.
10.解:根据题意可知火车进入隧道的时间x与火车在隧道内的长度y之间的关系具体可描述为:当火车开始进入时y逐渐变大,火车完全进入后一段时间内y不变,当火车开始出来时y逐渐变小,故反映到图象上应选B.
故选:B.
二.填空题(共10小题,满分30分,每小题3分)
11.解:根据题意得,x﹣1≥0且x﹣2≠0,
解得x≥1且x≠2.
故答案为:x≥1且x≠2.
12.解:∵x=﹣1是一元二次方程ax2+bx﹣10=0的一个解,
∴a﹣b﹣10=0,
∴a﹣b=10.
∵a≠﹣b,
∴a+b≠0,
∴====5,
故答案是:5.
13.解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,∠A=∠C,
∵∠C=∠B+∠D,
∴∠C=2∠D,∠C+∠D=180°,
∴∠A=∠C=120°,∠D=60°.
故答案为120°.
14.解:设正比例函数的解析式为y=kx(k≠0),
∵图象经过点P(a,3a),
∴3a=ak,
∴k=3,
此函数的解析式是:y=3x;
故答案为:y=3x
15.解:∵四边形ABCD是菱形,
∴∠ABO=∠CBO=30°,∠BOC=90°,
∵OC=2cm,
∴OB=2cm,
∴=cm2.
∴菱形ABCD的面积为2cm2.
故答案为:8cm2.
16.解:∵当x=0时,y=4,
当y=0时,x=﹣,
∴直线与y轴的交点分别为(0,4),与x轴的交点分别为(﹣,0),
∴×4×|﹣|=8,
解得,k=±1,
故答案为:k=±1.
17.解:∵x2﹣8x+12=0,
∴(x﹣2)(x﹣6)=0,
则x﹣2=0或x﹣6=0,
解得x=2或x=6,
当x=2时,三角形的三边为5、5、2,此时周长为12;
当x=6时,三角形三边的长为6、6、5或6、5、5,此时周长为17或16;
综上,该等腰三角形的周长为12,16或17.
故答案为:12,16或17.
18.解:如图,连接BC',
∵∠ADB=60°,∠C=45°,
∴∠CAD=∠C'AD=∠ADB﹣∠C=15°,∠CAC'=30°,
∴∠C'AB=90°﹣∠C'AC=60°,
又∵AC'=AC=AB,
∴△C'AB为等边三角形,
∴AB=BC',即AB与BC′的比值为1.
故答案为:1.
19.解:如图,过点E作EF⊥AD于点F,
在矩形ABCD中,∠B=∠BAD=90°,
∵EA是∠BAD的平分线,
∴∠DAB=∠EAF=45°,
∴∠AEB=45°,
∴AB=BE,
∴矩形ABEF是正方形,
∴AB=BE=EF=AF=4,
∴DF=AD﹣AF=6﹣4=2,
∴DE===2.
故答案为:2.
20.解:如图1,过P作PH⊥OY交于点H,
∵PD∥OY,PE∥OX,
∴四边形EODP是平行四边形,∠HEP=∠XOY=60°,
∴EP=OD=a,
Rt△HEP中,∠EPH=30°,
∴EH=EP=a,
∴a+2b=2(a+b)=2(EH+EO)=2OH,
当P在AC边上时,H与C重合,此时OH的最小值=OC=OA=1,即a+2b的最小值是2;
当P在点B时,如图2,OC=1,AC=BC=,
Rt△CHP中,∠HCP=30°,
∴PH=,CH=,
则OH的最大值是:OC+CH=1+=,即(a+2b)的最大值是5,
∴2≤a+2b≤5.
三.解答题(共7小题,满分60分)
21.解:由原方程移项,得
x2﹣2x=4,
等式两边同时加上一次项系数一半的平方,得
x2﹣2x+1=5,
配方,得
(x﹣1)2=5,
∴x=1±,
∴x1=1+,x2=1﹣.
22.解:(1)如图,菱形AEBF即为所求.
(2)AE==,菱形AEBF的面积=×6×2=6,
故答案为,6.
(3)如图备用图可知:可以画3个菱形,
故答案为3.
23.解:设杯子的高度是xcm,那么筷子的高度是(x+2)cm,
∵杯子的直径为12cm,
∴杯子半径为6cm,
∴x2+62=(x+2)2,
即x2+36=x2+4x+4,
解得:x=8,
8+2=10(cm).
答:筷子长10cm.
24.解:(1)由图象可得,
货车的速度为300÷5=60(千米/小时),
则轿车到达乙地时,货车与甲地的距离是60×4.5=270(千米),
即轿车到达乙地时,货车与甲地的距离是270千米;
(2)设线段CD对应的函数表达式是y=kx+b,
∵点C(2.5,80),点D(4.5,300),
∴,
解得,
即线段CD对应的函数表达式是y=110x﹣195(2.5≤x≤4.5);
(3)当x=2.5时,两车之间的距离为:60×2.5﹣80=70,
∵70>15,
∴在轿车行进过程,两车相距15千米时间是在2.5~4.5之间,
由图象可得,线段OA对应的函数解析式为y=60x,
则|60x﹣(110x﹣195)|=15,
解得x1=3.6,x2=4.2,
∵轿车比货车晚出发1.5小时,3.6﹣1.5=2.1(小时),4.2﹣1.5=2.7(小时),
∴在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米,
答:在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米.
25.证明:∵四边形ABCD是正方形,
∴AD=AB=CD,∠BAD=∠ADC=90°,
又∵DE=AF,
∴△ADF≌△DCE(SAS),
∴∠ADF=∠DCE,
∵∠ADF+∠CDF=90°,
∴∠DCE+∠CDF=90°,
∴∠DOC=90°,
∵点G为CD中点,
∴OG=CD.
26.解:第一次降价后的价格为:400(1﹣x),第二次降价后的价格为:400(1﹣x)2;
则可列方程:400(1﹣x)2=256,
解得x1=0.2=20%,x2=1.8(舍去).
答:该衣服每次平均降价的百分率是20%.
27.解:(1)如图1,∵△ABC为等腰直角三角形,
∴CB=CA,∠ACD+∠BCE=90°,
又∵AD⊥ED,BE⊥ED,
∴∠D=∠E=90°,∠EBC+∠BCE=90°,
∴∠ACD=∠EBC,
在△ACD与△CBE中,
,
∴△ACD≌△CBE(AAS);
(2)∵直线y=x+4与y轴交于点A,与x轴交于点B,
∴A(0,4)、B(﹣3,0),如图2,
过点B做BC⊥AB交直线l2于点C,过点C作CD⊥x轴,
在△BDC和△AOB中,
,
∴△BDC≌△AOB(AAS),
∴CD=BO=3,BD=AO=4,
∴OD=OB+BD=3+4=7,
∴C点坐标为(﹣7,3),
设l2的解析式为y=kx+b,将A,C点坐标代入,得,解得,
解得
∴l2的函数表达式为y=x+4;
(3)存在,理由:
当点D是直线y=﹣2x+6上的动点且在第四象限时,分两种情况:
当点D在矩形AOCB的内部时,如图,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,
设D(x,﹣2x+6),则OE=2x﹣6,AE=6﹣(2x﹣6)=12﹣2x,DF=EF﹣DE=8﹣x,
由(1)可得,△ADE≌△DPF,则DF=AE,
即:12﹣2x=8﹣x,
解得x=4,
∴﹣2x+6=﹣2,
∴D(4,﹣2),
此时,PF=ED=4,CP=6=CB,符合题意;
当点D在矩形AOCB的外部时,如图,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,
设D(x,﹣2x+6),则OE=2x﹣6,AE=OE﹣OA=2x﹣6﹣6=2x﹣12,DF=EF﹣DE=8﹣x,
同理可得:△ADE≌△DPF,则AE=DF,
即:2x﹣12=8﹣x,
解得x=,
∴﹣2x+6=﹣,
∴D(,﹣),
此时,ED=PF=,AE=BF=,BP=PF﹣BF=<6,符合题意,
综上,点D的坐标为(4,﹣2)或(,﹣).
一.选择题(共10小题,满分30分,每小题3分)
1.下列方程中,是一元二次方程的是( )
A.ax2+bx+c=0
B.x2+=1
C.x2﹣1=0
D.2x+3y﹣5=0
2.下列各组数中,能构成直角三角形的是( )
A.4,5,6
B.1,1,
C.6,8,11
D.5,12,23
3.已知点(﹣3,y1)、(﹣1,3)、(2,y2)在一次函数y=kx+5的图象上,则y1,y2,3的大小关系正确( )
A.3<y2<y1
B.y1<3<y2
C.y2<y1<3
D.y2<3<y1
4.已知平行四边形ABCD中,∠B=4∠A,则∠C=( )
A.18°
B.36°
C.72°
D.144°
5.对于函数y=﹣2x+2,下列结论:①当x>1时,y<0;②它的图象经过第一、二、三象限;③它的图象必经过点(﹣2,2);④y的值随x的增大而增大,其中正确结论的个数是( )
A.1
B.2
C.3
D.4
6.如图是一次函数y1=kx+b与y2=x+a的图象,则不等式kx﹣x<a﹣b的解集是( )
A.x<3
B.x>3
C.x<a+b
D.x>a﹣b
7.以三角形三边中点和三角形三个顶点能画出平行四边形有( )个
A.1
B.2
C.3
D.4
8.下列命题是真命题的个数为( )
①两条直线被第三条直线所截,内错角相等.
②三角形的内角和是180°.
③在同一平面内,平行于同一条直线的两条直线平行.
④相等的角是对顶角.
⑤两点之间,线段最短.
A.2
B.3
C.4
D.5
9.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是( )
A.32x+2×20x﹣2x2=570
B.32x+2×20x=32×20﹣570
C.(32﹣2x)(20﹣x)=32×20﹣570
D.(32﹣2x)(20﹣x)=570
10.如图,火车匀速通过隧道(隧道长大于火车长)时,火车在隧道内的长度y与火车进入隧道的时间x之间的关系用图象描述大致是( )
A.
B.
C.
D.
二.填空题(共10小题,满分30分,每小题3分)
11.函数中,自变量x的取值范围是
.
12.已知x=﹣1是一元二次方程ax2+bx﹣10=0的一个解,且a≠﹣b,则的值为
.
13.?ABCD中,∠C=∠B+∠D,则∠A=
.
14.已知正比例函数经过点P(a,3a)(其中a为常数,a≠0),则该正比例函数解析式为
.
15.如图,已知菱形ABCD的对角线AC、BD交于点O,OC=2cm,∠ABO=30°,则菱形
ABCD的面积是
.
16.已知直线y=kx+4,该直线与两坐标轴围成的三角形面积为8,那么k的值是
.
17.已知一等腰三角形的一边长为5,另一边长为方程x2﹣8x+12=0的根,该等腰三角形的周长为
.
18.如图,在等腰直角△ABC中,AB=AC,点D在边BC上,∠ADB=60°,将△ADC沿AD翻折后点C落在点C′,则AB与BC′的比值为
.
19.如图,在矩形ABCD中,AD=6,AB=4,∠BAD的平分线交BC于点E,则DE=
.
20.如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是
.
三.解答题(共7小题,满分60分)
21.解方程:x2﹣2x﹣4=0.
22.如图,为6×6的正方形网格,每个小正方形的顶点均为格点,在图中已标出线段AB,A,B均为格点,按要求完成下列问题.
(1)以AB为对角线画一个面积最小的菱形AEBF,且E,F为格点;
(2)在(1)中该菱形的边长是
,面积是
;
(3)以AB为对角线画一个菱形AEBF,且E,F为格点,则可画
个菱形.
23.如图,一个直径为12cm的杯子,在它的正中间竖直放一根筷子,筷子漏出杯子外2cm,当筷子倒向杯壁时(筷子底端不动),筷子顶端正好触到杯口,求筷子长度.
24.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
25.如图:正方形ABCD中,点E、F分别在边AD、AB上,DE=AF,连接CE,DF交于点O,点G为CD中点,连接OG,求证:OG=CD.
26.某品牌衣服原售价为每件400元,由于商店要处理库存,经过连续两次降价处理,按每件256元的售价销售,求该衣服每次平均降价的百分率?
27.模型建立
(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E.
求证:△BEC≌△CDA.
模型应用
(2)如图2.直线l1:y=x+4与坐标轴交于点A、B,将直线l1绕点B顺时针旋转45°至直线l2,求直线l2的函数表达式;
(3)如图3,四边形ABCO为长方形,其中O为坐标原点,点B的坐标为(8,﹣6),点A在y轴的负半轴上,点C在x轴的正半轴上,点P是线段BC上的动点,点D是直线y=﹣2x+6上的动点且在第四象限.若△APD是以点D为直角顶点的等腰直角三角形,请求出点D的坐标.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、当a=0时,该方程不是一元二次方程,故此选项不符合题意;
B、它是分式方程,故此选项不符合题意;
C、该方程符合一元二次方程的定义,故此选项符合题意;
D、含有两个未知数,不是一元二次方程,故此选项不符合题意.
故选:C.
2.解:A、∵42+52≠62,∴不能构成直角三角形,故A错误;
B、∵12+12=,∴能构成直角三角形,故B正确;
C、∵62+82≠112,∴不能构成直角三角形,故C错误;
D、∵52+122≠232,∴不能构成直角三角形,故D错误.
故选:B.
3.解:∵(﹣1,3)在一次函数y=kx+5的图象上,
∴3=﹣k+5,
解得:k=2,
∴函数解析式为y=2x+5,
∵点(﹣3,y1)、(2,y2)在一次函数y=2x+5的图象上,
∴y1=﹣6+5=﹣1,
y2=2×2+5=9,
∵﹣1<3<9,
∴y1<3<y2,
故选:B.
4.解:
∵四边形ABCD是平行四边形,
∴∠C=∠A,BC∥AD,
∴∠A+∠B=180°,
∵∠B=4∠A,
∴∠A=36°,
∴∠C=∠A=36°,
故选:B.
5.解:因为函数y=﹣2x+2,
所以①当x>1时,y<0,正确;②它的图象经过第二、一、四象限,错误;③它的图象必经过点(﹣2,﹣2),错误;④y的值随x的增大而减小,错误;
故选:A.
6.解:结合图象,当x>3时,y1<y2,即kx+b<x+a,
所以不等式kx﹣x<a﹣b的解集为x>3.
故选:B.
7.解:如图所示,
∵点E、F、G分别是△ABC的边AB、边BC、边CA的中点,
∴AE=BE=GF=AB,AG=CG=EF=AC,BF=CF=EG=BC,GF∥AB,EG∥BC,EF∥AC,
∴四边形AEFG、BEGF、CFEG都是平行四边形.
故选:C.
8.解:①两条平行线被第三条直线所截,内错角相等,原命题是假命题.
②三角形的内角和是180°,是真命题.
③在同一平面内,平行于同一条直线的两条直线平行,是真命题.
④相等的角不一定是对顶角,原命题是假命题.
⑤两点之间,线段最短,是真命题;
故选:B.
9.解:设道路的宽为xm,则草坪的长为(32﹣2x)m,宽为(20﹣x)m,
根据题意得:(32﹣2x)(20﹣x)=570.
故选:D.
10.解:根据题意可知火车进入隧道的时间x与火车在隧道内的长度y之间的关系具体可描述为:当火车开始进入时y逐渐变大,火车完全进入后一段时间内y不变,当火车开始出来时y逐渐变小,故反映到图象上应选B.
故选:B.
二.填空题(共10小题,满分30分,每小题3分)
11.解:根据题意得,x﹣1≥0且x﹣2≠0,
解得x≥1且x≠2.
故答案为:x≥1且x≠2.
12.解:∵x=﹣1是一元二次方程ax2+bx﹣10=0的一个解,
∴a﹣b﹣10=0,
∴a﹣b=10.
∵a≠﹣b,
∴a+b≠0,
∴====5,
故答案是:5.
13.解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,∠A=∠C,
∵∠C=∠B+∠D,
∴∠C=2∠D,∠C+∠D=180°,
∴∠A=∠C=120°,∠D=60°.
故答案为120°.
14.解:设正比例函数的解析式为y=kx(k≠0),
∵图象经过点P(a,3a),
∴3a=ak,
∴k=3,
此函数的解析式是:y=3x;
故答案为:y=3x
15.解:∵四边形ABCD是菱形,
∴∠ABO=∠CBO=30°,∠BOC=90°,
∵OC=2cm,
∴OB=2cm,
∴=cm2.
∴菱形ABCD的面积为2cm2.
故答案为:8cm2.
16.解:∵当x=0时,y=4,
当y=0时,x=﹣,
∴直线与y轴的交点分别为(0,4),与x轴的交点分别为(﹣,0),
∴×4×|﹣|=8,
解得,k=±1,
故答案为:k=±1.
17.解:∵x2﹣8x+12=0,
∴(x﹣2)(x﹣6)=0,
则x﹣2=0或x﹣6=0,
解得x=2或x=6,
当x=2时,三角形的三边为5、5、2,此时周长为12;
当x=6时,三角形三边的长为6、6、5或6、5、5,此时周长为17或16;
综上,该等腰三角形的周长为12,16或17.
故答案为:12,16或17.
18.解:如图,连接BC',
∵∠ADB=60°,∠C=45°,
∴∠CAD=∠C'AD=∠ADB﹣∠C=15°,∠CAC'=30°,
∴∠C'AB=90°﹣∠C'AC=60°,
又∵AC'=AC=AB,
∴△C'AB为等边三角形,
∴AB=BC',即AB与BC′的比值为1.
故答案为:1.
19.解:如图,过点E作EF⊥AD于点F,
在矩形ABCD中,∠B=∠BAD=90°,
∵EA是∠BAD的平分线,
∴∠DAB=∠EAF=45°,
∴∠AEB=45°,
∴AB=BE,
∴矩形ABEF是正方形,
∴AB=BE=EF=AF=4,
∴DF=AD﹣AF=6﹣4=2,
∴DE===2.
故答案为:2.
20.解:如图1,过P作PH⊥OY交于点H,
∵PD∥OY,PE∥OX,
∴四边形EODP是平行四边形,∠HEP=∠XOY=60°,
∴EP=OD=a,
Rt△HEP中,∠EPH=30°,
∴EH=EP=a,
∴a+2b=2(a+b)=2(EH+EO)=2OH,
当P在AC边上时,H与C重合,此时OH的最小值=OC=OA=1,即a+2b的最小值是2;
当P在点B时,如图2,OC=1,AC=BC=,
Rt△CHP中,∠HCP=30°,
∴PH=,CH=,
则OH的最大值是:OC+CH=1+=,即(a+2b)的最大值是5,
∴2≤a+2b≤5.
三.解答题(共7小题,满分60分)
21.解:由原方程移项,得
x2﹣2x=4,
等式两边同时加上一次项系数一半的平方,得
x2﹣2x+1=5,
配方,得
(x﹣1)2=5,
∴x=1±,
∴x1=1+,x2=1﹣.
22.解:(1)如图,菱形AEBF即为所求.
(2)AE==,菱形AEBF的面积=×6×2=6,
故答案为,6.
(3)如图备用图可知:可以画3个菱形,
故答案为3.
23.解:设杯子的高度是xcm,那么筷子的高度是(x+2)cm,
∵杯子的直径为12cm,
∴杯子半径为6cm,
∴x2+62=(x+2)2,
即x2+36=x2+4x+4,
解得:x=8,
8+2=10(cm).
答:筷子长10cm.
24.解:(1)由图象可得,
货车的速度为300÷5=60(千米/小时),
则轿车到达乙地时,货车与甲地的距离是60×4.5=270(千米),
即轿车到达乙地时,货车与甲地的距离是270千米;
(2)设线段CD对应的函数表达式是y=kx+b,
∵点C(2.5,80),点D(4.5,300),
∴,
解得,
即线段CD对应的函数表达式是y=110x﹣195(2.5≤x≤4.5);
(3)当x=2.5时,两车之间的距离为:60×2.5﹣80=70,
∵70>15,
∴在轿车行进过程,两车相距15千米时间是在2.5~4.5之间,
由图象可得,线段OA对应的函数解析式为y=60x,
则|60x﹣(110x﹣195)|=15,
解得x1=3.6,x2=4.2,
∵轿车比货车晚出发1.5小时,3.6﹣1.5=2.1(小时),4.2﹣1.5=2.7(小时),
∴在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米,
答:在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米.
25.证明:∵四边形ABCD是正方形,
∴AD=AB=CD,∠BAD=∠ADC=90°,
又∵DE=AF,
∴△ADF≌△DCE(SAS),
∴∠ADF=∠DCE,
∵∠ADF+∠CDF=90°,
∴∠DCE+∠CDF=90°,
∴∠DOC=90°,
∵点G为CD中点,
∴OG=CD.
26.解:第一次降价后的价格为:400(1﹣x),第二次降价后的价格为:400(1﹣x)2;
则可列方程:400(1﹣x)2=256,
解得x1=0.2=20%,x2=1.8(舍去).
答:该衣服每次平均降价的百分率是20%.
27.解:(1)如图1,∵△ABC为等腰直角三角形,
∴CB=CA,∠ACD+∠BCE=90°,
又∵AD⊥ED,BE⊥ED,
∴∠D=∠E=90°,∠EBC+∠BCE=90°,
∴∠ACD=∠EBC,
在△ACD与△CBE中,
,
∴△ACD≌△CBE(AAS);
(2)∵直线y=x+4与y轴交于点A,与x轴交于点B,
∴A(0,4)、B(﹣3,0),如图2,
过点B做BC⊥AB交直线l2于点C,过点C作CD⊥x轴,
在△BDC和△AOB中,
,
∴△BDC≌△AOB(AAS),
∴CD=BO=3,BD=AO=4,
∴OD=OB+BD=3+4=7,
∴C点坐标为(﹣7,3),
设l2的解析式为y=kx+b,将A,C点坐标代入,得,解得,
解得
∴l2的函数表达式为y=x+4;
(3)存在,理由:
当点D是直线y=﹣2x+6上的动点且在第四象限时,分两种情况:
当点D在矩形AOCB的内部时,如图,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,
设D(x,﹣2x+6),则OE=2x﹣6,AE=6﹣(2x﹣6)=12﹣2x,DF=EF﹣DE=8﹣x,
由(1)可得,△ADE≌△DPF,则DF=AE,
即:12﹣2x=8﹣x,
解得x=4,
∴﹣2x+6=﹣2,
∴D(4,﹣2),
此时,PF=ED=4,CP=6=CB,符合题意;
当点D在矩形AOCB的外部时,如图,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,
设D(x,﹣2x+6),则OE=2x﹣6,AE=OE﹣OA=2x﹣6﹣6=2x﹣12,DF=EF﹣DE=8﹣x,
同理可得:△ADE≌△DPF,则AE=DF,
即:2x﹣12=8﹣x,
解得x=,
∴﹣2x+6=﹣,
∴D(,﹣),
此时,ED=PF=,AE=BF=,BP=PF﹣BF=<6,符合题意,
综上,点D的坐标为(4,﹣2)或(,﹣).
同课章节目录
