2020-2021学年人教五四版七年级下册数学期末练习试题(word版含解析)
文档属性
| 名称 | 2020-2021学年人教五四版七年级下册数学期末练习试题(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 248.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-22 00:00:00 | ||
图片预览



文档简介
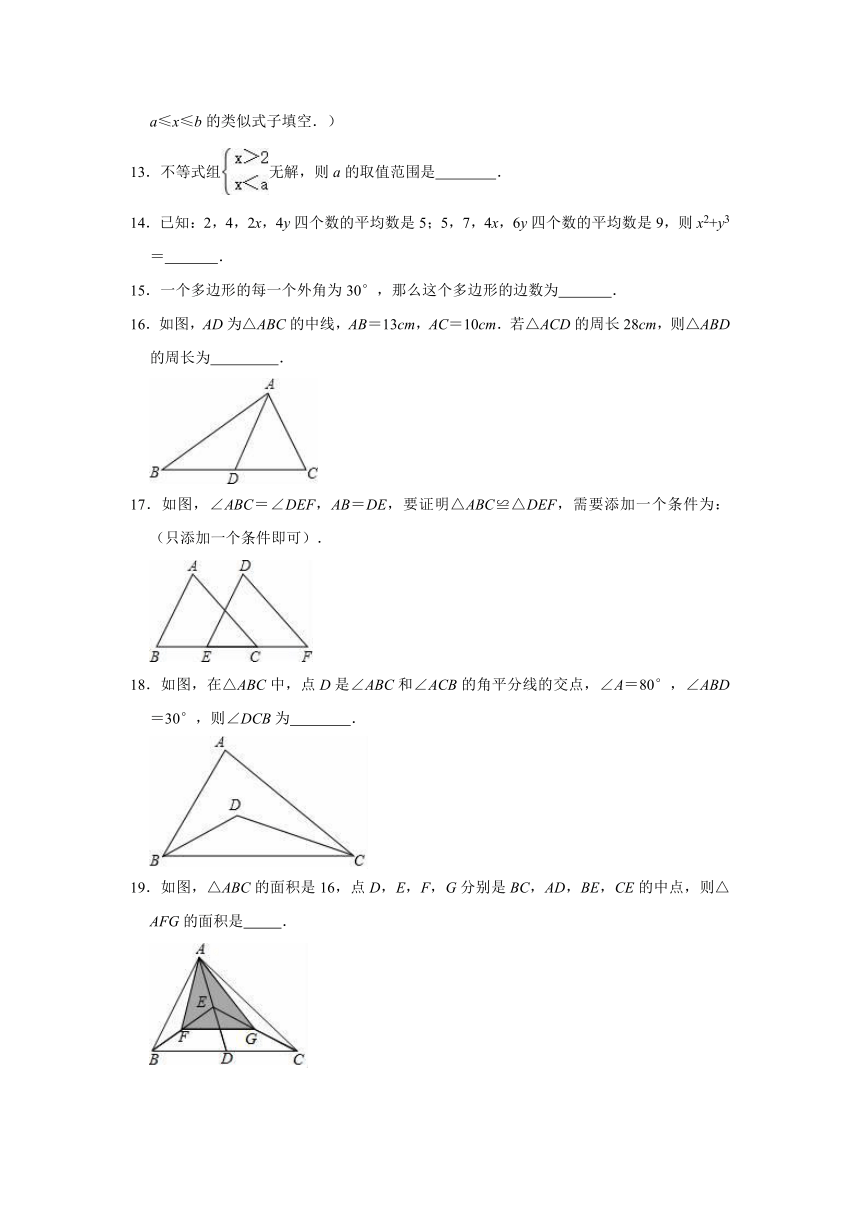
2020-2021学年人教五四版七年级下册数学期末练习试题
一.选择题(共10小题,满分30分,每小题3分)
1.下列x的值不是不等式﹣2x+4<0的解,答案是( )
A.﹣2
B.3
C.3.5
D.10
2.小华在某月的日历中圈出几个数,算得这三个数的和为36,那么这几个数的形式可能是( )
A.
B.
C.
D.
3.如图是根据某班40名同学一周的体育锻炼情况绘制的统计图,该班40名同学一周参加体育锻炼时间的中位数,众数分别是( )
A.10.5,16
B.8.5,16
C.8.5,8
D.9,8
4.如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( )
A.AB=DC
B.OB=OC
C.∠C=∠D
D.∠AOB=∠DOC
5.关于x的不等式组只有3个整数解,则a的取值范围是( )
A.﹣3≤a≤﹣2
B.﹣3≤a<﹣2
C.﹣3<a≤﹣2
D.﹣3<a<﹣2
6.如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
7.不等式组的解集为( )
A.x≥﹣2
B.﹣2<x<3
C.x>3
D.﹣2≤x<3
8.为备战2008年北京奥运会,甲、乙两名运动员训练测验,两名运动员的平均分相同,且S2甲=0.01,S2乙=0.006,则成绩较稳定的是( )运动员.
A.甲
B.乙
C.两运动员一样稳定
D.无法确定
9.下列说法正确的是 )
A.两条不相交的直线一定平行
B.三角形三条高线交于一点
C.过一点有且只有一条直线与已知直线垂直
D.直线外一点到这条直线的垂线段的长度叫做这个点到直线的距离
10.《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺,问木长多少尺.设木长为x尺,绳子长为y尺,则下列符合题意的方程组是( )
A.
B.
C.
D.
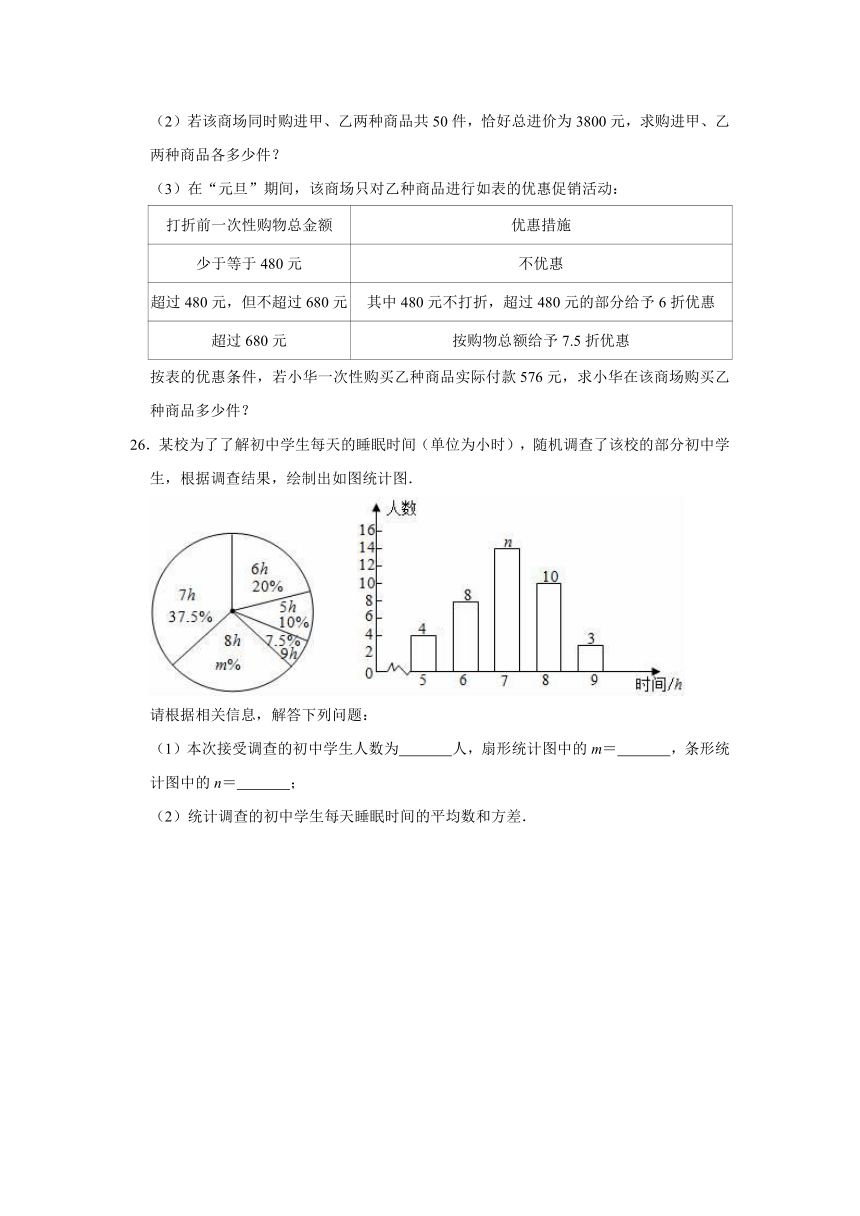
二.填空题(共10小题,满分30分,每小题3分)
11.已知2ax+yb3与﹣a2bx﹣y是同类项,则(x+y)(x﹣y)=
.
12.k的值大于﹣1且不大于3,则用不等式表示
k的取值范围是
.(使用形如a≤x≤b的类似式子填空.)
13.不等式组无解,则a的取值范围是
.
14.已知:2,4,2x,4y四个数的平均数是5;5,7,4x,6y四个数的平均数是9,则x2+y3=
.
15.一个多边形的每一个外角为30°,那么这个多边形的边数为
.
16.如图,AD为△ABC的中线,AB=13cm,AC=10cm.若△ACD的周长28cm,则△ABD的周长为
.
17.如图,∠ABC=∠DEF,AB=DE,要证明△ABC≌△DEF,需要添加一个条件为:
(只添加一个条件即可).
18.如图,在△ABC中,点D是∠ABC和∠ACB的角平分线的交点,∠A=80°,∠ABD=30°,则∠DCB为
.
19.如图,△ABC的面积是16,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是
.
20.请写一个二元一次方程组
,使它的解是.
三.解答题(共6小题,满分38分)
21.解方程组
(1);
(2);
22.解下列不等式(组),并把它们的解集分别表示在数轴上;
(1)解不等式:﹣<4;
(2)解不等式组:.
23.如图,点B,C,E,F在同一直线上,点A,D在BC的异侧,AB=CD,BF=CE,∠B=∠C.
(1)求证:AE∥DF.
(2)若∠A+∠D=144°,∠C=30°,求∠AEC的度数.
24.某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A,B两种园艺造型共50个,摆放在迎宾大道两侧,已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆.
(1)某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明哪种方案成本最低,最低成本是多少元?
25.平价商场经销的甲,乙两种商品,甲种商品每件售价98元,利润率为40%;乙种商品每件进价80元,售价128元.
(1)求甲种商品每件的进价;(利润率=×100%)
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为3800元,求购进甲、乙两种商品各多少件?
(3)在“元旦”期间,该商场只对乙种商品进行如表的优惠促销活动:
打折前一次性购物总金额
优惠措施
少于等于480元
不优惠
超过480元,但不超过680元
其中480元不打折,超过480元的部分给予6折优惠
超过680元
按购物总额给予7.5折优惠
按表的优惠条件,若小华一次性购买乙种商品实际付款576元,求小华在该商场购买乙种商品多少件?
26.某校为了了解初中学生每天的睡眠时间(单位为小时),随机调查了该校的部分初中学生,根据调查结果,绘制出如图统计图.
请根据相关信息,解答下列问题:
(1)本次接受调查的初中学生人数为
人,扇形统计图中的m=
,条形统计图中的n=
;
(2)统计调查的初中学生每天睡眠时间的平均数和方差.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:不等式﹣2x+4<0,
解得:x>2,
则﹣2不是不等式的解.
故选:A.
2.解:第一个图中:设下面的数是x,则上面的数是x﹣7,右边的是x﹣6.根据题意得:x+(x﹣7)+(x﹣6)=36,解得x=不合题意.
第二图中:设下面的数是x,则上面的数是x﹣7,左边的数是x﹣8.根据题意得:x+(x﹣7)+(x﹣8)=36,解得x=17,符合题意.可能是这种形式.
第三图中:设下面左边的数是x,则右边的数是:x+2,上面的数是x+1﹣7=x﹣6,根据题意得:x+(x+2)+(x﹣6)=36解得:x=,不合题意.
第四图中:设下面左边的数是x,则上边左边的是:x﹣7﹣1=x﹣8右边的数是:x﹣7+1=x﹣6根据题意得:x+(x﹣8)+(x﹣6)=36解得:x=,不合题意.
故选:B.
3.解:将这组数据从小到大的顺序排列后,处于中间位置的那个数,由中位数的定义可知,这组数据的中位数是9;
众数是一组数据中出现次数最多的数,即8;
故选:D.
4.解:A、AB=DC,不能根据SAS证两三角形全等,故本选项错误;
B、∵在△AOB和△DOC中
,
∴△AOB≌△DOC(SAS),故本选项正确;
C、两三角形相等的条件只有OA=OD和∠AOB=∠DOC,不能证两三角形全等,故本选项错误;
D、根据∠AOB=∠DOC和OA=OD,不能证两三角形全等,故本选项错误;
故选:B.
5.解:,
由①得:x>a,
由②得:x<1,
∴不等式组的解集为:a<x<1,
∵只有3个整数解,
∴整数解为:0,﹣1,﹣2,
∴﹣3≤a<﹣2,
故选:B.
6.解:需要添加的条件为BC=BD或AC=AD,理由为:
若添加的条件为BC=BD,
在Rt△ABC与Rt△ABD中,
∵,
∴Rt△ABC≌Rt△ABD(HL);
若添加的条件为AC=AD,
在Rt△ABC与Rt△ABD中,
∵,
∴Rt△ABC≌Rt△ABD(HL).
故选:A.
7.解:,
解①得:x>3,
解②得:x≥﹣2,
所以不等式组的解集为:x>3.
故选:C.
8.解:由于S甲2>S乙2,则成绩较稳定的同学是乙.
故选:B.
9.解:A、在同一平面内,两条不相交的直线一定平行,故不符合题意;
B、三角形的三条高线所在的直线交于一点,故不符合题意;
C、在同一平面内,过一点有且只有一条直线与已知直线垂直,故不符合题意;
D、直线外一点到这条直线的垂线段的长度叫做这个点到直线的距离,故符合题意;
故选:D.
10.解:由题意可得,
,
故选:B.
二.填空题(共10小题,满分30分,每小题3分)
11.解:∵2ax+yb3与﹣a2bx﹣y是同类项,
∴
则(x+y)(x﹣y)=2×3=6.
故答案为6.
12.解:根据题意,得﹣1<k≤3.
故填﹣1<k≤3.
13.解:∵不等式组无解,
∴a的取值范围是a≤2;
故答案为a≤2.
14.解:由题意知,(2+4+2x+4y)÷4=5,
(5+7+4x+6y)÷4=9;
∴2x+4y=14和4x+6y=24;
解这两个方程组成的方程组得,x=3,y=2;
∴x2+y3=9+8=17.
故填17.﹣
15.解:多边形的边数:360°÷30°=12,
则这个多边形的边数为12.
故答案为:12.
16.解:∵AD为△ABC的中线,
∴BD=DC,
∵△ACD的周长28cm,
∴AC+AD+CD=28(cm),
∵AC=10cm,
∴AD+CD=18(cm),即AD+BD=18(cm),
∴△ABD的周长=AB+AD+BD=31(cm),
故答案为:31cm.
17.解:所添条件为:BC=EF.
∵BC=EF,∠ABC=∠DEF,AB=DE
∴△ABC≌△DEF(SAS).
18.解:∵BD平分∠ABC,
∴∠ABC=2∠ABD=60°.
在△ABC中,∠ACB=180°﹣∠A﹣∠ABC=180°﹣80°﹣60°=40°.
又∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°.
故答案为:20°.
19.解:∵点D是BC的中点,
∴AD是△ABC的中线,
∴△ABD的面积=△ADC的面积=×△ABC的面积,
同理得:△AEF的面积=×△ABE的面积=×△ABD的面积=×△ABC的面积==2,
△AEG的面积=2,
△BCE的面积=×△ABC的面积=8,
又∵FG是△BCE的中位线,
∴△EFG的面积=×△BCE的面积==2,
∴△AFG的面积是2×3=6,
故答案为:6.
20.解:二元一次方程组,使它的解是.
故答案为:
三.解答题(共6小题,满分38分)
21.解:(1),
①×2+②得:﹣9y=﹣9,
解得:y=1,
把y=1代入②得:x=1,
则方程组的解为;
(2)方程组整理得:,
①×2+②得:11x=22,
解得:x=2,
把x=2代入①得:y=3,
则方程组的解为.
22.解:(1)原不等式变化为﹣(2x﹣2)<12,
∴2x﹣2>﹣12,
∴x>﹣5,
在数轴上表示为:
;
(2)原不等式组转化为,
化简为,
∴不等式组的解集为:﹣1<x≤5.
在数轴上表示为:
.
23.(1)证明:∵BF=CE,
∴BF+EF=CE+EF,
即BE=CF,
在△ABE和△DF中,
,
∴△ABE≌△DCF(SAS),
∴∠AEB=∠DFC,
∴AE∥DF;
(2)解:∵△ABE≌△DCF,
∴∠A=∠D,∠B=∠C=30°,
∵∠A+∠D=144°,
∴∠A=72°,
∴∠AEC=∠A+∠B=72°+30°=102°.
24.解:(1)设搭配A种造型x个,则B种造型为(50﹣x)个,
依题意得,
解这个不等式组得:31≤x≤33,
∵x是整数,
∴x可取31,32,33,
∴可设计三种搭配方案:
①A种园艺造型31个,B种园艺造型19个;
②A种园艺造型32个,B种园艺造型18个;
③A种园艺造型33个,B种园艺造型17个.
(2)设总成本为W元,
则W=200x+360x(50﹣x)=﹣160x+18000,
∵k=﹣160<0,
∴W随x的增大而减小,
则当x=33时,总成本W取得最小值,最小值为12720元.
25.解:(1)设甲种商品的进价为a元,则
98﹣a=40%a.
解得a=70.
答:甲种商品的进价为70元;
(2)设该商场购进甲种商品x件,根据题意可得:
70x+80(50﹣x)=3800,
解得:x=20;
乙种商品:50﹣20=30(件).
答:该商场购进甲种商品20件,乙种商品30件.
(3)设小华在该商场购买乙种商品b件,
根据题意,得
①当过480元,但不超过680元时,480+(128b﹣480)×0.6=576,
解得b=5.
②当超过680元时,128b×0.75=576,
解得b=6.
答:小华在该商场购买乙种商品5或6件.
26.解:(1)本次接受调查的初中学生有:4÷10%=40(人),
m%=10÷40×100%=25%,即m=25,
n=40×37.5%=15,
故答案为:40,25,15;
(2)由条形统计图可得,
=×(5×4+6×8+7×15+8×10+9×3)=7,
s2=
[(5﹣7)2×4+(6﹣7)2×8+(7﹣7)2×15+(8﹣7)2×10+(9﹣7)2×3]=1.15,
一.选择题(共10小题,满分30分,每小题3分)
1.下列x的值不是不等式﹣2x+4<0的解,答案是( )
A.﹣2
B.3
C.3.5
D.10
2.小华在某月的日历中圈出几个数,算得这三个数的和为36,那么这几个数的形式可能是( )
A.
B.
C.
D.
3.如图是根据某班40名同学一周的体育锻炼情况绘制的统计图,该班40名同学一周参加体育锻炼时间的中位数,众数分别是( )
A.10.5,16
B.8.5,16
C.8.5,8
D.9,8
4.如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( )
A.AB=DC
B.OB=OC
C.∠C=∠D
D.∠AOB=∠DOC
5.关于x的不等式组只有3个整数解,则a的取值范围是( )
A.﹣3≤a≤﹣2
B.﹣3≤a<﹣2
C.﹣3<a≤﹣2
D.﹣3<a<﹣2
6.如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
7.不等式组的解集为( )
A.x≥﹣2
B.﹣2<x<3
C.x>3
D.﹣2≤x<3
8.为备战2008年北京奥运会,甲、乙两名运动员训练测验,两名运动员的平均分相同,且S2甲=0.01,S2乙=0.006,则成绩较稳定的是( )运动员.
A.甲
B.乙
C.两运动员一样稳定
D.无法确定
9.下列说法正确的是 )
A.两条不相交的直线一定平行
B.三角形三条高线交于一点
C.过一点有且只有一条直线与已知直线垂直
D.直线外一点到这条直线的垂线段的长度叫做这个点到直线的距离
10.《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺,问木长多少尺.设木长为x尺,绳子长为y尺,则下列符合题意的方程组是( )
A.
B.
C.
D.
二.填空题(共10小题,满分30分,每小题3分)
11.已知2ax+yb3与﹣a2bx﹣y是同类项,则(x+y)(x﹣y)=
.
12.k的值大于﹣1且不大于3,则用不等式表示
k的取值范围是
.(使用形如a≤x≤b的类似式子填空.)
13.不等式组无解,则a的取值范围是
.
14.已知:2,4,2x,4y四个数的平均数是5;5,7,4x,6y四个数的平均数是9,则x2+y3=
.
15.一个多边形的每一个外角为30°,那么这个多边形的边数为
.
16.如图,AD为△ABC的中线,AB=13cm,AC=10cm.若△ACD的周长28cm,则△ABD的周长为
.
17.如图,∠ABC=∠DEF,AB=DE,要证明△ABC≌△DEF,需要添加一个条件为:
(只添加一个条件即可).
18.如图,在△ABC中,点D是∠ABC和∠ACB的角平分线的交点,∠A=80°,∠ABD=30°,则∠DCB为
.
19.如图,△ABC的面积是16,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是
.
20.请写一个二元一次方程组
,使它的解是.
三.解答题(共6小题,满分38分)
21.解方程组
(1);
(2);
22.解下列不等式(组),并把它们的解集分别表示在数轴上;
(1)解不等式:﹣<4;
(2)解不等式组:.
23.如图,点B,C,E,F在同一直线上,点A,D在BC的异侧,AB=CD,BF=CE,∠B=∠C.
(1)求证:AE∥DF.
(2)若∠A+∠D=144°,∠C=30°,求∠AEC的度数.
24.某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A,B两种园艺造型共50个,摆放在迎宾大道两侧,已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆.
(1)某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明哪种方案成本最低,最低成本是多少元?
25.平价商场经销的甲,乙两种商品,甲种商品每件售价98元,利润率为40%;乙种商品每件进价80元,售价128元.
(1)求甲种商品每件的进价;(利润率=×100%)
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为3800元,求购进甲、乙两种商品各多少件?
(3)在“元旦”期间,该商场只对乙种商品进行如表的优惠促销活动:
打折前一次性购物总金额
优惠措施
少于等于480元
不优惠
超过480元,但不超过680元
其中480元不打折,超过480元的部分给予6折优惠
超过680元
按购物总额给予7.5折优惠
按表的优惠条件,若小华一次性购买乙种商品实际付款576元,求小华在该商场购买乙种商品多少件?
26.某校为了了解初中学生每天的睡眠时间(单位为小时),随机调查了该校的部分初中学生,根据调查结果,绘制出如图统计图.
请根据相关信息,解答下列问题:
(1)本次接受调查的初中学生人数为
人,扇形统计图中的m=
,条形统计图中的n=
;
(2)统计调查的初中学生每天睡眠时间的平均数和方差.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:不等式﹣2x+4<0,
解得:x>2,
则﹣2不是不等式的解.
故选:A.
2.解:第一个图中:设下面的数是x,则上面的数是x﹣7,右边的是x﹣6.根据题意得:x+(x﹣7)+(x﹣6)=36,解得x=不合题意.
第二图中:设下面的数是x,则上面的数是x﹣7,左边的数是x﹣8.根据题意得:x+(x﹣7)+(x﹣8)=36,解得x=17,符合题意.可能是这种形式.
第三图中:设下面左边的数是x,则右边的数是:x+2,上面的数是x+1﹣7=x﹣6,根据题意得:x+(x+2)+(x﹣6)=36解得:x=,不合题意.
第四图中:设下面左边的数是x,则上边左边的是:x﹣7﹣1=x﹣8右边的数是:x﹣7+1=x﹣6根据题意得:x+(x﹣8)+(x﹣6)=36解得:x=,不合题意.
故选:B.
3.解:将这组数据从小到大的顺序排列后,处于中间位置的那个数,由中位数的定义可知,这组数据的中位数是9;
众数是一组数据中出现次数最多的数,即8;
故选:D.
4.解:A、AB=DC,不能根据SAS证两三角形全等,故本选项错误;
B、∵在△AOB和△DOC中
,
∴△AOB≌△DOC(SAS),故本选项正确;
C、两三角形相等的条件只有OA=OD和∠AOB=∠DOC,不能证两三角形全等,故本选项错误;
D、根据∠AOB=∠DOC和OA=OD,不能证两三角形全等,故本选项错误;
故选:B.
5.解:,
由①得:x>a,
由②得:x<1,
∴不等式组的解集为:a<x<1,
∵只有3个整数解,
∴整数解为:0,﹣1,﹣2,
∴﹣3≤a<﹣2,
故选:B.
6.解:需要添加的条件为BC=BD或AC=AD,理由为:
若添加的条件为BC=BD,
在Rt△ABC与Rt△ABD中,
∵,
∴Rt△ABC≌Rt△ABD(HL);
若添加的条件为AC=AD,
在Rt△ABC与Rt△ABD中,
∵,
∴Rt△ABC≌Rt△ABD(HL).
故选:A.
7.解:,
解①得:x>3,
解②得:x≥﹣2,
所以不等式组的解集为:x>3.
故选:C.
8.解:由于S甲2>S乙2,则成绩较稳定的同学是乙.
故选:B.
9.解:A、在同一平面内,两条不相交的直线一定平行,故不符合题意;
B、三角形的三条高线所在的直线交于一点,故不符合题意;
C、在同一平面内,过一点有且只有一条直线与已知直线垂直,故不符合题意;
D、直线外一点到这条直线的垂线段的长度叫做这个点到直线的距离,故符合题意;
故选:D.
10.解:由题意可得,
,
故选:B.
二.填空题(共10小题,满分30分,每小题3分)
11.解:∵2ax+yb3与﹣a2bx﹣y是同类项,
∴
则(x+y)(x﹣y)=2×3=6.
故答案为6.
12.解:根据题意,得﹣1<k≤3.
故填﹣1<k≤3.
13.解:∵不等式组无解,
∴a的取值范围是a≤2;
故答案为a≤2.
14.解:由题意知,(2+4+2x+4y)÷4=5,
(5+7+4x+6y)÷4=9;
∴2x+4y=14和4x+6y=24;
解这两个方程组成的方程组得,x=3,y=2;
∴x2+y3=9+8=17.
故填17.﹣
15.解:多边形的边数:360°÷30°=12,
则这个多边形的边数为12.
故答案为:12.
16.解:∵AD为△ABC的中线,
∴BD=DC,
∵△ACD的周长28cm,
∴AC+AD+CD=28(cm),
∵AC=10cm,
∴AD+CD=18(cm),即AD+BD=18(cm),
∴△ABD的周长=AB+AD+BD=31(cm),
故答案为:31cm.
17.解:所添条件为:BC=EF.
∵BC=EF,∠ABC=∠DEF,AB=DE
∴△ABC≌△DEF(SAS).
18.解:∵BD平分∠ABC,
∴∠ABC=2∠ABD=60°.
在△ABC中,∠ACB=180°﹣∠A﹣∠ABC=180°﹣80°﹣60°=40°.
又∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°.
故答案为:20°.
19.解:∵点D是BC的中点,
∴AD是△ABC的中线,
∴△ABD的面积=△ADC的面积=×△ABC的面积,
同理得:△AEF的面积=×△ABE的面积=×△ABD的面积=×△ABC的面积==2,
△AEG的面积=2,
△BCE的面积=×△ABC的面积=8,
又∵FG是△BCE的中位线,
∴△EFG的面积=×△BCE的面积==2,
∴△AFG的面积是2×3=6,
故答案为:6.
20.解:二元一次方程组,使它的解是.
故答案为:
三.解答题(共6小题,满分38分)
21.解:(1),
①×2+②得:﹣9y=﹣9,
解得:y=1,
把y=1代入②得:x=1,
则方程组的解为;
(2)方程组整理得:,
①×2+②得:11x=22,
解得:x=2,
把x=2代入①得:y=3,
则方程组的解为.
22.解:(1)原不等式变化为﹣(2x﹣2)<12,
∴2x﹣2>﹣12,
∴x>﹣5,
在数轴上表示为:
;
(2)原不等式组转化为,
化简为,
∴不等式组的解集为:﹣1<x≤5.
在数轴上表示为:
.
23.(1)证明:∵BF=CE,
∴BF+EF=CE+EF,
即BE=CF,
在△ABE和△DF中,
,
∴△ABE≌△DCF(SAS),
∴∠AEB=∠DFC,
∴AE∥DF;
(2)解:∵△ABE≌△DCF,
∴∠A=∠D,∠B=∠C=30°,
∵∠A+∠D=144°,
∴∠A=72°,
∴∠AEC=∠A+∠B=72°+30°=102°.
24.解:(1)设搭配A种造型x个,则B种造型为(50﹣x)个,
依题意得,
解这个不等式组得:31≤x≤33,
∵x是整数,
∴x可取31,32,33,
∴可设计三种搭配方案:
①A种园艺造型31个,B种园艺造型19个;
②A种园艺造型32个,B种园艺造型18个;
③A种园艺造型33个,B种园艺造型17个.
(2)设总成本为W元,
则W=200x+360x(50﹣x)=﹣160x+18000,
∵k=﹣160<0,
∴W随x的增大而减小,
则当x=33时,总成本W取得最小值,最小值为12720元.
25.解:(1)设甲种商品的进价为a元,则
98﹣a=40%a.
解得a=70.
答:甲种商品的进价为70元;
(2)设该商场购进甲种商品x件,根据题意可得:
70x+80(50﹣x)=3800,
解得:x=20;
乙种商品:50﹣20=30(件).
答:该商场购进甲种商品20件,乙种商品30件.
(3)设小华在该商场购买乙种商品b件,
根据题意,得
①当过480元,但不超过680元时,480+(128b﹣480)×0.6=576,
解得b=5.
②当超过680元时,128b×0.75=576,
解得b=6.
答:小华在该商场购买乙种商品5或6件.
26.解:(1)本次接受调查的初中学生有:4÷10%=40(人),
m%=10÷40×100%=25%,即m=25,
n=40×37.5%=15,
故答案为:40,25,15;
(2)由条形统计图可得,
=×(5×4+6×8+7×15+8×10+9×3)=7,
s2=
[(5﹣7)2×4+(6﹣7)2×8+(7﹣7)2×15+(8﹣7)2×10+(9﹣7)2×3]=1.15,
同课章节目录
