高中数学复习 活跃在高考中的一个恒等式-极化恒等式
文档属性
| 名称 | 高中数学复习 活跃在高考中的一个恒等式-极化恒等式 |  | |
| 格式 | |||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-22 21:35:43 | ||
图片预览



文档简介
活 跃 在 高 考 中 的 一 个 恒 等 式 — — 极 化 恒 等 式
0 1 何 谓 极 化 恒 等 式
三 角 形 模 型 :
在 中 , D 为 B C 的 中 点 :
平 行 四 边 形 模 型
在 平 行 四 边 形 A B C D 中 :
0 2 极 化 恒 等 式 应 用
例 1 , ( 2 0 1 7 全 国 I I , 理 1 2 ) 已 知 是 边 长 为 2 的 等 边 三 角 形 , P 为 平 面 内 一 点 ,
则 的 最 小 值 是 ( )
A . B . C . D .
解 法 1 ( 坐 标 法 ) :
以 B C 所 在 直 线 为 轴 , B C 的 中 垂 线 轴 建 立 平 面 直 角 坐 标 系 , ,
设 , 则 ,
,
当 且 仅 当 , 即 , 取 得 最 小 值 .
解 法 2 ( 极 化 恒 等 式 ) :
设 B C 的 重 点 为 O , O C 的 中 点 为 M , 连 接 O P , P M ,
,
当 且 仅 当 M 与 P 重 合 始 去 等 号 .
例 2 在 中 , 已 知 是 的 中 点 , E , F 分 别 是 B C , A C 上 的
动 点 , 且 E F = 1 , 则 的 最 小 值 为 ( )
A . B . C . D .
解 法 1 ( 坐 标 法 )
以 A C 所 在 直 线 为 轴 , B C 所 在 直 线 为 轴 建 立 平 面 直 角 坐 标 系 , 则
设 则 , ,
,
由 柯 西 不 等 式 可 得 : , 即 , 当 且 仅 当 时 取
等 号 , , 故 选 B
解 法 2 ( 极 化 恒 等 式 )
设 E F 的 中 点 为 M , 连 接 C M , 则 , 即 点 M 在 如 图 所 示 的 圆 弧 上 , 则
,故 选 B
本 题 也 可 用 三 角 换 元 法 解 决
例 3 , ( 2 0 1 3 浙 江 ) 设 , 是 边 A B 上 的 一 定 点 , 满 足 , 且 对 于 边 A B 上
任 一 点 P , 恒 有 , 则 ( )
A . B . C . D .
解 法 1 ( 坐 标 法 )
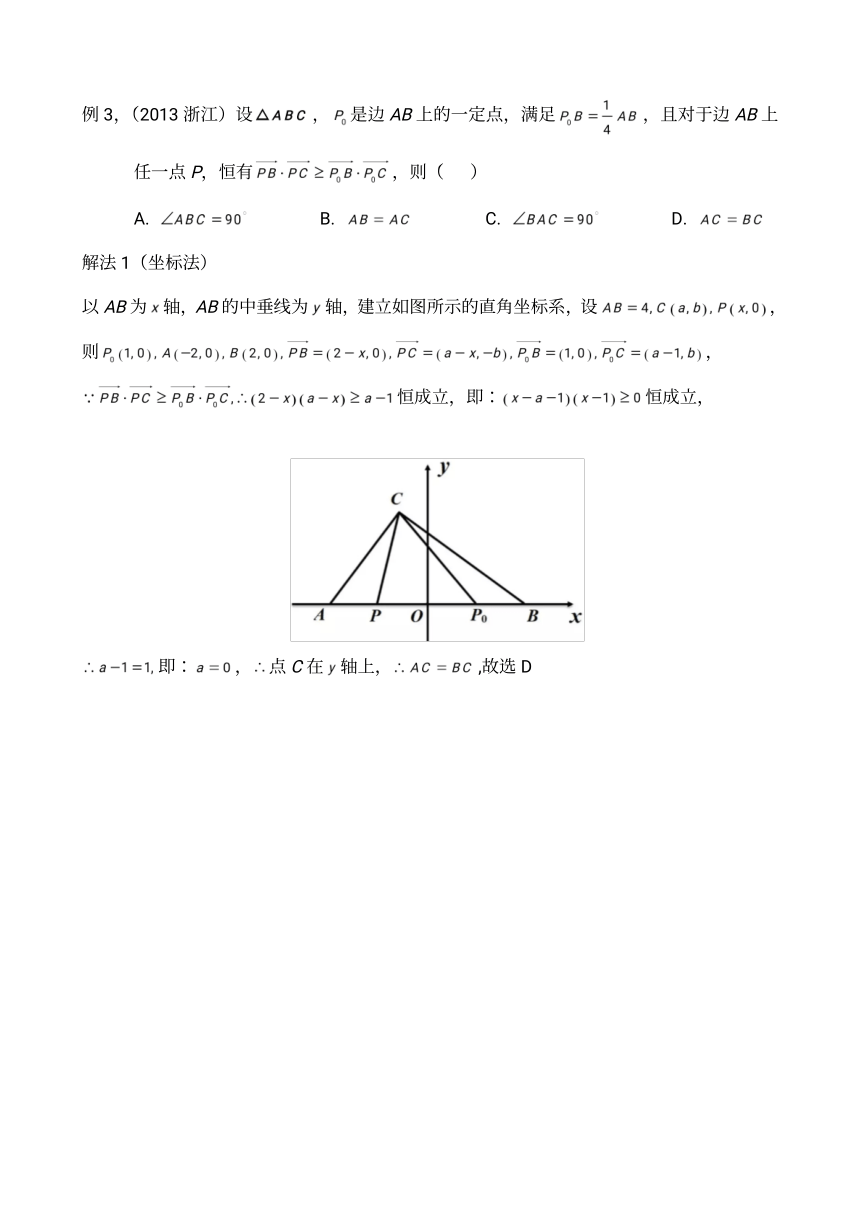
以 A B 为 轴 , A B 的 中 垂 线 为 轴 , 建 立 如 图 所 示 的 直 角 坐 标 系 , 设 ,
则 ,
恒 成 立 , 即 : 恒 成 立 ,
即 : , 点 C 在 轴 上 , ,故 选 D
解 法 2 ( 基 地 法 )
解 法 3 ( 极 化 恒 等 式 )
例 4 、 ( 2 0 1 6 江 苏 ) 如 图 , 在 中 , D 是 B C 的 中 点 , E , F
是 A D 上 的 两 个 三 等 分 点 , , 则
值 为
解 法 1 ( 坐 标 法 )
以 B C 为 , D 为 坐 标 原 点 ,
建 立 如 图 所 示 的 直 角 坐 标 系
解 法 2 ( 基 底 法 )
解 法 3 ( 极 化 恒 等 式 )
例 5 、( 2 0 1 8 宝 鸡 一 模 ) 直 线 与 圆 相 交 于 两 点 M ,N , 若 ,
P 为 圆 O 上 任 意 一 点 , 则 的 取 值 范 围 为
解 法 1 ( 坐 标 法 )
以 O 为 坐 标 原 点 , M N 的 平 行 线 为
轴 , 建 立 如 图 所 示 的 直 角 坐 标 系 ,
解 法 2 ( 基 底 法 )
解 法 3 ( 极 化 恒 等 式 )
例 6 , 如 图 , 已 知 B , D 是 直 角 C 两 边 上 的 动 点 ,
, ,
则 的 最 大 值 为
解 法 1 ( 坐 标 法 )
以 C 为 坐 标 原 点 , B C 为 轴 ,
建 立 如 图 所 示 的 直 角 坐 标 系 ,
解 法 2 ( 基 底 法 )
0 1 何 谓 极 化 恒 等 式
三 角 形 模 型 :
在 中 , D 为 B C 的 中 点 :
平 行 四 边 形 模 型
在 平 行 四 边 形 A B C D 中 :
0 2 极 化 恒 等 式 应 用
例 1 , ( 2 0 1 7 全 国 I I , 理 1 2 ) 已 知 是 边 长 为 2 的 等 边 三 角 形 , P 为 平 面 内 一 点 ,
则 的 最 小 值 是 ( )
A . B . C . D .
解 法 1 ( 坐 标 法 ) :
以 B C 所 在 直 线 为 轴 , B C 的 中 垂 线 轴 建 立 平 面 直 角 坐 标 系 , ,
设 , 则 ,
,
当 且 仅 当 , 即 , 取 得 最 小 值 .
解 法 2 ( 极 化 恒 等 式 ) :
设 B C 的 重 点 为 O , O C 的 中 点 为 M , 连 接 O P , P M ,
,
当 且 仅 当 M 与 P 重 合 始 去 等 号 .
例 2 在 中 , 已 知 是 的 中 点 , E , F 分 别 是 B C , A C 上 的
动 点 , 且 E F = 1 , 则 的 最 小 值 为 ( )
A . B . C . D .
解 法 1 ( 坐 标 法 )
以 A C 所 在 直 线 为 轴 , B C 所 在 直 线 为 轴 建 立 平 面 直 角 坐 标 系 , 则
设 则 , ,
,
由 柯 西 不 等 式 可 得 : , 即 , 当 且 仅 当 时 取
等 号 , , 故 选 B
解 法 2 ( 极 化 恒 等 式 )
设 E F 的 中 点 为 M , 连 接 C M , 则 , 即 点 M 在 如 图 所 示 的 圆 弧 上 , 则
,故 选 B
本 题 也 可 用 三 角 换 元 法 解 决
例 3 , ( 2 0 1 3 浙 江 ) 设 , 是 边 A B 上 的 一 定 点 , 满 足 , 且 对 于 边 A B 上
任 一 点 P , 恒 有 , 则 ( )
A . B . C . D .
解 法 1 ( 坐 标 法 )
以 A B 为 轴 , A B 的 中 垂 线 为 轴 , 建 立 如 图 所 示 的 直 角 坐 标 系 , 设 ,
则 ,
恒 成 立 , 即 : 恒 成 立 ,
即 : , 点 C 在 轴 上 , ,故 选 D
解 法 2 ( 基 地 法 )
解 法 3 ( 极 化 恒 等 式 )
例 4 、 ( 2 0 1 6 江 苏 ) 如 图 , 在 中 , D 是 B C 的 中 点 , E , F
是 A D 上 的 两 个 三 等 分 点 , , 则
值 为
解 法 1 ( 坐 标 法 )
以 B C 为 , D 为 坐 标 原 点 ,
建 立 如 图 所 示 的 直 角 坐 标 系
解 法 2 ( 基 底 法 )
解 法 3 ( 极 化 恒 等 式 )
例 5 、( 2 0 1 8 宝 鸡 一 模 ) 直 线 与 圆 相 交 于 两 点 M ,N , 若 ,
P 为 圆 O 上 任 意 一 点 , 则 的 取 值 范 围 为
解 法 1 ( 坐 标 法 )
以 O 为 坐 标 原 点 , M N 的 平 行 线 为
轴 , 建 立 如 图 所 示 的 直 角 坐 标 系 ,
解 法 2 ( 基 底 法 )
解 法 3 ( 极 化 恒 等 式 )
例 6 , 如 图 , 已 知 B , D 是 直 角 C 两 边 上 的 动 点 ,
, ,
则 的 最 大 值 为
解 法 1 ( 坐 标 法 )
以 C 为 坐 标 原 点 , B C 为 轴 ,
建 立 如 图 所 示 的 直 角 坐 标 系 ,
解 法 2 ( 基 底 法 )
同课章节目录
