22.1一元二次方程

(共13张PPT)
学 习 目 标：
1、了解一元二次方程的概念。
2、掌握一元二次方程一般形式，会把一元二次方程化成一般形式。
3、理解一元二次方程根的意义。
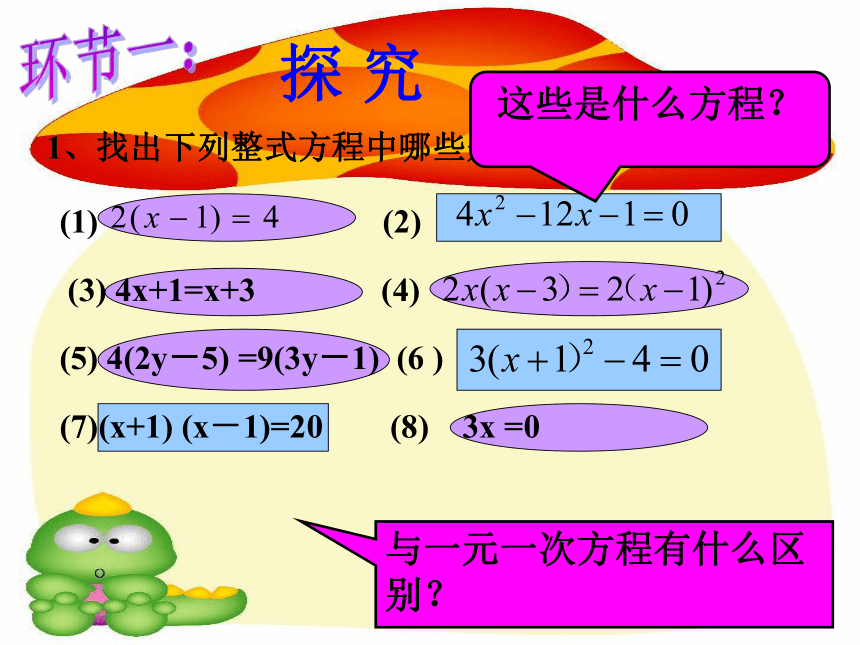
(1) (2)
(3) 4x+1=x+3 (4)
(5) 4(2y－5) =9(3y－1) (6 )
(7)(x+1) (x－1)=20 (8) 3x =0
探 究
1、找出下列整式方程中哪些是一元一次方程？
这些是什么方程？
与一元一次方程有什么区别？
归 纳 总 结:
定义：只含 有_________未知数，并且未知数的最高次数是____，这样的整式方程叫做一元二次方程.
通常可写成如下的一般形式：
(a、b、c是已知数，a___0)
一个
2
≠
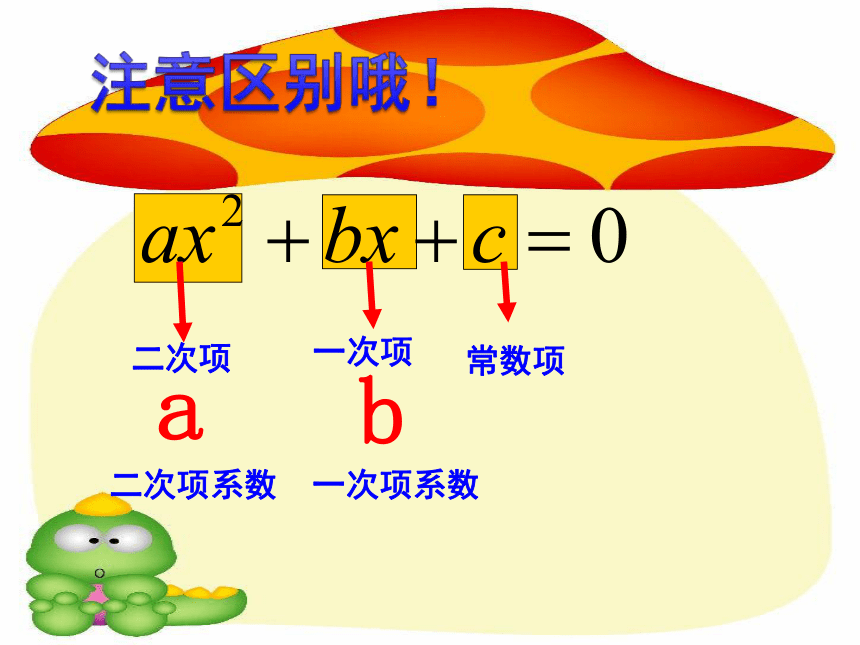
二次项
常数项
一次项
二次项系数　
一次项系数
a
b
自学指导
检 测一：
1、将下列方程化为一般形式，并分别指出它们的二次项系数、一次项系数和常数项：
（1） 化为一般形式_______________
二次项系数a=__、一次项系数b=___常数项c=__
（2） 化为一般形式________________
二次项系数a=__、一次项系数b=___常数项c=__
（3）x(2x－1)－3x(x－2)=0 化为一般形式:________
二次项系数a=__、一次项系数b=___常数项c=__
（4)2x(x－1)=3(x＋5)－4化为一般形式:_________
二次项系数a=__、一次项系数b=___常数项c=__
3
-1
-2
-7
2
3
-1
5
0
2
-5
-11
2、关于x的方程
是一元二次方程的条件是什么？
解：将 化成一般
形式为：
由题意可得：m-1 ≠0
∴ m≠1
3、关于的x方程 是一元二次方程，求k的值
解：∵方程 是一元 二次方程。
∴ ∴k=2或k=-2
又∵k-2 ≠ 0 ∴ k≠2
∴ k=-2
想一想
下面哪些数是方程 的解？
-4，-3，-2，-1，0，1，2，3，4
可以发现
当x=3或x=-2时，
所以x=3或x=-2是方程 的解。
一元二次方程的解也叫做一元二次方程的根。
检测二：
1、下面哪些数是方程 的解？
-4，-3，-2，-1，0，1，2，3，4
2、若x=1是 的一个根，则m=（ ） (A) 0　 (B) 1 　(C) 2 　(D) 3
D
我 的 收 获
1、一元二次方程的定义
2、一元二次方程的一般形式
3、一元二次方程的解
作　业
练习册34页：
C组：至少完成1、2、3、4
B组：在C组基础上做5、6、7、8、9
A组：再B组基础上做10、11、12、13