西师大版五年级数学下册课课练3.4 正方体和正方体体积计算长方体和同步练习(含答案)
文档属性
| 名称 | 西师大版五年级数学下册课课练3.4 正方体和正方体体积计算长方体和同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 140.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-22 00:00:00 | ||
图片预览



文档简介
西师大版五年级数学下册课课练
3.4 正方体和正方体体积计算长方体和同步练习
一、单选题(共8题;共16分)
1.体积是(?? )
A.?105 ????????? ??B.?108 ????????? ?????????C.?110 ???????????????????????????D.?120 ?
2.一个棱长4dm的正方体容器,注入3dm高的水,又投入1 dm3 的铅块,这时容器所装物体的体积是(?? )
A.???????? ????????????????????????B.?????????? ?C.????????????????????????????????D.?
3.一个长方体的长、宽、高分别为a米、b米、h米,如果高增加3米,那么新长方体的体积比原来增加了(??? )立方米。
A.?abh+3??????????????????? ????B.?3ab????????????????????????????????????C.?ab(h+3)
4.如果正方体的棱长缩小到原来的 13 ,那么它的体积缩小到原来的(??? )。
A.???????????? ??????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
5.将一个正方体铁块锻造成长方体铁块,则正方体和长方体比较( ??)
A.?表面积相等,体积不相等????????????B.?体积、表面积都相等???????????
?C.?体积相等,表面积不相等
6.把一根长2米的长方体木料锯成两段后,表面积增加了100平方厘米,它的体积是(?? )。
A.?200立方厘米???????????????????????????B.?10000立方厘米???????????????????????????C.?20立方分米
7.当长方体和正方体的棱长之和相等时,长方体的体积(??? )正方体的体积。
A.?大于????????? ??????B.?小于????????????? ?????C.?等于????????????????????????????????????D.?不确定
8.把一个正方体切成两个完全相同的长方体,这两个长方体的体积之和与原来的正方体相比(?? ),这两个长方体的表面积之和与原来的正方体相比(?? )。
A.?更大;更小?????? ??B.?更小;更大?? ????C.?一样大;更小? ??D.?一样大;更大
二、判断题
9.当正方体的棱长是6厘米时,它的体积和表面积相等。(??? )
10.判断下列说法是否正确。
(1)一瓶矿泉水的体积约是550L。(?? )
(2)棱长为6cm的正方体,它的表面积和体积相等。(?? )
(3)一个长方体木箱能装货8 m3 , 长方体木箱的体积就是8 m3。(?? )
(4)一个体积为1 dm3的物体,它的底面积一定是1 dm2。(?? )
(5)一个正方体的棱长扩大到原来的3倍,表面积就扩大到原来的9倍,体积就扩大到原来的27倍。(?? )
三、填空题
11.正方体的棱长扩大到原来的2倍,则表面积扩大到原来的________倍,体积扩大到原来的________倍。
12.一个正方体的框架是由36cm的钢条做成的,该正方体的底面积是________,表面积是________,体积是________。
13.一个长方体的棱长总和是48m,并且它的长、宽、高是三个连续自然数,这个长方体的表面积是________m2 , 体积是________m3。
14.一个正方体木块棱长为9dm,如果分割成棱长3dm的正方体可以分成________块。
15.一个长方体的棱长总和是72厘米,它的长、宽、高的比是4:3:2,它的表面积是________平方厘米,体积是________立方厘米。
16.一个表面积为54平方厘米的正方体,它的体积是________立方厘米。
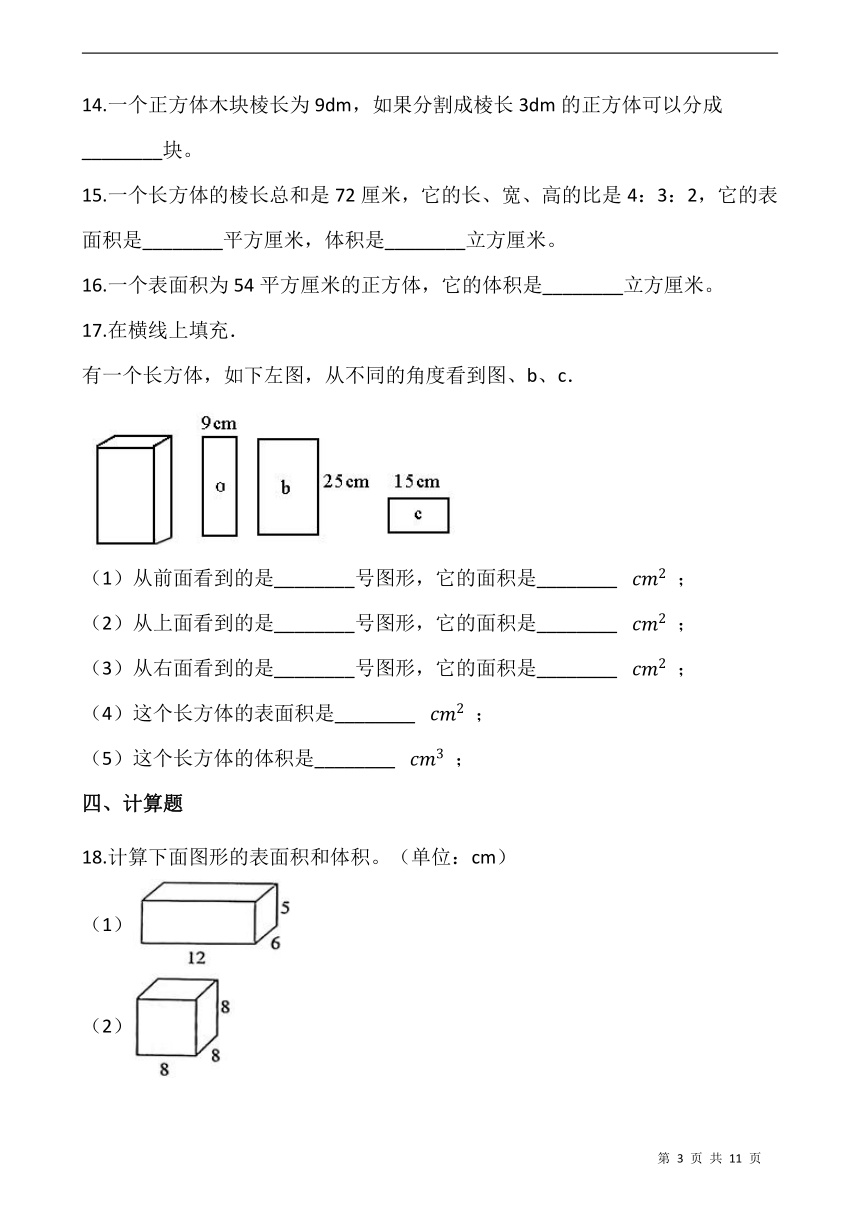
17.在横线上填充.
有一个长方体,如下左图,从不同的角度看到图、b、c.
(1)从前面看到的是________号图形,它的面积是________? cm2 ;
(2)从上面看到的是________号图形,它的面积是________? cm2 ;
(3)从右面看到的是________号图形,它的面积是________? cm2 ;
(4)这个长方体的表面积是________? cm2 ;
(5)这个长方体的体积是________? cm3 ;
四、计算题
18.计算下面图形的表面积和体积。(单位:cm)
(1)
(2)
五、解答题
19.光明小学准备用砖砌一面长20m,厚3dm,高2m的墙,每立方米的墙需要625块砖,学校砌这道墙需要多少块砖?
20.如下图,从长45cm、宽35cm的长方形纸板中,剪去4个边长为5cm的正方形,然后把它做成一个无盖的长方体盒子。这个盒子的容积是多少?
?
21.一根长2m的长方体木条,横截面是边长为5cm的正方形。制作400根这样的木条需要木材多少立方米?合多少立方分米?
22.一个长方体(如下图),如果高增加4厘米,就变成了棱长是10厘米的正方体。表面积和体积各增加了多少?
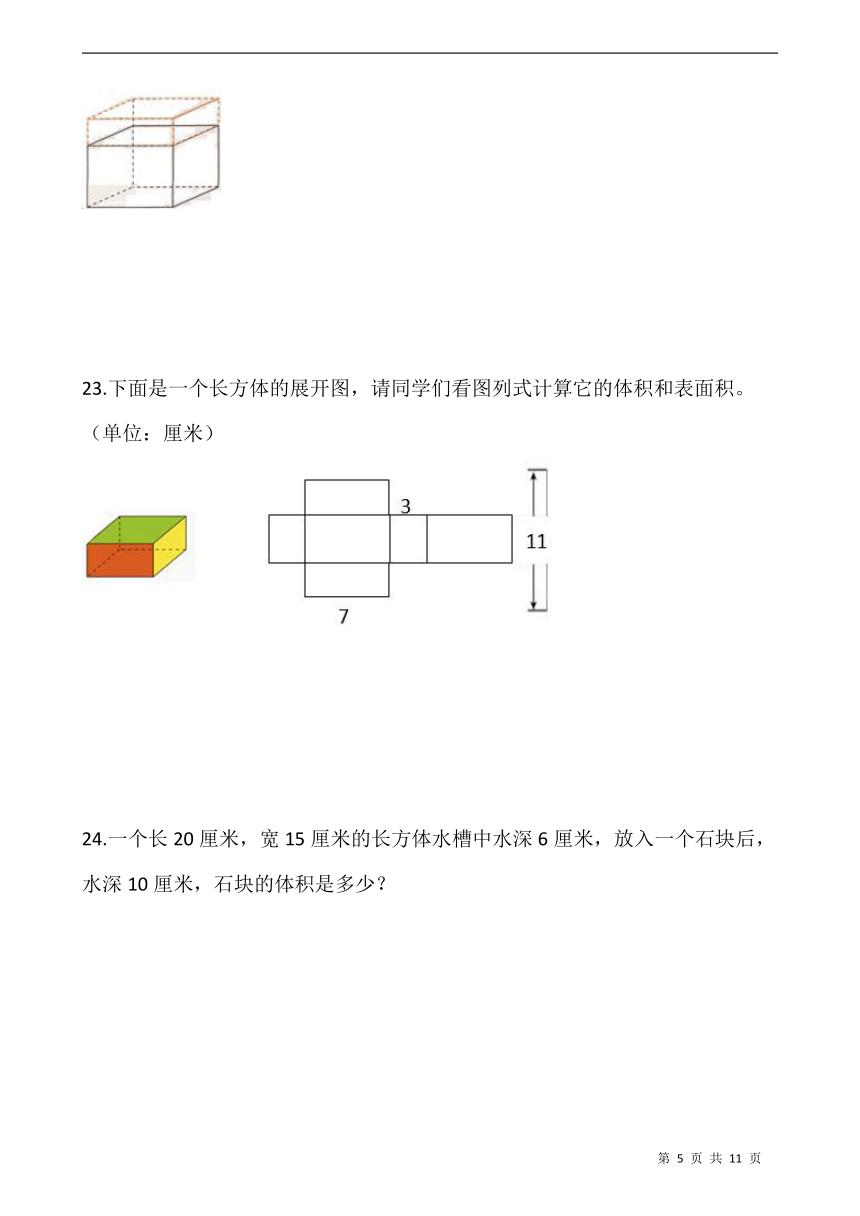
23.下面是一个长方体的展开图,请同学们看图列式计算它的体积和表面积。
(单位:厘米)
24.一个长20厘米,宽15厘米的长方体水槽中水深6厘米,放入一个石块后,水深10厘米,石块的体积是多少?
六、应用题
25.如图是一个长方体的空心管,掏空部分的长方体的长为10厘米,宽为7厘米。求这根空心管的体积是多少?如果每立分米重7.8千克,这根管子重多少千克?(单位:厘米)
26.有甲、乙两个水箱,从里面测量,甲水箱长12dm、宽8dm、高5dm,乙水箱长8dm、宽8dm、高6dm.甲水箱装满水,乙水箱空着.现将甲水箱里的一部分水抽到乙水箱中,使两箱水面高度一样.现在两个水箱的水面高多少分米?
27.用240厘米唱的铁丝做一个最大的正方体框架,然后用纸板将6个面包起来做一个正方体纸盒,至少需要多少平方厘米纸板?这个纸盒的体积是多少立方厘米?
28.上海世博会上的中国馆——“东方之冠”,造型独特,令世人瞩目。它的顶层是由底部的四根巨型钢筋混凝土核心筒托起,每个核心筒截面为18.6米×18.6米,高68米。这四根核心筒的体积一共是多少立方米?
答案解析部分
一、单选题
1.【答案】 B
2.【答案】 C
3.【答案】 B
4.【答案】 A
5.【答案】 C
6.【答案】 B
7.【答案】 B
8.【答案】 D
二、判断题
9.【答案】 错误
10.【答案】 (1)错误
(2)错误
(3)错误
(4)错误
(5)正确
三、填空题
11.【答案】 B;D
12.【答案】 9cm2;54cm2;27cm3
13.【答案】 94;60
14.【答案】 27
15.【答案】 208;192
16.【答案】 27
17.【答案】 (1)b;375
(2)c;135
(3)a;225
(4)1470
(5)3375
四、计算题
18.【答案】 (1)表面积:(12×6+6×5+12×5)×2=324(cm2)
体积:12×6×5=360(cm3)
(2)表面积: 8×8×6=384(cm2)
体积:8×8×8=512(cm3)
五、解答题
19.【答案】 解:3dm = 0.3m
20×0.3×2=12(m3)
12 ×625=7500(块)
答:学校砌这道墙需要7500块砖。
20.【答案】 解:(45-5×2)×(35-5×2)×5
=35×25×5
=4375(立方厘米)
答:这个盒子的容积是4375立方厘米。
21.【答案】 解:5÷100=0.05(m)
0.05×0.05×2×400
=0.0025×2×400
=0.005×400
=2(立方米)
=2000立方分米
答:制作400根这样的木条需要木材2立方米,合2000立方分米。
22.【答案】 解:长方体的长是10厘米、宽是10厘米,高是10-4=6厘米,
所以长方体的表面积=(10×10+10×6+10×6)×2
=(100+60+60)×2
=220×2
=440(平方厘米);
长方体的体积=10×10×6
=100×6
=600(立方厘米)。
答:长方体的表面积是440平方厘米,长方体的体积是600立方厘米。
23.【答案】 解:11-3-3=5(厘米)
3×5×7=245(立方厘米)
3×5×2+3×7×2+5×7×2=142(平方厘米)
答:这个长方体的体积是245立方厘米,表面积是142平方厘米。
24.【答案】 10-6=4(厘米)
20×15×4=1200(立方厘米)
?答:石块的体积是1200立方厘米。
六、应用题
25.【答案】 解:18×15×40-10×7×40=8000(立方厘米)
8000立方厘米=8立方分米
8×7.8=62.4(千克)
答:这根空心管的体积是8000立方厘米,这根管子重62.4千克。
26.【答案】 解:12×8×5÷(12×8+8×8)
=480÷(96+64)
=480÷160
=3(dm)
答:现在两个水箱的水面高是3dm。
27.【答案】 解:240÷12=20(厘米);20×20×6=2400(平方厘米);20×20×20=8000(立方厘米)
28.【答案】 解:18.6×18.6×68×4
=23525.28×4
=94101.12(立方米)
答:这四根核心筒的体积一共是94101.12立方米。
3.4 正方体和正方体体积计算长方体和同步练习
一、单选题(共8题;共16分)
1.体积是(?? )
A.?105 ????????? ??B.?108 ????????? ?????????C.?110 ???????????????????????????D.?120 ?
2.一个棱长4dm的正方体容器,注入3dm高的水,又投入1 dm3 的铅块,这时容器所装物体的体积是(?? )
A.???????? ????????????????????????B.?????????? ?C.????????????????????????????????D.?
3.一个长方体的长、宽、高分别为a米、b米、h米,如果高增加3米,那么新长方体的体积比原来增加了(??? )立方米。
A.?abh+3??????????????????? ????B.?3ab????????????????????????????????????C.?ab(h+3)
4.如果正方体的棱长缩小到原来的 13 ,那么它的体积缩小到原来的(??? )。
A.???????????? ??????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
5.将一个正方体铁块锻造成长方体铁块,则正方体和长方体比较( ??)
A.?表面积相等,体积不相等????????????B.?体积、表面积都相等???????????
?C.?体积相等,表面积不相等
6.把一根长2米的长方体木料锯成两段后,表面积增加了100平方厘米,它的体积是(?? )。
A.?200立方厘米???????????????????????????B.?10000立方厘米???????????????????????????C.?20立方分米
7.当长方体和正方体的棱长之和相等时,长方体的体积(??? )正方体的体积。
A.?大于????????? ??????B.?小于????????????? ?????C.?等于????????????????????????????????????D.?不确定
8.把一个正方体切成两个完全相同的长方体,这两个长方体的体积之和与原来的正方体相比(?? ),这两个长方体的表面积之和与原来的正方体相比(?? )。
A.?更大;更小?????? ??B.?更小;更大?? ????C.?一样大;更小? ??D.?一样大;更大
二、判断题
9.当正方体的棱长是6厘米时,它的体积和表面积相等。(??? )
10.判断下列说法是否正确。
(1)一瓶矿泉水的体积约是550L。(?? )
(2)棱长为6cm的正方体,它的表面积和体积相等。(?? )
(3)一个长方体木箱能装货8 m3 , 长方体木箱的体积就是8 m3。(?? )
(4)一个体积为1 dm3的物体,它的底面积一定是1 dm2。(?? )
(5)一个正方体的棱长扩大到原来的3倍,表面积就扩大到原来的9倍,体积就扩大到原来的27倍。(?? )
三、填空题
11.正方体的棱长扩大到原来的2倍,则表面积扩大到原来的________倍,体积扩大到原来的________倍。
12.一个正方体的框架是由36cm的钢条做成的,该正方体的底面积是________,表面积是________,体积是________。
13.一个长方体的棱长总和是48m,并且它的长、宽、高是三个连续自然数,这个长方体的表面积是________m2 , 体积是________m3。
14.一个正方体木块棱长为9dm,如果分割成棱长3dm的正方体可以分成________块。
15.一个长方体的棱长总和是72厘米,它的长、宽、高的比是4:3:2,它的表面积是________平方厘米,体积是________立方厘米。
16.一个表面积为54平方厘米的正方体,它的体积是________立方厘米。
17.在横线上填充.
有一个长方体,如下左图,从不同的角度看到图、b、c.
(1)从前面看到的是________号图形,它的面积是________? cm2 ;
(2)从上面看到的是________号图形,它的面积是________? cm2 ;
(3)从右面看到的是________号图形,它的面积是________? cm2 ;
(4)这个长方体的表面积是________? cm2 ;
(5)这个长方体的体积是________? cm3 ;
四、计算题
18.计算下面图形的表面积和体积。(单位:cm)
(1)
(2)
五、解答题
19.光明小学准备用砖砌一面长20m,厚3dm,高2m的墙,每立方米的墙需要625块砖,学校砌这道墙需要多少块砖?
20.如下图,从长45cm、宽35cm的长方形纸板中,剪去4个边长为5cm的正方形,然后把它做成一个无盖的长方体盒子。这个盒子的容积是多少?
?
21.一根长2m的长方体木条,横截面是边长为5cm的正方形。制作400根这样的木条需要木材多少立方米?合多少立方分米?
22.一个长方体(如下图),如果高增加4厘米,就变成了棱长是10厘米的正方体。表面积和体积各增加了多少?
23.下面是一个长方体的展开图,请同学们看图列式计算它的体积和表面积。
(单位:厘米)
24.一个长20厘米,宽15厘米的长方体水槽中水深6厘米,放入一个石块后,水深10厘米,石块的体积是多少?
六、应用题
25.如图是一个长方体的空心管,掏空部分的长方体的长为10厘米,宽为7厘米。求这根空心管的体积是多少?如果每立分米重7.8千克,这根管子重多少千克?(单位:厘米)
26.有甲、乙两个水箱,从里面测量,甲水箱长12dm、宽8dm、高5dm,乙水箱长8dm、宽8dm、高6dm.甲水箱装满水,乙水箱空着.现将甲水箱里的一部分水抽到乙水箱中,使两箱水面高度一样.现在两个水箱的水面高多少分米?
27.用240厘米唱的铁丝做一个最大的正方体框架,然后用纸板将6个面包起来做一个正方体纸盒,至少需要多少平方厘米纸板?这个纸盒的体积是多少立方厘米?
28.上海世博会上的中国馆——“东方之冠”,造型独特,令世人瞩目。它的顶层是由底部的四根巨型钢筋混凝土核心筒托起,每个核心筒截面为18.6米×18.6米,高68米。这四根核心筒的体积一共是多少立方米?
答案解析部分
一、单选题
1.【答案】 B
2.【答案】 C
3.【答案】 B
4.【答案】 A
5.【答案】 C
6.【答案】 B
7.【答案】 B
8.【答案】 D
二、判断题
9.【答案】 错误
10.【答案】 (1)错误
(2)错误
(3)错误
(4)错误
(5)正确
三、填空题
11.【答案】 B;D
12.【答案】 9cm2;54cm2;27cm3
13.【答案】 94;60
14.【答案】 27
15.【答案】 208;192
16.【答案】 27
17.【答案】 (1)b;375
(2)c;135
(3)a;225
(4)1470
(5)3375
四、计算题
18.【答案】 (1)表面积:(12×6+6×5+12×5)×2=324(cm2)
体积:12×6×5=360(cm3)
(2)表面积: 8×8×6=384(cm2)
体积:8×8×8=512(cm3)
五、解答题
19.【答案】 解:3dm = 0.3m
20×0.3×2=12(m3)
12 ×625=7500(块)
答:学校砌这道墙需要7500块砖。
20.【答案】 解:(45-5×2)×(35-5×2)×5
=35×25×5
=4375(立方厘米)
答:这个盒子的容积是4375立方厘米。
21.【答案】 解:5÷100=0.05(m)
0.05×0.05×2×400
=0.0025×2×400
=0.005×400
=2(立方米)
=2000立方分米
答:制作400根这样的木条需要木材2立方米,合2000立方分米。
22.【答案】 解:长方体的长是10厘米、宽是10厘米,高是10-4=6厘米,
所以长方体的表面积=(10×10+10×6+10×6)×2
=(100+60+60)×2
=220×2
=440(平方厘米);
长方体的体积=10×10×6
=100×6
=600(立方厘米)。
答:长方体的表面积是440平方厘米,长方体的体积是600立方厘米。
23.【答案】 解:11-3-3=5(厘米)
3×5×7=245(立方厘米)
3×5×2+3×7×2+5×7×2=142(平方厘米)
答:这个长方体的体积是245立方厘米,表面积是142平方厘米。
24.【答案】 10-6=4(厘米)
20×15×4=1200(立方厘米)
?答:石块的体积是1200立方厘米。
六、应用题
25.【答案】 解:18×15×40-10×7×40=8000(立方厘米)
8000立方厘米=8立方分米
8×7.8=62.4(千克)
答:这根空心管的体积是8000立方厘米,这根管子重62.4千克。
26.【答案】 解:12×8×5÷(12×8+8×8)
=480÷(96+64)
=480÷160
=3(dm)
答:现在两个水箱的水面高是3dm。
27.【答案】 解:240÷12=20(厘米);20×20×6=2400(平方厘米);20×20×20=8000(立方厘米)
28.【答案】 解:18.6×18.6×68×4
=23525.28×4
=94101.12(立方米)
答:这四根核心筒的体积一共是94101.12立方米。
