2020-2021学年七年级数学华东师大版下册 9.1 .3三角形的三边关系课件(16张ppt)
文档属性
| 名称 | 2020-2021学年七年级数学华东师大版下册 9.1 .3三角形的三边关系课件(16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 193.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-23 10:23:28 | ||
图片预览





文档简介
9.1 三角形
第5课时 三角形的三
边关系
第9章 多边形
导入新课
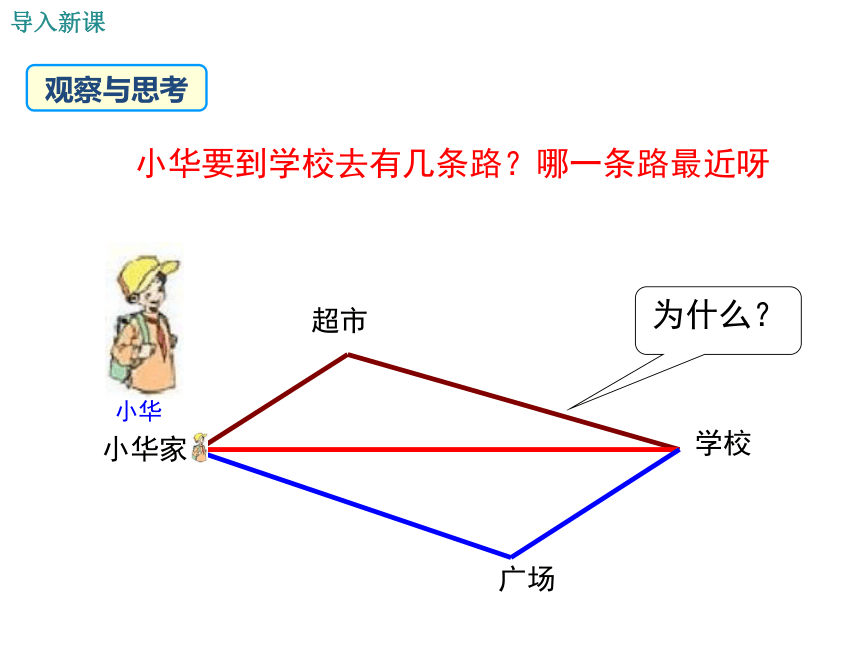
观察与思考
小华
为什么?
超市
学校
广场
小华家
小华要到学校去有几条路?哪一条路最近呀
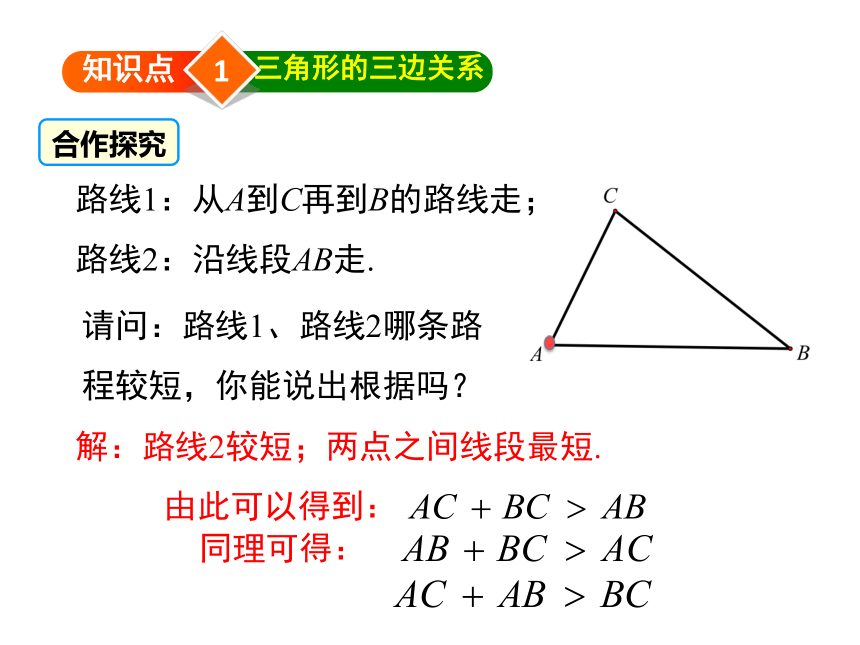
路线1:从A到C再到B的路线走;
路线2:沿线段AB走.
请问:路线1、路线2哪条路程较短,你能说出根据吗?
解:路线2较短;两点之间线段最短.
由此可以得到:
合作探究
1
知识点
三角形的三边关系
同理可得:
三角形任意两边的和大于第三边
想一想:由不等式的变形,三角形的两边之差与第三边有何关系?
三角形任意两边的差小于第三边
三角形三边的关系定理的理论根据是?
三角形的三边关系定理
两点之间,线段最短.
要点精析:
运用三角形的三边关系可以解决以下问题:
(1)判断三条已知线段能否组成一个三角形;
(2)已知三角形的两边长,确定第三边长的取值范围或
周长的取值范围;
(3)当三角形的边长用字母表示时,确定字母的取值范
围;
(4)证明一些线段的不等关系.
三角形三边关系:
两边之差<第三边<两边之和
例1
( )
B
已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为( )
A.7 B.8 C.9 D.10
例2
C
用一条长为21 cm的细绳围成一个三角形,能围成一边长是5 cm的等腰三角形吗?为什么?
例3
解:
当5 cm长的边是底边时,设腰长为x cm,
则 5+2x=21,
解得x=8.
当5 cm长的边是腰时,设底边长为y cm,
则 2×5+y=21,解得y=11.
因为5+5<11,不符合三角形的两边之和大于第
三边,所以不能围成腰长为5 cm的等腰三角形.
所以能围成底边长为5 cm的等腰三角形.
2
知识点
三角形的稳定性
用三根木条钉一个三角形,你会发现再也无法改
变这个三角形的形状和大小,也就是说,如果三角形
的三条边固定,那么三角形的形状和大小就完全确定
了. 三角形的这个性质叫做三角形的稳定性.
用四根木条钉一个四边形,你会发现这个四边形
的形状和大小都可以改变,这说明四边形不具有稳定
性.
1. 如果三角形的三条边固定,那么三角形的形状和大
小就完全确定了.三角形的这个性质叫做三角形的
稳定性.
2. 四边及四边以上的图形不具有稳定性,为保证其稳
定,常在多边形中构造三角形.
注意:稳定性是三角形的特性,其他图形都不具有
稳定性.
工人师傅在安装木制门框时,为防止变形常常像图中所示,钉上两条斜拉的木条,这样做的依据是( )
A.三角形的稳定性
B.两点之间线段最短
C.两点确定一条直线
D.垂线段最短
例4
A
要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架呢?六边形木架呢?n边形木架呢?
例5
解:
四边形木架至少要再钉上1根,五边形木架:2根,
六边形木架:3根,n边形木架:(n-3)根.
1.若一个三角形的两边长分别为3 cm,6 cm,则它的第三边的长可能是( )
A.2 cm B.3 cm C.6 cm D.9 cm
C
课堂练习
2、一个三角形两边的长分别为5 cm和3 cm,第三边的长是整数,且周长是偶数,则第三边的长是( )
A.2 cm或4 cm
B.4 cm或6 cm
C.4 cm
D.2 cm或6 cm
B
3、建高楼常需要用塔吊来吊建筑材料,如图所示,塔吊的上部是三角形结构,这是应用了三角形的哪个性质?
答:____________.(填“稳定性”
或“不稳定性”)
稳定性
三角形的三边关系
三角形的三边关系:任何两边的和大于第三边,任何两边的差小于第三边.
三角形
具有稳定性
课堂小结
第5课时 三角形的三
边关系
第9章 多边形
导入新课
观察与思考
小华
为什么?
超市
学校
广场
小华家
小华要到学校去有几条路?哪一条路最近呀
路线1:从A到C再到B的路线走;
路线2:沿线段AB走.
请问:路线1、路线2哪条路程较短,你能说出根据吗?
解:路线2较短;两点之间线段最短.
由此可以得到:
合作探究
1
知识点
三角形的三边关系
同理可得:
三角形任意两边的和大于第三边
想一想:由不等式的变形,三角形的两边之差与第三边有何关系?
三角形任意两边的差小于第三边
三角形三边的关系定理的理论根据是?
三角形的三边关系定理
两点之间,线段最短.
要点精析:
运用三角形的三边关系可以解决以下问题:
(1)判断三条已知线段能否组成一个三角形;
(2)已知三角形的两边长,确定第三边长的取值范围或
周长的取值范围;
(3)当三角形的边长用字母表示时,确定字母的取值范
围;
(4)证明一些线段的不等关系.
三角形三边关系:
两边之差<第三边<两边之和
例1
( )
B
已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为( )
A.7 B.8 C.9 D.10
例2
C
用一条长为21 cm的细绳围成一个三角形,能围成一边长是5 cm的等腰三角形吗?为什么?
例3
解:
当5 cm长的边是底边时,设腰长为x cm,
则 5+2x=21,
解得x=8.
当5 cm长的边是腰时,设底边长为y cm,
则 2×5+y=21,解得y=11.
因为5+5<11,不符合三角形的两边之和大于第
三边,所以不能围成腰长为5 cm的等腰三角形.
所以能围成底边长为5 cm的等腰三角形.
2
知识点
三角形的稳定性
用三根木条钉一个三角形,你会发现再也无法改
变这个三角形的形状和大小,也就是说,如果三角形
的三条边固定,那么三角形的形状和大小就完全确定
了. 三角形的这个性质叫做三角形的稳定性.
用四根木条钉一个四边形,你会发现这个四边形
的形状和大小都可以改变,这说明四边形不具有稳定
性.
1. 如果三角形的三条边固定,那么三角形的形状和大
小就完全确定了.三角形的这个性质叫做三角形的
稳定性.
2. 四边及四边以上的图形不具有稳定性,为保证其稳
定,常在多边形中构造三角形.
注意:稳定性是三角形的特性,其他图形都不具有
稳定性.
工人师傅在安装木制门框时,为防止变形常常像图中所示,钉上两条斜拉的木条,这样做的依据是( )
A.三角形的稳定性
B.两点之间线段最短
C.两点确定一条直线
D.垂线段最短
例4
A
要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架呢?六边形木架呢?n边形木架呢?
例5
解:
四边形木架至少要再钉上1根,五边形木架:2根,
六边形木架:3根,n边形木架:(n-3)根.
1.若一个三角形的两边长分别为3 cm,6 cm,则它的第三边的长可能是( )
A.2 cm B.3 cm C.6 cm D.9 cm
C
课堂练习
2、一个三角形两边的长分别为5 cm和3 cm,第三边的长是整数,且周长是偶数,则第三边的长是( )
A.2 cm或4 cm
B.4 cm或6 cm
C.4 cm
D.2 cm或6 cm
B
3、建高楼常需要用塔吊来吊建筑材料,如图所示,塔吊的上部是三角形结构,这是应用了三角形的哪个性质?
答:____________.(填“稳定性”
或“不稳定性”)
稳定性
三角形的三边关系
三角形的三边关系:任何两边的和大于第三边,任何两边的差小于第三边.
三角形
具有稳定性
课堂小结
