2020-2021学年七年级数学华东师大版下册第9章 多边形小结与复习课件(22张ppt)
文档属性
| 名称 | 2020-2021学年七年级数学华东师大版下册第9章 多边形小结与复习课件(22张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 234.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 08:41:28 | ||
图片预览





文档简介
小结与复习
第9章 多边形
要点梳理
一、三角形的分类
按边分
按角分
不等边三角形
等腰三角形
腰和底不等的等腰三角形
等边三角形
直角三角形
锐角三角形
钝角三角形
例1、三角形是( )
A.连结任意三点组成的图形
B.由不在同一条直线上的三条线段首尾顺次相结所组成的图形
C.由三条线段组成的图形
D.以上说法均不正确
B
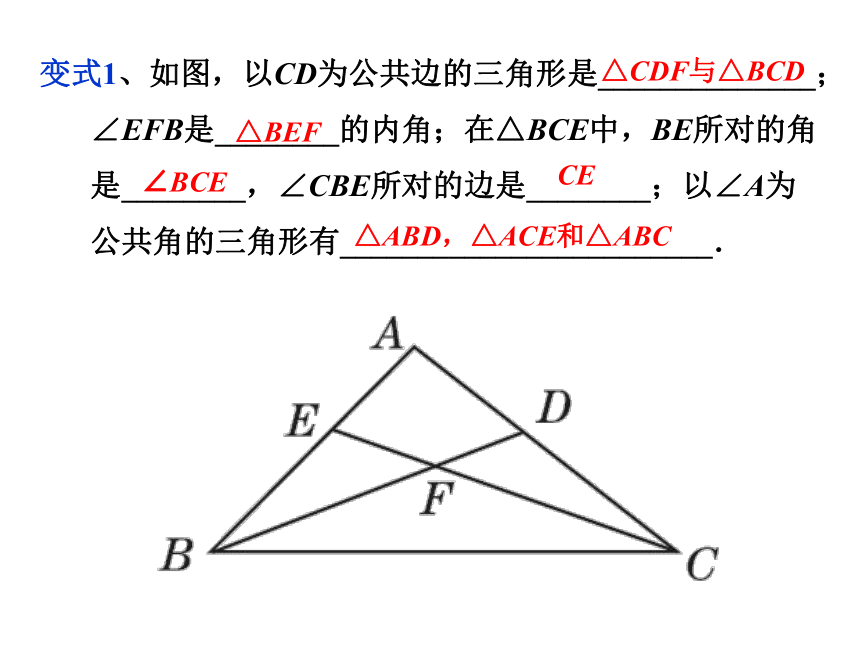
变式1、如图,以CD为公共边的三角形是______________;∠EFB是________的内角;在△BCE中,BE所对的角是________,∠CBE所对的边是________;以∠A为公共角的三角形有________________________.
△CDF与△BCD
△BEF
∠BCE
CE
△ABD,△ACE和△ABC
注意:① 三角形的高是线段;
② 锐角三角形三条高全在三角形的内部;
直角三角形有两条高是直角边,另一条在内部;
钝角三角形有两条高在三角形外,另一条在内部.
③ 三角形三条高所在直线交于一点.
1.三角形的高:从三角形的一个顶点向它的对边所在 的直线作垂线,顶点和垂足之间的线段.
表示法:① AD是△ABC的边BC上的高;
② AD⊥BC于D;
③∠ADB=∠ADC=90°.
二、三角形的高、中线、角平分线:
注意:①三角形的中线是线段;
②三角形三条中线全在三角形的内部;
③三角形三条中线交于三角形内部一点;
④中线把三角形分成两个面积相等的三角形.
2.三角形的中线:连接一个顶点和它对边中点的线段.
表示法:
① AD是△ABC的边BC上的中线;
② BD=DC= BC.
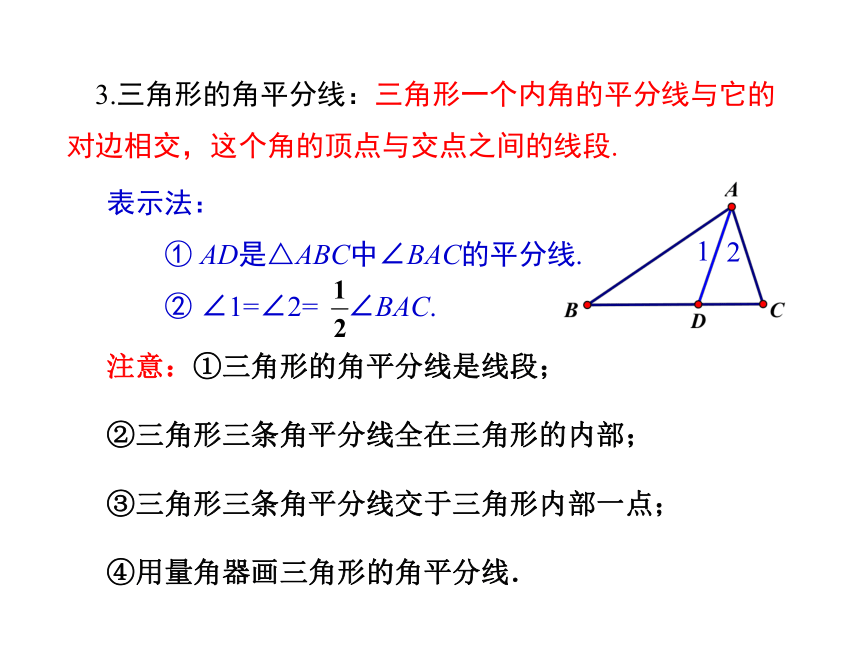
注意:①三角形的角平分线是线段;
②三角形三条角平分线全在三角形的内部;
③三角形三条角平分线交于三角形内部一点;
④用量角器画三角形的角平分线.
3.三角形的角平分线:三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段.
表示法:
① AD是△ABC中∠BAC的平分线.
② ∠1=∠2= ∠BAC.
1
2
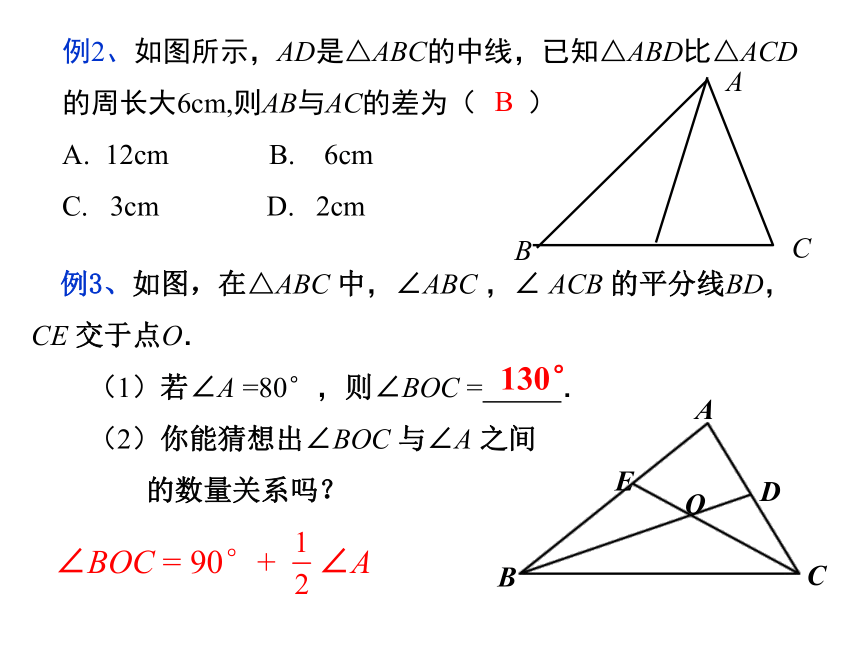
例2、如图所示,AD是△ABC的中线,已知△ABD比△ACD
的周长大6cm,则AB与AC的差为( )
12cm B. 6cm
C. 3cm D. 2cm
A
B
C
B
例3、如图,在△ABC 中,∠ABC ,∠ ACB 的平分线BD,CE 交于点O.
(1)若∠A =80°,则∠BOC = .
(2)你能猜想出∠BOC 与∠A 之间
的数量关系吗?
130°
∠BOC = 90°+ ∠A
A
B
C
O
E
D
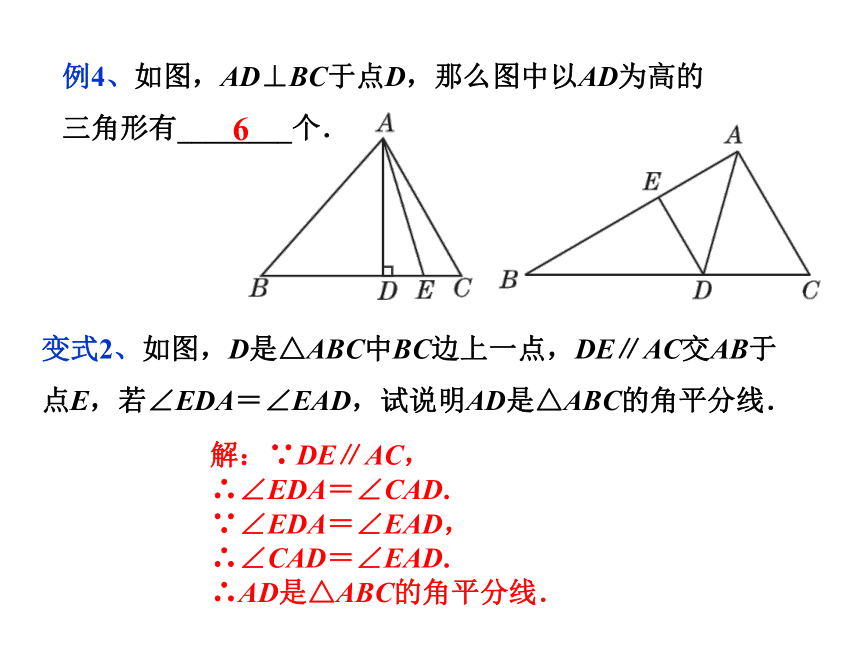
例4、如图,AD⊥BC于点D,那么图中以AD为高的
三角形有________个.
6
变式2、如图,D是△ABC中BC边上一点,DE∥AC交AB于点E,若∠EDA=∠EAD,试说明AD是△ABC的角平分线.
解:∵DE∥AC,
∴∠EDA=∠CAD.
∵∠EDA=∠EAD,
∴∠CAD=∠EAD.
∴AD是△ABC的角平分线.
变式3、如图所示,已知AD、AE分别是△ABC的高和中线,AB=6 cm,AC=8 cm,BC=10 cm,∠CAB=90°.
试求:(1)AD的长;
(2)△ABE的面积
三角形的内角和定理:三角形的内角和等于180°.
三、三角形内角和与外角和
推论:三角形的一个外角等于与它不相邻的两个内角的和,并且大于和它不相邻的任何一个内角.
三角形的外角和定理:三角形的外角和等于360°.
例5.根据下列条件,判断△ABC的形状.
(1)∠A=40°,∠B=80°;
(2)∠A:∠B:∠C=2:3:7.
解:(1)∠C=180°-∠A-∠B=60°,∵40°<60°<80°<90°,
∴△ABC是锐角三角形.
(2)设∠A=2x,∠B=3x,∠C=7x,
则2x+3x+7x=180°,
解得 x=15°.
∴∠C=7×15°=105°.
∴△ABC是钝角三角形.
例6、如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35° B.95° C.85° D.75°
C
变式4、如图,在直角三角形ABC中,∠ACB=90°,
∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F.求∠F的度数.
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°-65°=25°.
∵DF∥BE,∴∠F=∠CEB=25°.
注意:
1.三边关系的依据是:两点之间线段最短.
2.判断三条线段能否构成三角形的方法:只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
3.三角形第三边的取值范围是:
两边之差<第三边<两边之和
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边.
四、三角形的三边关系
例7、下列长度的三条线段,能组成三角形的是( )
A.3,4,8 B.5,6,10
C.5,5,11 D.5,6,11
B
例8、已知等腰三角形两边的长分别为3和7, 则此等腰三角形的周长为( )
A.13 B.17
C.13或17 D.13或10
B
变式5、等腰三角形的两边长a、b满足|a-4|+(b-9)2=0,
求这个等腰三角形的周长.
解:∵|a-4|+(b-9)2=0,
∴|a-4|=0,(b-9)2=0.
∴a=4,b=9.
若腰长为4,则4+4<9,不能构成三角形.
若腰长为9,则9+4>9,能构成三角形,
∴这个等腰三角形的周长为9+9+4=22.
五、多边形的性质
多边形的内角和定理:多边形的内角和等于(n-2) ×180 °
多边形的外角和定理:多边形的外角和等于 360 °
正多边形的性质:各边都相等,各内角也都相等
正多边形每个内角的度数是
正多边形每个外角的度数是
用相同正多边形可以铺满地面的条件:
正多边形的每个内角都能被360o 整除.
用多种正多边形可以拼成平面的条件:
围绕一点拼在一起的多种正多边形的内角之和为360?.
例9、如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11 C.12 D.13
C
例10、若正多边形的内角和是540°,则该正多边形的一个外角为( )
A.45° B.60° C.72° D.90°
C
变式6、已知一个多边形的每个外角都是其相邻内角度数的 ,
求这个多边形的边数.
解、 设此多边形的外角的度数为x,内角的度数为4x,
则x+4x=180°,
解得 x=36°.
∴边数n=360°÷36°=10.
三角形
与三角形有关的线段
三角形内角和:180°
三角形外角和:360°
三角形的边:三边关系定理
高线
中线:把三角形面积平分
角平分线
与三角形有关的角
内角与外角关系
三角形的分类
多边形
定义
多边形的内外角和
内角和:(n-2) ×180 °
外角和:360 °
对角线
多边形转化为三角形和
四边形的重要辅助线
正多边形
内角= ;外角=
课堂小结
第9章 多边形
要点梳理
一、三角形的分类
按边分
按角分
不等边三角形
等腰三角形
腰和底不等的等腰三角形
等边三角形
直角三角形
锐角三角形
钝角三角形
例1、三角形是( )
A.连结任意三点组成的图形
B.由不在同一条直线上的三条线段首尾顺次相结所组成的图形
C.由三条线段组成的图形
D.以上说法均不正确
B
变式1、如图,以CD为公共边的三角形是______________;∠EFB是________的内角;在△BCE中,BE所对的角是________,∠CBE所对的边是________;以∠A为公共角的三角形有________________________.
△CDF与△BCD
△BEF
∠BCE
CE
△ABD,△ACE和△ABC
注意:① 三角形的高是线段;
② 锐角三角形三条高全在三角形的内部;
直角三角形有两条高是直角边,另一条在内部;
钝角三角形有两条高在三角形外,另一条在内部.
③ 三角形三条高所在直线交于一点.
1.三角形的高:从三角形的一个顶点向它的对边所在 的直线作垂线,顶点和垂足之间的线段.
表示法:① AD是△ABC的边BC上的高;
② AD⊥BC于D;
③∠ADB=∠ADC=90°.
二、三角形的高、中线、角平分线:
注意:①三角形的中线是线段;
②三角形三条中线全在三角形的内部;
③三角形三条中线交于三角形内部一点;
④中线把三角形分成两个面积相等的三角形.
2.三角形的中线:连接一个顶点和它对边中点的线段.
表示法:
① AD是△ABC的边BC上的中线;
② BD=DC= BC.
注意:①三角形的角平分线是线段;
②三角形三条角平分线全在三角形的内部;
③三角形三条角平分线交于三角形内部一点;
④用量角器画三角形的角平分线.
3.三角形的角平分线:三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段.
表示法:
① AD是△ABC中∠BAC的平分线.
② ∠1=∠2= ∠BAC.
1
2
例2、如图所示,AD是△ABC的中线,已知△ABD比△ACD
的周长大6cm,则AB与AC的差为( )
12cm B. 6cm
C. 3cm D. 2cm
A
B
C
B
例3、如图,在△ABC 中,∠ABC ,∠ ACB 的平分线BD,CE 交于点O.
(1)若∠A =80°,则∠BOC = .
(2)你能猜想出∠BOC 与∠A 之间
的数量关系吗?
130°
∠BOC = 90°+ ∠A
A
B
C
O
E
D
例4、如图,AD⊥BC于点D,那么图中以AD为高的
三角形有________个.
6
变式2、如图,D是△ABC中BC边上一点,DE∥AC交AB于点E,若∠EDA=∠EAD,试说明AD是△ABC的角平分线.
解:∵DE∥AC,
∴∠EDA=∠CAD.
∵∠EDA=∠EAD,
∴∠CAD=∠EAD.
∴AD是△ABC的角平分线.
变式3、如图所示,已知AD、AE分别是△ABC的高和中线,AB=6 cm,AC=8 cm,BC=10 cm,∠CAB=90°.
试求:(1)AD的长;
(2)△ABE的面积
三角形的内角和定理:三角形的内角和等于180°.
三、三角形内角和与外角和
推论:三角形的一个外角等于与它不相邻的两个内角的和,并且大于和它不相邻的任何一个内角.
三角形的外角和定理:三角形的外角和等于360°.
例5.根据下列条件,判断△ABC的形状.
(1)∠A=40°,∠B=80°;
(2)∠A:∠B:∠C=2:3:7.
解:(1)∠C=180°-∠A-∠B=60°,∵40°<60°<80°<90°,
∴△ABC是锐角三角形.
(2)设∠A=2x,∠B=3x,∠C=7x,
则2x+3x+7x=180°,
解得 x=15°.
∴∠C=7×15°=105°.
∴△ABC是钝角三角形.
例6、如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35° B.95° C.85° D.75°
C
变式4、如图,在直角三角形ABC中,∠ACB=90°,
∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F.求∠F的度数.
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°-65°=25°.
∵DF∥BE,∴∠F=∠CEB=25°.
注意:
1.三边关系的依据是:两点之间线段最短.
2.判断三条线段能否构成三角形的方法:只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
3.三角形第三边的取值范围是:
两边之差<第三边<两边之和
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边.
四、三角形的三边关系
例7、下列长度的三条线段,能组成三角形的是( )
A.3,4,8 B.5,6,10
C.5,5,11 D.5,6,11
B
例8、已知等腰三角形两边的长分别为3和7, 则此等腰三角形的周长为( )
A.13 B.17
C.13或17 D.13或10
B
变式5、等腰三角形的两边长a、b满足|a-4|+(b-9)2=0,
求这个等腰三角形的周长.
解:∵|a-4|+(b-9)2=0,
∴|a-4|=0,(b-9)2=0.
∴a=4,b=9.
若腰长为4,则4+4<9,不能构成三角形.
若腰长为9,则9+4>9,能构成三角形,
∴这个等腰三角形的周长为9+9+4=22.
五、多边形的性质
多边形的内角和定理:多边形的内角和等于(n-2) ×180 °
多边形的外角和定理:多边形的外角和等于 360 °
正多边形的性质:各边都相等,各内角也都相等
正多边形每个内角的度数是
正多边形每个外角的度数是
用相同正多边形可以铺满地面的条件:
正多边形的每个内角都能被360o 整除.
用多种正多边形可以拼成平面的条件:
围绕一点拼在一起的多种正多边形的内角之和为360?.
例9、如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11 C.12 D.13
C
例10、若正多边形的内角和是540°,则该正多边形的一个外角为( )
A.45° B.60° C.72° D.90°
C
变式6、已知一个多边形的每个外角都是其相邻内角度数的 ,
求这个多边形的边数.
解、 设此多边形的外角的度数为x,内角的度数为4x,
则x+4x=180°,
解得 x=36°.
∴边数n=360°÷36°=10.
三角形
与三角形有关的线段
三角形内角和:180°
三角形外角和:360°
三角形的边:三边关系定理
高线
中线:把三角形面积平分
角平分线
与三角形有关的角
内角与外角关系
三角形的分类
多边形
定义
多边形的内外角和
内角和:(n-2) ×180 °
外角和:360 °
对角线
多边形转化为三角形和
四边形的重要辅助线
正多边形
内角= ;外角=
课堂小结
