2020--2021学年华东师大版八年级数学下册17.5.1 一次函数与二元一次方程(组)课件(19张ppt)
文档属性
| 名称 | 2020--2021学年华东师大版八年级数学下册17.5.1 一次函数与二元一次方程(组)课件(19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 217.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 08:50:41 | ||
图片预览



文档简介
17.5 实践与探究
第1课时 一次函数与二元
一次方程(组)
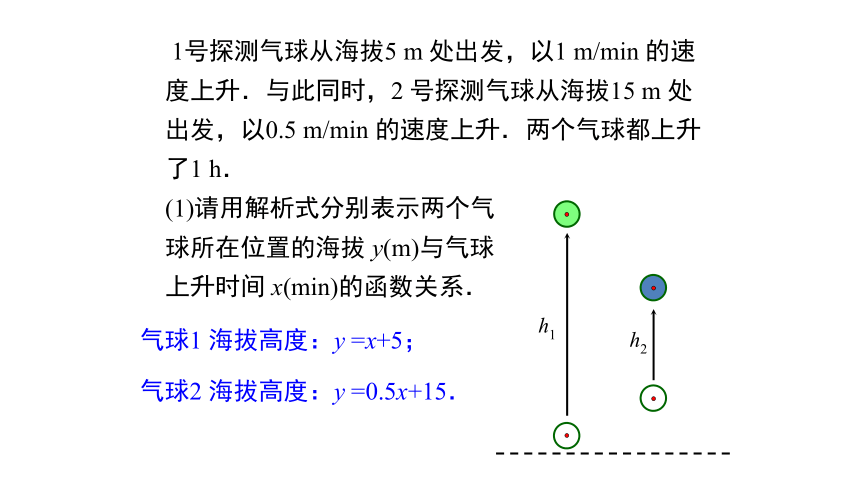
1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
(1)请用解析式分别表示两个气
球所在位置的海拔 y(m)与气球
上升时间 x(min)的函数关系.
h1
h2
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
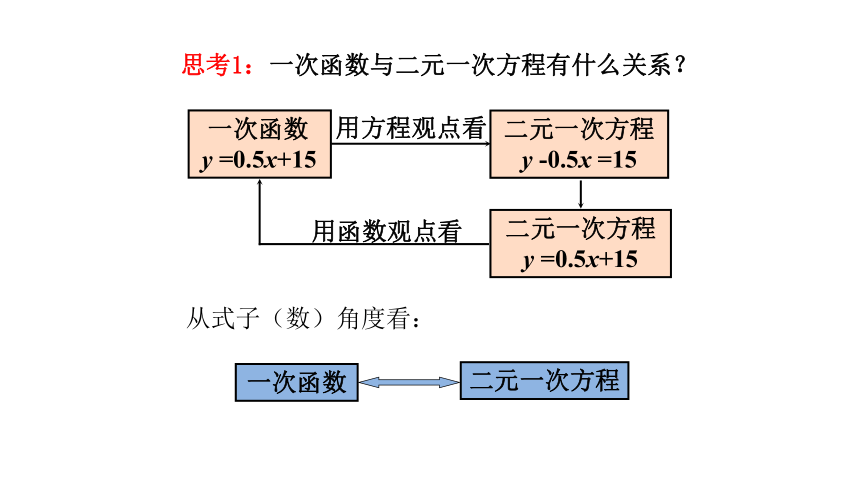
思考1:一次函数与二元一次方程有什么关系?
一次函数
二元一次方程
一次函数
y =0.5x+15
二元一次方程
y -0.5x =15
二元一次方程
y =0.5x+15
用方程观点看
用函数观点看
从式子(数)角度看:
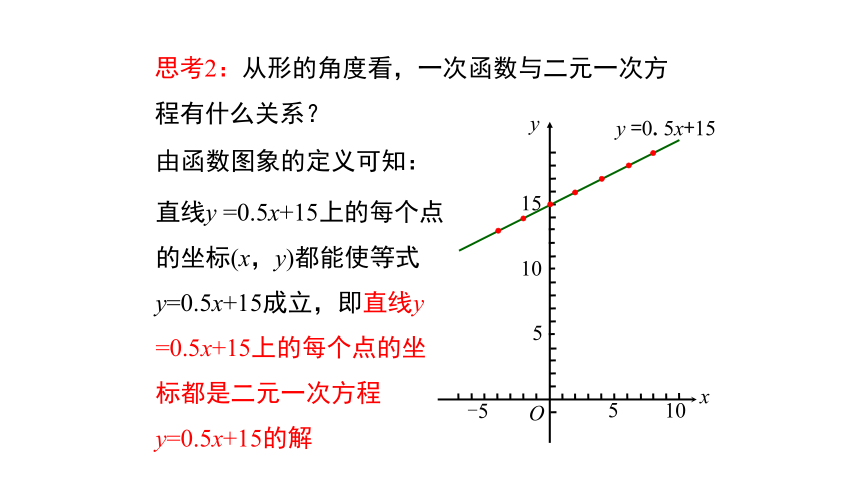
由函数图象的定义可知:
直线y =0.5x+15上的每个点的坐标(x,y)都能使等式y=0.5x+15成立,即直线y =0.5x+15上的每个点的坐标都是二元一次方程y=0.5x+15的解
思考2:从形的角度看,一次函数与二元一次方程有什么关系?
15
10
5
-5
5
10
O
x
y
y =0.5x+15
一次函数与二元一次方程的关系
由于任意一个二元一次方程都可以转化为y=kx+b的
形式,因此有:
(1)二元一次方程 一次函数 一条直线;
(2)二元一次方程的解 一次函数两变量的值 直
线上的点的坐标.
对应
对应
即为
即为
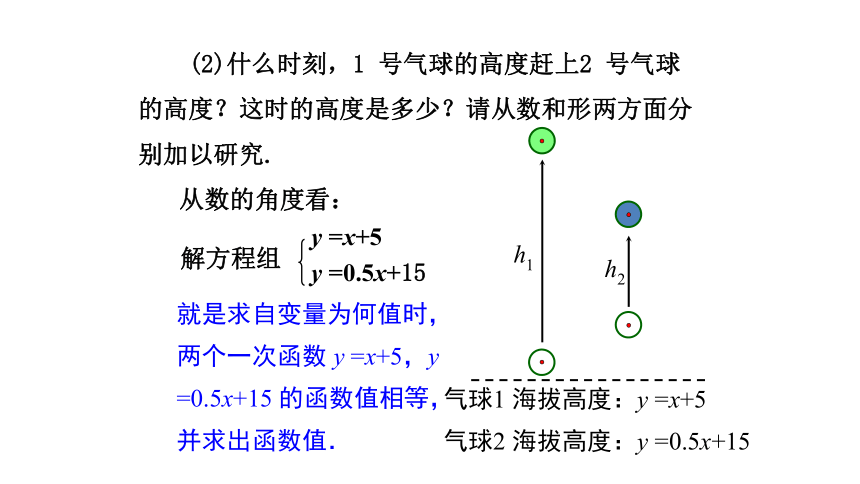
从数的角度看:
就是求自变量为何值时,两个一次函数 y =x+5,y =0.5x+15 的函数值相等,并求出函数值.
解方程组
y =x+5
y =0.5x+15
h1
h2
(2)什么时刻,1 号气球的高度赶上2 号气球的高度?这时的高度是多少?请从数和形两方面分别加以研究.
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
二元一次方程
组的解就是相应的
两个一次函数图象
的交点坐标.
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
从形的角度看,二元一次方程组与一次函数有什么关系?
1. 一次函数与二元一次方程组:
(1)二元一次方程组与一次函数的对应关系:
二元一次方程组 两个一次函数 两条直线;
二元一次方程组的解 两个一次函数值相等时的自变量值及函数值 两条直线的交点坐标.
(2)两直线交点个数与二元一次方程组解的个数的关系:
两条直线有交点(相交)?方程组只有一个解;
两条直线无交点(平行)?方程组无解;
两条直线是同一直线(重合)?方程组有无数个解.
对应
对应
即为
即为
总结
(3)用一次函数图象法解二元一次方程组的步骤:
①将方程组中每个方程分别转化成一次函数表达式;
②在同一坐标系中分别画出转化后的两个一次函数
的图象;
③根据两个函数图象的交点坐标写出方程组的解.
2. 易错警示:
对两直线交点与二元一次方程组的解的理解不透彻
而出错.
如图所示的四条直线,其中直线上每个点的坐标都是二元一次方程x-2y=2的解的是( )
例1
C
如图,一次函数y=ax+b与y=cx+d的图象交于点P,则方程组 的解是多少?
解:此方程组的解是
1
2
3
-1
-2
-3
-1
-3
-4
-5
2
O
-2
1
4
-6
x
y
P
y=ax+b
y=cx+d
例2
如图,在平面直角坐标系xOy中,
已知正比例函数y= x与一次函
数y=-x+7的图象交于点A.
(1)求点A的坐标;
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位
于点A的右侧),分别交y= x和y=-x+7的图象于
点B,C,连接OC,若BC=7,求△OBC的面积.
例3
(1)由题意得 解得
所以点A的坐标为(4,3).
(2)因为P(a,0),所以B ,
C(a,-a+7),
所以BC= a-(-a+7)= a-7,
所以 a-7=7,解得a=8.
所以S三角形OBC= BC·OP= ×7×8=28.
解:
已知一次函数y=ax+2与y=kx+b的
图象如图,且方程组
的解为 点B的坐标为(0,-1),
请你确定这两个一次函数的表达式.
例4
∵方程组 的解为
∴交点A的坐标为(2,1),
∴2a+2=1,解得a=- .
又∵函数y=kx+b的图象过交点A(2,1)和点B(0,-1)
∴ 解得
∴这两个一次函数的表达式分别为y=- x+2, y=x-1.
解:
1、直线y=kx+b(k≠0)对应的表达式就是一个关于x,
y的__________方程;以关于x,y的二元一次方程
y-kx=b(k≠0)的解为坐标的点组成的图象就是一
次函数______________的图象.
二元一次
y=kx+b(k≠0)
课堂练习
2、以下四条直线,其中直线上每个点的坐标都是二元一次方程x-2y=2的解的是( )
A B C D
C
3、已知 的解为 则直线
y=ax+b与y=-cx+d的交点坐标为( )
A.(1,2) B.(-1,2)
C.(1,-2) D.(-1,-2)
A
4、在平面直角坐标系中,点A,B的坐标分别为
(m,3),(3m-1,3),若线段AB与直线y=2x+1相交,则m的取值范围为___________.
1.一次函数与二元一次方程之间的区别和联系:
区别:(1)二元一次方程有两个未知数,而一次函数有两个变量;
(2)二元一次方程是用一个等式表示两个未知数的关系,而一次函数既可以用一个等式表示两个变量之间的关系,又可以用表格或图象来表示两个变量之间的关系.
联系:在直角坐标系中分别描出以二元一次方程的解为坐标的点,这些点都在相应的一次函数的图象上.
2. 求两直线的交点坐标方法是:联立两直线的解析式组成方程组,方程组的解就是交点的纵横坐标. 当两直线平行时,k相等,且方程组无解.
第1课时 一次函数与二元
一次方程(组)
1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.与此同时,2 号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升.两个气球都上升了1 h.
(1)请用解析式分别表示两个气
球所在位置的海拔 y(m)与气球
上升时间 x(min)的函数关系.
h1
h2
气球1 海拔高度:y =x+5;
气球2 海拔高度:y =0.5x+15.
思考1:一次函数与二元一次方程有什么关系?
一次函数
二元一次方程
一次函数
y =0.5x+15
二元一次方程
y -0.5x =15
二元一次方程
y =0.5x+15
用方程观点看
用函数观点看
从式子(数)角度看:
由函数图象的定义可知:
直线y =0.5x+15上的每个点的坐标(x,y)都能使等式y=0.5x+15成立,即直线y =0.5x+15上的每个点的坐标都是二元一次方程y=0.5x+15的解
思考2:从形的角度看,一次函数与二元一次方程有什么关系?
15
10
5
-5
5
10
O
x
y
y =0.5x+15
一次函数与二元一次方程的关系
由于任意一个二元一次方程都可以转化为y=kx+b的
形式,因此有:
(1)二元一次方程 一次函数 一条直线;
(2)二元一次方程的解 一次函数两变量的值 直
线上的点的坐标.
对应
对应
即为
即为
从数的角度看:
就是求自变量为何值时,两个一次函数 y =x+5,y =0.5x+15 的函数值相等,并求出函数值.
解方程组
y =x+5
y =0.5x+15
h1
h2
(2)什么时刻,1 号气球的高度赶上2 号气球的高度?这时的高度是多少?请从数和形两方面分别加以研究.
气球1 海拔高度:y =x+5
气球2 海拔高度:y =0.5x+15
二元一次方程
组的解就是相应的
两个一次函数图象
的交点坐标.
A(20,25)
30
25
20
15
10
5
10
20
y =x+5
y =0.5x+15
15
5
O
x
y
从形的角度看,二元一次方程组与一次函数有什么关系?
1. 一次函数与二元一次方程组:
(1)二元一次方程组与一次函数的对应关系:
二元一次方程组 两个一次函数 两条直线;
二元一次方程组的解 两个一次函数值相等时的自变量值及函数值 两条直线的交点坐标.
(2)两直线交点个数与二元一次方程组解的个数的关系:
两条直线有交点(相交)?方程组只有一个解;
两条直线无交点(平行)?方程组无解;
两条直线是同一直线(重合)?方程组有无数个解.
对应
对应
即为
即为
总结
(3)用一次函数图象法解二元一次方程组的步骤:
①将方程组中每个方程分别转化成一次函数表达式;
②在同一坐标系中分别画出转化后的两个一次函数
的图象;
③根据两个函数图象的交点坐标写出方程组的解.
2. 易错警示:
对两直线交点与二元一次方程组的解的理解不透彻
而出错.
如图所示的四条直线,其中直线上每个点的坐标都是二元一次方程x-2y=2的解的是( )
例1
C
如图,一次函数y=ax+b与y=cx+d的图象交于点P,则方程组 的解是多少?
解:此方程组的解是
1
2
3
-1
-2
-3
-1
-3
-4
-5
2
O
-2
1
4
-6
x
y
P
y=ax+b
y=cx+d
例2
如图,在平面直角坐标系xOy中,
已知正比例函数y= x与一次函
数y=-x+7的图象交于点A.
(1)求点A的坐标;
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位
于点A的右侧),分别交y= x和y=-x+7的图象于
点B,C,连接OC,若BC=7,求△OBC的面积.
例3
(1)由题意得 解得
所以点A的坐标为(4,3).
(2)因为P(a,0),所以B ,
C(a,-a+7),
所以BC= a-(-a+7)= a-7,
所以 a-7=7,解得a=8.
所以S三角形OBC= BC·OP= ×7×8=28.
解:
已知一次函数y=ax+2与y=kx+b的
图象如图,且方程组
的解为 点B的坐标为(0,-1),
请你确定这两个一次函数的表达式.
例4
∵方程组 的解为
∴交点A的坐标为(2,1),
∴2a+2=1,解得a=- .
又∵函数y=kx+b的图象过交点A(2,1)和点B(0,-1)
∴ 解得
∴这两个一次函数的表达式分别为y=- x+2, y=x-1.
解:
1、直线y=kx+b(k≠0)对应的表达式就是一个关于x,
y的__________方程;以关于x,y的二元一次方程
y-kx=b(k≠0)的解为坐标的点组成的图象就是一
次函数______________的图象.
二元一次
y=kx+b(k≠0)
课堂练习
2、以下四条直线,其中直线上每个点的坐标都是二元一次方程x-2y=2的解的是( )
A B C D
C
3、已知 的解为 则直线
y=ax+b与y=-cx+d的交点坐标为( )
A.(1,2) B.(-1,2)
C.(1,-2) D.(-1,-2)
A
4、在平面直角坐标系中,点A,B的坐标分别为
(m,3),(3m-1,3),若线段AB与直线y=2x+1相交,则m的取值范围为___________.
1.一次函数与二元一次方程之间的区别和联系:
区别:(1)二元一次方程有两个未知数,而一次函数有两个变量;
(2)二元一次方程是用一个等式表示两个未知数的关系,而一次函数既可以用一个等式表示两个变量之间的关系,又可以用表格或图象来表示两个变量之间的关系.
联系:在直角坐标系中分别描出以二元一次方程的解为坐标的点,这些点都在相应的一次函数的图象上.
2. 求两直线的交点坐标方法是:联立两直线的解析式组成方程组,方程组的解就是交点的纵横坐标. 当两直线平行时,k相等,且方程组无解.
