2020-2021学年华东师大版八年级下册 17.3.3 一次函数的性质课件(20张ppt)
文档属性
| 名称 | 2020-2021学年华东师大版八年级下册 17.3.3 一次函数的性质课件(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 198.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 09:05:30 | ||
图片预览




文档简介
第17章 函数及其图象
17.3 一次函数
第3课时 一次函数的
性质
复习引入
1.一次函数图象有什么特点?
2.作出一次函数图象需要描出几个点?
只需要描出2个点.
一次函数y=kx+b的图象是一条直线,直线上所有点的坐标都满足表达式y=kx+b.
一般选直线与两坐标轴的两交点,即(0,b)和( ,0).
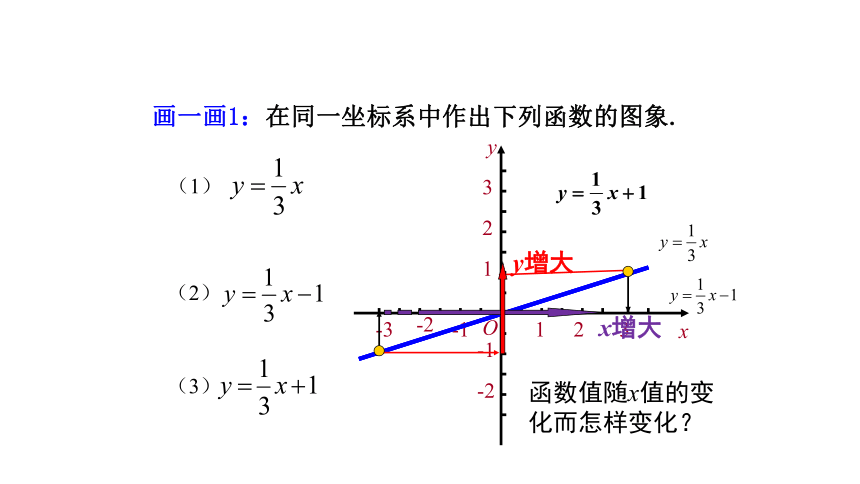
画一画1:在同一坐标系中作出下列函数的图象.
(1)
(2)
(3)
-3
O
-2
2
3
1
2
3
-1
-1
-2
x
y
1
函数值随x值的变化而怎样变化?
x增大
y增大
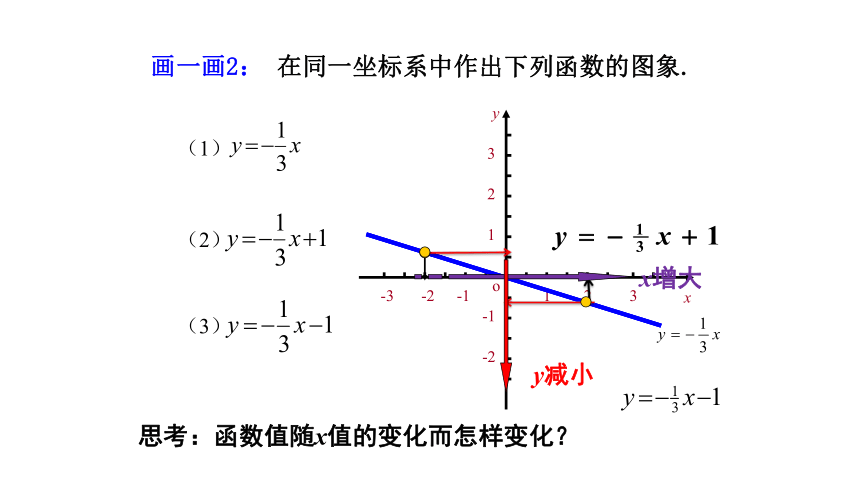
画一画2: 在同一坐标系中作出下列函数的图象.
(1)
(2)
(3)
-3
o
-2
2
3
1
2
3
-1
-1
-2
x
y
1
思考:函数值随x值的变化而怎样变化?
x增大
y减小
在一次函数y=kx+b中,
当k>0时,直线自左向右上升,y的值随着x值的增大而增大;
当k<0时,直线自左向右下降,y的值随着x值的增大而减小.
由此得到一次函数性质:
例1、若点(-1,a),(3,b)都在函数y=x+2的图象上,则a与b的大小关系是( )
A.a>b B.a<b
C.a=b D.无法确定
B
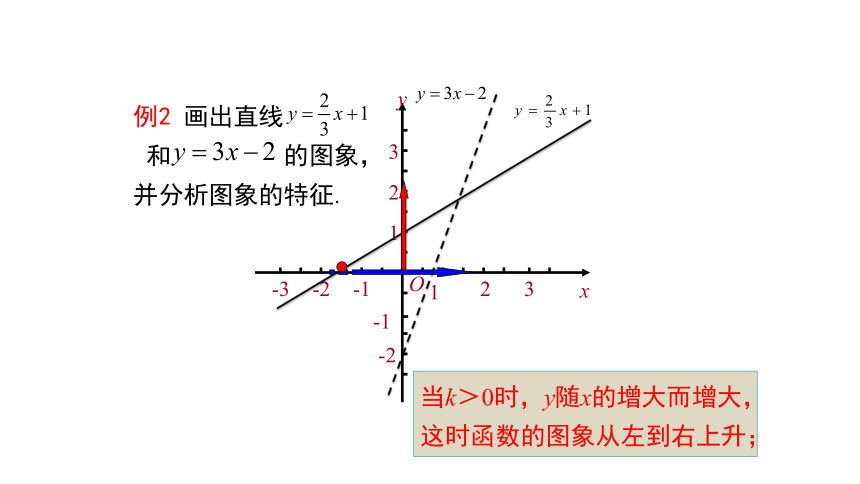
例2 画出直线
和 的图象,
并分析图象的特征.
-3
O
-2
2
3
1
2
3
-1
-1
-2
x
1
y
当k>0时,y随x的增大而增大,
这时函数的图象从左到右上升;
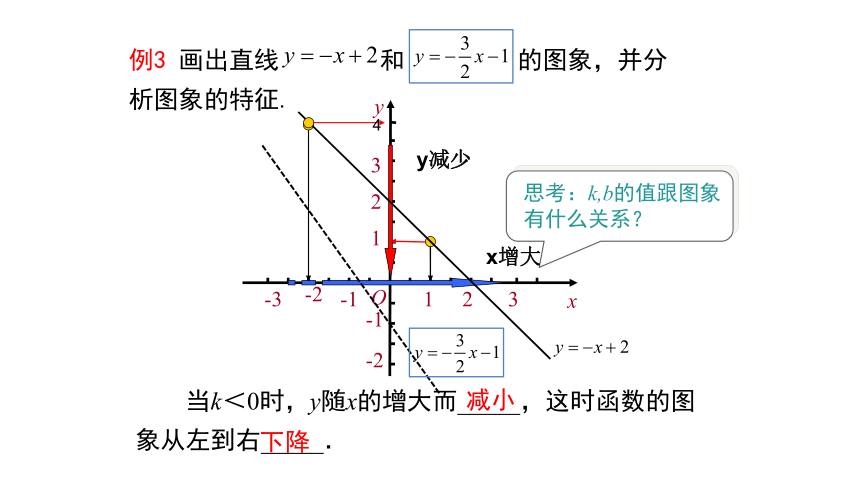
当k<0时,y随x的增大而_____,这时函数的图象从左到右_____.
-3
O
-2
2
3
1
2
3
-1
-1
-2
x
y
1
4
y减少
x增大
减小
下降
例3 画出直线 和 的图象,并分析图象的特征.
思考:k,b的值跟图象
有什么关系?
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
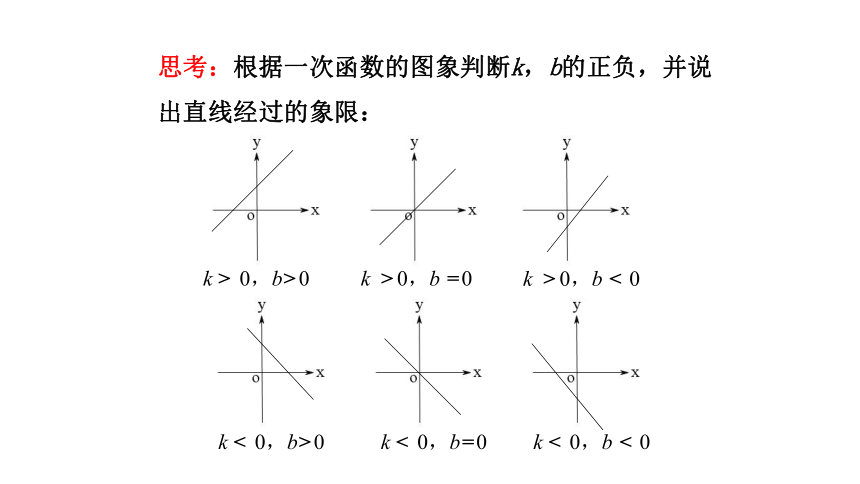
思考:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
归纳总结
一次函数y=kx+b中,k,b的正负对函数图象及性质有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
① b>0时,直线经过 第一、二、四象限;
② b<0时,直线经过第二、三、四象限.
① b>0时,直线经过第一、二、三象限;
② b<0时,直线经过第一、三、四象限.
例4 已知关于x的一次函数y=(2k-1)x+(2k+1).
(1)当k满足什么条件时,函数y的值随x的值的增大而增大?
(2)当k满足什么条件时,y=(2k-1)x+(2k+1)的图象经过原点?
当2k-1>0时,y的值随x的值增大而增大.
解2k-1>0,得k>0.5.
当2k+1=0,即k=-0.5时,
函数y=(2k-1)x+(2k+1)的图象经过原点.
(3)当k满足什么条件时,函数y=(2k-1)x+(2k+1)的图象与y轴的交点在x轴的下方?
(4)当k满足什么条件时,函数y的值随x的值的增大而减小且函数图象与y轴的交点在x轴的上方?
当2k+1<0,函数y=(2k-1)x+(2k+1)的图象与y轴的交点在x轴的下方.解2k+1<0,得k<-0.5.
当2k-1<0时,y的值随x的值的增大而减小.解得k <0.5.
当2k+1> 0,函数y=(2k-1)x+(2k+1)的图象与y轴的交点在x轴的上方.解得k> -0.5.
所以此时k的取值范围为-0.5<k <0.5.
总 结
对于一次函数y=kx+b,(1)判断k值符号的方法:
①增减性法:当y随x的增大而增大时,k>0;反之,k<0.
②直线升、降法:当直线从左到右上升时,k>0;反之,k<0.
③经过象限法:直线过第一、三象限时,k>0;直线过第二、四象限时,k<0.
(2)判断b值符号的方法:
与y轴交点法,即若直线y=kx+b与y轴交于正半轴,则b>0;与y轴交于负半轴,则b<0;与y轴交于原点,则b=0.
如果一次函数y=kx+b的图象不经过第二象限,
也不经过原点,那么k,b的取值范围是( )
A.k>0且b>0 B.k>0且b<0
C.k<0且b<0 D.k<0且b>0
1
下列函数中,其图象同时满足下面两个条件的是( )
①y随着x的增大而增大;②与x轴的正半轴相交.
A.y=-2x-1 B.y=-2x+1
C.y=2x-1 D.y=2x+1
2
B
C
课堂练习
已知点A(-2,y1)和点B(1,y2)是如图所示的一次函数
y=2x+b图象上的两点,则y1与y2的大小关系是( )
A.y1B.y1>y2
C.y1=y2
D.y1≥y2
3
A
一次函数y=kx-k(k<0)的大致图象是( )
4
A
已知一次函数y=mx+n-2的图象如图所示,则
m,n的取值范围是( )
A.m>0,n<2
B.m>0,n>2
C.m<0,n<2
D.m<0,n>2
5
D
已知一次函数y=(6+3m)x+(m-4),y随x的增大而
增大,函数的图象与y轴的交点在y轴的负半轴上,
求m的取值范围.
6
根据一次函数的性质可知,6+3m>0,且m-4<0,
解不等式组即可.
导引:
根据题意,得 解得-2<m<4.
所以m的取值范围是-2<m<4.
解:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
一次函数
概 念
一般地,形如y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数.当b=0时,是y=kx,所以说正比例函数是一种特殊的一次函数.
自变量范围
x为全体实数
必过点
(0,b)和(- ,0)?
走 向
k>0,b>0,直线经过第一、二、三象限
k>0,b<0直线经过第一、三、四象限
k<0,b>0直线经过第一、二、四象限
k<0,b<0直线经过第二、三、四象限?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
一次函数
图 象
一条直线
增减性
k>0,y随x的增大而增大;(从左向右上升)
k<0,y随x的增大而减小。(从左向右下降)
倾斜度
|k|越大,越接近y轴;|k|越小,越接近x轴
图像的平移
b>0时,将直线y=kx的图象向上平移 |b|个单位;
b<0时,将直线y=kx的图象向下平移 |b|个单位.
17.3 一次函数
第3课时 一次函数的
性质
复习引入
1.一次函数图象有什么特点?
2.作出一次函数图象需要描出几个点?
只需要描出2个点.
一次函数y=kx+b的图象是一条直线,直线上所有点的坐标都满足表达式y=kx+b.
一般选直线与两坐标轴的两交点,即(0,b)和( ,0).
画一画1:在同一坐标系中作出下列函数的图象.
(1)
(2)
(3)
-3
O
-2
2
3
1
2
3
-1
-1
-2
x
y
1
函数值随x值的变化而怎样变化?
x增大
y增大
画一画2: 在同一坐标系中作出下列函数的图象.
(1)
(2)
(3)
-3
o
-2
2
3
1
2
3
-1
-1
-2
x
y
1
思考:函数值随x值的变化而怎样变化?
x增大
y减小
在一次函数y=kx+b中,
当k>0时,直线自左向右上升,y的值随着x值的增大而增大;
当k<0时,直线自左向右下降,y的值随着x值的增大而减小.
由此得到一次函数性质:
例1、若点(-1,a),(3,b)都在函数y=x+2的图象上,则a与b的大小关系是( )
A.a>b B.a<b
C.a=b D.无法确定
B
例2 画出直线
和 的图象,
并分析图象的特征.
-3
O
-2
2
3
1
2
3
-1
-1
-2
x
1
y
当k>0时,y随x的增大而增大,
这时函数的图象从左到右上升;
当k<0时,y随x的增大而_____,这时函数的图象从左到右_____.
-3
O
-2
2
3
1
2
3
-1
-1
-2
x
y
1
4
y减少
x增大
减小
下降
例3 画出直线 和 的图象,并分析图象的特征.
思考:k,b的值跟图象
有什么关系?
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
思考:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
归纳总结
一次函数y=kx+b中,k,b的正负对函数图象及性质有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
① b>0时,直线经过 第一、二、四象限;
② b<0时,直线经过第二、三、四象限.
① b>0时,直线经过第一、二、三象限;
② b<0时,直线经过第一、三、四象限.
例4 已知关于x的一次函数y=(2k-1)x+(2k+1).
(1)当k满足什么条件时,函数y的值随x的值的增大而增大?
(2)当k满足什么条件时,y=(2k-1)x+(2k+1)的图象经过原点?
当2k-1>0时,y的值随x的值增大而增大.
解2k-1>0,得k>0.5.
当2k+1=0,即k=-0.5时,
函数y=(2k-1)x+(2k+1)的图象经过原点.
(3)当k满足什么条件时,函数y=(2k-1)x+(2k+1)的图象与y轴的交点在x轴的下方?
(4)当k满足什么条件时,函数y的值随x的值的增大而减小且函数图象与y轴的交点在x轴的上方?
当2k+1<0,函数y=(2k-1)x+(2k+1)的图象与y轴的交点在x轴的下方.解2k+1<0,得k<-0.5.
当2k-1<0时,y的值随x的值的增大而减小.解得k <0.5.
当2k+1> 0,函数y=(2k-1)x+(2k+1)的图象与y轴的交点在x轴的上方.解得k> -0.5.
所以此时k的取值范围为-0.5<k <0.5.
总 结
对于一次函数y=kx+b,(1)判断k值符号的方法:
①增减性法:当y随x的增大而增大时,k>0;反之,k<0.
②直线升、降法:当直线从左到右上升时,k>0;反之,k<0.
③经过象限法:直线过第一、三象限时,k>0;直线过第二、四象限时,k<0.
(2)判断b值符号的方法:
与y轴交点法,即若直线y=kx+b与y轴交于正半轴,则b>0;与y轴交于负半轴,则b<0;与y轴交于原点,则b=0.
如果一次函数y=kx+b的图象不经过第二象限,
也不经过原点,那么k,b的取值范围是( )
A.k>0且b>0 B.k>0且b<0
C.k<0且b<0 D.k<0且b>0
1
下列函数中,其图象同时满足下面两个条件的是( )
①y随着x的增大而增大;②与x轴的正半轴相交.
A.y=-2x-1 B.y=-2x+1
C.y=2x-1 D.y=2x+1
2
B
C
课堂练习
已知点A(-2,y1)和点B(1,y2)是如图所示的一次函数
y=2x+b图象上的两点,则y1与y2的大小关系是( )
A.y1
C.y1=y2
D.y1≥y2
3
A
一次函数y=kx-k(k<0)的大致图象是( )
4
A
已知一次函数y=mx+n-2的图象如图所示,则
m,n的取值范围是( )
A.m>0,n<2
B.m>0,n>2
C.m<0,n<2
D.m<0,n>2
5
D
已知一次函数y=(6+3m)x+(m-4),y随x的增大而
增大,函数的图象与y轴的交点在y轴的负半轴上,
求m的取值范围.
6
根据一次函数的性质可知,6+3m>0,且m-4<0,
解不等式组即可.
导引:
根据题意,得 解得-2<m<4.
所以m的取值范围是-2<m<4.
解:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
一次函数
概 念
一般地,形如y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数.当b=0时,是y=kx,所以说正比例函数是一种特殊的一次函数.
自变量范围
x为全体实数
必过点
(0,b)和(- ,0)?
走 向
k>0,b>0,直线经过第一、二、三象限
k>0,b<0直线经过第一、三、四象限
k<0,b>0直线经过第一、二、四象限
k<0,b<0直线经过第二、三、四象限?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
一次函数
图 象
一条直线
增减性
k>0,y随x的增大而增大;(从左向右上升)
k<0,y随x的增大而减小。(从左向右下降)
倾斜度
|k|越大,越接近y轴;|k|越小,越接近x轴
图像的平移
b>0时,将直线y=kx的图象向上平移 |b|个单位;
b<0时,将直线y=kx的图象向下平移 |b|个单位.
