2020-2021学年华东师大版八年级下册 第18章 平行四边形 小结与复习课件(16张ppt)
文档属性
| 名称 | 2020-2021学年华东师大版八年级下册 第18章 平行四边形 小结与复习课件(16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 428.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 09:20:49 | ||
图片预览


文档简介
小结与复习
第18章 平行四边形
几 何 语 言
文字叙述
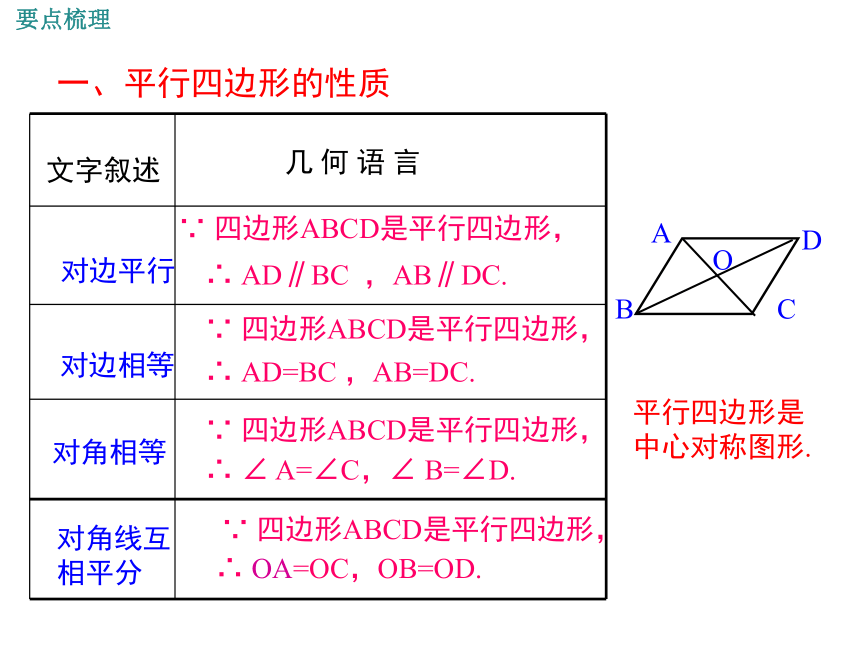
对边平行
对边相等
对角相等
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
一、平行四边形的性质
要点梳理
对角线互
相平分
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
平行四边形是
中心对称图形.
A
B
C
D
O
几 何 语 言
文字叙述
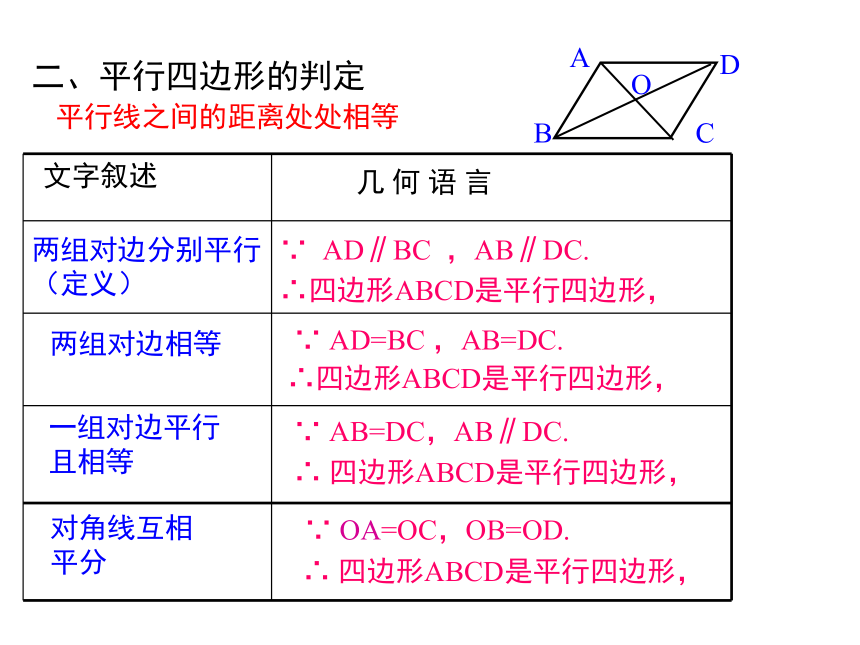
两组对边相等
一组对边平行且相等
∴四边形ABCD是平行四边形,
∵ AD=BC ,AB=DC.
∴ 四边形ABCD是平行四边形,
∵ AB=DC,AB∥DC.
二、平行四边形的判定
对角线互相平分
∴ 四边形ABCD是平行四边形,
∵ OA=OC,OB=OD.
两组对边分别平行(定义)
∴四边形ABCD是平行四边形,
∵ AD∥BC ,AB∥DC.
平行线之间的距离处处相等
A
B
C
D
O
C
D
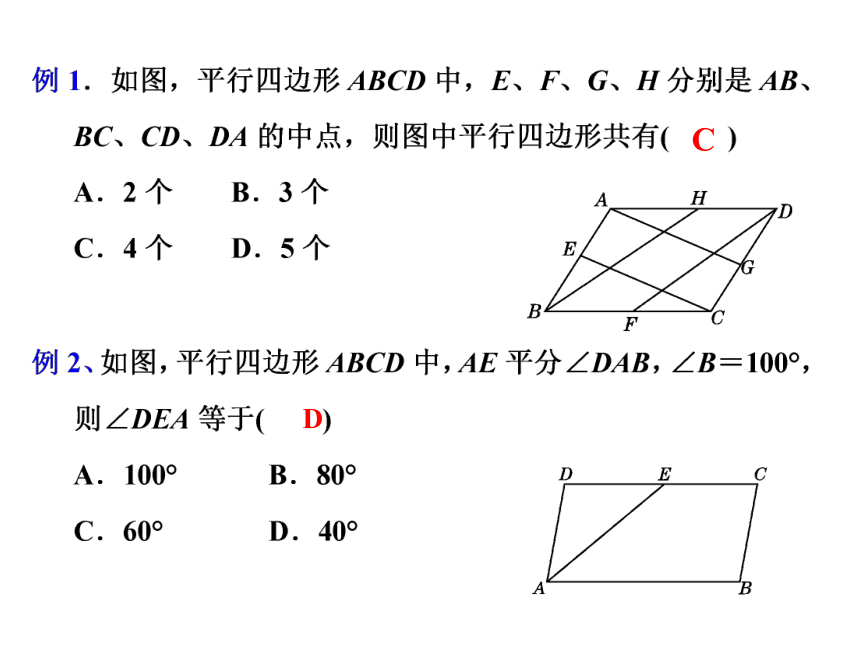
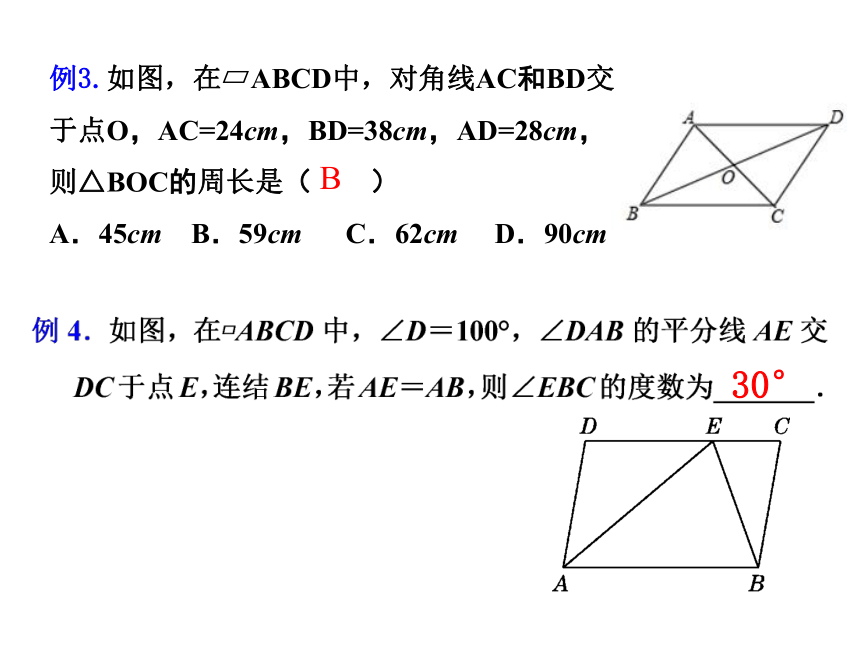
例3.如图,在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
A.45cm B.59cm C.62cm D.90cm
B
30°
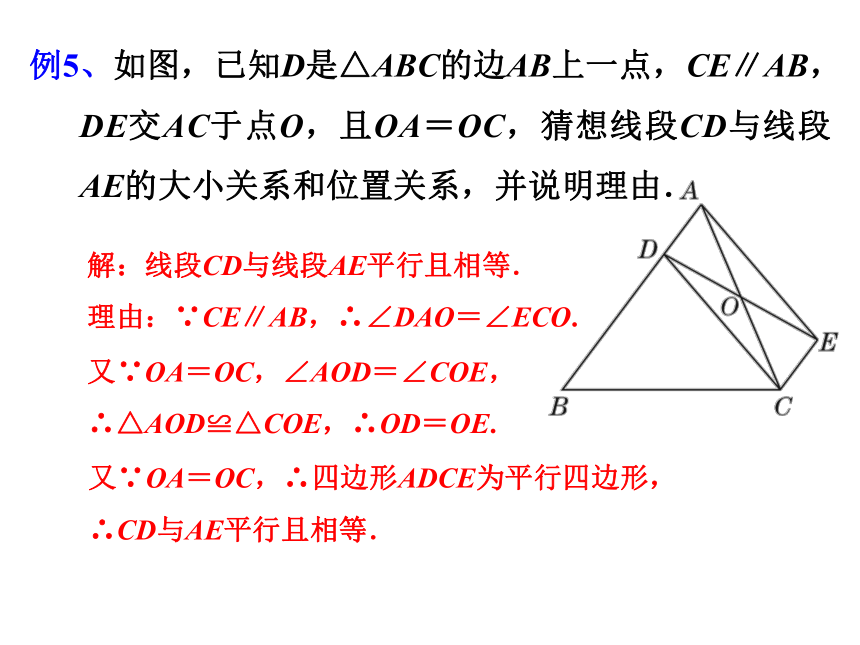
例5、如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并说明理由.
解:线段CD与线段AE平行且相等.
理由:∵CE∥AB,∴∠DAO=∠ECO.
又∵OA=OC,∠AOD=∠COE,
∴△AOD≌△COE,∴OD=OE.
又∵OA=OC,∴四边形ADCE为平行四边形,
∴CD与AE平行且相等.
例7、如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC
D.AB=CD,AO=CO
D
例8.如图,已知BE∥DF,∠ADF=∠CBE,AF=CE.求证:四边形DEBF是平行四边形.
证明:∵BE∥DF,∴∠AFD=∠CEB.
又∵∠ADF=∠CBE,AF=CE,
∴△ADF≌△CBE(A.A.S.).∴DF=BE.
又∵BE∥DF,
∴四边形DEBF是平行四边形.
例9、如图,点D、C在BF上,AC∥DE,∠A=∠E,BD=CF,
(1)求证:AB=EF.
(2)连接AF,BE,猜想四边形ABEF的形状,并说明理由.
(1)证明:∵AC∥DE, ∴∠ACD=∠EDF,
∵BD=CF,∴BD+DC=CF+DC, 即BC=DF,
又∵∠A=∠E,∴△ABC≌△EFD(AAS),
∴AB=EF;
(2)猜想:四边形ABEF为平行四边形,
理由如下:由(1)知△ABC≌△EFD,
∴∠B=∠F,∴AB∥EF,
又∵AB=EF,
四边形ABEF为平行四边形
变式1、如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC=BC
D
14
变式3、如图,已知?ABCD中,AE平分∠BAD,CF平分
∠BCD,分别交BC、AD于E、F.求证:AF=EC.
证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AD=BC,AB=CD,∠BAD=∠BCD,
∵AE平分∠BAD,CF平分∠BCD,
∴∠EAB= ∠BAD,∠FCD= ∠BCD,∴∠EAB= ∠FCD,
在△ABE和△CDF中
∠B=∠D
AB=CD ∴△ABE≌△CDF,∴BE=DF.
∠EAB=∠FCD
∵AD=BC ∴AF=EC.
变式4、如图,在?ABCD中,点E,F在对角线BD上,且BE=DF.
求证:(1)AE=CF;
(2)四边形AECF是平行四边形.
证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD.∴∠ABE=∠CDF.
(2),连结AC,与BD交于点O.
∵四边形ABCD为平行四边形,
∴AO=CO,BO=DO.
又∵BE=DF,∴EO=FO.
∴四边形AECF是平行四边形.
平 行 四 边 形
性质
①对边平行且相等
②对角相等,邻角互补
③对角线互相平分
判定
①两组对边分别平行的
②两组对边分别相等的
③一组对边平行且相等的
④对角线互相平分的
四 边 形
平 行 四 边 形
课堂小结
第18章 平行四边形
几 何 语 言
文字叙述
对边平行
对边相等
对角相等
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
一、平行四边形的性质
要点梳理
对角线互
相平分
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
平行四边形是
中心对称图形.
A
B
C
D
O
几 何 语 言
文字叙述
两组对边相等
一组对边平行且相等
∴四边形ABCD是平行四边形,
∵ AD=BC ,AB=DC.
∴ 四边形ABCD是平行四边形,
∵ AB=DC,AB∥DC.
二、平行四边形的判定
对角线互相平分
∴ 四边形ABCD是平行四边形,
∵ OA=OC,OB=OD.
两组对边分别平行(定义)
∴四边形ABCD是平行四边形,
∵ AD∥BC ,AB∥DC.
平行线之间的距离处处相等
A
B
C
D
O
C
D
例3.如图,在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
A.45cm B.59cm C.62cm D.90cm
B
30°
例5、如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并说明理由.
解:线段CD与线段AE平行且相等.
理由:∵CE∥AB,∴∠DAO=∠ECO.
又∵OA=OC,∠AOD=∠COE,
∴△AOD≌△COE,∴OD=OE.
又∵OA=OC,∴四边形ADCE为平行四边形,
∴CD与AE平行且相等.
例7、如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC
D.AB=CD,AO=CO
D
例8.如图,已知BE∥DF,∠ADF=∠CBE,AF=CE.求证:四边形DEBF是平行四边形.
证明:∵BE∥DF,∴∠AFD=∠CEB.
又∵∠ADF=∠CBE,AF=CE,
∴△ADF≌△CBE(A.A.S.).∴DF=BE.
又∵BE∥DF,
∴四边形DEBF是平行四边形.
例9、如图,点D、C在BF上,AC∥DE,∠A=∠E,BD=CF,
(1)求证:AB=EF.
(2)连接AF,BE,猜想四边形ABEF的形状,并说明理由.
(1)证明:∵AC∥DE, ∴∠ACD=∠EDF,
∵BD=CF,∴BD+DC=CF+DC, 即BC=DF,
又∵∠A=∠E,∴△ABC≌△EFD(AAS),
∴AB=EF;
(2)猜想:四边形ABEF为平行四边形,
理由如下:由(1)知△ABC≌△EFD,
∴∠B=∠F,∴AB∥EF,
又∵AB=EF,
四边形ABEF为平行四边形
变式1、如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC=BC
D
14
变式3、如图,已知?ABCD中,AE平分∠BAD,CF平分
∠BCD,分别交BC、AD于E、F.求证:AF=EC.
证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AD=BC,AB=CD,∠BAD=∠BCD,
∵AE平分∠BAD,CF平分∠BCD,
∴∠EAB= ∠BAD,∠FCD= ∠BCD,∴∠EAB= ∠FCD,
在△ABE和△CDF中
∠B=∠D
AB=CD ∴△ABE≌△CDF,∴BE=DF.
∠EAB=∠FCD
∵AD=BC ∴AF=EC.
变式4、如图,在?ABCD中,点E,F在对角线BD上,且BE=DF.
求证:(1)AE=CF;
(2)四边形AECF是平行四边形.
证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD.∴∠ABE=∠CDF.
(2),连结AC,与BD交于点O.
∵四边形ABCD为平行四边形,
∴AO=CO,BO=DO.
又∵BE=DF,∴EO=FO.
∴四边形AECF是平行四边形.
平 行 四 边 形
性质
①对边平行且相等
②对角相等,邻角互补
③对角线互相平分
判定
①两组对边分别平行的
②两组对边分别相等的
③一组对边平行且相等的
④对角线互相平分的
四 边 形
平 行 四 边 形
课堂小结
