2020-2021学年华东师大版八年级下册18.2.1 由边的关系判定平行四边形课件(共15张)
文档属性
| 名称 | 2020-2021学年华东师大版八年级下册18.2.1 由边的关系判定平行四边形课件(共15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 134.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 10:56:46 | ||
图片预览






文档简介
第1课时 由边的关系判定
平行四边形
第18章 平行四边形
18.2 平行四边形的判定
我们已经知道,如果一个四边形是平行四边形,
那么它的两组对边分别平行,且是一个中心对称图
形,具有如 下一些性质:
1. 两组对边分别相等;
2. 两组对角分别相等;
3. 两条对角线互相平分.
那么,怎样判定一个四边形是否是平行四边形呢?
判定方法:
(1)从边看:
方法一:两组对边分别平行的四边形是平行四边
形;(定义法)
数学表达式:
如图,∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
猜想 :将两长两短的四根细木条用小钉固定在一起,任意拉动,所得的四边形是平行四边形吗?
由两组对边的关系判定平行四边形
你能根据平行四边形的定义证明它们吗?
已知: 四边形ABCD中,AB=DC,AD=BC.
求证: 四边形ABCD是平行四边形.
A
B
C
D
连接AC,
在△ABC和△CDA中,
AB=CD (已知),
BC=DA(已知),
AC=CA (公共边),
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3,
∴AB∥ CD , AD∥ BC,
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
证一证
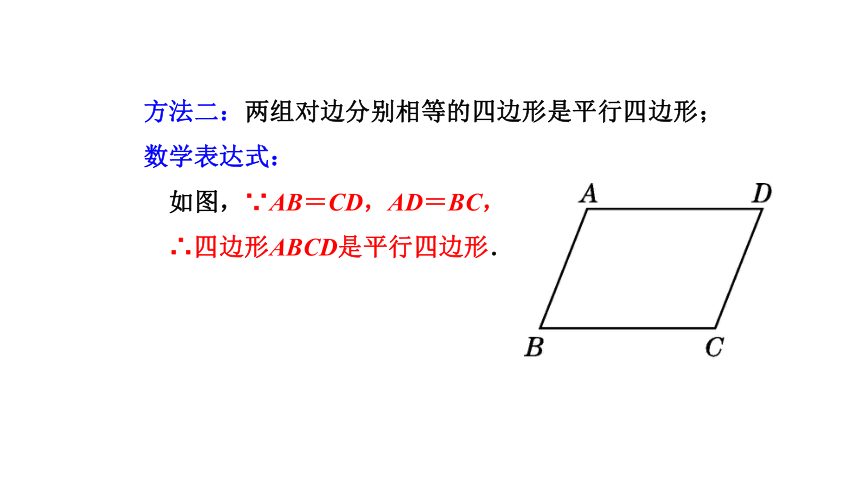
方法二:两组对边分别相等的四边形是平行四边形;
数学表达式:
如图,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
例1、如图, AD⊥AC,BC⊥AC,且AB=CD,
求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△CDA中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=AD.
又∵AB=CD,
∴四边形ABCD是平行四边形.
例2
如图,已知四边形ABCD是平行四边形,DE平分∠ADC,交CB的延长线于点E,BF平分∠ABC,交AD的延长线于点F. 求证:四边形BFDE是平行四边形.
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD∥CB. ∴DF∥BE.
∵DE平分∠ADC,BF平分∠ABC,
∴∠1=∠2=∠3=∠4.
∵AD∥BC,∴∠1=∠E. ∴∠E=∠3.
∴DE∥FB.
∴四边形BFDE是平行四边形(两组对边分别平行的四边形是平行四边形).
证明:
问题 我们知道,两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
猜想1:一组对边相等的四边形是平行四边形.
等腰梯形不是平行四边形,因而此猜想错误.
猜想2:一组对边平行的四边形是平行四边形.
梯形的上下底平行,但不是平行四边形,因而此猜想错误.
由一组对边的关系判定平行四边形
B
A
活动 如图,将线段AB向右平移BC长度后得到线段DC,连接AD,BC,由此你能猜想四边形ABCD的形状吗?
D
C
四边形ABCD是平行四边形
猜想3:一组对边平行且相等的四边形是平行四边形.
你能证明吗?
A
B
C
D
如图,在四边形ABCD中,AB=CD且AB∥CD,
求证:四边形ABCD是平行四边形.
证一证
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
AB=CD,
AC=CA,
∠1=∠2,
∴△ABC≌△CDA(SAS),
∴BC=DA .
又∵AB= CD,
2
1
方法三:一组对边平行且相等的四边形是平行四边形;
数学表达式:
如图,∵AB CD,
∴四边形ABCD是平行四边形.
证明:
∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
例3 如图 ,在平 ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.
如图,在 ABCD中,点E,F分别为AB,CD上的点,且AE=CF,点M,N分别是BF,DE的中点.
求证:四边形ENFM是平行四边形.
例4
∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB.
又∵CF=AE,∴CD-CF=AB-AE,即DF=EB.
∴四边形DEBF是平行四边形. ∴DE∥BF,DE=BF.
又∵点M,N分别为BF,DE的中点,
∴FM= BF,NE= DE. ∴NE=FM.
∴四边形ENFM为平行四边形(一组对边平行且相等的四边形是平行四边形).
证明:
与边有关的判定平行四边形的方法:
1.两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
平行四边形
第18章 平行四边形
18.2 平行四边形的判定
我们已经知道,如果一个四边形是平行四边形,
那么它的两组对边分别平行,且是一个中心对称图
形,具有如 下一些性质:
1. 两组对边分别相等;
2. 两组对角分别相等;
3. 两条对角线互相平分.
那么,怎样判定一个四边形是否是平行四边形呢?
判定方法:
(1)从边看:
方法一:两组对边分别平行的四边形是平行四边
形;(定义法)
数学表达式:
如图,∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
猜想 :将两长两短的四根细木条用小钉固定在一起,任意拉动,所得的四边形是平行四边形吗?
由两组对边的关系判定平行四边形
你能根据平行四边形的定义证明它们吗?
已知: 四边形ABCD中,AB=DC,AD=BC.
求证: 四边形ABCD是平行四边形.
A
B
C
D
连接AC,
在△ABC和△CDA中,
AB=CD (已知),
BC=DA(已知),
AC=CA (公共边),
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3,
∴AB∥ CD , AD∥ BC,
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
证一证
方法二:两组对边分别相等的四边形是平行四边形;
数学表达式:
如图,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
例1、如图, AD⊥AC,BC⊥AC,且AB=CD,
求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△CDA中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=AD.
又∵AB=CD,
∴四边形ABCD是平行四边形.
例2
如图,已知四边形ABCD是平行四边形,DE平分∠ADC,交CB的延长线于点E,BF平分∠ABC,交AD的延长线于点F. 求证:四边形BFDE是平行四边形.
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD∥CB. ∴DF∥BE.
∵DE平分∠ADC,BF平分∠ABC,
∴∠1=∠2=∠3=∠4.
∵AD∥BC,∴∠1=∠E. ∴∠E=∠3.
∴DE∥FB.
∴四边形BFDE是平行四边形(两组对边分别平行的四边形是平行四边形).
证明:
问题 我们知道,两组对边分别平行或相等的四边形是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
猜想1:一组对边相等的四边形是平行四边形.
等腰梯形不是平行四边形,因而此猜想错误.
猜想2:一组对边平行的四边形是平行四边形.
梯形的上下底平行,但不是平行四边形,因而此猜想错误.
由一组对边的关系判定平行四边形
B
A
活动 如图,将线段AB向右平移BC长度后得到线段DC,连接AD,BC,由此你能猜想四边形ABCD的形状吗?
D
C
四边形ABCD是平行四边形
猜想3:一组对边平行且相等的四边形是平行四边形.
你能证明吗?
A
B
C
D
如图,在四边形ABCD中,AB=CD且AB∥CD,
求证:四边形ABCD是平行四边形.
证一证
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
AB=CD,
AC=CA,
∠1=∠2,
∴△ABC≌△CDA(SAS),
∴BC=DA .
又∵AB= CD,
2
1
方法三:一组对边平行且相等的四边形是平行四边形;
数学表达式:
如图,∵AB CD,
∴四边形ABCD是平行四边形.
证明:
∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
例3 如图 ,在平 ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.
如图,在 ABCD中,点E,F分别为AB,CD上的点,且AE=CF,点M,N分别是BF,DE的中点.
求证:四边形ENFM是平行四边形.
例4
∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB.
又∵CF=AE,∴CD-CF=AB-AE,即DF=EB.
∴四边形DEBF是平行四边形. ∴DE∥BF,DE=BF.
又∵点M,N分别为BF,DE的中点,
∴FM= BF,NE= DE. ∴NE=FM.
∴四边形ENFM为平行四边形(一组对边平行且相等的四边形是平行四边形).
证明:
与边有关的判定平行四边形的方法:
1.两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
